Inputting the Hamilton data, table 4.1, p. 9
data p095; input Y X1 X2; cards; 12.37 2.23 9.66 12.66 2.57 8.94 12 3.87 4.4 11.93 3.1 6.64 11.06 3.39 4.91 13.03 2.83 8.52 13.13 3.02 8.04 11.44 2.14 9.05 12.86 3.04 7.71 10.84 3.26 5.11 11.2 3.39 5.05 11.56 2.35 8.51 10.83 2.76 6.59 12.63 3.9 4.9 12.46 3.16 6.96 ; run;
Correlations and scatter matrix, p. 94
Invoking a macro in order to create a scatter plot matrix.
proc corr data = p095; var y x1 x2; run; %scatter(data=p095, y x1 x2);
The CORR Procedure
3 Variables: Y X1 X2
Simple Statistics
Variable N Mean Std Dev Sum Minimum Maximum
Y 15 12.00000 0.80217 180.00000 10.83000 13.13000
X1 15 3.00067 0.53470 45.01000 2.14000 3.90000
X2 15 6.99933 1.78145 104.99000 4.40000 9.66000
Pearson Correlation Coefficients, N = 15
Prob > |r| under H0: Rho=0
Y X1 X2
Y 1.00000 0.00250 0.43407
0.9930 0.1060
X1 0.00250 1.00000 -0.89978
0.9930 <.0001
X2 0.43407 -0.89978 1.00000
0.1060 <.0001
Fitted Equations, p. 95.
proc reg data = p095; model y = x1; model y = x2; model y=x1 x2; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: YAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F Model 1 0.00005621 0.00005621 0.00 0.9930 Error 13 9.00854 0.69296 Corrected Total 14 9.00860
Root MSE 0.83245 R-Square 0.0000 Dependent Mean 12.00000 Adj R-Sq -0.0769 Coeff Var 6.93704 Parameter Estimates
Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 11.98876 1.26689 9.46 <.0001 X1 1 0.00375 0.41608 0.01 0.9930
The REG Procedure Model: MODEL2 Dependent Variable: Y
Analysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F Model 1 1.69736 1.69736 3.02 0.1060 Error 13 7.31124 0.56240 Corrected Total 14 9.00860
Root MSE 0.74994 R-Square 0.1884 Dependent Mean 12.00000 Adj R-Sq 0.1260 Coeff Var 6.24946
Parameter Estimates
Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 10.63194 0.81094 13.11 <.0001 X2 1 0.19546 0.11251 1.74 0.1060
The REG Procedure Model: MODEL3 Dependent Variable: Y
Analysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F Model 2 9.00722 4.50361 39222.3 <.0001 Error 12 0.00138 0.00011482 Corrected Total 14 9.00860
Root MSE 0.01072 R-Square 0.9998 Dependent Mean 12.00000 Adj R-Sq 0.9998 Coeff Var 0.08930
Parameter Estimates
Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 -4.51541 0.06114 -73.85 <.0001 X1 1 3.09701 0.01227 252.31 <.0001 X2 1 1.03186 0.00368 280.08 <.0001
Inputting the New York Rivers data, p. 10.
data p010;
length river $ 20 ;
input river x1 x2 x3 x4 y;
label x1 = 'Agriculture'
x2 = 'Forest'
x3 = 'Residential'
x4 = 'Commercial/Industrial'
y = 'Nitrogen';
cards;
Olean 26 63 1.2 0.29 1.1
Cassadaga 29 57 0.7 0.09 1.01
Oatka 54 26 1.8 0.58 1.9
Neversink 2 84 1.9 1.98 1
Hackensack 3 27 29.4 3.11 1.99
Wappinger 19 61 3.4 0.56 1.42
Fishkill 16 60 5.6 1.11 2.04
Honeoye 40 43 1.3 0.24 1.65
Susquehanna 28 62 1.1 0.15 1.01
Chenango 26 60 0.9 0.23 1.21
Tioughnioga 26 53 0.9 0.18 1.33
West_Canada 15 75 0.7 0.16 0.75
East_Canada 6 84 0.5 0.12 0.73
Saranac 3 81 0.8 0.35 0.8
Ausable 2 89 0.7 0.35 0.76
Black 6 82 0.5 0.15 0.87
Schoharie 22 70 0.9 0.22 0.8
Raquette 4 75 0.4 0.18 0.87
Oswegatchie 21 56 0.5 0.13 0.66
Cohocton 40 49 1.1 0.13 1.25
;
run;
Table 4.2, p. 99
proc reg data = p010; model y = x1-x4; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: y NitrogenAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F Model 4 2.56985 0.64246 9.15 0.0006 Error 15 1.05273 0.07018 Corrected Total 19 3.62257
Root MSE 0.26492 R-Square 0.7094 Dependent Mean 1.15750 Adj R-Sq 0.6319 Coeff Var 22.88715 Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t| Intercept Intercept 1 1.72221 1.23408 1.40 0.1832 x1 Agriculture 1 0.00581 0.01503 0.39 0.7046 x2 Forest 1 -0.01297 0.01393 -0.93 0.3667 x3 Residential 1 -0.00723 0.03383 -0.21 0.8337 x4 Commercial/Industrial 1 0.30503 0.16382 1.86 0.0823
Excluding the observation where River = Neversink.
proc reg data = p010; model y = x1-x4; where river ~= 'Neversink'; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: y NitrogenAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F Model 4 3.07765 0.76941 20.76 <.0001 Error 14 0.51881 0.03706 Corrected Total 18 3.59646
Root MSE 0.19250 R-Square 0.8557 Dependent Mean 1.16579 Adj R-Sq 0.8145 Coeff Var 16.51280 Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t| Intercept Intercept 1 1.09947 0.91164 1.21 0.2478 x1 Agriculture 1 0.01014 0.01098 0.92 0.3717 x2 Forest 1 -0.00759 0.01022 -0.74 0.4701 x3 Residential 1 -0.12379 0.03934 -3.15 0.0071 x4 Commercial/Industrial 1 1.52896 0.34372 4.45 0.0006
Excluding the observation where River = Hackensack.
proc reg data = p010; model y = x1-x4; where river ~= 'Hackensack'; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: y NitrogenAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F Model 4 2.49968 0.62492 22.24 <.0001 Error 14 0.39336 0.02810 Corrected Total 18 2.89304
Root MSE 0.16762 R-Square 0.8640 Dependent Mean 1.11368 Adj R-Sq 0.8252 Coeff Var 15.05109
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t| Intercept Intercept 1 1.62601 0.78109 2.08 0.0562 x1 Agriculture 1 0.00235 0.00954 0.25 0.8088 x2 Forest 1 -0.01276 0.00881 -1.45 0.1698 x3 Residential 1 0.18116 0.04439 4.08 0.0011 x4 Commercial/Industrial 1 0.07562 0.11396 0.66 0.5177
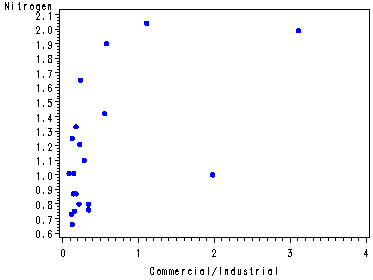
Fig. 4.5, p. 102.
symbol v=dot h=.8 c=blue; proc gplot data = p010; plot y*x4; run; quit;
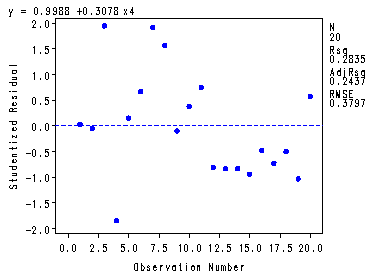
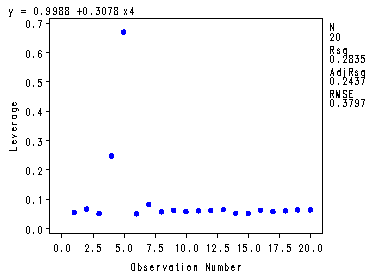
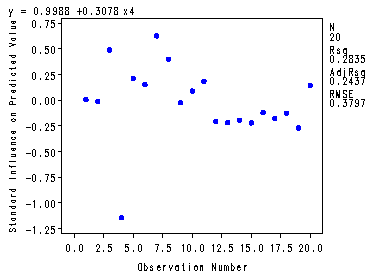
Fig. 4.6, p. 102-103.
proc reg data = p010 noprint; model y=x4; plot student.*obs. h.*obs.; output out=resid student=stdresid H=leverage; run; quit;
Table 4.3, p. 103. The standardized residuals and the leverage values.
proc print data = resid; var stdresid leverage; run;
Obs stdresid leverage1 0.03228 0.05469 2 -0.04502 0.06670 3 1.95292 0.05038 4 -1.84723 0.24787 5 0.15529 0.67101 6 0.67231 0.05018 7 1.92326 0.08261 8 1.56562 0.05700 9 -0.09515 0.06232 10 0.38082 0.05752 11 0.74924 0.06038 12 -0.81033 0.06166 13 -0.83246 0.06443 14 -0.82939 0.05253 15 -0.93761 0.05253 16 -0.47590 0.06232 17 -0.72323 0.05806 18 -0.50049 0.06038 19 -1.03103 0.06371 20 0.57473 0.06371
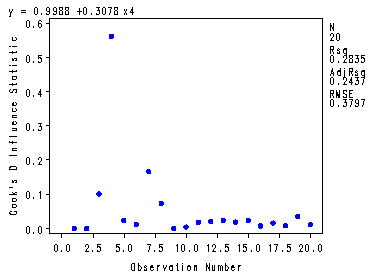
Fig. 4.7(a) and 4.7(b), p. 107.
Plotting the Cook’s Distance and the DFFits.
symbol v=dot h=.8 c=blue; proc reg data = p010 noprint; model y = x4; plot cookd.*obs. dffits.*obs.; output out=resid r=r H=h cookd=CookD dffits=dffits ; run; quit;
Creating the values for the Hadi influence measure.
ods listing close;
proc reg data = p010;
model y = x4;
ods output anova=temp;
run;
quit;
ods listing;
data temp;
set temp;
if source = 'Error' then call symput ('sse', ss);
if source = 'Model' then call symput ('p', df );
run;
%put &sse &p ; /* To make the numbers sse and p appear in the log file. */
data resid2;
set resid;
id = _N_;
newid + 1;
d = .;
d = r/sqrt(&sse);
hadi = h/(1-h) + (&p + 1)*d**2/((1-h)*(1-d**2));
keep hadi d id dffits cookd h;
run;
Table 4.4, p. 106.
proc print data = resid2; var CookD dffits hadi; run;
Obs CookD dffits hadi1 0.00003 0.00755 0.05797 2 0.00007 -0.01170 0.07170 3 0.10118 0.49244 0.58357 4 0.56225 -1.14475 0.77174 5 0.02459 0.21567 2.04228 6 0.01194 0.15210 0.10428 7 0.16653 0.62923 0.59652 8 0.07408 0.40249 0.37293 9 0.00030 -0.02385 0.06747 10 0.00443 0.09180 0.07727 11 0.01804 0.18753 0.12852 12 0.02157 -0.20566 0.14126 13 0.02386 -0.21651 0.14874 14 0.01907 -0.19351 0.13474 15 0.02437 -0.21998 0.15786 16 0.00753 -0.11999 0.09193 17 0.01612 -0.17708 0.12139 18 0.00805 -0.12417 0.09247 19 0.03617 -0.26945 0.19307 20 0.01124 0.14705 0.10539
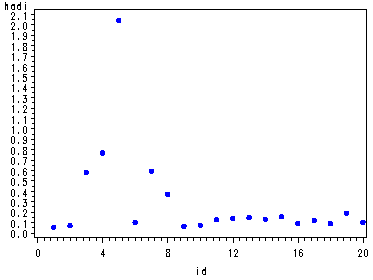
Fig. 4.7(c), p. 107. Plotting the Hadi influence measure.
symbol v=dot h=.8 c=blue; axis2 order=(0 to 20 by 4); proc gplot data = resid2; plot hadi*id / haxis=axis2; run; quit;
>
Creating the potential and residuals.
data resid3; set resid2; po = h/(1-h); re = (1+1)*d**2/( (1-h)*(1-d**2) ); run;
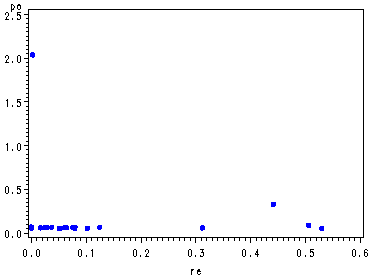
Fig 4.8, p. 108. The Potential-Residual Plot.
symbol v=dot h=.8 c=blue; axis2 order=(0 to 2.5 by .5); proc gplot data = resid3; plot po*re/ vaxis=axis2; run; quit;
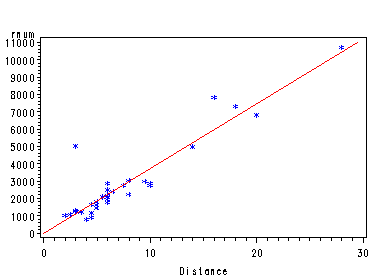
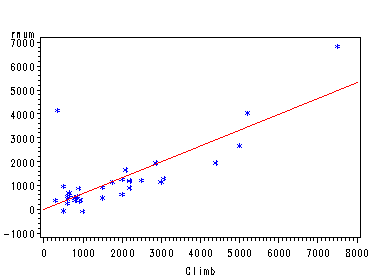
Inputting the Scottish Hills Race data, table 4.5, p. 112
data p112; length Race $ 30; input Race Time Distance Climb; cards; Greenmantle_New_Year_Dash 965 2.5 650 Carnethy 2901 6 2500 Craig_Dunain 2019 6 900 Ben_Rha 2736 7.5 800 Ben_Lomond 3736 8 3070 Goatfell 4393 8 2866 Bens_of_Jura 12277 16 7500 Cairnpapple 2182 6 800 Scolty 1785 5 800 Traprain_Law 2385 6 650 Lairig_Ghru 11560 28 2100 Dollar 2583 5 2000 Lomonds_of_Fife 3900 9.5 2200 Cairn_Table 2648 6 500 Eildon_Two 1616 4.5 1500 Cairngorm 4335 10 3000 Seven_Hills_of_Edinburgh 5905 14 2200 Knock_Hill 4719 3 350 Black_Hill 1045 4.5 1000 Creag_Beag 1954 5.5 600 Kildoon 957 3 300 Meall_Ant_Suiche 1674 3.5 1500 Half_Ben_Nevis 2859 6 2200 Cow_Hill 1076 2 900 North_Berwick_Law 1121 3 600 Creag_Dubh 1573 4 2000 Burnswark 2066 6 800 Largo 1714 5 950 Criffel 3030 6.5 1750 Achmony 1257 5 500 Ben_Nevis 5135 10 4400 Knockfarrel 1943 6 600 Two_Breweries_Fell 10215 18 5200 Cockleroi 1686 4.5 850 Moffat_Chase 9590 20 5000 ; run;
Fig. 4.11(a) and 4.11(b), p. 114. The added-variable plots and generating the output necessary for the residual plus component plots.
proc reg data = p112; model time = distance climb/partial; output out=resid H=h r=r ; ods output anova=temp; run; quit;
The REG Procedure Model: MODEL1 Dependent Variable: TimeAnalysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 2 202712289 101356144 147.51 <.0001 Error 27 18552505 687130 Corrected Total 29 221264794
Root MSE 828.93294 R-Square 0.9162 Dependent Mean 3341.26667 Adj R-Sq 0.9099 Coeff Var 24.80894
Parameter Estimates
Parameter Standard Variable DF Estimate Error t Value Pr > |t|
Intercept 1 -304.14317 263.96279 -1.15 0.2593 Distance 1 395.48217 35.81177 11.04 <.0001 Climb 1 0.40133 0.14962 2.68 0.0123
The REG Procedure Model: MODEL1 Partial Regression Residual Plot
–+—-+—-+—-+—-+—-+—-+—-+—-+—-+—-+—-+—-+—-+—-+—-+—-+—-+– Time | | | | | | | | 4000 + + | | | | | | | 1 | | | | | 3000 + + | | | | | | | | | | | | 2000 + + | | | | | 1 | | | | | | | 1000 + + | | | | | | | | | 1 1 | | 1 1 | 0 + 1 1 1 + | 1 1 1 1 1 | | 11 1 1 | | 1 1 2 1 | | 1 11 1 | | 1 | | 1 | -1000 + 1 + | | | | | | –+—-+—-+—-+—-+—-+—-+—-+—-+—-+—-+—-+—-+—-+—-+—-+—-+—-+– -0.9 -0.8 -0.7 -0.6 -0.5 -0.4 -0.3 -0.2 -0.1 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
Intercept The REG Procedure Model: MODEL1 Partial Regression Residual Plot
—–+—–+—–+—–+—–+—–+—–+—–+—–+—–+—–+—–+—–+—–+—— 8000 + + | 1 | | | | | | | | | | | 6000 + + | | | | | | | | | | | | 4000 + + | | | 1 | Time | | | | | | | | 2000 + + | 1 1 | | 1 | | 1 | | | | 1 | | 11 | 0 + 2 + | 1 2 1 3 | | 1 | | 11 1 | | 21 | | 1 1 | | 1 | -2000 + + | 1 1 | | | | | | | | | | | -4000 + + —–+—–+—–+—–+—–+—–+—–+—–+—–+—–+—–+—–+—–+—–+—— -6 -4 -2 0 2 4 6 8 10 12 14 16 18 20
Distance The REG Procedure Model: MODEL1 Partial Regression Residual Plot
——+——+——+——+——+——+——+——+——+——+——+——+—— 4000 + + | | | | | | | 1 | | | | | 3000 + + | | | | | | | | | | | | 2000 + 1 + | | | | Time | | | | | | | | 1000 + + | 1 | | 1 | | 1 | | 1 | | 1 | | 1 1 1 | 0 + 1 + | 1 1 11 | | 1 1 1 11 | | 1 1 2 | | 11 | | 1 | | 1 | -1000 + 1 + | 1 | | | | | | | | | | | -2000 + + ——+——+——+——+——+——+——+——+——+——+——+——+—— -3000 -2500 -2000 -1500 -1000 -500 0 500 1000 1500 2000 2500
Climb
Fig. 4.12, the partial residual plot for each predictor.
Note: Invoking the par_resid_plot macro which will generate only one plot at a time.
%par_resid_plot(p112, time, climb distance, distance)
%par_resid_plot(p112, time, climb distance, climb)
Generating the variables to be used in the Potential-Residual plot.
data temp;
set temp;
if source = 'Error' then call symput ('sse', ss);
run;
data resid2;
set resid;
d = .;
d = r/sqrt(&sse);
po = h/(1-h);
re = 3*d**2/( (1-h)*(1-d**2) );
run;
It is 3 times d squared since d squared is multiplied by the number of predictors in the model + 1, i.e., p + 1 (which in this case is 2+1 = 3). The Potential-Residual Plot, fig. 4.13, p. 114.
symbol v=dot h=.8 c=blue; proc gplot data = resid2; plot po*re ; run; quit;