Regression Analysis by Example by Chatterjee, Hadi and Price Chapter 9: Analysis of Collinear Data

The Equal Education Opportunity data, table 9.1-9.2, p. 228-229.

data p228;
  input ACHV FAM PEER SCHOOL  ;
cards;
-0.43148  0.60814  0.03509  0.16607 
0.79969  0.79369  0.47924  0.53356 
-0.92467  -0.82630  -0.61951  -0.78635 
-2.19081  -1.25310  -1.21675  -1.04076 
-2.84818  0.17399  -0.18517  0.14229 
-0.66233  0.20246  0.12764  0.27311 
2.63674  0.24184  -0.09022  0.04967 
2.35847  0.59421  0.21750  0.51876 
-0.91305  -0.61561  -0.48971  -0.63219 
0.59445  0.99391  0.62228  0.93368 
1.21073  1.21721  1.00627  1.17381 
1.87164  0.41436  0.71103  0.58978 
-0.10178  0.83782  0.74281  0.72154 
-2.87949  -0.75512  -0.64411  -0.56986 
3.92590  -0.37407  -0.13787  -0.21770 
4.35084  1.40353  1.14085  1.37147 
1.57922  1.64194  1.29229  1.40269 
3.95689  -0.31304  -0.07980  -0.21455 
1.09275  1.28525  1.22441  1.20428 
-0.62389  -1.51938  -1.27565  -1.36598 
-0.63654  -0.38224  -0.05353  -0.35560 
-2.02659  -0.19186  -0.42605  -0.53718 
-1.46692  1.27649  0.81427  0.91967 
3.15078  0.52310  0.30720  0.47231 
-2.18938  -1.59810  -1.01572  -1.48315 
1.91715  0.77914  0.87771  0.76496 
-2.71428  -1.04745  -0.77536  -0.91397 
-6.59852  -1.63217  -1.47709  -1.71347 
0.65101  0.44328  0.60956  0.32833 
-0.13772  -0.24972  0.07876  -0.17216 
-2.43959  -0.33480  -0.39314  -0.37198 
-3.27802  -0.20680  -0.13936  0.05626 
-2.48058  -1.99375  -1.69587  -1.87838 
1.88639  0.66475  0.79670  0.69865 
5.06459  -0.27977  0.10817  -0.26450 
1.96335  -0.43990  -0.66022  -0.58490 
0.26274  -0.05334  -0.02396  -0.16795 
-2.94593  -2.06699  -1.31832  -1.72082 
-1.38628  -1.02560  -1.15858  -1.19420 
-0.20797  0.45847  0.21555  0.31347 
-1.07820  0.93979  0.63454  0.69907 
-1.66386  -0.93238  -0.95216  -1.02725 
0.58117  -0.35988  -0.30693  -0.46232 
1.37447  -0.00518  0.35985  0.02485 
-2.82687  -0.18892  -0.07959  0.01704 
3.86363  0.87271  0.47644  0.57036 
-2.64141  -2.06993  -1.82915  -2.16738 
0.05387  0.32143  -0.25961  0.21632 
0.50763  -1.42382  -0.77620  -1.07473 
0.64347  -0.07852  -0.21347  -0.11750 
2.49414  -0.14925  -0.03192  -0.36598 
0.61955  0.52666  0.79149  0.71369 
0.61745  -1.49102  -1.02073  -1.38103 
-1.00743  -0.94757  -1.28991  -1.24799 
-0.37469  0.24550  0.83794  0.59596 
-2.52824  -0.41630  -0.60312  -0.34951 
0.02372  1.38143  1.54542  1.59429 
2.51077  1.03806  0.91637  0.97602 
-4.22716  -0.88639  -0.47652  -0.77693 
1.96847  1.08655  0.65700  0.89401 
1.25668  -1.95142  -1.94199  -1.89645 
-0.16848  2.83384  2.47398  2.79222 
-0.34158  1.86753  1.55229  1.80057 
-2.23973  -1.11172  -0.69732  -0.80197 
3.62654  1.41958  1.11481  1.24558 
0.97034  0.53940  0.16182  0.33477 
3.16093  0.22491  0.74800  0.66182 
-1.90801  1.48244  1.47079  1.54283 
0.64598  2.05425  1.80369  1.90066 
-1.75915  1.24058  0.64484  0.87372 
;
run;

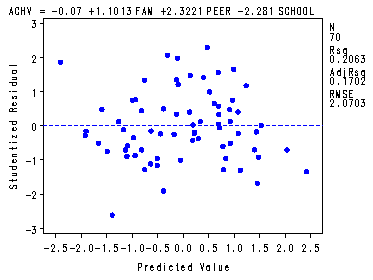
Table 9.3 and fig. 9.1, p. 229.

symbol v=dot h=.8 c=blue;
proc reg data = p228;
  model achv = fam peer school;
  plot student.*p.;
run;
quit;

The REG Procedure Model: MODEL1 Dependent Variable: ACHV

Analysis of Variance

Sum of Mean Source DF Squares Square F Value Pr > F Model 3 73.50623 24.50208 5.72 0.0015 Error 66 282.87323 4.28596 Corrected Total 69 356.37946

Root MSE 2.07026 R-Square 0.2063 Dependent Mean 0.01919 Adj R-Sq 0.1702 Coeff Var 10788 Parameter Estimates

Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 -0.06996 0.25064 -0.28 0.7810 FAM 1 1.10126 1.41056 0.78 0.4378 PEER 1 2.32206 1.48129 1.57 0.1218 SCHOOL 1 -2.28100 2.22045 -1.03 0.3080

The correlations displayed in fig. 9.2, p. 231.

proc corr data=p228;
 var fam peer school;
run;

The CORR Procedure 3 Variables: FAM PEER SCHOOL Simple Statistics

Variable N Mean Std Dev Sum Minimum Maximum FAM 70 0.04938 1.08315 3.45683 -2.06993 2.83384 PEER 70 0.04631 0.92480 3.24199 -1.94199 2.47398 SCHOOL 70 0.03191 1.02354 2.23345 -2.16738 2.79222 Pearson Correlation Coefficients, N = 70 Prob > |r| under H0: Rho=0

FAM PEER SCHOOL FAM 1.00000 0.96008 0.98568 <.0001 <.0001

PEER 0.96008 1.00000 0.98216 <.0001 <.0001

SCHOOL 0.98568 0.98216 1.00000 <.0001 <.0001

Fig. 9.2, p. 231.
Note: Proc insight was not actually invoked here because it has to be terminated manually. If the quit statement is added it will not display the graph.

proc insight data = p228;
  scatter fam peer school * fam peer school;
run;

Import data, table 9.5, p. 233.

data p233;
  input YEAR IMPORT DOPROD STOCK CONSUM;
cards;
49 15.9 149.3 4.2 108.1
50 16.4 161.2 4.1 114.8
51 19 171.5 3.1 123.2
52 19.1 175.5 3.1 126.9
53 18.8 180.8 1.1 132.1
54 20.4 190.7 2.2 137.7
55 22.7 202.1 2.1 146
56 26.5 212.4 5.6 154.1
57 28.1 226.1 5 162.3
58 27.6 231.9 5.1 164.3
59 26.3 239 0.7 167.6
60 31.1 258 5.6 176.8
61 33.3 269.8 3.9 186.6
62 37 288.4 3.1 199.7
63 43.3 304.5 4.6 213.9
64 49 323.4 7 223.8
65 50.3 336.8 1.2 232
66 56.6 353.9 4.5 242.9
;
run;

Creating an index variable.

data p233;
  set p233;
  index = _n_;
run;

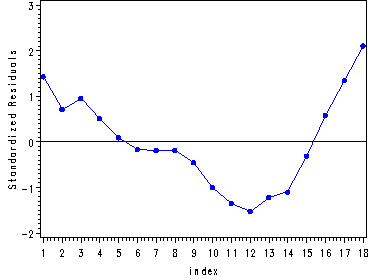
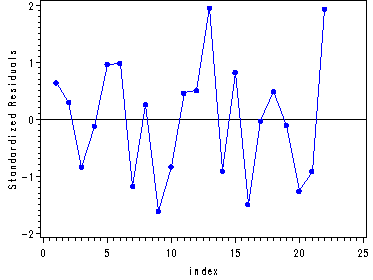
Table 9.6 and fig. 9.3, p. 233.

proc reg data = p233;
  model import = doprod stock consum;
  output out = resid student = stdresid; 
run;
quit;
goptions reset = all;
symbol1 i=join color=blue value=dot h=.8;
axis1 label=(angle =90 'Standardized Residuals');
proc gplot data = resid;
  plot stdresid*index / vaxis=axis1 vref=0;
run;
quit;

The REG Procedure Model: MODEL1 Dependent Variable: IMPORT

Analysis of Variance

Sum of Mean Source DF Squares Square F Value Pr > F

Model 3 2576.92075 858.97358 168.45 <.0001 Error 14 71.39037 5.09931 Corrected Total 17 2648.31111

Root MSE 2.25817 R-Square 0.9730 Dependent Mean 30.07778 Adj R-Sq 0.9673 Coeff Var 7.50775

Parameter Estimates

Parameter Standard Variable DF Estimate Error t Value Pr > |t|

Intercept 1 -19.72511 4.12525 -4.78 0.0003 DOPROD 1 0.03220 0.18688 0.17 0.8656 STOCK 1 0.41420 0.32226 1.29 0.2195 CONSUM 1 0.24275 0.28536 0.85 0.4093

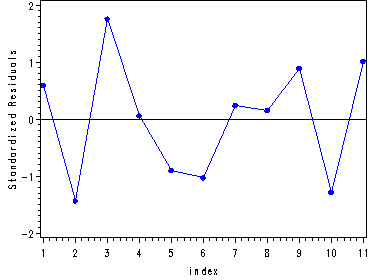
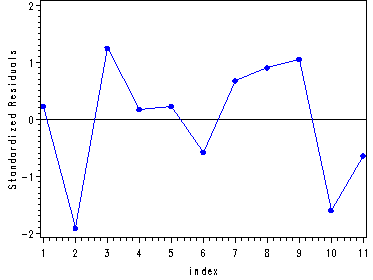
Table 9.7, p. 239 and fig. 9.4, p. 233.

proc reg data = p233;
   where year LE 59;
   model import = doprod stock consum;
   output out=resid student=stdresid;
run;
quit;
goptions reset = all;
symbol1 i=join color=blue value=dot h=.8;
axis1 label=(angle =90 'Standardized Residuals');
proc gplot data = resid;
  plot stdresid*index / vaxis=axis1 vref=0;
run;
quit;

The REG Procedure Model: MODEL1 Dependent Variable: IMPORT

Analysis of Variance

Sum of Mean Source DF Squares Square F Value Pr > F Model 3 204.77614 68.25871 285.61 <.0001 Error 7 1.67295 0.23899 Corrected Total 10 206.44909

Root MSE 0.48887 R-Square 0.9919 Dependent Mean 21.89091 Adj R-Sq 0.9884 Coeff Var 2.23321 Parameter Estimates

Parameter Standard Variable DF Estimate Error t Value Pr > |t|

Intercept 1 -10.12799 1.21216 -8.36 <.0001 DOPROD 1 -0.05140 0.07028 -0.73 0.4883 STOCK 1 0.58695 0.09462 6.20 0.0004 CONSUM 1 0.28685 0.10221 2.81 0.0263

Table 9.8, p. 237.

ods listing close;
proc reg data = p233;
  where year LE 59;
   model import = doprod;
   model import = stock;
   model import = consum;
   model import = doprod stock;
   model import = doprod consum;
   model import = stock consum;
   model import = doprod stock consum;
   ods output  ParameterEstimates=temp;
run;
quit;
ods output close;
ods listing;
data temp;
  set temp;
  keep model variable estimate;
run;
proc transpose data = temp out=wide1;
 by model;
 var variable estimate;
run;
proc print data = wide1;
  var model col1-col4;
run;

Obs Model COL1 COL2 COL3 COL4

1 MODEL1 Intercept DOPROD 2 MODEL1 -6.55810 0.14620 3 MODEL2 Intercept STOCK 4 MODEL2 19.61124 0.69081 5 MODEL3 Intercept CONSUM 6 MODEL3 -8.01325 0.21400 7 MODEL4 Intercept DOPROD STOCK 8 MODEL4 -8.44014 0.14531 0.62248 9 MODEL5 Intercept DOPROD CONSUM 10 MODEL5 -8.88431 -0.10875 0.37168 11 MODEL6 Intercept STOCK CONSUM 12 MODEL6 -9.74274 0.59605 0.21230 13 MODEL7 Intercept DOPROD STOCK CONSUM 14 MODEL7 -10.12799 -0.05140 0.58695 0.28685

Advertising data, table 9.9, p. 238. Creating the index variable.

data p238;
  input S_t A_t P_t E_t A_t_1 P_t_1 ;
cards;
20.11371 1.98786 1.0 0.30 2.01722 0.0 
15.10439 1.94418 0.0 0.30 1.98786 1.0 
18.68375 2.19954 0.8 0.35 1.94418 0.0 
16.05173 2.00107 0.0 0.35 2.19954 0.8 
21.30101 1.69292 1.3 0.30 2.00107 0.0 
17.85004 1.74334 0.3 0.32 1.69292 1.3 
18.87558 2.06907 1.0 0.31 1.74334 0.3 
21.26599 1.01709 1.0 0.41 2.06907 1.0 
20.48473 2.01906 0.9 0.45 1.01709 1.0 
20.54032 1.06139 1.0 0.45 2.01906 0.9 
26.18441 1.45999 1.5 0.50 1.06139 1.0 
21.71606 1.87511 0.0 0.60 1.45999 1.5 
28.69595 2.27109 0.8 0.65 1.87511 0.0 
25.83720 1.11191 1.0 0.65 2.27109 0.8 
29.31987 1.77407 1.2 0.65 1.11191 1.0 
24.19041 0.95878 1.0 0.65 1.77407 1.2 
26.58966 1.98930 1.0 0.62 0.95878 1.0 
22.24466 1.97111 0.0 0.60 1.98930 1.0 
24.79944 2.26603 0.7 0.60 1.97111 0.0 
21.19105 1.98346 0.1 0.61 2.26603 0.7 
26.03441 2.10054 1.0 0.60 1.98346 0.1 
27.39304 1.06815 1.0 0.58 2.10054 1.0 
;
run;

Creating the index variable.

data p238 ;
  set p238;
  index = _n_;
run;

Coefficients for equation on bottom of p. 238.

proc reg data = p238;
  model A_t = P_t P_t_1 A_t_1;
run;
quit;

The REG Procedure Model: MODEL1 Dependent Variable: A_t

Analysis of Variance

Sum of Mean Source DF Squares Square F Value Pr > F Model 3 3.85945 1.28648 213.62 <.0001 Error 18 0.10840 0.00602 Corrected Total 21 3.96786

Root MSE 0.07760 R-Square 0.9727 Dependent Mean 1.75296 Adj R-Sq 0.9681 Coeff Var 4.42706 Parameter Estimates

Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 4.63124 0.12937 35.80 <.0001 P_t 1 -0.86953 0.04333 -20.07 <.0001 P_t_1 1 -0.94689 0.04192 -22.59 <.0001 A_t_1 1 -0.86340 0.05024 -17.19 <.0001

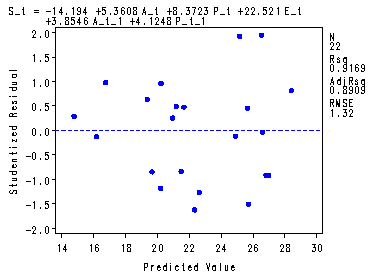
Table 9.10 and fig. 9.5-9.6, p. 239-240.

goptions reset = all;
symbol1 color=blue value=dot h=.8;
proc reg data = p238  ;
  model S_t = A_t P_t E_t A_t_1 P_t_1 ;
  plot student.*p.;
  output out=resid student=stdresid;
run;
quit;

The REG Procedure Model: MODEL1 Dependent Variable: S_t

Analysis of Variance

Sum of Mean Source DF Squares Square F Value Pr > F Model 5 307.57179 61.51436 35.30 <.0001 Error 16 27.87870 1.74242 Corrected Total 21 335.45049

Root MSE 1.32001 R-Square 0.9169 Dependent Mean 22.47579 Adj R-Sq 0.8909 Coeff Var 5.87302 Parameter Estimates

Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 -14.19366 18.71511 -0.76 0.4592 A_t 1 5.36075 4.02769 1.33 0.2019 P_t 1 8.37232 3.58641 2.33 0.0329 E_t 1 22.52103 2.14235 10.51 <.0001 A_t_1 1 3.85457 3.57772 1.08 0.2973 P_t_1 1 4.12479 3.89511 1.06 0.3053

goptions reset = all;
symbol1 i=join color=blue value=dot h=.8;
axis1 label=(angle =90 'Standardized Residuals');
axis2  order=(0 to 25 by 5);
proc gplot data = resid;
  plot stdresid*index / haxis=axis2 vaxis=axis1 vref=0;
run;
quit;

Table 9.11, p. 239.

proc corr data = p238;
var A_t P_t E_t A_t_1 P_t_1;
run;

The CORR Procedure 5 Variables: A_t P_t E_t A_t_1 P_t_1 Simple Statistics

Variable N Mean Std Dev Sum Minimum Maximum A_t 22 1.75296 0.43468 38.56506 0.95878 2.27109 P_t 22 0.75455 0.46468 16.60000 0 1.50000 E_t 22 0.49318 0.13947 10.85000 0.30000 0.65000 A_t_1 22 1.79610 0.40987 39.51413 0.95878 2.27109 P_t_1 22 0.70909 0.48786 15.60000 0 1.50000

Pearson Correlation Coefficients, N = 22 Prob > |r| under H0: Rho=0

A_t P_t E_t A_t_1 P_t_1 A_t 1.00000 -0.35695 -0.12852 -0.13974 -0.49599 0.1029 0.5687 0.5351 0.0189

P_t -0.35695 1.00000 0.06259 -0.31647 -0.29636 0.1029 0.7820 0.1513 0.1805

E_t -0.12852 0.06259 1.00000 -0.16643 0.20811 0.5687 0.7820 0.4592 0.3527

A_t_1 -0.13974 -0.31647 -0.16643 1.00000 -0.35776 0.5351 0.1513 0.4592 0.1021

P_t_1 -0.49599 -0.29636 0.20811 -0.35776 1.00000 0.0189 0.1805 0.3527 0.1021

Table 9.12, p. 242.

ods listing close;
proc reg data = p228 ;
  model achv = fam peer school / vif;
  ods output  ParameterEstimates=temp1;
run;
ods output close;
ods listing;
data temp1;
  set temp1;
  keep dataname variable varianceinflation ;
  dataname = 'EEO';
run;
ods listing close;
proc reg data = p233 ;
  model import = doprod stock consum / vif;
  ods output  ParameterEstimates=temp2;
run;
ods listing;
data temp2;
  set temp2;
  keep dataname variable varianceinflation ;
  dataname = 'Import';
run;
ods listing close;
proc reg data = p238;
   model S_t = A_t P_t E_t A_t_1 P_t_1  / vif;
  ods output  ParameterEstimates=temp3;
run;
ods listing;
data temp3;
  set temp3;
  keep dataname variable varianceinflation ;
  dataname = 'Advertising';
run;
data mtemp;
  set temp1 temp2 temp3;
run;
proc print data= mtemp;
  var dataname variable varianceinflation;
run;

Variance Obs dataname Variable Inflation

1 EEO Intercept 0 2 EEO FAM 37.58064 3 EEO PEER 30.21166 4 EEO SCHOOL 83.15544 5 Imp Intercept 0 6 Imp DOPROD 469.74214 7 Imp STOCK 1.04988 8 Imp CONSUM 469.37134 9 Adv Intercept 0 10 Adv A_t 36.94151 11 Adv P_t 33.47351 12 Adv E_t 1.07596 13 Adv A_t_1 25.91565 14 Adv P_t_1 43.52097

Covariance matrix and correlation matrix on p. 244.

proc corr data = p233 cov;
where year <= 59;
var doprod  stock consum;
run;

The CORR Procedure 3 Variables: DOPROD STOCK CONSUM Covariance Matrix, DF = 10

DOPROD STOCK CONSUM DOPROD 899.9709091 1.2790000 617.3263636 STOCK 1.2790000 2.7200000 1.2140000 CONSUM 617.3263636 1.2140000 425.7785455 Simple Statistics

Variable N Mean Std Dev Sum Minimum Maximum DOPROD 11 194.59091 29.99952 2141 149.30000 239.00000 STOCK 11 3.30000 1.64924 36.30000 0.70000 5.60000 CONSUM 11 139.73636 20.63440 1537 108.10000 167.60000 Pearson Correlation Coefficients, N = 11 Prob > |r| under H0: Rho=0

DOPROD STOCK CONSUM DOPROD 1.00000 0.02585 0.99726 0.9399 <.0001

STOCK 0.02585 1.00000 0.03567 0.9399 0.9171

CONSUM 0.99726 0.03567 1.00000 <.0001 0.9171

The Eigenvalues and Eigenvectors on bottom of p. 246 and principal components in table 9.13, p. 247.
Note: Some of the eigenvectors are the additive inverse of those in the book which is due to the fact that eigenvectors are unique up to a multiple of -1.

ods listing close;
proc princomp  data = p233 out=temp ;
 where year <= 59;
 var doprod stock consum;
 ods output  Eigenvectors=temp1;
run;
ods listing;
proc print data = temp1;
run;
proc print data = temp;
  var prin1-prin3;
run;

Obs Variable Prin1 Prin2 Prin3

1 DOPROD 0.706330 -.035689 0.706982 2 STOCK 0.043501 0.999029 0.006971 3 CONSUM 0.706544 -.025830 -.707197 Obs Prin1 Prin2 Prin3

1 -2.12589 0.63866 0.020722 2 -1.61893 0.55554 0.071113 3 -1.11517 -0.07298 0.021730 4 -0.89430 -0.08237 -0.010813 5 -0.64421 -1.30669 -0.072582 6 -0.19035 -0.65915 -0.026553 7 0.35962 -0.74367 -0.042781 8 0.97180 1.35406 -0.062863 9 1.55932 0.96405 -0.023574 10 1.76700 1.01522 0.044988 11 1.93110 -1.66266 0.080613

Creating newvar, p. 250.

data p233;
  set p233;
  newvar = doprod + consum;
run;

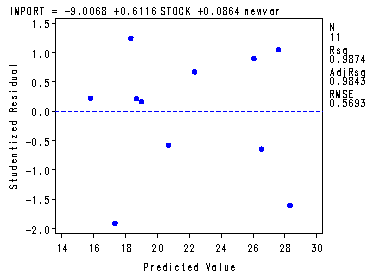
Table 9.14 and fig. 9.7-9.8, p. 250-251.

symbol1 c=blue v=dot h=.8;
proc reg data = p233;
  where year <= 59;
  model import = stock newvar;
  plot student.*p.;
  output out=resid student=stdresid;
run;
quit;
 
symbol1 c=blue v=dot h=.8;
symbol1 i=join color=blue value=dot h=.8;
axis1 label=(angle =90 'Standardized Residuals');
axis2  order=(0 to 25 by 5);
proc gplot data = resid;
  plot stdresid*index / vaxis=axis1 vref=0;
run;
quit;

The REG Procedure Model: MODEL1 Dependent Variable: IMPORT

Analysis of Variance

Sum of Mean Source DF Squares Square F Value Pr > F Model 2 203.85592 101.92796 314.45 <.0001 Error 8 2.59317 0.32415 Corrected Total 10 206.44909

Root MSE 0.56934 R-Square 0.9874 Dependent Mean 21.89091 Adj R-Sq 0.9843 Coeff Var 2.60080 Parameter Estimates

Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 -9.00680 1.24502 -7.23 <.0001 STOCK 1 0.61164 0.10921 5.60 0.0005 newvar 1 0.08638 0.00356 24.27 <.0001

Beware of all the typos on p. 250, please refer to the Errata web page. The correlation, eigenvalues and eigenvectors of stock and newvar, p. 250.

proc princomp data = p233;
  where year <= 59;
  var stock newvar;
run;

The PRINCOMP Procedure Observations 11 Variables 2 Simple Statistics

STOCK newvar Mean 3.300000000 334.3272727 StD 1.649242250 50.6004168 Correlation Matrix

STOCK newvar STOCK 1.0000 0.0299 newvar 0.0299 1.0000

Eigenvalues of the Correlation Matrix

Eigenvalue Difference Proportion Cumulative 1 1.02987334 0.05974667 0.5149 0.5149 2 0.97012666 0.4851 1.0000 Eigenvectors

Prin1 Prin2 STOCK 0.707107 0.707107 newvar 0.707107 -.707107

Table 9.15, p. 253.

proc reg data = p233;
  where year <= 59;
  model import = doprod stock ;
run;
quit;

The REG Procedure Model: MODEL1 Dependent Variable: IMPORT

Analysis of Variance

Sum of Mean Source DF Squares Square F Value Pr > F Model 2 202.89371 101.44685 228.27 <.0001 Error 8 3.55538 0.44442 Corrected Total 10 206.44909

Root MSE 0.66665 R-Square 0.9828 Dependent Mean 21.89091 Adj R-Sq 0.9785 Coeff Var 3.04533 Parameter Estimates

Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 -8.44014 1.43518 -5.88 0.0004 DOPROD 1 0.14531 0.00703 20.67 <.0001 STOCK 1 0.62248 0.12787 4.87 0.0012

The PC coefficients for equations in 9.27, p. 253.
Note: The eigenvectors are unique up to a multiple of -1.

proc princomp data = p238 out = temp;
  var A_t P_t E_t A_t_1 P_t_1;
run;

The PRINCOMP Procedure Observations 22 Variables 5 Simple Statistics

A_t P_t E_t A_t_1 P_t_1 Mean 1.752957273 0.7545454545 0.4931818182 1.796096818 0.7090909091 StD 0.434678765 0.4646834793 0.1394679128 0.409865806 0.4878613102

Correlation Matrix

A_t P_t E_t A_t_1 P_t_1 A_t 1.0000 -.3570 -.1285 -.1397 -.4960 P_t -.3570 1.0000 0.0626 -.3165 -.2964 E_t -.1285 0.0626 1.0000 -.1664 0.2081 A_t_1 -.1397 -.3165 -.1664 1.0000 -.3578 P_t_1 -.4960 -.2964 0.2081 -.3578 1.0000

Eigenvalues of the Correlation Matrix

Eigenvalue Difference Proportion Cumulative 1 1.70095474 0.41274783 0.3402 0.3402 2 1.28820691 0.14355527 0.2576 0.5978 3 1.14465164 0.28573629 0.2289 0.8268 4 0.85891534 0.85164396 0.1718 0.9985 5 0.00727138 0.0015 1.0000 Eigenvectors

Prin1 Prin2 Prin3 Prin4 Prin5 A_t -.532445 -.023790 0.667740 0.074417 0.514316 P_t 0.232452 0.824945 -.157793 -.037107 0.489036 E_t 0.389086 -.022080 0.217210 0.894902 -.009710 A_t_1 -.395228 -.259638 -.691911 0.338018 0.428236 P_t_1 0.595714 -.501000 0.057474 -.279247 0.559323

The PC’s found by SAS were the additive inverses of those in the book. For a quick fix to get them to be exactly the same just transform them by -1.

proc print data = temp (obs = 10);
  var prin1-prin5;
run;
data temp1;
  set temp;
  prin1 = -1*prin1;
  prin3 = -1*prin3;
  prin5 = -1*prin5;
run;
proc print data = temp1 (obs = 10);
  var prin1-prin5;
run;

Obs Prin1 Prin2 Prin3 Prin4 Prin5

1 -1.78296 1.04159 -0.48019 -0.63071 -0.03222 2 -0.98031 -1.73963 -0.04034 -1.15494 -0.02050 3 -1.93238 0.71330 0.11408 -0.31791 -0.07203 4 -1.35884 -1.67937 -0.25599 -0.53532 0.03520 5 -1.25604 1.60055 -1.00787 -0.71848 -0.08235 6 0.12229 -1.32047 0.11365 -1.49990 0.09198 7 -1.22412 0.90098 0.15783 -0.95023 0.12096 8 0.88410 0.01753 -1.76986 -0.62071 0.01215 9 0.73275 0.44523 1.64148 -1.05210 -0.00946 10 0.86754 0.14315 -1.56687 -0.34047 -0.10512

Obs Prin1 Prin2 Prin3 Prin4 Prin5

1 1.78296 1.04159 0.48019 -0.63071 0.03222 2 0.98031 -1.73963 0.04034 -1.15494 0.02050 3 1.93238 0.71330 -0.11408 -0.31791 0.07203 4 1.35884 -1.67937 0.25599 -0.53532 -0.03520 5 1.25604 1.60055 1.00787 -0.71848 0.08235 6 -0.12229 -1.32047 -0.11365 -1.49990 -0.09198 7 1.22412 0.90098 -0.15783 -0.95023 -0.12096 8 -0.88410 0.01753 1.76986 -0.62071 -0.01215 9 -0.73275 0.44523 -1.64148 -1.05210 0.00946 10 -0.86754 0.14315 1.56687 -0.34047 0.10512

Table 9.16, p. 256. The estimated coefficients in the table 9.16 correspond to the standardized estimates in the output.

proc reg data = p238;
  model S_t = A_t P_t E_t A_t_1 P_t_1/stb;
run;
quit;

The REG Procedure Model: MODEL1 Dependent Variable: S_t

Analysis of Variance

Sum of Mean Source DF Squares Square F Value Pr > F Model 5 307.57179 61.51436 35.30 <.0001 Error 16 27.87870 1.74242 Corrected Total 21 335.45049

Root MSE 1.32001 R-Square 0.9169 Dependent Mean 22.47579 Adj R-Sq 0.8909 Coeff Var 5.87302 Parameter Estimates

Parameter Standard Standardized Variable DF Estimate Error t Value Pr > |t| Estimate Intercept 1 -14.19366 18.71511 -0.76 0.4592 0 A_t 1 5.36075 4.02769 1.33 0.2019 0.58303 P_t 1 8.37232 3.58641 2.33 0.0329 0.97342 E_t 1 22.52103 2.14235 10.51 <.0001 0.78588 A_t_1 1 3.85457 3.57772 1.08 0.2973 0.39529 P_t_1 1 4.12479 3.89511 1.06 0.3053 0.50349

We thank Yusuf Ma for the following SAS code to replicate the values shown in Table 9.16.

proc reg data=p238;
model s_t = a_t p_t e_t A_t_1 p_t_1/stb;
ods output parameterestimates=temp1;
run;
quit;

data temp1;
set temp1;
label stderr_stb ='s.e.'
variable = 'variable';
if variable = 'Intercept' then delete;
stderr_stb = StandardizedEst/tvalue;
keep variable standardizedest stderr_stb tvalue probt; run;

*to put the variables in the order as the book;

data temp1;
retain variable standardizedest stderr_stb tvalue probt; 
set temp1;
run;


proc print data=temp1 label;
Title 'Regression results obtained from fitting the model in (9.29)'; 
run;
title "";

Regression results obtained from fitting the model in (9.29)                                     3

                                      stderr_
Obs    variable    standardizedest      stb       tvalue     probt

 1      A_t              0.58303      0.43805       1.33    0.2019
 2      P_t              0.97342      0.41698       2.33    0.0329
 3      E_t              0.78588      0.07476      10.51    <.0001
 4      A_t_1            0.39529      0.36690       1.08    0.2973
 5      P_t_1            0.50349      0.47546       1.06    0.3053

Creating the standardized variable for S_t to be used in regression p. 257.

proc sql;  
 create table tempstd as
 select *, (S_t - mean(S_t))/std(S_t) as zs_t
 from temp1;
quit;

Table 9.17, p. 257.
Note: The regression model has no intercept (the noint option in the model statement) because all the variables have been standardized.

proc reg data = tempstd;
  model zs_t = prin1-prin5/noint;
run;
quit;

The REG Procedure Model: MODEL1 Dependent Variable: zs_t NOTE: No intercept in model. R-Square is redefined Analysis of Variance

Sum of Mean Source DF Squares Square F Value Pr > F Model 5 19.25473 3.85095 37.51 <.0001 Error 17 1.74527 0.10266 Uncorrected Total 22 21.00000

Root MSE 0.32041 R-Square 0.9169 Dependent Mean -3.1288E-16 Adj R-Sq 0.8924 Coeff Var -1.02407E17 Parameter Estimates

Parameter Standard Variable DF Estimate Error t Value Pr > |t| Prin1 1 -0.36533 0.05361 -6.81 <.0001 Prin2 1 0.41691 0.06160 6.77 <.0001 Prin3 1 -0.16185 0.06535 -2.48 0.0241 Prin4 1 0.70357 0.07544 9.33 <.0001 Prin5 1 -1.21916 0.81995 -1.49 0.1554