Inputting the Crab data, p. 82-83.
data crab; input color spine width satell weight; if satell>0 then y=1; if satell=0 then y=0; n=1; weight = weight/1000; color = color - 1; if color=4 then dark=0; if color < 4 then dark=1; cards; 3 3 28.3 8 3050 4 3 22.5 0 1550 2 1 26.0 9 2300 4 3 24.8 0 2100 4 3 26.0 4 2600 3 3 23.8 0 2100 2 1 26.5 0 2350 4 2 24.7 0 1900 3 1 23.7 0 1950 4 3 25.6 0 2150 4 3 24.3 0 2150 3 3 25.8 0 2650 3 3 28.2 11 3050 5 2 21.0 0 1850 3 1 26.0 14 2300 2 1 27.1 8 2950 3 3 25.2 1 2000 3 3 29.0 1 3000 5 3 24.7 0 2200 3 3 27.4 5 2700 3 2 23.2 4 1950 2 2 25.0 3 2300 3 1 22.5 1 1600 4 3 26.7 2 2600 5 3 25.8 3 2000 5 3 26.2 0 1300 3 3 28.7 3 3150 3 1 26.8 5 2700 5 3 27.5 0 2600 3 3 24.9 0 2100 2 1 29.3 4 3200 2 3 25.8 0 2600 3 2 25.7 0 2000 3 1 25.7 8 2000 3 1 26.7 5 2700 5 3 23.7 0 1850 3 3 26.8 0 2650 3 3 27.5 6 3150 5 3 23.4 0 1900 3 3 27.9 6 2800 4 3 27.5 3 3100 2 1 26.1 5 2800 2 1 27.7 6 2500 3 1 30.0 5 3300 4 1 28.5 9 3250 4 3 28.9 4 2800 3 3 28.2 6 2600 3 3 25.0 4 2100 3 3 28.5 3 3000 3 1 30.3 3 3600 5 3 24.7 5 2100 3 3 27.7 5 2900 2 1 27.4 6 2700 3 3 22.9 4 1600 3 1 25.7 5 2000 3 3 28.3 15 3000 3 3 27.2 3 2700 4 3 26.2 3 2300 3 1 27.8 0 2750 5 3 25.5 0 2250 4 3 27.1 0 2550 4 3 24.5 5 2050 4 1 27.0 3 2450 3 3 26.0 5 2150 3 3 28.0 1 2800 3 3 30.0 8 3050 3 3 29.0 10 3200 3 3 26.2 0 2400 3 1 26.5 0 1300 3 3 26.2 3 2400 4 3 25.6 7 2800 4 3 23.0 1 1650 4 3 23.0 0 1800 3 3 25.4 6 2250 4 3 24.2 0 1900 3 2 22.9 0 1600 4 2 26.0 3 2200 3 3 25.4 4 2250 4 3 25.7 0 1200 3 3 25.1 5 2100 4 2 24.5 0 2250 5 3 27.5 0 2900 4 3 23.1 0 1650 4 1 25.9 4 2550 3 3 25.8 0 2300 5 3 27.0 3 2250 3 3 28.5 0 3050 5 1 25.5 0 2750 5 3 23.5 0 1900 3 2 24.0 0 1700 3 1 29.7 5 3850 3 1 26.8 0 2550 5 3 26.7 0 2450 3 1 28.7 0 3200 4 3 23.1 0 1550 3 1 29.0 1 2800 4 3 25.5 0 2250 4 3 26.5 1 1967 4 3 24.5 1 2200 4 3 28.5 1 3000 3 3 28.2 1 2867 3 3 24.5 1 1600 3 3 27.5 1 2550 3 2 24.7 4 2550 3 1 25.2 1 2000 4 3 27.3 1 2900 3 3 26.3 1 2400 3 3 29.0 1 3100 3 3 25.3 2 1900 3 3 26.5 4 2300 3 3 27.8 3 3250 3 3 27.0 6 2500 4 3 25.7 0 2100 3 3 25.0 2 2100 3 3 31.9 2 3325 5 3 23.7 0 1800 5 3 29.3 12 3225 4 3 22.0 0 1400 3 3 25.0 5 2400 4 3 27.0 6 2500 4 3 23.8 6 1800 2 1 30.2 2 3275 4 3 26.2 0 2225 3 3 24.2 2 1650 3 3 27.4 3 2900 3 2 25.4 0 2300 4 3 28.4 3 3200 5 3 22.5 4 1475 3 3 26.2 2 2025 3 1 24.9 6 2300 2 2 24.5 6 1950 3 3 25.1 0 1800 3 1 28.0 4 2900 5 3 25.8 10 2250 3 3 27.9 7 3050 3 3 24.9 0 2200 3 1 28.4 5 3100 4 3 27.2 5 2400 3 2 25.0 6 2250 3 3 27.5 6 2625 3 1 33.5 7 5200 3 3 30.5 3 3325 4 3 29.0 3 2925 3 1 24.3 0 2000 3 3 25.8 0 2400 5 3 25.0 8 2100 3 1 31.7 4 3725 3 3 29.5 4 3025 4 3 24.0 10 1900 3 3 30.0 9 3000 3 3 27.6 4 2850 3 3 26.2 0 2300 3 1 23.1 0 2000 3 1 22.9 0 1600 5 3 24.5 0 1900 3 3 24.7 4 1950 3 3 28.3 0 3200 3 3 23.9 2 1850 4 3 23.8 0 1800 4 2 29.8 4 3500 3 3 26.5 4 2350 3 3 26.0 3 2275 3 3 28.2 8 3050 5 3 25.7 0 2150 3 3 26.5 7 2750 3 3 25.8 0 2200 4 3 24.1 0 1800 4 3 26.2 2 2175 4 3 26.1 3 2750 4 3 29.0 4 3275 2 1 28.0 0 2625 5 3 27.0 0 2625 3 2 24.5 0 2000 ; run;
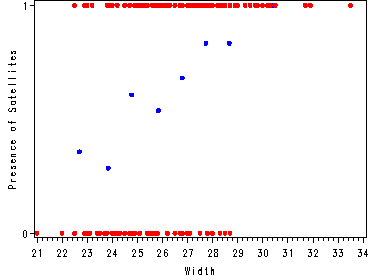
Creating the categorical variable for width and plotting the proportion of satellites and whether satellites are present or not (Y = 1, yes; Y=2, no) versus width.
data crab1;
set crab;
wcat=0;
if width<=23.25 then wcat=1;
if 23.25< width<=24.25 then wcat=2;
if 24.25< width<=25.25 then wcat=3;
if 25.25< width<=26.25 then wcat=4;
if 26.25< width<=27.25 then wcat=5;
if 27.25< width<=28.25 then wcat=6;
if 28.25< width<=29.25 then wcat=7;
if 29.25< width then wcat=8;
run;
proc sql;
create table crab2 as
select *, sum(y)/sum(n) as prop, mean(width) as wmidpt, sum(y) as yes, sum(n) as cases
from crab1
group by wcat;
quit;
proc sort data=crab2;
by width;
run;
goption reset=all;
symbol1 v=dot c=blue h=.7;
symbol2 v=dot c=red h=.7;
axis1 order=(0 1) label=(angle = 90 'Presence of Satellites');
axis2 label=('Width');
proc gplot data=crab2;
plot prop*wmidpt y*width/ overlay vaxis=axis1 haxis=axis2;
run;
quit;
Table 5.1, p. 106.
Note: The variables LCL and UCL are the lower and upper values respectively, of the 95% confidence interval for the predicted probability.
proc logistic data=crab2 desc;
model y = width ;
output out=predict p=pi_hat;
run;
proc sql;
create table pred2 as
select *, sum(pi_hat) as predicted_satell, sum(pi_hat)/sum(n) as predicted_prob
from predict
group by wcat;
quit;
proc sort data=pred2;
by wcat;
run;
data pred3;
set pred2;
by wcat;
if first.wcat;
run;
proc format;
value wcat 1='<=23.25' 2='23.25-24.25' 3='24.25-25.25' 4='25.25-26.25'
5='26.25-27.25' 6='27.25-28.25' 7='28.25-29.25' 8='>29.25';
run;
proc print data = pred3;
format wcat wcat.;
var wcat cases yes prop predicted_prob predicted_satell;
run;
The LOGISTIC ProcedureModel Information Data Set WORK.CRAB2 Response Variable y Number of Response Levels 2 Number of Observations 173 Link Function Logit Optimization Technique Fisher’s scoring Response Profile
Ordered Total Value y Frequency 1 1 111 2 0 62
Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics
Intercept Intercept and Criterion Only Covariates SC 230.912 204.759 -2 Log L 225.759 194.453 Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq Likelihood Ratio 31.3059 1 <.0001 Score 27.8752 1 <.0001 Wald 23.8872 1 <.0001 Analysis of Maximum Likelihood Estimates
Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -12.3508 2.6287 22.0749 <.0001 width 1 0.4972 0.1017 23.8872 <.0001
The LOGISTIC Procedure
Odds Ratio Estimates
Point 95% Wald Effect Estimate Confidence Limits width 1.644 1.347 2.007 Association of Predicted Probabilities and Observed Responses Percent Concordant 73.5 Somers’ D 0.485 Percent Discordant 25.0 Gamma 0.492 Percent Tied 1.5 Tau-a 0.224 Pairs 6882 c 0.742 predicted_ predicted_ Obs wcat cases yes prop prob satell
1 <=23.25 14 5 0.35714 0.25967 3.6354 2 23.25-24.25 14 4 0.28571 0.37900 5.3060 3 24.25-25.25 28 17 0.60714 0.49206 13.7776 4 25.25-26.25 39 21 0.53846 0.62122 24.2277 5 26.25-27.25 22 15 0.68182 0.72445 15.9378 6 27.25-28.25 24 20 0.83333 0.80764 19.3833 7 28.25-29.25 18 15 0.83333 0.86945 15.6502 8 >29.25 14 14 1.00000 0.93443 13.0820
The model can also be estimated using proc genmod as can be seen in the following output. Proc genmod will provide the likelihood ratio confidence interval for all the parameters in the model including chi-squared tests for all the parameters in the model whereas proc logistic will provide the chi-squared tests as well as many other details such as model fit statistics and odds ratios. Another big difference between the two procedures is that proc genmod is a very general procedure that can handle many different distributions and link functions but it does not in general provide a great deal of residuals or built in options that more specific procedures such as proc logistic provides.
proc genmod data=crab; model y = width / dist=bin link=logit waldci lrci; run;
The GENMOD ProcedureModel Information Data Set WORK.CRAB Distribution Binomial Link Function Logit Dependent Variable y Observations Used 173 Probability Modeled Pr( y = 0 ) Response Profile
Ordered Ordered Level Value Count 1 0 62 2 1 111 Criteria For Assessing Goodness Of Fit
Criterion DF Value Value/DF Deviance 171 194.4527 1.1372 Scaled Deviance 171 194.4527 1.1372 Pearson Chi-Square 171 165.1434 0.9658 Scaled Pearson X2 171 165.1434 0.9658 Log Likelihood -97.2263
Algorithm converged. Analysis Of Parameter Estimates
Standard Likelihood Ratio 95% Chi- Parameter DF Estimate Error Confidence Limits Square Pr > ChiSq Intercept 1 12.3508 2.6287 7.4573 17.8097 22.07 <.0001 width 1 -0.4972 0.1017 -0.7090 -0.3084 23.89 <.0001 Scale 0 1.0000 0.0000 1.0000 1.0000 NOTE: The scale parameter was held fixed.
The predicted probabilities discussed at the top of p. 107.
proc logistic data=crab desc noprint; model y = width ; output out=predict p=pi_hat; run; proc print data=predict; where width=21 or width=26.3 or width=33.5; var width pi_hat; run;
Obs width pi_hat14 21.0 0.12910 107 26.3 0.67400 141 33.5 0.98670
Variance and covariance can be obtained by using the covout option in the proc statement and the confidence interval for individual predicted values can be obtained by using the upper and lower options in the model statement. Results p. 110.
proc logistic data=crab2 desc covout outest=temp; model y = width ; output out=predict p=pi_hat upper=ucl lower=lcl; run; proc print data=temp; where _type_='COV'; var _name_ intercept width; run; proc sql; select distinct width, pi_hat, lcl, ucl from predict where width= 26.5 ; quit;
The LOGISTIC ProcedureModel Information Data Set WORK.CRAB2 Response Variable y Number of Response Levels 2 Number of Observations 173 Link Function Logit Optimization Technique Fisher’s scoring Response Profile
Ordered Total Value y Frequency 1 1 111 2 0 62 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics
Intercept Intercept and Criterion Only Covariates AIC 227.759 198.453 SC 230.912 204.759 -2 Log L 225.759 194.453 Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq Likelihood Ratio 31.3059 1 <.0001 Score 27.8752 1 <.0001 Wald 23.8872 1 <.0001 Analysis of Maximum Likelihood Estimates
Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -12.3508 2.6287 22.0749 <.0001 width 1 0.4972 0.1017 23.8872 <.0001
The LOGISTIC Procedure
Odds Ratio Estimates
Point 95% Wald Effect Estimate Confidence Limits width 1.644 1.347 2.007 Association of Predicted Probabilities and Observed Responses Percent Concordant 73.5 Somers’ D 0.485 Percent Discordant 25.0 Gamma 0.492 Percent Tied 1.5 Tau-a 0.224 Pairs 6882 c 0.742 Obs _NAME_ Intercept width
2 Intercept 6.91023 -0.26685 3 width -0.26685 0.01035 Lower 95% Upper 95% Estimated Confidence Confidence width Probability Limit Limit ——————————————— 26.5 0.695465 0.612054 0.767747
Table 5.2, p. 112.
proc sql;
create table pred2 as
select pi_hat, wcat, sum(y) as Num_yes, sum(1-y) as Num_no, sum(pi_hat) as Fitted_yes,
sum(1-pi_hat) as Fitted_no
from predict
group by wcat;
quit;
proc sort data=pred2;
by wcat;
run;
data pred3;
set pred2;
by wcat;
if first.wcat;
run;
proc print data = pred3;
format wcat wcat.;
var wcat Num_yes Num_no Fitted_yes Fitted_no;
run;
Fitted_ Fitted_ Obs wcat Num_yes Num_no yes no1 <=23.25 5 9 3.6354 10.3646 2 23.25-24.25 4 10 5.3060 8.6940 3 24.25-25.25 17 11 13.7776 14.2224 4 25.25-26.25 21 18 24.2277 14.7723 5 26.25-27.25 15 7 15.9378 6.0622 6 27.25-28.25 20 4 19.3833 4.6167 7 28.25-29.25 15 3 15.6502 2.3498 8 >29.25 14 0 13.0820 0.9180
Inputting the grouped Crab data, p. 271.
data grouped; input width cases satell; cards; 22.69 14 5 23.84 14 4 24.77 28 17 25.84 39 21 26.79 22 15 27.74 24 20 28.67 18 15 30.41 14 14 run;
Formatting the variable width to make the output look nice.
proc format;
value width 22.69='<=23.25' 23.84='23.25-24.25' 24.77='24.25-25.25' 25.84='25.25-26.25'
26.79='26.25-27.25' 27.74='27.25-28.25' 28.67='28.25-29.25' 30.41='>29.25';
run;
Likelihood-ratio model comparisons test from the deviance of the model with width as the predictor and the deviance of the model without any predictors, p. 114.
Note: In proc logistic SAS includes the -2log likelihood for the full model and for the model without any predictors. Moreover, the output includes various goodness of fit test in the table labeled Testing Global Null Hypothesis: BETA=0.
proc logistic data=grouped desc; model satell/cases = width ; run;
The LOGISTIC ProcedureModel Information Data Set WORK.GROUPED Response Variable (Events) satell Response Variable (Trials) cases Number of Observations 8 Link Function Logit Optimization Technique Fisher’s scoring Response Profile
Ordered Binary Total Value Outcome Frequency 1 Event 111 2 Nonevent 62 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics
Intercept Intercept and Criterion Only Covariates AIC 227.759 201.694 SC 230.912 208.001 -2 Log L 225.759 197.694 Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq Likelihood Ratio 28.0644 1 <.0001 Score 25.6828 1 <.0001 Wald 22.2312 1 <.0001 Analysis of Maximum Likelihood Estimates
Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -11.5128 2.5488 20.4031 <.0001 width 1 0.4646 0.0985 22.2312 <.0001
The LOGISTIC Procedure
Odds Ratio Estimates
Point 95% Wald Effect Estimate Confidence Limits width 1.591 1.312 1.930 Association of Predicted Probabilities and Observed Responses Percent Concordant 66.3 Somers’ D 0.454 Percent Discordant 20.9 Gamma 0.520 Percent Tied 12.8 Tau-a 0.210 Pairs 6882 c 0.727
Table 5.3, p. 116.
Note: The influence option in the model statement provides the deviance residual, the diagonal element of the hat matrix, two confidence interval displacement diagnostics (C and CBAR), the change in the Pearson chi-square statistic (DIFCHSQ), and the change in the deviance (DIFDEV). This option was shown for the model using width as a predictor.
data grouped; set grouped; id = _n_; run; proc logistic data = grouped desc noprint; model satell/cases = ; output out=temp1 reschi=pearsona p=pi_hata; run; data temp1; set temp1; keep id Fitted_yesa pearsona; Fitted_yesa= pi_hata*cases; run; proc logistic data = grouped desc; model satell/cases= width /influence; output out=temp2 reschi=pearson p=pi_hat h=h; run; data temp2; set temp2; Fitted_yes=pi_hat*cases; adjres = pearson/sqrt(1-h); keep pearson Fitted_yes adjres cases satell width id pi_hat; run; data combo; merge temp1 temp2; by id; run; proc print data = combo; format width width.; var width cases satell fitted_yesa pearsona Fitted_yes pearson adjres; run;
The LOGISTIC ProcedureModel Information Data Set WORK.GROUPED Response Variable (Events) satell Response Variable (Trials) cases Number of Observations 8 Link Function Logit Optimization Technique Fisher’s scoring Response Profile
Ordered Binary Total Value Outcome Frequency 1 Event 111 2 Nonevent 62 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics
Intercept Intercept and Criterion Only Covariates AIC 227.759 201.694 SC 230.912 208.001 -2 Log L 225.759 197.694 Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq Likelihood Ratio 28.0644 1 <.0001 Score 25.6828 1 <.0001 Wald 22.2312 1 <.0001 Analysis of Maximum Likelihood Estimates
Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -11.5128 2.5488 20.4031 <.0001 width 1 0.4646 0.0985 22.2312 <.0001
The LOGISTIC Procedure
Odds Ratio Estimates
Point 95% Wald Effect Estimate Confidence Limits
width 1.591 1.312 1.930 Association of Predicted Probabilities and Observed Responses Percent Concordant 66.3 Somers’ D 0.454 Percent Discordant 20.9 Gamma 0.520 Percent Tied 12.8 Tau-a 0.210 Pairs 6882 c 0.727
The LOGISTIC Procedure Regression Diagnostics
Pearson Residual Deviance Residual Covariates Case (1 unit = 0.14) (1 unit = 0.18) Number width Value -8 -4 0 2 4 6 8 Value -8 -4 0 2 4 6 8 1 22.6900 0.6901 | | * | 0.6719 | | * | 2 23.8400 -0.8196 | * | | -0.8370 | * | | 3 24.7700 1.1443 | | *| 1.1487 | | * | 4 25.8400 -1.0606 | * | | -1.0485 | * | | 5 26.7900 -0.3772 | * | | -0.3727 | * | | 6 27.7400 0.4272 | | * | 0.4372 | | * | 7 28.6700 -0.3146 | * | | -0.3072 | * | | 8 30.4100 1.0113 | | * | 1.4051 | | *|
Regression Diagnostics
Hat Matrix Diagonal Intercept Case (1 unit = 0.02) DfBeta (1 unit = 0.07) Number Value 0 2 4 6 8 12 16 Value -8 -4 0 2 4 6 8 1 0.3458 | *| 0.5603 | | *| 2 0.2244 | * | -0.3956 | * | | 3 0.2807 | * | 0.4775 | | * | 4 0.2726 | * | -0.0365 | *| | 5 0.1741 | * | 0.0821 | |* | 6 0.2551 | * | -0.2012 | * | | 7 0.2382 | * | 0.1646 | | * | 8 0.2092 | * | -0.5316 |* | |
Regression Diagnostics
Confidence Interval Displacement C width Case DfBeta (1 unit = 0.07) (1 unit = 0.04) Number Value -8 -4 0 2 4 6 8 Value 0 2 4 6 8 12 16 1 -0.5410 |* | | 0.3848 | * | 2 0.3740 | | * | 0.2505 | * | 3 -0.4295 | * | | 0.7102 | *| 4 -0.0150 | * | 0.5794 | * | 5 -0.0935 | *| | 0.0363 | * | 6 0.2149 | | * | 0.0839 | * | 7 -0.1721 | * | | 0.0406 | * | 8 0.5469 | | *| 0.3422 | * |
The LOGISTIC Procedure
Regression Diagnostics
Confidence Interval Displacement CBar Delta Deviance
Case (1 unit = 0.03) (1 unit = 0.14) Number Value 0 2 4 6 8 12 16 Value 0 2 4 6 8 12 16 1 0.2517 | * | 0.7032 | * | 2 0.1943 | * | 0.8948 | * | 3 0.5109 | *| 1.8304 | * | 4 0.4215 | * | 1.5209 | * | 5 0.0300 | * | 0.1689 | * | 6 0.0625 | * | 0.2537 | * | 7 0.0310 | * | 0.1253 | * | 8 0.2706 | * | 2.2448 | *|
Regression Diagnostics
Delta Chi-Square
Case (1 unit = 0.11) Number Value 0 2 4 6 8 12 16 1 0.7280 | * | 2 0.8660 | * | 3 1.8204 | *| 4 1.5464 | * | 5 0.1723 | * | 6 0.2449 | * | 7 0.1300 | * | 8 1.2933 | * | Fitted_ Fitted_ Obs width cases satell yesa pearsona yes pearson adjres
1 <=23.25 14 5 8.9827 -2.21972 3.8473 0.69012 0.85323 2 23.25-24.25 14 4 8.9827 -2.77706 5.4975 -0.81957 -0.93058 3 24.25-25.25 28 17 17.9653 -0.38043 13.9724 1.14434 1.34923 4 25.25-26.25 39 21 25.0231 -1.34344 24.2136 -1.06063 -1.24356 5 26.25-27.25 22 15 14.1156 0.39321 15.7962 -0.37724 -0.41511 6 27.25-28.25 24 20 15.3988 1.95862 19.1604 0.42716 0.49492 7 28.25-29.25 18 15 11.5491 1.69621 15.4644 -0.31464 -0.36050 8 >29.25 14 14 8.9827 2.79639 13.0469 1.01131 1.13725
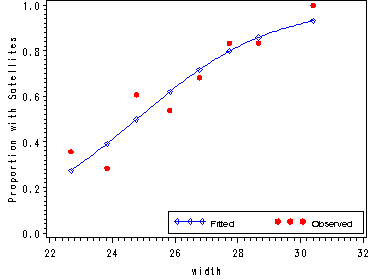
Fig. 5.3, p. 116.
data temp2;
set temp2;
prop = satell/cases;
run;
goption reset = all;
symbol1 v=diamond c=blue h=1 i=spline;
symbol2 v=dot c=red h=.8 i=none;
axis1 order=(0 to 1 by .2) label=(angle=90 'Proportion with Satellites');
axis2 order=(22 to 32 by 2);
legend1 label=none value=(height=1 font=swiss 'Fitted' 'Observed' )
position=(bottom right inside) mode=share cborder=black;
proc gplot data=temp2;
plot (pi_hat prop)*width/ overlay legend=legend1 vaxis=axis1 haxis=axis2;
run;
quit;
goptions reset=all;
Table 5.4, p. 118.
proc logistic data = grouped desc noprint; model satell/cases= ; output out=temp1 difchisq=Pearson_diffa difdev=Likelihood_ratio_diffa; run; data temp1; set temp1; keep id Pearson_diffa Likelihood_ratio_diffa; run; proc logistic data = grouped desc noprint; model satell/cases = width ; output out=temp2 difchisq=Pearson_diff difdev=Likelihood_ratio_diff c=c dfbetas=dfbeta_int dfbeta_width; run; data temp2; set temp2; keep id width Pearson_diff Likelihood_ratio_diff c dfbeta_width; run; data combo; merge temp2 temp1; by id; run; proc print data = combo; format width width.; var width dfbeta_width c Pearson_diff Likelihood_ratio_diff Pearson_diffa Likelihood_ratio_diffa; run;
dfbeta_ Pearson_ Likelihood_ Pearson_ Likelihood_ Obs width width c diff ratio_diff diffa ratio_diffa1 <=23.25 -0.54098 0.38481 0.72800 0.70315 5.36099 5.0931 2 23.25-24.25 0.37397 0.25049 0.86599 0.89483 8.39114 8.0007 3 24.25-25.25 -0.42952 0.71024 1.82042 1.83044 0.17268 0.1708 4 25.25-26.25 -0.01498 0.57945 1.54644 1.52094 2.33013 2.2704 5 26.25-27.25 -0.09352 0.03633 0.17232 0.16890 0.17714 0.1799 6 27.25-28.25 0.21486 0.08387 0.24494 0.25366 4.45410 4.9507 7 28.25-29.25 -0.17208 0.04064 0.12996 0.12534 3.21126 3.5837 8 >29.25 0.54688 0.34220 1.29335 2.24483 8.50836 13.1139
Inputting the aids data, table 5.5, p. 119.
data aids1;
input race1 azt1 symptoms freq race2 azt2 race3 azt3;
cards;
1 1 1 14 0 0 1 1
1 1 0 93 0 0 1 1
1 0 1 32 0 1 1 -1
1 0 0 81 0 1 1 -1
0 1 1 11 1 0 -1 1
0 1 0 52 1 0 -1 1
0 0 1 12 1 1 -1 -1
0 0 0 43 1 1 -1 -1
;
run;
Fitting a Logit model using different dummy and effect coding. In table 5.6, p. 121, the Last=zero column corresponds to the parameter estimates obtained by using dummy variables race1 and azt1. The First=zero column corresponds to the parameter estimates obtained using dummy variables race2 and azt2. The Sum=zero column corresponds to the parameter estimates obtained using the effect coded variables race3 and azt3.
Note: The option descending (desc) in the proc statement so that the lower value, in this case symptoms = zero, is defined as the nonevent.
proc genmod data=aids1 descending; model symptoms = race1 azt1/ dist=bin link=logit; weight freq; run; proc genmod data=aids1 desc; model symptoms = race2 azt2/ dist=bin link=logit; weight freq; run; proc genmod data=aids1 desc; model symptoms = race3 azt3/ dist=bin link=logit; weight freq; run;
The GENMOD ProcedureModel Information
Data Set WORK.AIDS1 Distribution Binomial Link Function Logit Dependent Variable symptoms Scale Weight Variable freq Observations Used 8 Probability Modeled Pr( symptoms = 1 ) Response Profile
Ordered Ordered Level Value Count 1 1 69 2 0 269 Criteria For Assessing Goodness Of Fit
Criterion DF Value Value/DF Deviance 5 335.1512 67.0302 Scaled Deviance 5 335.1512 67.0302 Pearson Chi-Square 5 338.3142 67.6628 Scaled Pearson X2 5 338.3142 67.6628 Log Likelihood -167.5756
Algorithm converged. Analysis Of Parameter Estimates
Standard Wald 95% Confidence Chi- Parameter DF Estimate Error Limits Square Pr > ChiSq Intercept 1 -1.0736 0.2629 -1.5889 -0.5582 16.67 <.0001 race1 1 0.0555 0.2886 -0.5102 0.6212 0.04 0.8476 azt1 1 -0.7195 0.2790 -1.2662 -0.1727 6.65 0.0099 Scale 0 1.0000 0.0000 1.0000 1.0000 NOTE: The scale parameter was held fixed.
The GENMOD Procedure
Model Information Data Set WORK.AIDS1 Distribution Binomial Link Function Logit Dependent Variable symptoms Scale Weight Variable freq Observations Used 8 Probability Modeled Pr( symptoms = 1 ) Response Profile
Ordered Ordered Level Value Count 1 1 69 2 0 269 Criteria For Assessing Goodness Of Fit
Criterion DF Value Value/DF Deviance 5 335.1512 67.0302 Scaled Deviance 5 335.1512 67.0302 Pearson Chi-Square 5 338.3142 67.6628 Scaled Pearson X2 5 338.3142 67.6628 Log Likelihood -167.5756
Algorithm converged. Analysis Of Parameter Estimates
Standard Wald 95% Confidence Chi- Parameter DF Estimate Error Limits Square Pr > ChiSq Intercept 1 -1.7375 0.2404 -2.2087 -1.2664 52.25 <.0001 race2 1 -0.0555 0.2886 -0.6212 0.5102 0.04 0.8476 azt2 1 0.7195 0.2790 0.1727 1.2662 6.65 0.0099 Scale 0 1.0000 0.0000 1.0000 1.0000 NOTE: The scale parameter was held fixed.
The GENMOD Procedure
Model Information Data Set WORK.AIDS1 Distribution Binomial Link Function Logit Dependent Variable symptoms Scale Weight Variable freq Observations Used 8 Probability Modeled Pr( symptoms = 1 ) Response Profile
Ordered Ordered Level Value Count 1 1 69 2 0 269 Criteria For Assessing Goodness Of Fit
Criterion DF Value Value/DF Deviance 5 335.1512 67.0302 Scaled Deviance 5 335.1512 67.0302 Pearson Chi-Square 5 338.3142 67.6628 Scaled Pearson X2 5 338.3142 67.6628 Log Likelihood -167.5756
Algorithm converged. Analysis Of Parameter Estimates
Standard Wald 95% Confidence Chi- Parameter DF Estimate Error Limits Square Pr > ChiSq Intercept 1 -1.4056 0.1467 -1.6931 -1.1181 91.82 <.0001 race3 1 0.0277 0.1443 -0.2551 0.3106 0.04 0.8476 azt3 1 -0.3597 0.1395 -0.6331 -0.0863 6.65 0.0099 Scale 0 1.0000 0.0000 1.0000 1.0000 NOTE: The scale parameter was held fixed.
Inputting the aids data and fitting a logit model using the code in Table A.9, p. 272.
Note: The parameter estimates from the first model corresponds to the column labeled Last=zero and the estimated from the second model corresponds to the column labeled First=zero.
data aids; input race $ azt $ yes no @@; cases = yes + no; cards; white y 14 93 white n 32 81 black y 11 52 black n 12 43 ; run; proc genmod data=aids order=data; class race azt; model yes/cases = race azt / dist=bin link=logit obstats type3; run; proc genmod data = aids desc; class race azt; model yes/cases = race azt/ dist=bin link=logit; run;
The GENMOD ProcedureModel Information Data Set WORK.AIDS Distribution Binomial Link Function Logit Response Variable (Events) yes Response Variable (Trials) cases Observations Used 4 Number Of Events 69 Number Of Trials 338 Class Level Information
Class Levels Values race 2 white black azt 2 y n Criteria For Assessing Goodness Of Fit
Criterion DF Value Value/DF Deviance 1 1.3835 1.3835 Scaled Deviance 1 1.3835 1.3835 Pearson Chi-Square 1 1.3910 1.3910 Scaled Pearson X2 1 1.3910 1.3910 Log Likelihood -167.5756
Algorithm converged. Analysis Of Parameter Estimates
Standard Wald 95% Confidence Chi- Parameter DF Estimate Error Limits Square Pr > ChiSq Intercept 1 -1.0736 0.2629 -1.5889 -0.5582 16.67 <.0001 race white 1 0.0555 0.2886 -0.5102 0.6212 0.04 0.8476 race black 0 0.0000 0.0000 0.0000 0.0000 . . azt y 1 -0.7195 0.2790 -1.2662 -0.1727 6.65 0.0099 azt n 0 0.0000 0.0000 0.0000 0.0000 . . Scale 0 1.0000 0.0000 1.0000 1.0000 NOTE: The scale parameter was held fixed.
The GENMOD Procedure
LR Statistics For Type 3 Analysis
Chi- Source DF Square Pr > ChiSq race 1 0.04 0.8473 azt 1 6.87 0.0088 Observation Statistics
Observation yes cases race azt Pred Xbeta Std HessWgt Lower Upper Resraw Reschi Resdev StResdev StReschi Reslik 1 14 107 white y 0.1496245 -1.737549 0.2403848 13.614362 0.0989724 0.2198735 -2.009824 -0.544703 -0.554665 -1.200988 -1.179418 -1.184051 2 32 113 white n 0.2653998 -1.018089 0.1985145 22.03079 0.1966808 0.3477355 2.009824 0.4281964 0.4252503 1.171303 1.1794176 1.1783512 3 11 63 black y 0.1427012 -1.793034 0.2843628 7.707267 0.087036 0.2251866 2.009824 0.7239488 0.7034699 1.1460546 1.1794176 1.1669593 4 12 55 black n 0.2547241 -1.073574 0.2629407 10.441185 0.1695348 0.3639596 -2.009824 -0.62199 -0.63259 -1.199517 -1.179418 -1.185042 The GENMOD Procedure
Model Information Data Set WORK.AIDS Distribution Binomial Link Function Logit Response Variable (Events) yes Response Variable (Trials) cases Observations Used 4 Number Of Events 69 Number Of Trials 338 Class Level Information
Class Levels Values race 2 black white azt 2 n y Criteria For Assessing Goodness Of Fit
Criterion DF Value Value/DF Deviance 1 1.3835 1.3835 Scaled Deviance 1 1.3835 1.3835 Pearson Chi-Square 1 1.3910 1.3910 Scaled Pearson X2 1 1.3910 1.3910 Log Likelihood -167.5756
Algorithm converged. Analysis Of Parameter Estimates
Standard Wald 95% Confidence Chi- Parameter DF Estimate Error Limits Square Pr > ChiSq Intercept 1 -1.7375 0.2404 -2.2087 -1.2664 52.25 <.0001 race black 1 -0.0555 0.2886 -0.6212 0.5102 0.04 0.8476 race white 0 0.0000 0.0000 0.0000 0.0000 . . azt n 1 0.7195 0.2790 0.1727 1.2662 6.65 0.0099 azt y 0 0.0000 0.0000 0.0000 0.0000 . . Scale 0 1.0000 0.0000 1.0000 1.0000 NOTE: The scale parameter was held fixed.
Results from the logistic model with width and dummy variables for the categorical variable color as predictors. In order generate the predicted probabilities at the bottom of p. 123 two new observations were added to the dataset.
data dummy; if _n_=1 then do; width=26.3; c1=1; c2=0; c3=0; output; width=26.3; c1=0; c2=0; c3=0; output; end; set crab; c1 = 0; if color=1 then c1=1; c2 = 0; if color=2 then c2=1; c3 = 0; if color=3 then c3=1; output; run; proc logistic data = dummy desc; model y = c1 c2 c3 width; output out=temp p=pi_hat; run; proc print data = temp; where y=.; var width c1 c2 c3 pi_hat; run;
The LOGISTIC ProcedureModel Information Data Set WORK.DUMMY Response Variable y Number of Response Levels 2 Number of Observations 173 Link Function Logit Optimization Technique Fisher’s scoring Response Profile
Ordered Total Value y Frequency 1 1 111 2 0 62
NOTE: 2 observations were deleted due to missing values for the response or explanatory variables. Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics
Intercept Intercept and Criterion Only Covariates AIC 227.759 197.457 SC 230.912 213.223 -2 Log L 225.759 187.457 Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq Likelihood Ratio 38.3015 4 <.0001 Score 34.3384 4 <.0001 Wald 27.6788 4 <.0001
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -12.7151 2.7618 21.1965 <.0001 c1 1 1.3299 0.8525 2.4335 0.1188 c2 1 1.4023 0.5484 6.5380 0.0106 c3 1 1.1061 0.5921 3.4901 0.0617 width 1 0.4680 0.1055 19.6573 <.0001 Odds Ratio Estimates
Point 95% Wald Effect Estimate Confidence Limits c1 3.781 0.711 20.102 c2 4.065 1.387 11.909 c3 3.023 0.947 9.646 width 1.597 1.298 1.964 Association of Predicted Probabilities and Observed Responses Percent Concordant 76.9 Somers’ D 0.543 Percent Discordant 22.6 Gamma 0.546 Percent Tied 0.5 Tau-a 0.251 Pairs 6882 c 0.771 Obs width c1 c2 c3 pi_hat
1 26.3 1 0 0 0.71546 2 26.3 0 0 0 0.39942
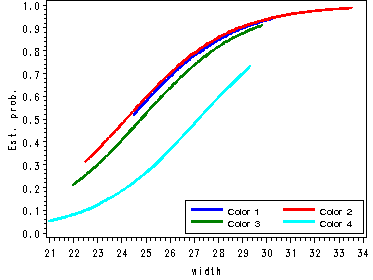
Fig. 5.4, p. 124.
proc sort data=temp;
by width;
run;
data temp1;
set temp;
if c1=1 then pi1 = pi_hat ;
else pi1= . ;
if c2=1 then pi2=pi_hat;
else pi2=.;
if c3=1 then pi3=pi_hat;
else pi3=.;
if c2=0 and c1=0 and c3=0 then pi4=pi_hat;
if c1 = 1 or c2=1 or c3=1 then pi4=.;
run;
goptions reset=all;
symbol1 c=blue i=spline width=2 ;
symbol2 c=red i=spline w=2 ;
symbol3 c=green i=spline w=2 ;
symbol4 c=cyan i=spline w=2 ;
axis1 order=(0 to 1 by .1) label=(angle=90 'Est. prob.');
legend1 label=none value=(height=1 font=swiss 'Color 1' 'Color 2' 'Color 3' 'Color 4' )
position=(bottom right inside) mode=share cborder=black;
proc gplot data=temp1;
plot (pi1 pi2 pi3 pi4)*width/vaxis=axis1 overlay legend=legend1;
run;
quit;
Testing the main effect of color by testing the three dummy variables simultaneously, p. 124.
Note: There are several ways to accomplish this. One way is to add a test statement which uses a Wald Chi-squared test and SAS will provide the test statistic and a p-value. Another way is to run the model with and without the variables to be tested and then take the difference of the -2logL in the Model Fit Statistics table and compare this difference to the Chi-squared distribution with n degrees of freedom (where n=number of variables being tested).
proc logistic data = dummy desc; model y = c1 c2 c3 width; test c1=c2=c3=0; run; proc logistic data = dummy desc; model y=width; run;
The LOGISTIC ProcedureModel Information Data Set WORK.DUMMY Response Variable y Number of Response Levels 2 Number of Observations 173 Link Function Logit Optimization Technique Fisher’s scoring Response Profile
Ordered Total Value y Frequency 1 1 111 2 0 62 NOTE: 2 observations were deleted due to missing values for the response or explanatory variables. Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics
Intercept Intercept and Criterion Only Covariates AIC 227.759 197.457 SC 230.912 213.223 -2 Log L 225.759 187.457 Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq Likelihood Ratio 38.3015 4 <.0001 Score 34.3384 4 <.0001 Wald 27.6788 4 <.0001
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -12.7151 2.7618 21.1965 <.0001 c1 1 1.3299 0.8525 2.4335 0.1188 c2 1 1.4023 0.5484 6.5380 0.0106 c3 1 1.1061 0.5921 3.4901 0.0617 width 1 0.4680 0.1055 19.6573 <.0001 Odds Ratio Estimates
Point 95% Wald Effect Estimate Confidence Limits c1 3.781 0.711 20.102 c2 4.065 1.387 11.909 c3 3.023 0.947 9.646 width 1.597 1.298 1.964 Association of Predicted Probabilities and Observed Responses Percent Concordant 76.9 Somers’ D 0.543 Percent Discordant 22.6 Gamma 0.546 Percent Tied 0.5 Tau-a 0.251 Pairs 6882 c 0.771 Linear Hypotheses Testing Results
Wald Label Chi-Square DF Pr > ChiSq Test 1 6.6246 3 0.0849
The LOGISTIC Procedure
Model Information Data Set WORK.DUMMY Response Variable y Number of Response Levels 2 Number of Observations 173 Link Function Logit Optimization Technique Fisher’s scoring Response Profile
Ordered Total Value y Frequency 1 1 111 2 0 62 NOTE: 2 observations were deleted due to missing values for the response or explanatory variables. Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics
Intercept Intercept and Criterion Only Covariates AIC 227.759 198.453 SC 230.912 204.759 -2 Log L 225.759 194.453 Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq Likelihood Ratio 31.3059 1 <.0001 Score 27.8752 1 <.0001 Wald 23.8872 1 <.0001
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -12.3508 2.6287 22.0749 <.0001 width 1 0.4972 0.1017 23.8872 <.0001 Odds Ratio Estimates
Point 95% Wald Effect Estimate Confidence Limits width 1.644 1.347 2.007 Association of Predicted Probabilities and Observed Responses Percent Concordant 73.5 Somers’ D 0.485 Percent Discordant 25.0 Gamma 0.492 Percent Tied 1.5 Tau-a 0.224 Pairs 6882 c 0.742
Estimating the main effects with Crab data, table 5.7, p. 127.
Note: The type3 option tells SAS to test the main effects as well as the dummy variables for the categorical variables.
proc genmod data = crab desc; class color spine ; model y = color spine width weight/ dist=bin link=logit type3; run;
The GENMOD ProcedureModel Information Data Set WORK.CRAB Distribution Binomial Link Function Logit Dependent Variable y Observations Used 173 Probability Modeled Pr( y = 1 ) Class Level Information
Class Levels Values color 4 1 2 3 4 spine 3 1 2 3 Response Profile
Ordered Ordered Level Value Count 1 1 111 2 0 62 Criteria For Assessing Goodness Of Fit
Criterion DF Value Value/DF Deviance 165 185.2020 1.1224 Scaled Deviance 165 185.2020 1.1224 Pearson Chi-Square 165 169.7557 1.0288 Scaled Pearson X2 165 169.7557 1.0288 Log Likelihood -92.6010
Algorithm converged. Analysis Of Parameter Estimates
Standard Wald 95% Confidence Chi- Parameter DF Estimate Error Limits Square Pr > ChiSq Intercept 1 -9.2734 3.8378 -16.7954 -1.7514 5.84 0.0157 color 1 1 1.6087 0.9355 -0.2250 3.4423 2.96 0.0855 color 2 1 1.5058 0.5667 0.3951 2.6164 7.06 0.0079 color 3 1 1.1198 0.5933 -0.0430 2.2826 3.56 0.0591 color 4 0 0.0000 0.0000 0.0000 0.0000 . . spine 1 1 -0.4003 0.5027 -1.3856 0.5850 0.63 0.4259
The GENMOD Procedure
Analysis Of Parameter Estimates
Standard Wald 95% Confidence Chi- Parameter DF Estimate Error Limits Square Pr > ChiSq
spine 2 1 -0.4963 0.6292 -1.7294 0.7369 0.62 0.4302 spine 3 0 0.0000 0.0000 0.0000 0.0000 . . width 1 0.2631 0.1953 -0.1197 0.6459 1.82 0.1779 weight 1 0.8258 0.7038 -0.5537 2.2053 1.38 0.2407 Scale 0 1.0000 0.0000 1.0000 1.0000 NOTE: The scale parameter was held fixed. LR Statistics For Type 3 Analysis
Chi- Source DF Square Pr > ChiSq color 3 7.60 0.0551 spine 2 1.01 0.6038 width 1 1.80 0.1801 weight 1 1.41 0.2351
Obtaining the same results using dummy variables and proc logistic.
Note: Only proc logistic will provide the likelihood-ratio test comparing the full model to the null model.
data main; set crab; c1 = 0; if color=1 then c1=1; c2 = 0; if color=2 then c2=1; c3 = 0; if color=3 then c3=1; spine1=0; if spine=1 then spine1=1; spine2=0; if spine=2 then spine2=1; run; proc logistic data = main desc; model y = c1 c2 c3 spine1 spine2 width weight; test c1=c2=c3=0; test spine1=spine2=0; run;
The LOGISTIC ProcedureModel Information Data Set WORK.MAIN Response Variable y Number of Response Levels 2 Number of Observations 173 Link Function Logit Optimization Technique Fisher’s scoring Response Profile
Ordered Total Value y Frequency 1 1 111 2 0 62 Model Convergence Status Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics
Intercept Intercept and Criterion Only Covariates AIC 227.759 201.202 SC 230.912 226.428 -2 Log L 225.759 185.202 Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq Likelihood Ratio 40.5565 7 <.0001 Score 36.3068 7 <.0001 Wald 29.4763 7 0.0001
The LOGISTIC Procedure
Analysis of Maximum Likelihood Estimates
Standard Parameter DF Estimate Error Chi-Square Pr > ChiSq Intercept 1 -9.2734 3.8378 5.8386 0.0157 c1 1 1.6087 0.9355 2.9567 0.0855 c2 1 1.5058 0.5667 7.0607 0.0079 c3 1 1.1198 0.5933 3.5624 0.0591 spine1 1 -0.4003 0.5027 0.6340 0.4259 spine2 1 -0.4963 0.6292 0.6222 0.4302 width 1 0.2631 0.1953 1.8152 0.1779 weight 1 0.8258 0.7038 1.3765 0.2407 Odds Ratio Estimates
Point 95% Wald Effect Estimate Confidence Limits c1 4.996 0.799 31.259 c2 4.508 1.485 13.687 c3 3.064 0.958 9.803 spine1 0.670 0.250 1.795 spine2 0.609 0.177 2.089 width 1.301 0.887 1.908 weight 2.284 0.575 9.073 Association of Predicted Probabilities and Observed Responses Percent Concordant 77.6 Somers’ D 0.555 Percent Discordant 22.1 Gamma 0.557 Percent Tied 0.3 Tau-a 0.257 Pairs 6882 c 0.778 Linear Hypotheses Testing Results
Wald Label Chi-Square DF Pr > ChiSq Test 1 7.1610 3 0.0669 Test 2 1.0105 2 0.6034
The first four rows of the deviance and df columns of table 5.8, p. 128.
ods listing close; proc genmod data=crab desc ; class color spine; model y = color|spine|width / dist=bin link=logit type3; ods output modelfit=temp; run; proc genmod data=crab desc; class color spine; model y = color|spine|width@2 / dist=bin link=logit type3; ods output modelfit=temp1; run; proc genmod data=crab desc; class color spine; model y = color spine width color*spine spine*width / dist=bin link=logit type3; ods output modelfit=temp2; run; proc genmod data=crab desc; class color spine; model y = color spine width color*width spine*width / dist=bin link=logit type3; ods output modelfit=temp3; run; ods output close; ods listing; data combo; set temp temp1 temp2 temp3; run; proc print data = combo; where Criterion='Deviance'; var criterion df value; run;
>Obs Criterion DF Value1 Deviance 152 170.4404 6 Deviance 155 173.6738 11 Deviance 158 177.3357 16 Deviance 161 181.5588
The Diarrhea Example:
data diarrhea;
input cep age stay case count;
datalines;
0 0 0 0 385
0 0 1 5 233
0 1 0 3 789
0 1 1 47 1081
1 1 1 5 5
;
run;
proc logistic data = diarrhea descending exactonly;
model case/count = age stay cep;
exact 'parm' age stay cep /estimate = parm;
run;
The LOGISTIC Procedure
Model Information
Data Set WORK.DIARRHEA
Response Variable (Events) case
Response Variable (Trials) count
Number of Observations 5
Model binary logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Binary Total
Value Outcome Frequency
1 Event 60
2 Nonevent 2433
Exact Conditional Analysis
Conditional Exact Tests for 'parm'
--- p-Value ---
Effect Test Statistic Exact Mid
age Score 3.4067 0.0750 0.0624
Probability 0.0252 0.0750 0.0624
stay Score 34.4965 <.0001 <.0001
Probability 9.03E-11 <.0001 <.0001
cep Score 98.8190 <.0001 <.0001
Probability 2.19E-7 <.0001 <.0001
Exact Parameter Estimates for 'parm'
95% Confidence
Parameter Estimate Limits p-Value
age 0.8514 -0.0782 2.0300 0.0800
stay 2.6775 1.5411 4.2937 <.0001
cep 4.9592* 2.9497 Infinity <.0001
NOTE: * indicates a median unbiased estimate.