8.1 Logit Models for Nominal Responses
8.1.2 Alligator Food Choice Example
data gator; input length choice $ @@; cards; 1.24 I 1.30 I 1.30 I 1.32 F 1.32 F 1.40 F 1.42 I 1.42 F 1.45 I 1.45 O 1.47 I 1.47 F 1.50 I 1.52 I 1.55 I 1.60 I 1.63 I 1.65 O 1.65 I 1.65 F 1.65 F 1.68 F 1.70 I 1.73 O 1.78 I 1.78 I 1.78 O 1.80 I 1.80 F 1.85 F 1.88 I 1.93 I 1.98 I 2.03 F 2.03 F 2.16 F 2.26 F 2.31 F 2.31 F 2.36 F 2.36 F 2.39 F 2.41 F 2.44 F 2.46 F 2.56 O 2.67 F 2.72 I 2.79 F 2.84 F 3.25 O 3.28 O 3.33 F 3.56 F 3.58 F 3.66 F 3.68 O 3.71 F 3.89 F ; run;
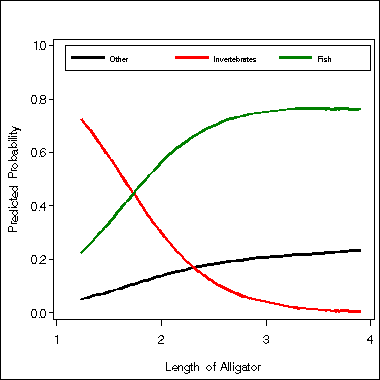
Table 8.2 on parameter estimates and Figure 8.1. Proc logistic of SAS 8.2 handles generalized logits model very nicely. The option link=glogit specifies that the model is generalized logit model. The option aggregate in the model statement requests a test on the global effect of variable length. In order to produce Figure 8.1, we need to generate predicted probabilities. This is accomplished by using output statement. Figure 8.1 is created using proc gplot.
proc logistic data=gator descending ;
model choice (REFERENCE="O") = length / link=glogit scale=none aggregate;
output out = prob PREDPROBS=I;
run;
axis1 label=(a = 90 "Predicted Probability") order = (0 to 1 by .2) minor=none;
axis2 label=("Length of Alligator") order = (1 to 4 by 1) minor = none;
legend1 label=none value=(h=2 font=swiss 'Other' 'Invertebrates' 'Fish')
position=(top right inside) mode=share cborder=black;
symbol i = join w=2;
proc gplot data = prob;
plot (ip_o ip_i ip_f)*length /overlay vaxis=axis1 haxis=axis2 legend=legend1;
run;
quit;
The LOGISTIC Procedure
Model Information
Data Set WORK.GATOR
Response Variable choice
Number of Response Levels 3
Number of Observations 59
Model generalized logit
Optimization Technique Fisher's scoring
Response Profile
Ordered Total
Value choice Frequency
1 O 8
2 I 20
3 F 31
Logits modeled use choice='O' as the reference category.
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Deviance and Pearson Goodness-of-Fit Statistics
Criterion DF Value Value/DF Pr > ChiSq
Deviance 86 75.1140 0.8734 0.7929
Pearson 86 80.1879 0.9324 0.6563
Number of unique profiles: 45
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 119.142 106.341
SC 123.297 114.651
-2 Log L 115.142 98.341
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 16.8006 2 0.0002
Score 12.5702 2 0.0019
Wald 8.9360 2 0.0115
Type III Analysis of Effects
Wald
Effect DF Chi-Square Pr > ChiSq
length 2 8.9360 0.0115
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter choice DF Estimate Error Chi-Square Pr > ChiSq
Intercept I 1 5.6974 1.7938 10.0881 0.0015
Intercept F 1 1.6177 1.3073 1.5314 0.2159
length I 1 -2.4654 0.8997 7.5101 0.0061
length F 1 -0.1101 0.5171 0.0453 0.8314
Odds Ratio Estimates
Point 95% Wald
Effect choice Estimate Confidence Limits
length I 0.085 0.015 0.496
length F 0.896 0.325 2.468
Notice that the same parameter estimates can also be obtained by using proc catmod. We show the code here.
proc catmod data=gator; response logits; direct length; model choice = length ; run; quit;
8.1.4 Belief in Afterlife Example
data afterlife; input race gender belief count; datalines; 1 1 1 371 1 1 2 49 1 1 3 74 1 0 1 250 1 0 2 45 1 0 3 71 0 1 1 64 0 1 2 9 0 1 3 15 0 0 1 25 0 0 2 5 0 0 3 13 ; run;
Table 8.4, Table 8.5 and Table 8.3. After generating the probabilities, we then generate the predicted counts. That is why Table 8.3 comes last.
proc logistic data = afterlife descending;
weight count;
model belief (reference="3") = race gender /link=glogit scale = none aggregate;
output out = prob PREDPROBS=I;
run;
The LOGISTIC Procedure
Type III Analysis of Effects
Wald
Effect DF Chi-Square Pr > ChiSq
race 2 2.0824 0.3530
gender 2 7.2074 0.0272
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter belief DF Estimate Error Chi-Square Pr > ChiSq
Intercept 2 1 -0.7582 0.3614 4.4031 0.0359
Intercept 1 1 0.8828 0.2426 13.2390 0.0003
race 2 1 0.2712 0.3541 0.5863 0.4438
race 1 1 0.3420 0.2370 2.0814 0.1491
gender 2 1 0.1051 0.2465 0.1817 0.6699
gender 1 1 0.4186 0.1713 5.9737 0.0145
proc freq data = prob ; format ip_1-ip_3 f4.2; weight count; tables race*gender*ip_1*ip_2*ip_3/list nocum nopercent out=test ; run;
The FREQ Procedure race gender IP_1 IP_2 IP_3 Frequency --------------------------------------------------- 0 0 0.62 0.12 0.26 43 0 1 0.71 0.10 0.19 88 1 0 0.68 0.12 0.20 366 1 1 0.75 0.10 0.15 494
data table8_3; set test; array p(3) ip_1-ip_3; array pre_count(3); do i = 1 to 3; pre_count(i) = count*p(i); end; drop ip_1-ip_3 i percent; run; proc print data = table8_3 noobs; run;
pre_ pre_ pre_ race gender COUNT count1 count2 count3 0 0 43 26.752 5.1837 11.0648 0 1 88 62.244 8.7615 16.9401 1 0 366 248.245 44.1218 72.9396 1 1 494 372.751 49.1838 72.064
8.2 Cumulative Logit Models for Ordinal Responses
8.2.2 Political Ideology Example
Table 8.6 and parameter estimates.
data ideology;
input party ideology count @@;
cards;
1 1 80 1 2 81 1 3 171 1 4 41 1 5 55
0 1 30 0 2 46 0 3 148 0 4 84 0 5 99
;
proc logistic data = ideology order=data descending;
class party /param = ref;
freq count;
model ideology = party /link=clogit scale=none ;
output out = prob PREDPROBS=I;
run;
proc freq data = prob noprint;
weight count;
tables party*ip_1*ip_2*ip_3*ip_4*ip_5
/list nocum nopercent out=test ;
run;
data table8_6;
set test;
array p(5) ip_1-ip_5;
array pcount(5);
do i = 1 to 5;
pcount(i) = count*p(i);
end;
drop ip_1-ip_5 i percent;
run;
proc print data = table8_6 noobs;
run;
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 58.6451 1 <.0001
Score 57.2448 1 <.0001
Wald 57.0182 1 <.0001
Type III Analysis of Effects
Wald
Effect DF Chi-Square Pr > ChiSq
party 1 57.0182 <.0001
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 5 1 -2.0440 0.1188 295.9293 <.0001
Intercept 4 1 -1.2116 0.1031 138.0265 <.0001
Intercept 3 1 0.5000 0.0943 28.1405 <.0001
Intercept 2 1 1.4945 0.1134 173.6781 <.0001
party 0 1 0.9745 0.1291 57.0182 <.0001
Odds Ratio Estimates
Point 95% Wald
Effect Estimate Confidence Limits
party 0 vs 1 2.650 2.058 3.412
party COUNT pcount1 pcount2 pcount3 pcount4 pcount5
0 407 31.7714 44.0346 151.708 75.5005 103.985
1 428 78.4308 83.1523 168.226 49.1170 49.074
8.2.3 Invariance to Choice of Response Categories
8.2.2 Political Ideology Example
Result in this section.
data ideology1; set ideology; if ideology = 1 or ideology = 2 then ideo = 1; else if ideology = 4 or ideology = 5 then ideo = 3; else ideo = 2; run; proc logistic data = ideology1 order=data descending; class party /param = ref; freq count; model ideo = party /link=clogit scale=none ; run;
The LOGISTIC Procedure
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 1826.542 1768.834
SC 1835.997 1783.016
-2 Log L 1822.542 1762.834
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 59.7085 1 <.0001
Score 58.5204 1 <.0001
Wald 57.9280 1 <.0001
Type III Analysis of Effects
Wald
Effect DF Chi-Square Pr > ChiSq
party 1 57.9280 <.0001
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 3 1 -1.2195 0.1041 137.1879 <.0001
Intercept 2 1 0.4931 0.0951 26.8774 <.0001
party 0 1 1.0059 0.1322 57.9280 <.0001
8.3 Paired-Category Logits for Ordinal Responses
8.3.2 Political Ideology Example Revisited
SAS proc catmod is the procedure to use for adjacent-categories logit models. Here is the syntax for a general adjacent-categories logit model. The response statement below specifies that the model is adjacent-categories logit model.
proc catmod data = ideology; weight count; response alogits; model ideology = party; run; quit;
The syntax for the simpler adjacent-categories model (8.3.2) on page 216 is slightly different. Here is a simple way of doing it. The _RESPONSE_ keyword allows modeling the levels of ideology. The coding for variable party uses simple coding scheme.
proc catmod data = ideology; weight count; response alogits; model ideology = _response_ party ; run; quit;
If we want to dummy code the variable party, we can specify the design matrix directly as in the following example. Notice the sign difference of parameter estimate for variable party from the book on page 217. This is because our party is coded in the opposite way from the book.
proc catmod data = ideology ;
weight count;
population party;
response alogits;
model ideology = (1 0 0 0 0,
0 1 0 0 0,
0 0 1 0 0,
0 0 0 1 0,
1 0 0 0 1,
0 1 0 0 1,
0 0 1 0 1,
0 0 0 1 1)
(1='Group2/1', 2='Group3/2', 3='Group4/3', 4='Group5/4', 5='party');
run;
quit;
The CATMOD Procedure
Data Summary
Response ideology Response Levels 5
Weight Variable count Populations 2
Data Set IDEOLOGY Total Frequency 835
Frequency Missing 0 Observations 10
Population Profiles
Sample party Sample Size
------------------------------
1 0 407
2 1 428
Response Profiles
Response ideology
--------------------
1 1
2 2
3 3
4 4
5 5
Response Functions and Design Matrix
Function Response Design Matrix
Sample Number Function 1 2 3 4 5
-----------------------------------------------------------------------------
1 1 0.42744 1 0 0 0 0
2 1.16857 0 1 0 0 0
3 -0.56640 0 0 1 0 0
4 0.16430 0 0 0 1 0
2 1 0.01242 1 0 0 0 1
2 0.74721 0 1 0 0 1
3 -1.42809 0 0 1 0 1
4 0.29376 0 0 0 1 1
Analysis of Variance
Source DF Chi-Square Pr > ChiSq
------------------------------------------
Group2/1 1 9.82 0.0017
Group3/2 1 109.13 <.0001
Group4/3 1 43.44 <.0001
Group5/4 1 8.32 0.0039
party 1 52.63 <.0001
Residual 3 5.38 0.1459
Analysis of Weighted Least Squares Estimates
Standard Chi-
Effect Parameter Estimate Error Square Pr > ChiSq
--------------------------------------------------------------------
Model 1 0.4368 0.1394 9.82 0.0017
2 1.1710 0.1121 109.13 <.0001
3 -0.7161 0.1087 43.44 <.0001
4 0.3534 0.1225 8.32 0.0039
5 -0.4318 0.0595 52.63 <.0001
8.3.4 Continuation-Ratio Logits
We will use proc catmod in this section. In proc catmod, we can specify the response function using the response statement. Also, we need to pad empty cells in order for proc catmod to perform the parameter estimation successfully. This can be done using option addcell in the model statement.
data toxicity;
input con r count;
cards;
0 1 15
0 2 1
0 3 281
62.5 1 17
62.5 2 0
62.5 3 225
125 1 22
125 2 7
125 3 283
250 1 38
250 2 59
250 3 202
500 1 144
500 2 132
500 3 9
;
run;
proc catmod data = toxicity;
weight count;
direct con;
response 0 1 -1,
1 -.5 -.5 log;
model r = con /addcell=.0005;
run;
quit;
The CATMOD Procedure
Analysis of Weighted Least Squares Estimates
Function Standard Chi-
Parameter Number Estimate Error Square Pr > ChiSq
-------------------------------------------------------------------
Intercept 1 -4.4392 0.3101 204.99 <.0001
2 -1.4280 0.1904 56.26 <.0001
con 1 0.0124 0.00103 144.60 <.0001
2 0.00455 0.000499 83.22 <.0001