Table 11.1 and Table 11.2 on page 194.
data table11_1; input Subject Group $ week1-week8; datalines; 1 A 45 45 45 45 80 80 80 90 2 A 20 25 25 25 30 35 30 50 3 A 50 50 55 70 70 75 90 90 4 A 25 25 35 40 60 60 70 80 5 A 100 100 100 100 100 100 100 100 6 A 20 20 30 50 50 60 85 95 7 A 30 35 35 40 50 60 75 85 8 A 30 35 45 50 55 65 65 70 9 B 40 55 60 70 80 85 90 90 10 B 65 65 70 70 80 80 80 80 11 B 30 30 40 45 65 85 85 85 12 B 25 35 35 35 40 45 45 45 13 B 45 45 80 80 80 80 80 80 14 B 15 15 10 10 10 20 20 20 15 B 35 35 35 45 45 45 50 50 16 B 40 40 40 55 55 55 60 65 17 C 20 20 30 30 30 30 30 30 18 C 35 35 35 40 40 40 40 40 19 C 35 35 35 40 40 40 45 45 20 C 45 65 65 65 80 85 95 100 21 C 45 65 70 90 90 95 95 100 22 C 25 30 30 35 40 40 40 40 23 C 25 25 30 30 30 30 35 40 24 C 15 35 35 35 40 50 65 65 ; run; options linesize = 100; proc corr data = table11_1 nosimple noprob; var week:; run;
Pearson Correlation Coefficients, N = 24
week1 week2 week3 week4 week5 week6 week7 week8
week1 1.00000 0.92804 0.88202 0.83065 0.79366 0.71256 0.61635 0.55442
week2 0.92804 1.00000 0.92256 0.87741 0.84668 0.78959 0.70415 0.64260
week3 0.88202 0.92256 1.00000 0.95309 0.90921 0.85426 0.76673 0.70079
week4 0.83065 0.87741 0.95309 1.00000 0.92152 0.87863 0.83134 0.77160
week5 0.79366 0.84668 0.90921 0.92152 1.00000 0.97343 0.91495 0.88196
week6 0.71256 0.78959 0.85426 0.87863 0.97343 1.00000 0.95693 0.92669
week7 0.61635 0.70415 0.76673 0.83134 0.91495 0.95693 1.00000 0.97761
week8 0.55442 0.64260 0.70079 0.77160 0.88196 0.92669 0.97761 1.00000
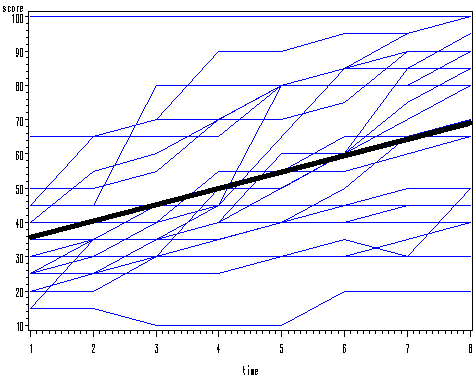
Figure 11.2 on page 195. In order to generate this plot, we need to reshape the data from wide to long format. This is done in a data step. The overall regression line is generated using the regression result in a data step. We merged the original data set and the data set with overall predicted values together before plotting them.
data table11_1long; set table11_1; array week(8) week1-week8; do time = 1 to 8; score = week(time); output; end; drop week1-week8; run; proc reg data = table11_1long ; model score = time; run; quit; data pred; set table11_1long; subject= 100; score = 30.93006 + 4.76438*time; run; data all; set table11_1long pred; run; goptions reset = all; symbol1 i = join v=none r=24 c= blue w=1.5; symbol2 i = join v = none c = black w=4; proc gplot data = all; plot score*time = subject / nolegend; run; quit;
Figure 11.3 on page 195. We created a data set with averaged scores for each group over time using proc sql.
proc sql; create table ave as select distinct mean(score) as score, time as time, group as group from table11_1long group by group, time; quit; symbol1 i = join v= none c = black l = 4; symbol2 i = join v = none c = blue l = 1; symbol3 i = join v = none c = green l = 5; proc gplot data = ave; plot score*time = group; run; quit;
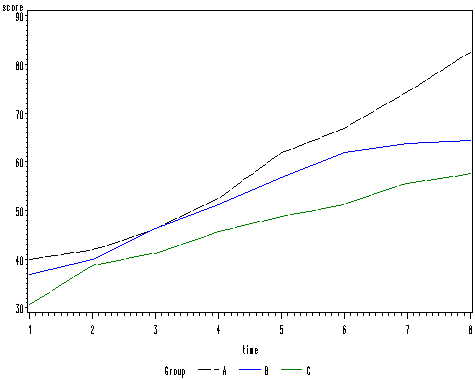
Figure 11.4 on page 196. Proc insight can be used to generate scatter plot matrix.
proc insight data = table11_1 nomenu noconfirm; scatter week1 week2 week3 week4 week5 week6 week7 week8* week1 week2 week3 week4 week5 week6 week7 week8 /markersize=5; run; quit;

Table 11.3 on page 197.
Model (11.1).
data table11_3a; set table11_1long; if group = 'B' then do ; a2 = 1; a3 = 0; end; if group = 'C' then do ; a2 = 0; a3 = 1; end; if group = 'A' then do ; a2 = 0; a3 = 0; end; run; proc reg data = table11_3a; model score = time a2 a3 ; run; quit;
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 36.84152 3.97120 9.28 <.0001
time 1 4.76438 0.66187 7.20 <.0001
a2 1 -5.62500 3.71472 -1.51 0.1316
a3 1 -12.10937 3.71472 -3.26 0.0013
Model (11.2).
proc glm data = table11_3a; model score = time a2 a3 time*a2 time*a3 /solution ss3; run; quit;
Standard Parameter Estimate Error t Value Pr > |t| Intercept 29.82142857 5.77401157 5.16 <.0001 time 6.32440476 1.14342467 5.53 <.0001 a2 3.34821429 8.16568547 0.41 0.6823 a3 -0.02232143 8.16568547 -0.00 0.9978 time*a2 -1.99404762 1.61704668 -1.23 0.2191 time*a3 -2.68601190 1.61704668 -1.66 0.0984
Table 11.4 on page 198.
proc reg data = table11_1long;
by subject;
model score = time;
ods output parameterestimates = table11_4 (keep=subject variable estimate stderr) ;
run;
quit;
proc tabulate data=table11_4 ;
class subject variable /order=data;
var estimate stderr;
table subject='Subject'*sum='',
variable=''*(estimate stderr )
/ RTS=20 row=float;
run;
------------------------------------------------------------------------ | | Intercept | time | | |-------------------------+-------------------------| | | Estimate | StdErr | Estimate | StdErr | |------------------+------------+------------+------------+------------| |Subject | | | | | |------------------| | | | | |1 | 30.00| 7.29| 7.50| 1.44| |------------------+------------+------------+------------+------------| |2 | 15.54| 4.10| 3.21| 0.81| |------------------+------------+------------+------------+------------| |3 | 39.82| 3.21| 6.43| 0.64| |------------------+------------+------------+------------+------------| |4 | 11.61| 3.39| 8.39| 0.67| |------------------+------------+------------+------------+------------| |5 | 100.00| 0.00| 0.00| 0.00| |------------------+------------+------------+------------+------------| |6 | 0.89| 5.30| 11.19| 1.05| |------------------+------------+------------+------------+------------| |7 | 15.36| 4.67| 7.98| 0.92| |------------------+------------+------------+------------+------------| |8 | 25.36| 1.97| 5.89| 0.39| |------------------+------------+------------+------------+------------| |9 | 38.57| 3.52| 7.26| 0.70| |------------------+------------+------------+------------+------------| |10 | 61.96| 2.24| 2.62| 0.44| |------------------+------------+------------+------------+------------| |11 | 14.46| 5.89| 9.70| 1.17| |------------------+------------+------------+------------+------------| |12 | 26.07| 2.15| 2.68| 0.43| |------------------+------------+------------+------------+------------| |13 | 48.75| 8.93| 5.00| 1.77| |------------------+------------+------------+------------+------------| |14 | 10.18| 3.21| 1.07| 0.64| |------------------+------------+------------+------------+------------| |15 | 31.25| 1.95| 2.50| 0.39| |------------------+------------+------------+------------+------------| |16 | 34.11| 2.81| 3.81| 0.56| |------------------+------------+------------+------------+------------| |17 | 21.07| 2.55| 1.43| 0.51| |------------------+------------+------------+------------+------------| |18 | 34.11| 1.16| 0.89| 0.23| |------------------+------------+------------+------------+------------| |19 | 32.14| 1.16| 1.61| 0.23| |------------------+------------+------------+------------+------------| |20 | 42.32| 3.70| 7.26| 0.73| |------------------+------------+------------+------------+------------| |21 | 48.57| 6.14| 7.26| 1.22| |------------------+------------+------------+------------+------------| |22 | 24.82| 1.89| 2.26| 0.37| |------------------+------------+------------+------------+------------| |23 | 22.32| 1.71| 1.85| 0.34| |------------------+------------+------------+------------+------------| |24 | 13.04| 4.49| 6.55| 0.89| ------------------------------------------------------------------------
Table 11.5 on page 198 and table 11.6 on page 199.
proc sql; create table table11_5 as select distinct table11_4.*, x.a2 as a2, x.a3 as a3 from table11_4, table11_3a as x where table11_4.subject = x.subject; quit; proc reg data = table11_5; where variable='Intercept'; model estimate = a2 a3 ; run; quit;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr >
Model 2 60.19080 30.09540 0.07 0.9367
Error 21 9632.53747 458.69226
Corrected Total 23 9692.72826
Root MSE 21.41710 R-Square 0.0062
Dependent Mean 30.93006 Adj R-Sq -0.0884
Coeff Var 69.24365
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 29.82143 7.57209 3.94 0.0008
a2 1 3.34821 10.70855 0.31 0.7576
a3 1 -0.02232 10.70855 -0.00 0.9984
proc reg data = table11_5; where variable='time'; model estimate = a2 a3 ; run; quit;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 2 31.11920 15.55960 1.67 0.2130
Error 21 196.11634 9.33887
Corrected Total 23 227.23554
Root MSE 3.05596 R-Square 0.1369
Dependent Mean 4.76438 Adj R-Sq 0.0548
Coeff Var 64.14169
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 6.32440 1.08044 5.85 <.0001
a2 1 -1.99405 1.52798 -1.31 0.2060
a3 1 -2.68601 1.52798 -1.76 0.0933
Table 11.7 on page 207. Row 1 is model (11.2) shown in Table 11.3. Row 2 is Table 11.5 and Table 11.6 shown above. We will focus on GEE models using proc genmod.
GEE, independent:
proc genmod data = table11_3a; class subject; model score = time a2 a3 time*a2 time*a3 ; repeated subject = subject /type=ind modelse; run; quit;
Analysis Of GEE Parameter Estimates
Model-Based Standard Error Estimates
Standard 95% Confidence
Parameter Estimate Error Limits Z Pr > |Z|
Intercept 29.8214 5.7740 18.5046 41.1383 5.16 <.0001
time 6.3244 1.1434 4.0833 8.5655 5.53 <.0001
a2 3.3482 8.1657 -12.6562 19.3527 0.41 0.6818
a3 -0.0223 8.1657 -16.0268 15.9821 -0.00 0.9978
time*a2 -1.9940 1.6170 -5.1634 1.1753 -1.23 0.2175
time*a3 -2.6860 1.6170 -5.8554 0.4833 -1.66 0.0967
Scale 20.9593 .
GEE, equi-correlated:
proc genmod data = table11_3a; class subject; model score = time a2 a3 time*a2 time*a3 ; repeated subject = subject /type=cs modelse; run; quit;
Analysis Of GEE Parameter Estimates
Model-Based Standard Error Estimates
Standard 95% Confidence
Parameter Estimate Error Limits Z Pr > |Z|
Intercept 29.8214 7.1314 15.8442 43.7986 4.18 <.0001
time 6.3244 0.4958 5.3527 7.2961 12.76 <.0001
a2 3.3482 10.0853 -16.4185 23.1150 0.33 0.7399
a3 -0.0223 10.0853 -19.7891 19.7444 -0.00 0.9982
time*a2 -1.9940 0.7011 -3.3682 -0.6199 -2.84 0.0045
time*a3 -2.6860 0.7011 -4.0602 -1.3119 -3.83 0.0001
Scale 20.9593 .
GEE, AR(1)
proc genmod data = table11_3a; class subject; model score = time a2 a3 time*a2 time*a3 ; repeated subject = subject /type=ar(1) modelse ; run; quit;
Analysis Of GEE Parameter Estimates
Model-Based Standard Error Estimates
Standard 95% Confidence
Parameter Estimate Error Limits Z Pr > |Z|
Intercept 33.5377 7.7190 18.4086 48.6667 4.34 <.0001
time 6.0732 0.7137 4.6744 7.4720 8.51 <.0001
a2 -0.3419 10.9164 -21.7376 21.0538 -0.03 0.9750
a3 -6.4735 10.9164 -27.8692 14.9222 -0.59 0.5532
time*a2 -2.1418 1.0093 -4.1200 -0.1636 -2.12 0.0338
time*a3 -2.2353 1.0093 -4.2135 -0.2571 -2.21 0.0268
Scale 21.0786 .
GEE, unstructured, algorithm does not converge for more than 5000 iterations. The result therefore does not match with the result in the book which was generated using Stata.
proc genmod data = table11_3a; class subject; model score = time a2 a3 time*a2 time*a3 ; repeated subject = subject /type=un modelse maxit=5000 converge=.01; run; quit;
WARNING: Iteration limit exceeded.
Analysis Of GEE Parameter Estimates
Empirical Standard Error Estimates
Standard 95% Confidence
Parameter Estimate Error Limits Z Pr > |Z|
Intercept 34.1561 9.4020 15.7284 52.5837 3.63 0.0003
time 6.2530 1.1736 3.9528 8.5533 5.33 <.0001
a2 -8.4854 10.5225 -29.1091 12.1383 -0.81 0.4200
a3 -6.5443 10.0545 -26.2506 13.1621 -0.65 0.5151
time*a2 -1.3303 1.6162 -4.4979 1.8373 -0.82 0.4104
time*a3 -2.6339 1.4638 -5.5029 0.2351 -1.80 0.0720
Analysis Of GEE Parameter Estimates
Model-Based Standard Error Estimates
Standard 95% Confidence
Parameter Estimate Error Limits Z Pr > |Z|
Intercept 34.1561 6.7387 20.9484 47.3638 5.07 <.0001
time 6.2530 0.0788 6.0986 6.4074 79.37 <.0001
a2 -8.4854 9.5300 -27.1639 10.1931 -0.89 0.3733
a3 -6.5443 9.5300 -25.2228 12.1343 -0.69 0.4923
time*a2 -1.3303 0.1114 -1.5487 -1.1119 -11.94 <.0001
time*a3 -2.6339 0.1114 -2.8523 -2.4155 -23.64 <.0001
Scale 21.3377 .
Random Effects:
proc mixed data = table11_3a method=ml; class subject; model score = time a2 a3 time*a2 time*a3 /solution; random intercept /subject=subject type=un; run;
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 29.8214 7.0468 21 4.23 0.0004
time 6.3244 0.4630 165 13.66 <.0001
a2 3.3482 9.9657 165 0.34 0.7373
a3 -0.02232 9.9657 165 -0.00 0.9982
time*a2 -1.9940 0.6548 165 -3.05 0.0027
time*a3 -2.6860 0.6548 165 -4.10 <.0001