2.2 Examples
Table 2.1 on page 18.
data table2_1; input town country @@; datalines; 0 2 1 0 1 3 0 0 2 0 3 1 0 1 1 1 1 1 1 0 1 0 2 2 0 2 1 0 3 1 0 2 1 0 2 0 1 1 3 1 3 1 4 0 1 2 3 . 2 . 0 . ; run; proc means data = table2_1 n mean std var; var town country; run;
Variable N Mean Std Dev Variance -------------------------------------------------------------- town 26 1.4230769 1.1721118 1.3738462 country 23 0.9130435 0.9001537 0.8102767 --------------------------------------------------------------
Table 2.2 on page 20. In order to use proc genmod to perform our analyses, we have to reshape our data from wide to long. Here is the code for it.
data long; set table2_1; array varname(2) town country; do group = 1 to 2; y = varname(group); output; end; keep y group; run;
A. Model (2.1)
proc genmod data = long; model y = /dist=poisson; output out = overall reschi=reschi; ods output parameterestimates = col2; run; quit; data col2; set col2; theta = exp(estimate); run; proc print data = col2; where parameter = "Intercept"; var theta; run; Obs theta 1 1.18367 proc freq data = overall; tables group*y*reschi /out = model1 list nopercent nocum; format reschi 6.3; run;
The FREQ Procedure
group y reschi Frequency
---------------------------------
1 0 -1.088 6
1 1 -0.169 10
1 2 0.750 4
1 3 1.669 5
1 4 2.589 1
2 0 -1.088 9
2 1 -0.169 8
2 2 0.750 5
2 3 1.669 1
Frequency Missing = 3
B. Model (2.2).
proc sort data = long; by group; run; proc genmod data = long; by group; model y = /dist=poisson; output out = bygroup reschi=reschi; ods output parameterestimates = col3; run; quit; data col3; set col3; theta = exp(estimate); run; proc print data = col3; where parameter ~="Scale"; var theta; run;
Obs theta 1 1.42308 3 0.91304
proc freq data = bygroup; tables group*y*reschi /out=model2 list nopercent nocum; format reschi 6.3; run;
The FREQ Procedure
group y reschi Frequency
---------------------------------
1 0 -1.193 6
1 1 -0.355 10
1 2 0.484 4
1 3 1.322 5
1 4 2.160 1
2 0 -0.956 9
2 1 0.091 8
2 2 1.138 5
2 3 2.184 1
Frequency Missing = 3
Figure 2.1 on page 20. We will use the two data sets created from the previous example.
proc format;
value grp 1 = "town"
2 = "country";
run;
goptions reset=all hsize=6 vsize=2;
axis1 order = (-2 to 3 by 1) minor = none;
axis2 offset = (1, 1) minor=none label=(a=90 r= 0 'model 2.1');
symbol i = needle w=3 value=none;
proc gplot data = model1;
by group;
format group grp.;
plot count*reschi /vaxis = axis2 haxis= axis1 ;
run;
quit;
axis2 offset = (1, 1) minor=none label=(a=90 r= 0 'model 2.2');
proc gplot data = model2;
by group;
format group grp.;
plot count*reschi /vaxis = axis2 haxis= axis1 ;
run;
quit;
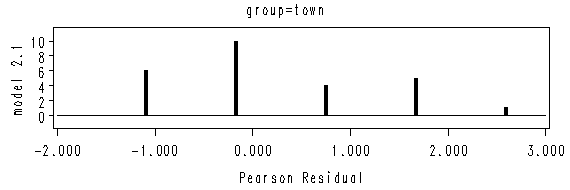
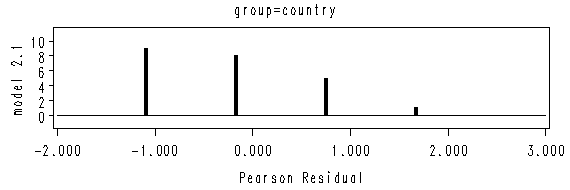
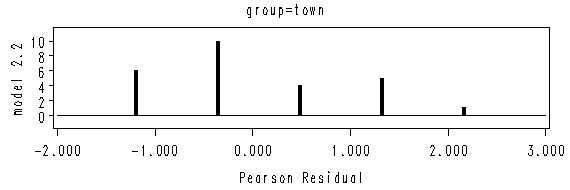
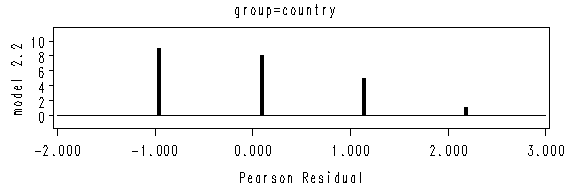
Results on page 21.
For model (2.1):
proc genmod data = long; model y = /dist=poisson; run; quit;
Criteria For Assessing Goodness Of Fit Criterion DF Value Value/DF Deviance 48 56.0335 1.1674 Scaled Deviance 48 56.0335 1.1674 Pearson Chi-Square 48 46.7586 0.9741 Scaled Pearson X2 48 46.7586 0.9741 Log Likelihood -48.2199
For model (2.2):
proc genmod data = long; class group; model y = group/dist=poisson; run; quit;
Criteria For Assessing Goodness Of Fit Criterion DF Value Value/DF Deviance 47 53.3057 1.1342 Scaled Deviance 47 53.3057 1.1342 Pearson Chi-Square 47 43.6589 0.9289 Scaled Pearson X2 47 43.6589 0.9289 Log Likelihood -46.8560
Table 2.3 on page 22.
data table2_3; input bage bweight gage gweight; label bage = "boys gestational age"; label bweight = "boys weight"; label gage = "girls gestational age"; label gweight = "girls weight"; datalines; 40 2968 40 3317 38 2795 36 2729 40 3163 40 2935 35 2925 38 2754 36 2625 42 3210 37 2847 39 2817 41 3292 40 3126 40 3473 37 2539 37 2628 36 2412 38 3176 38 2991 40 3421 39 2875 38 2975 40 3231 ; run; options nolabel; proc means data = table2_3 mean ; run;
The MEANS Procedure Variable Mean ------------------------ bage 38.3333333 bweight 3024.00 gage 38.7500000 gweight 2911.33 ------------------------
Figure 2.2 on page 22.
goptions reset = all;
symbol1 v=circle c=black h=1 ;
symbol2 v = dot c=black h=1;
axis1 order = (2000 to 3500 by 500) label=(a=90 'Birth weight') minor = none;
axis2 order = (34 to 42 by 2) offset = (1, 2) minor = none label=('Gestational Age');
proc gplot data = table2_3;
plot bweight*bage gweight*gage /overlay vaxis=axis1 haxis=axis2;
run;
quit;
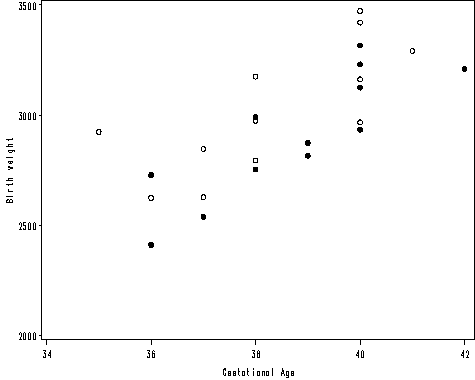
Table 2.4 on page 25. The previous data is in wide format. We need to use the long format of the data to perform regression analysis. Proc reg with option usscp gives the uncorrected sums of squares and cross-products matrix. We also use the by statement to get these for the boys and girls group.
data birthweight; input female age weight; cards; 0 40 2968 0 38 2795 0 40 3163 0 35 2925 0 36 2625 0 37 2847 0 41 3292 0 40 3473 0 37 2628 0 38 3176 0 40 3421 0 38 2975 1 40 3317 1 36 2729 1 40 2935 1 38 2754 1 42 3210 1 39 2817 1 40 3126 1 37 2539 1 36 2412 1 38 2991 1 39 2875 1 40 3231 ; run; proc reg data = birthweight usscp; by female; model weight = age ; run; quit;
female=0
The REG Procedure
Uncorrected Sums of Squares and Crossproducts
Variable Intercept age weight
Intercept 12 460 36288
age 460 17672 1395370
weight 36288 1395370 110623496
female=1
Uncorrected Sums of Squares and Crossproducts
Variable Intercept age weight
Intercept 12 465 34936
age 465 18055 1358497
weight 34936 1358497 102575468
Table 2.5 on page 26.
Model (2.6) where variable female is a predictor variable. The intercept for female group a2 is the difference between the Intercept and the coefficient for female: -1610.28254 + (-163.03930) = -1773.3218.
proc reg data = birthweight usccp;
model weight = age female;
run;
quit;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 2 1171103 585551 18.67 <.0001
Error 21 658771 31370
Corrected Total 23 1829873
Root MSE 177.11588 R-Square 0.6400
Dependent Mean 2967.66667 Adj R-Sq 0.6057
Coeff Var 5.96819
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 -1610.28254 786.07771 -2.05 0.0532
age 1 120.89433 20.46295 5.91 <.0001
female 1 -163.03930 72.80821 -2.24 0.0361
Model (2.7) where we do two separate regression analyses, one on each gender group.
proc reg data = birthweight usccp; by female; model weight = age ; run; quit;
female=0
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 -1268.67241 1239.97381 -1.02 0.3304
age 1 111.98276 32.31174 3.47 0.0061
female=1
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 -2141.66667 1016.04886 -2.11 0.0613
age 1 130.40000 26.19428 4.98 0.0006
We can also think this model in terms of interaction of age and female.
proc glm data = birthweight ; model weight = age female age*female /solution; run; quit;
Standard Parameter Estimate Error t Value Pr > |t| Intercept -1268.672414 1114.638402 -1.14 0.2685 age 111.982759 29.045695 3.86 0.0010 female -872.994253 1611.330856 -0.54 0.5940 age*female 18.417241 41.755817 0.44 0.6639
Table 2.6 on page 26.
proc reg data = birthweight usscp; model weight = age female; output out = mod1 p=p1; run; quit; proc reg data = mod1 usscp; by female; model weight = age ; output out = mod2 p=p2; run; quit; proc print data = mod2 noobs; run;
female age weight p1 p2 0 40 2968 3225.49 3210.64 0 38 2795 2983.70 2986.67 0 40 3163 3225.49 3210.64 0 35 2925 2621.02 2650.72 0 36 2625 2741.91 2762.71 0 37 2847 2862.81 2874.69 0 41 3292 3346.38 3322.62 0 40 3473 3225.49 3210.64 0 37 2628 2862.81 2874.69 0 38 3176 2983.70 2986.67 0 40 3421 3225.49 3210.64 0 38 2975 2983.70 2986.67 1 40 3317 3062.45 3074.33 1 36 2729 2578.87 2552.73 1 40 2935 3062.45 3074.33 1 38 2754 2820.66 2813.53 1 42 3210 3304.24 3335.13 1 39 2817 2941.56 2943.93 1 40 3126 3062.45 3074.33 1 37 2539 2699.77 2683.13 1 36 2412 2578.87 2552.73 1 38 2991 2820.66 2813.53 1 39 2875 2941.56 2943.93 1 40 3231 3062.45 3074.33
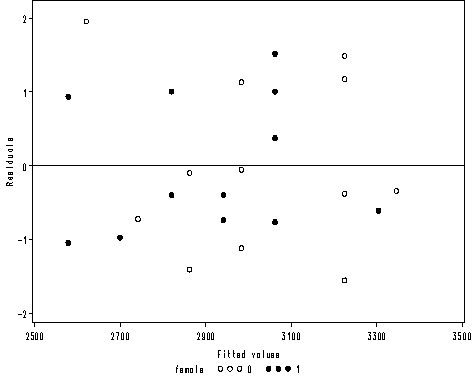
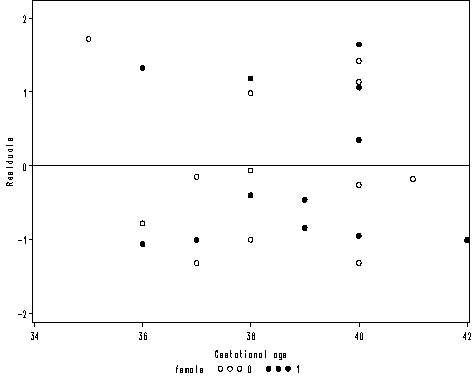
Figure 2.3 on page 27.
symbol1 v=circle c=black h=1 ;
symbol2 v = dot c=black h=1;
axis1 order = (2500 to 3500 by 500) label=('Fitted values') minor = none;
axis2 order = (-2 to 2 by 1) offset = (1, 2) minor = none label=(a=90 'Residuals');
proc gplot data = mod2;
plot r*p1 = female /vaxis=axis2 haxis=axis1 vref=0;
run;
quit;
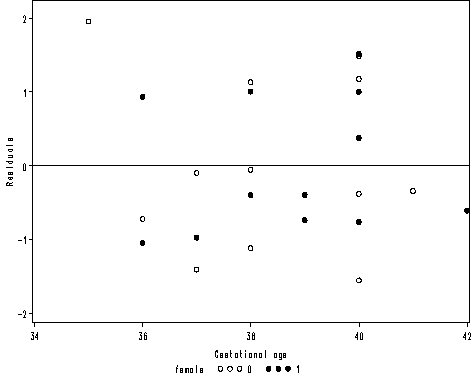
axis1 order = (34 to 42 by 2) label=('Gestational age') minor = none;
axis2 order = (-2 to 2 by 1) offset = (1, 2) minor = none label=(a=90 'Residuals');
proc gplot data = mod2;
plot r*age = female /vaxis=axis2 haxis=axis1 vref=0;
run;
quit;
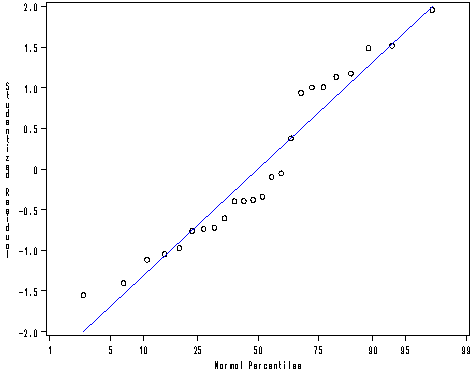
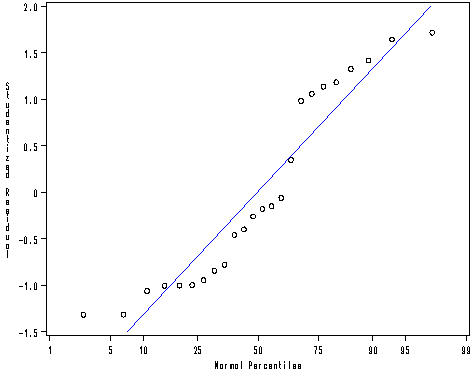
proc univariate data = mod2 noprint; probplot r / normal(mu = est sigma=est color=blue l=1 w=1); run;
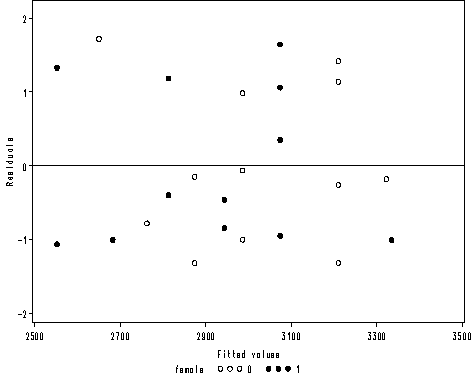
Figure 2.4 on page 28.
symbol1 v=circle c=black h=1 ;
symbol2 v = dot c=black h=1;
axis1 order = (2500 to 3500 by 200) label=('Fitted values') minor = none;
axis2 order = (-2 to 2 by 1) offset = (1, 2) minor = none label=(a=90 'Residuals');
proc gplot data = mod2;
plot r2*p2 = female /vaxis=axis2 haxis=axis1 vref=0;
run;
quit;
axis1 order = (34 to 42 by 2) label=('Gestational age') minor = none;
axis2 order = (-2 to 2 by 1) offset = (1, 2) minor = none label=(a=90 'Residuals');
proc gplot data = mod2;
plot r2*age = female /vaxis=axis2 haxis=axis1 vref=0;
run;
quit;
proc univariate data = mod2 noprint; probplot r2 / normal(mu = est sigma=est color=blue l=1 w=1); run;