SAS Textbook Examples
Missing Data by
Paul D. Allison
Chapter 4: Maximum Likelihood
Table 4.1 on page 21 showing the number of nonmissing cases for each variable, and the means and standard deviations for those cases with data present.
data college; set 'd:datamiusnews'; run; proc means data=college n mean std ; var gradrat csat lenroll private stufac rmbrd act; run;
The MEANS Procedure
Variable N Mean Std Dev ------------------------------------------------ gradrat 1204 60.4053156 18.8890580 csat 779 967.9781772 123.5774927 lenroll 1297 6.1675196 0.9971460 private 1302 0.6390169 0.4804702 stufac 1300 14.8587692 5.1863985 rmbrd 783 4.1451149 1.1695883 act 714 22.1204482 2.5798990 ------------------------------------------------
Table 4.2 on page 22 using listwise deletion.
proc reg data = college; model gradrat = csat lenroll private stufac rmbrd; run; quit; The REG Procedure Model: MODEL1 Dependent Variable: gradrat
Analysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 5 75529 15106 78.68 <.0001 Error 449 86199 191.97929 Corrected Total 454 161728
Root MSE 13.85566 R-Square 0.4670 Dependent Mean 63.38462 Adj R-Sq 0.4611 Coeff Var 21.85966
Parameter Estimates
Parameter Standard Variable DF Estimate Error t Value Pr > |t|
Intercept 1 -35.02840 7.68461 -4.56 <.0001 csat 1 0.06727 0.00643 10.47 <.0001 lenroll 1 2.41705 0.95904 2.52 0.0121 private 1 13.58806 1.94612 6.98 <.0001 stufac 1 -0.12306 0.13188 -0.93 0.3513 rmbrd 1 2.16169 0.71364 3.03 0.0026
Table 4.3 on page 22 using EM algorithm. The output from proc mi is shown using proc print and proc iml is used to create the mean and standard deviation for each variable.
proc mi data = college seed = 37851 nimpute = 0 noprint; em itprint outem = outem ; var gradrat csat lenroll private stufac rmbrd act; run; proc print data = outem; run;
Obs _TYPE_ _NAME_ gradrat csat lenroll private stufac rmbrd act
1 MEAN 59.86 957.88 6.1694 0.63902 14.864 4.0726 22.220
2 COV gradrat 355.71 1352.99 -0.4998 3.60825 -31.142 10.3847 30.584
3 COV csat 1352.99 14745.15 23.2381 9.38160 -198.406 67.1206 298.906
4 COV lenroll -0.50 23.24 0.9937 -0.29640 1.382 -0.0188 0.470
5 COV private 3.61 9.38 -0.2964 0.23067 -0.916 0.1885 0.291
6 COV stufac -31.14 -198.41 1.3822 -0.91560 26.886 -1.6854 -4.122
7 COV rmbrd 10.38 67.12 -0.0188 0.18853 -1.685 1.3290 1.514
8 COV act 30.58 298.91 0.4695 0.29118 -4.122 1.5143 7.353
proc iml;
use outem;
read all var _num_ into A;
read all var {_name_} where (_type_ ^="MEAN") into variable ;
r=nrow(A);
v=ncol(A);
mvec = t(A[1,]);
var = sqrt(vecdiag(A[2:r,]));
print variable " " mvec[colname="Mean" label=" " format=F6.2] " "
var[colname="Std. Dev" label=" " format=F6.3];
quit;
VARIABLE Mean Std. Dev
gradrat 59.86 18.860
csat 957.88 121.43
lenroll 6.17 0.997
private 0.64 0.480
stufac 14.86 5.185
rmbrd 4.07 1.153
act 22.22 2.712
Table 4.4 for the correlations.
proc iml; use outem ; read all var _num_ where (_type_ ^="MEAN") into A; b = sqrt(vecdiag(A)); corrb = diag(1/b)*A*diag(1/b); print "Correlation From the EM Algorithm"; print corrb[label=" "]; quit;
Correlation From the EM Algorithm
1 0.5907701 -0.026587 0.3983338 -0.318444 0.4776146 0.5980197
0.5907701 1 0.1919785 0.1608618 -0.315116 0.4794722 0.907774
-0.026587 0.1919785 1 -0.6191 0.2674224 -0.016402 0.1737042
0.3983338 0.1608618 -0.6191 1 -0.367662 0.3405044 0.2235772
-0.318444 -0.315116 0.2674224 -0.367662 1 -0.281956 -0.29315
0.4776146 0.4794722 -0.016402 0.3405044 -0.281956 1 0.4843963
0.5980197 0.907774 0.1737042 0.2235772 -0.29315 0.4843963 1
Table 4.5 based on EM algorithm result. We first create a covariance type of data adding the number of observations to the matrix from proc mi.
data outem1; set outem end=last; array temp(*) _numeric_; output; if last then do; _type_ = "N"; _name_ = " "; do i = 1 to dim(temp); temp(i) = 1302; end; output; end; drop i; run; proc reg data = outem1(type=cov) ; model gradrat = csat lenroll private stufac rmbrd; run; quit;
The REG Procedure
Model: MODEL1
Dependent Variable: gradrat
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 5 216812 43362 228.47 <.0001
Error 1296 245971 189.79261
Corrected Total 1301 462783
Root MSE 13.77652 R-Square 0.4685
Dependent Mean 59.86180 Adj R-Sq 0.4664
Coeff Var 23.01388
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 -32.39455 4.35463 -7.44 <.0001
csat 1 0.06688 0.00390 17.14 <.0001
lenroll 1 2.08321 0.53938 3.86 0.0001
private 1 12.91450 1.14657 11.26 <.0001
stufac 1 -0.18139 0.08412 -2.16 0.0312
rmbrd 1 2.40383 0.40010 6.01 <.0001
Table 4.6 on page 27, difficult to do in SAS.
Chapter 5: Multiple Imputation: Basics
Single Random Imputation
The program here is to illustrate the idea presented in this section. The results are not exactly the same because the randomness involved in generating the data sets. We first generate a data set of 10,000 cases, where variable x and y are drawn from a standard, bivariate normal distribution with a correlation .3.
data page28;
do subject=1 to 10000;
y=rannor(123456);
x=.3*y+sqrt(1-(.3)**2)*rannor(0);
output;
end;
run;
proc corr data = page28 noprob;
var x y;
run;
The CORR Procedure
2 Variables: x y
Simple Statistics
Variable N Mean Std Dev Sum Minimum Maximum
x 10000 0.00897 1.00804 89.68395 -4.12924 4.09470
y 10000 0.01985 0.99246 198.45285 -4.37004 4.14573
Pearson Correlation Coefficients, N = 10000
x y x 1.00000 0.30019 y 0.30019 1.00000
At this point, we are going to create a data set with half of the x values assigned to be missing completely at random. The new variable is called mx in the new data set.
data page28_miss; set page28 nobs=n; retain index 10000 count 5000; percent = count /index; if uniform(_n_) < percent then do; a = 1; mx = .; count = count - 1; end; else do; a = 0; mx = x; end; index = index - 1; run; proc corr data = page28_miss noprob; var mx y; run;
The CORR Procedure
2 Variables: mx y
Simple Statistics
Variable N Mean Std Dev Sum Minimum Maximum
mx 5000 0.00400 1.00469 19.97631 -3.59469 4.09470
y 10000 0.01985 0.99246 198.45285 -4.37004 4.14573
Pearson Correlation Coefficients
Number of Observations
mx y
mx 1.00000 0.29610
5000 5000
y 0.29610 1.00000
5000 10000
Now we use the predicted values from the regression of mx on y to substitute for the missing values and check on the correlation based on the substitution. The correlation is .397, overestimating.
proc reg data = page28_miss; model mx = y; run; quit; data page28_impute; set page28_miss; if mx = . then imx = -.00194 + .29571*y; else imx = x; run;
proc corr data = page28_impute noprob;
var imx y;
run;
Parameter Estimates
Parameter Standard
Variable DF Estimate Error t Value Pr > |t|
Intercept 1 -0.00194 0.01358 -0.14 0.8862
y 1 0.29571 0.01349 21.92 <.0001
The CORR Procedure
2 Variables: imx y
Simple Statistics
Variable N Mean Std Dev Sum Minimum Maximum
imx 10000 0.00393 0.73928 39.27347 -3.59469 4.09470
y 10000 0.01985 0.99246 198.45285 -4.37004 4.14573
Pearson Correlation Coefficients, N = 10000
imx y
imx 1.00000 0.39698
y 0.39698 1.00000
Finally, we correct the bias by taking random draws from the residual distribution of mx and adding them back to the predicted values of mx.
data page28_impute_random; set page28_miss; if mx = . then imx = -.00194 + .29571*y + .95073*rannor(_n_); else imx = x; run; proc corr data = page28_impute_random noprob; var imx y; run;
The CORR Procedure
2 Variables: imx y
Simple Statistics
Variable N Mean Std Dev Sum Minimum Maximum
imx 10000 -0.00443 1.00081 -44.33937 -3.67296 4.09470
y 10000 0.01985 0.99246 198.45285 -4.37004 4.14573
Pearson Correlation Coefficients, N = 10000
imx y
imx 1.00000 0.29643
y 0.29643 1.00000
Multiple Random Imputation
Table 5.1 on page 30 and the calculation of standard error for the mean of the correlation estimates.
Since we have to run a loop here for at least 8 times as shown in the text, we make use of some SAS macro programming here. The macro loop is based on the data set created earlier in the previous section and takes one parameter of number of times that we want to estimate the correlation coefficient.
%macro loop(num);
%do i = 1 %to #
data page28_impute_random;
set page28_miss;
if mx = . then
imx = -.00194 + .29571*y + .95073*rannor(_n_+&i*10000);
else imx = x;
run;
proc corr data = page28_impute_random noprob OUTP=pcorr&i ;
var imx y;
run;
%end;
data pcorr;
set %do i = 1 %to #
pcorr&i
%end;
;
if _name_="imx";
se = (1 - y*y)/sqrt(10000);
keep y se;
label y = "correlation";
label se = "S.E.";
run;
proc print data=pcorr label noobs;
format se 7.5;
run;
proc sql;
select ymean as mean_of_r, semean as mean_of_se,
sqrt((1/&num)*set + (1+1/&num)*(1/(&num-1))*(y2sum -&num*ymean**2)) as se_r_avg,
sqrt((1/&num)*set + (1+1/&num)*(1/(&num-1))*(y2sum -&num*ymean**2))/semean*100-100 as ratio
from (select sum(se**2) as set, sum(y*y) as y2sum, mean(y) as ymean, mean(se) as semean
from pcorr);
quit;
%mend;
%loop(8)
correlation S.E.
0.29445 0.00913 0.28309 0.00920 0.28426 0.00919 0.28972 0.00916 0.29658 0.00912 0.29449 0.00913 0.30680 0.00906 0.30502 0.00907
mean_of_r mean_of_se se_r_avg ratio ----------------------------------------- 0.294303 0.009133 0.012945 41.74063
Allowing for Random Variation in the Parameter Estimates
Table 5.2 on page 32.
proc mi data=page28_miss seed=37851 nimpute = 8 out=outmi;; mcmc nbiter = 500 niter = 200; var mx y; run; proc corr data = outmi noprob; by _imputation_; var mx y; ods output PearsonCorr=test; run;
data pcorr; set test; if variable ="mx"; se = (1 - y*y)/sqrt(10000); keep y se; label y = "correlation"; label se = "S.E."; run;
proc print data=pcorr label noobs;
format se 7.5;
run;
%let num = 8;
proc sql;
select ymean as mean_of_r, semean as mean_of_se,
sqrt((1/&num)*set + (1+1/&num)*(1/(&num-1))*(y2sum -&num*ymean**2)) as se_r_avg,
sqrt((1/&num)*set + (1+1/&num)*(1/(&num-1))*(y2sum -&num*ymean**2))/semean*100-100 as ratio
from (select sum(se**2) as set, sum(y*y) as y2sum, mean(y) as ymean, mean(se) as semean
from pcorr);
quit;
correlation S.E.
0.27640 0.00924 0.28710 0.00918 0.29265 0.00914 0.30048 0.00910 0.29319 0.00914 0.30283 0.00908 0.28291 0.00920 0.30148 0.00909
mean_of_r mean_of_se se_r_avg ratio ----------------------------------------- 0.292131 0.009146 0.013601 48.71186
MI Example 1 on page 41
Note: The SAS code in the book is for SAS 8.1. Since the publishing of Missing Data, SAS has modified the imputation procedures. The results on this webpage will not match with the results in the book precisely, even though the code is the same.
Figure 5.1 on page 44.
proc mi data = mycollege out = college nimpute=1 seed = 1401
minimum = 0 600 . . 0 1.26 11
maximum = 100 1400 . . 100 8.70 31
round = 1 1 1 1 . 1 1 1;
var gradrat csat lenroll private stufac rmbrd act;
mcmc nbiter = 100 niter=1 outiter (cov) =g100;
run;
quit;
data fig5_1;
set g100 (where =(_name_="csat") keep = _iteration_ _name_ gradrat csat);
slope = gradrat/csat;
iteration = 100 + _iteration_;
run;
symbol i = spline;
proc gplot data = fig5_1;
plot slope*iteration ;
run;
quit;
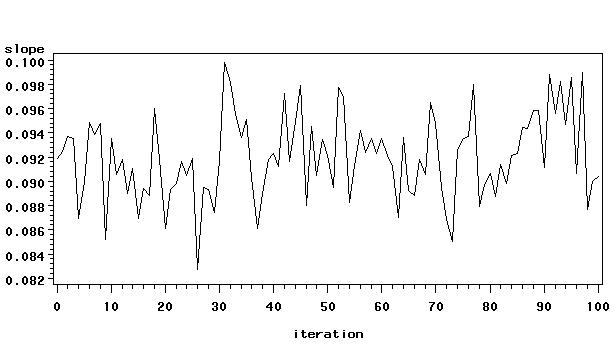
Table 5.3 on page 45.
proc mi data = mycollege out = college seed = 1401
minimum = 0 600 . . 0 1.26 11
maximum = 100 1400 . . 100 8.70 31
round = 1 1 1 1 . 1 1 1;
var gradrat csat lenroll private stufac rmbrd act;
mcmc nbiter = 500 niter = 200 chain = multiple ;
run;
proc reg data = college outest=estimate outseb; model gradrat = csat lenroll private stufac rmbrd; by _imputation_; run; proc transpose data = estimate out=wide (drop=_label_) ; by _imputation_; var intercept csat lenroll private stufac rmbrd; run; proc sort data = wide; by _name_; run; proc print data = wide (rename=(col1=est col2=stderr)); run;
Obs _Imputation_ _NAME_ est stderr
1 1 Intercept -32.7293 4.35540 2 2 Intercept -33.6320 4.33494 3 3 Intercept -31.0291 4.36411 4 4 Intercept -29.5485 4.38421 5 5 Intercept -30.7938 4.29643 6 1 csat 0.0645 0.00390 7 2 csat 0.0692 0.00387 8 3 csat 0.0670 0.00398 9 4 csat 0.0654 0.00400 10 5 csat 0.0646 0.00388 11 1 lenroll 2.3325 0.53602 12 2 lenroll 2.0885 0.53881 13 3 lenroll 2.0575 0.54997 14 4 lenroll 1.9638 0.54982 15 5 lenroll 2.0654 0.54046 16 1 private 13.6415 1.12855 17 2 private 12.9080 1.13730 18 3 private 13.2238 1.14985 19 4 private 12.8049 1.16374 20 5 private 12.7397 1.14009 21 1 rmbrd 2.5091 0.39269 22 2 rmbrd 2.0074 0.39868 23 3 rmbrd 2.0282 0.41058 24 4 rmbrd 2.1758 0.40537 25 5 rmbrd 2.6136 0.39714 26 1 stufac -0.1677 0.08419 27 2 stufac -0.1445 0.08445 28 3 stufac -0.1927 0.08535 29 4 stufac -0.1667 0.08487 30 5 stufac -0.1805 0.08368
Figure 5.2 on page 46.
We have created a data set called fig5_1 for figure 5.1 previously and we will continue to use it here.
ods output corrgraph=fig5_2 (keep = lag correlation); proc arima data=fig5_1; identify var= slope nlag=100; run; quit;
symbol i=needle w=5; axis1 order=(1 to 100 by 1) ; axis2 order = (-.2 to .3 by .05) label=(a=90); proc gplot data = fig5_2; where lag~=0; format correlation 5.2; plot correlation*lag /haxis=axis1 vaxis=axis2; run; quit;
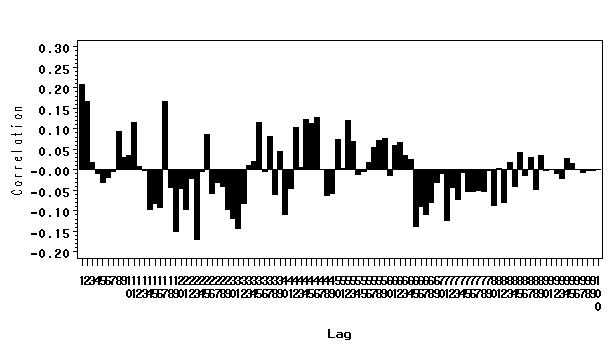
Figure 5.3 on page 48.
proc mi data = mycollege out = college seed = 1401
minimum = 0 600 . . 0 1.26 11
maximum = 100 1400 . . 100 8.70 31
round = 1 1 1 1 . 1 1 1;
var gradrat csat lenroll private stufac rmbrd act;
mcmc nbiter = 500 niter = 200 ;
run;
proc reg data = college outest=estimate covout; model gradrat = csat lenroll private stufac rmbrd; by _imputation_; run;
proc mianalyze data = estimate; modeleffects intercept csat lenroll private stufac rmbrd; run;
Multiple Imputation Variance Information
Relative Fraction
-----------------Variance----------------- Increase Missing
Parameter Between Within Total DF in Variance Information
intercept 5.112237 19.334782 25.469467 68.947 0.317287 0.261967 csat 0.000008409 0.000015729 0.000025820 26.191 0.641501 0.432540 lenroll 0.042972 0.293037 0.344604 178.63 0.175973 0.159004 private 0.086331 1.313014 1.416612 747.93 0.078900 0.075599 stufac 0.002583 0.007161 0.010260 43.837 0.432809 0.331872 rmbrd 0.093636 0.158752 0.271115 23.287 0.707789 0.458998
Multiple Imputation Parameter Estimates
Parameter Estimate Std Error 95% Confidence Limits DF
intercept -34.159501 5.046728 -44.2276 -24.0914 68.947 csat 0.068021 0.005081 0.0576 0.0785 26.191 lenroll 2.176581 0.587030 1.0182 3.3350 178.63 private 13.519104 1.190215 11.1825 15.8557 747.93 stufac -0.132473 0.101291 -0.3366 0.0717 43.837 rmbrd 2.181653 0.520687 1.1053 3.2580 23.287
Multiple Imputation Parameter Estimates
t for H0: Parameter Minimum Maximum Theta0 Parameter=Theta0 Pr > |t|
intercept -37.231787 -32.226869 0 -6.77 <.0001 csat 0.064459 0.071636 0 13.39 <.0001 lenroll 1.891638 2.410736 0 3.71 0.0003 private 13.014425 13.719135 0 11.36 <.0001 stufac -0.178505 -0.049020 0 -1.31 0.1977 rmbrd 1.842707 2.509079 0 4.19 0.0003
Figure 5.4 on page 49. We choose seed to be 12345 for this example.
proc mi data = mycollege out = college seed = 12345
minimum = 0 600 . . 0 1.26 11
maximum = 100 1400 . . 100 8.70 31
round = 1 1 1 1 . 1 1 1;
var gradrat csat lenroll private stufac rmbrd act;
mcmc nbiter = 500 niter = 200 ;
run;
proc reg data = college outest=estimate covout; model gradrat = csat lenroll private stufac rmbrd; by _imputation_; run;
proc mianalyze data = estimate; modeleffects intercept csat lenroll private stufac rmbrd; run;
Multiple Imputation Variance Information
Relative Fraction
-----------------Variance----------------- Increase Missing
Parameter Between Within Total DF in Variance Information
intercept 3.045733 19.316622 22.971502 158.01 0.189209 0.169550 csat 0.000004876 0.000015251 0.000021102 52.026 0.383665 0.303550 lenroll 0.128509 0.291455 0.445666 33.408 0.529109 0.381950 private 0.318826 1.315225 1.697816 78.772 0.290895 0.244290 stufac 0.005102 0.007133 0.013255 18.751 0.858295 0.511354 rmbrd 0.211943 0.159753 0.414084 10.603 1.592022 0.670922
Multiple Imputation Parameter Estimates
Parameter Estimate Std Error 95% Confidence Limits DF
intercept -32.615425 4.792859 -42.0818 -23.1491 158.01 csat 0.068855 0.004594 0.0596 0.0781 52.026 lenroll 2.053894 0.667582 0.6963 3.4115 33.408 private 13.054872 1.303003 10.4612 15.6486 78.772 stufac -0.194243 0.115129 -0.4354 0.0469 18.751 rmbrd 2.036734 0.643494 0.6139 3.4595 10.603
Multiple Imputation Parameter Estimates
t for H0: Parameter Minimum Maximum Theta0 Parameter=Theta0 Pr > |t|
intercept -34.976524 -30.583509 0 -6.81 <.0001 csat 0.066110 0.072156 0 14.99 <.0001 lenroll 1.664030 2.472921 0 3.08 0.0042 private 12.541527 13.984207 0 10.02 <.0001 stufac -0.311137 -0.122689 0 -1.69 0.1081 rmbrd 1.469074 2.718011 0 3.17 0.0094
Chapter 6: Multiple Imputation: Complications
Table 6.1 on page 51.
Method 1: Interaction term is created based on the imputed data.
proc mi data = mycollege out = college seed = 1401
minimum = 0 600 . . 0 1.26 11
maximum = 100 1400 . . 100 8.70 31
round = 1 1 1 1 . 1 1 1;
var gradrat csat lenroll private stufac rmbrd act;
mcmc nbiter = 500 niter = 200 ;
run;
data method1; set college; csatXpri = csat*private; run; proc reg data = method1 outest=estimate covout; model gradrat = csat lenroll private stufac rmbrd csatXpri; by _imputation_; run;
proc mianalyze data = estimate; modeleffects intercept csat lenroll private stufac rmbrd csatXpri; run;
Parameter Estimate Std Error
intercept -39.490344 6.718937 csat 0.073566 0.006494 lenroll 2.195024 0.589931 private 21.183207 7.870483 stufac -0.136234 0.101501 rmbrd 2.210600 0.529051 csatXpri -0.008134 0.008130
Parameter Pr > |t|
intercept <.0001 csat <.0001 lenroll 0.0003 private 0.0090 stufac 0.1865 rmbrd 0.0004 csatXpri 0.3202
Method 2: Separate chains of data augmentation for private colleges and for public colleges.
data private public;
set mycollege ;
if private = 1 then output private;
else output public;
run;
proc mi data = private out = private_imp seed = 1401
minimum = 0 600 . 0 1.26 11
maximum = 100 1400 . 100 8.70 31
round = 1 1 1 1 1 1 1;
var gradrat csat lenroll stufac rmbrd act;
mcmc nbiter = 500 niter = 200 ;
run;
proc mi data = public out = public_imp seed = 1401
minimum = 0 600 . 0 1.26 11
maximum = 100 1400 . 100 8.70 31
round = 1 1 1 1 1 1 1;
var gradrat csat lenroll stufac rmbrd act;
mcmc nbiter = 500 niter = 200 ;
run;
data method2;
set private_imp public_imp;
csatXpri = csat*private;
run;
proc sort data = method2;
by _imputation_;
run;
proc reg data = method2 outest=estimate2 covout;
model gradrat = csat lenroll private stufac rmbrd csatXpri;
by _imputation_;
run;
proc mianalyze data = estimate2;
modeleffects intercept csat lenroll private stufac rmbrd csatXpri;
run;
Parameter Estimate
intercept -49.672789 csat 0.084559 lenroll 2.230984 private 35.992044 stufac -0.209713 rmbrd 2.384819 csatXpri -0.023945
Parameter Pr > |t|
intercept <.0001 csat <.0001 lenroll 0.0004 private 0.0001 stufac 0.1062 rmbrd 0.0412 csatXpri 0.0076
Method 3: Creating interaction term before imputation.
data method3; set mycollege; csatXpri = csat*private; run;
proc mi data = method3 out = m3_out seed = 1401
minimum = 0 600 . . 0 1.26 11 .
maximum = 100 1400 . . 100 8.70 31 1400
round = 1 1 1 1 . 1 1 1 1;
var gradrat csat lenroll private stufac rmbrd act csatXpri;
mcmc nbiter = 500 niter = 200 ;
run;
proc reg data = m3_out outest=estimate3 covout;
model gradrat = csat lenroll private stufac rmbrd csatXpri;
by _imputation_;
run;
proc mianalyze data = estimate3;
modeleffects intercept csat lenroll private stufac rmbrd csatXpri;
run;
Parameter Estimate
intercept -54.317589 csat 0.088825 lenroll 2.147010 private 41.531167 stufac -0.165995 rmbrd 2.479377 csatXpri -0.029622
Parameter Pr > |t|
intercept <.0001 csat <.0001 lenroll 0.0002 private <.0001 stufac 0.0752 rmbrd 0.0003 csatXpri 0.0028
Example on page 61. The data set is created based on a text file. You can download the text file here.
data college;
infile "https://stats.idre.ucla.edu/wp-content/uploads/2016/02/usnews3.txt" missover ;
input #2 prit 1-2 csat 11-15 act 16-18 nfresh 53-57
#3 tuition_in 13-18 tuition_out 19-24
#3 rm 30-34 board 35-39 stufac 63-67 gradrat 77-80;
rmbrd = (rm + board)/1000;
private = prit - 1;
lenroll = log(nfresh);
run;
data page61; set college; if tuition_in ~=. ; run;
The listwise deletion method result for the mean and standard deviation is obtained by using proc means.
proc means data = page61 mean stderr min max ; var board ; run;
The MEANS Procedure
Variable Mean Std Error Minimum Maximum -------------------------------------------------------------------------- board 2060.28 23.3527380 531.0000000 6250.00 --------------------------------------------------------------------------
The EM estimate of correlation between variable board and tuition_in obtained using proc mi. Based on the covariance matrix from proc mi, we calculated the correlation using a little bit of proc iml.
proc mi data = page61 seed = 37851 nimpute = 0 ; em itprint outem = outem ; var board tuition_in; run;
The MI Procedure
EM (MLE) Parameter Estimates
_TYPE_ _NAME_ board tuition_in
MEAN 2031.715414 7897.274371
COV board 424466 1933499
COV tuition_in 1933499 28580357
EM (Posterior Mode) Estimates _TYPE_ _NAME_ board tuition_in MEAN 2031.694808 7897.274371 COV board 423074 1929028 COV tuition_in 1929028 28513109
proc iml; use outem ; read all var _num_ where (_type_ ^="MEAN") into A; b = sqrt(vecdiag(A)); corrb = diag(1/b)*A*diag(1/b); print "Correlation From the EM Algorithm"; print corrb[label=" "]; quit;
Correlation From the EM Algorithm
1 0.5551223 0.5551223 1
The multiple imputation using data augmentation is obtained below using proc mi. The result is not exactly the same from the book. It may be because of the different choice of seed.
proc mi data = page61 out = impage61 seed = 12345; var board tuition_in; mcmc nbiter = 500 niter = 200 outiter (cov) = outiter ; run;
The MI Procedure
Multiple Imputation Parameter Estimates
Variable Mean Std Error 95% Confidence Limits DF
board 2036.013053 21.328071 1993.225 2078.802 52.486
Multiple Imputation Parameter Estimates
t for H0: Variable Minimum Maximum Mu0 Mean=Mu0 Pr > |t|
board 2025.248823 2049.634738 0 95.46 <.0001
To see how the data augmentation has done, we can use proc univariate to see the extreme values imputed. There is a negative imputed value and the five lowest values are way below the observed minimum for variable board.
proc univariate data = impage61 ; var board ; run;
The UNIVARIATE Procedure Variable: board
Extreme Observations
------Lowest------ ----Highest---
Value Obs Value Obs
-23.8777 3850 6250 937 34.4726 583 6250 2209 34.5104 4320 6250 3481 72.0237 5418 6250 4753 223.5688 2429 6250 6025
Now the regression result is as follows and will be used to do the sampling.
proc reg data = page61; model board = tuition_in; run; quit;
The REG Procedure Dependent Variable: board
Analysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F Model 1 111364505 111364505 378.29 <.0001 Error 794 233744119 294388 Corrected Total 795 345108624
Root MSE 542.57540 R-Square 0.3227 Dependent Mean 2060.27764 Adj R-Sq 0.3218 Coeff Var 26.33506
Parameter Estimates
Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 1497.41087 34.74671 43.10 <.0001 tuition_in 1 0.06765 0.00348 19.45 <.0001
MI Example 3 using hip data set. Notice that hip data set here has four waves rather than three. The last three waves are after releasing from the hospital. The output for parameter estimates on each individual SID has been omitted in the output part.
Table 6.4 on page 76.
Part 1: Listwise deletion by person
data hip2; set hip (where = (wave~=1)); wdum2 = (wave=2); wdum3 = (wave=3); run; proc sql; create table tokeep as select sid, count(cesd)+ count(srh) + count(walk) + count(adl) + count(pain) as check from hip2 group by sid; quit; proc sql; create table hip_list as select hip2.* from hip2, tokeep where tokeep.check = 15 and tokeep.sid = hip2.sid; quit;
proc glm data = hip_list; class sid; model cesd = srh walk adl pain wdum2 wdum3 sid/solution; run; quit;
Dependent Variable: CESD
Sum of Source DF Squares Mean Square F Value Pr > F
Model 106 12565.89863 118.54621 7.94 <.0001
Error 196 2926.95063 14.93342
Corrected Total 302 15492.84925
R-Square Coeff Var Root MSE CESD Mean
0.811077 41.46229 3.864379 9.320224
Standard Parameter Estimate Error t Value Pr > |t|
Intercept 9.35357013 B 2.76111252 3.39 0.0009 SRH 2.34162590 0.58561467 4.00 <.0001 WALK -1.55214163 0.77085849 -2.01 0.0454 ADL -0.67651277 0.52774928 -1.28 0.2014 PAIN 0.03117661 0.17860643 0.17 0.8616 wdum2 8.00426420 0.64960304 12.32 <.0001 wdum3 7.04479504 0.57893929 12.17 <.0001
Part 2: Listwise deletion by person-time
proc glm data = hip2; class sid; model cesd = srh walk adl pain wdum2 wdum3 sid/solution; run; quit;
Dependent Variable: CESD
Sum of Source DF Squares Mean Square F Value Pr > F
Model 200 23301.31535 116.50658 6.43 <.0001
Error 252 4565.64090 18.11762
Corrected Total 452 27866.95625
R-Square Coeff Var Root MSE CESD Mean
0.836163 44.23388 4.256480 9.622669
Parameter Estimate Error t Value Pr > |t|
Intercept 9.37277265 B 2.95992726 3.17 0.0017 SRH 1.64132997 0.55572595 2.95 0.0034 WALK -1.38062437 0.76131946 -1.81 0.0710 ADL -0.33546552 0.53881181 -0.62 0.5341 PAIN 0.21506213 0.16756607 1.28 0.2005 wdum2 8.78676092 0.61275103 14.34 <.0001 wdum3 7.93044189 0.51985970 15.25 <.0001
Part 3: Data augmentation by person-time. Notice that the result here is quite different from the result in the book. This may be due to several reasons. First of all, the result in the book was done in an earlier version of SAS. Secondly, there is a natural randomness, e.g., the choice of seed. The result below is much closer to the second method above.
proc mi data = hip2 out = hip2_out1 seed = 1401; var cesd srh walk adl pain wdum2 wdum3; mcmc nbiter = 500 niter = 200 ; run;
ods output ParameterEstimates = est3; proc glm data = hip2_out1 outstat= test ; by _imputation_; class sid; model cesd = srh walk adl pain wdum2 wdum3 sid /solution; run; quit; proc mianalyze parms = est3; modeleffects intercept srh walk adl pain wdum2 wdum3; run;
Multiple Imputation Parameter Estimates
Parameter Estimate Std Error 95% Confidence Limits DF
intercept 7.112057 3.260271 0.71830 13.50582 2065.1 srh 2.331491 0.422612 1.50305 3.15993 7312.9 walk -1.364671 0.780848 -2.92266 0.19332 68.41 adl -0.287099 0.372109 -1.05010 0.47590 27.386 pain 0.456069 0.199120 0.03956 0.87258 19.174 wdum2 8.805726 0.691685 7.37941 10.23204 24.406 wdum3 7.692605 0.725346 6.13175 9.25347 13.525
Part 4: Data augmentation by person.
%macro towide(var); proc transpose data = hip2 out=hip_&var prefix=&var; by sid; id wave; var &var ; run; %mend; %towide(cesd); %towide(srh); %towide(walk); %towide(adl); %towide(pain); data hip_wide; merge hip_cesd hip_srh hip_walk hip_adl hip_pain; by sid; run;
proc mi data = hip_wide out = hip3 seed = 1401; var cesd: srh: walk: adl: pain:; mcmc nbiter = 500 niter = 200 ; run; data hip4; set hip3; array c(3) cesd:; array s(3) srh:; array w(3) walk:; array a(3) adl:; array p(3) pain:; do wave = 1 to 3; cesd = c(wave); srh = s(wave); walk = w(wave); adl = a(wave); pain = p(wave); output; end; keep sid cesd srh walk adl pain wave _imputation_; run; data hip4a; set hip4; wdum2 = (wave=1); wdum3 = (wave=2); run; ods output parameterestimates = est4; proc glm data = hip4a ; by _imputation_; class sid; model cesd = srh walk adl pain wdum2 wdum3 sid /solution; run; quit; proc mianalyze parms = est4; modeleffects intercept srh walk adl pain wdum2 wdum3; run;
Multiple Imputation Parameter Estimates
Parameter Estimate Std Error 95% Confidence Limits DF
intercept 9.250156 3.604442 1.95764 16.54267 38.694 srh 1.480490 0.659000 0.04960 2.91138 12.386 walk -0.889094 0.770854 -2.43282 0.65463 56.799 adl -0.113741 0.665701 -1.72931 1.50183 6.2114 pain 0.214135 0.216721 -0.26201 0.69028 11.163 wdum2 8.943499 0.616950 7.68654 10.20046 31.824 wdum3 8.166227 0.568707 7.00730 9.32515 31.648
