You can download the dataset for this chapter by clicking here: https://stats.idre.ucla.edu/wp-content/uploads/2016/02/sfa.sas7bdat.
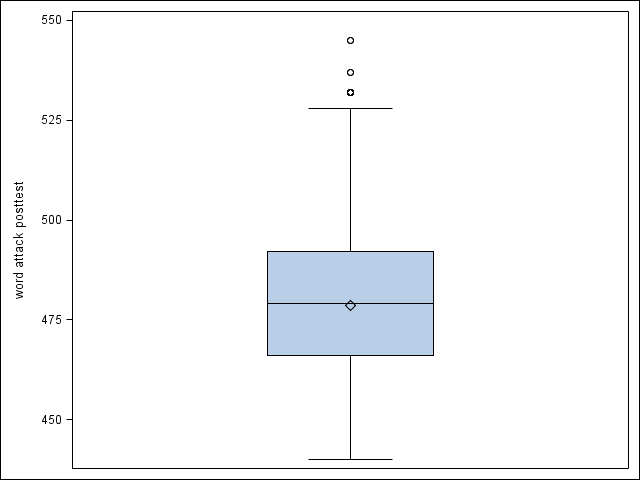
Descriptive statistics for the variable wattack. Notice the floor effect which cannot be resolved by a straightforward transformation. (Note these analyses are not shown in the text.)
proc univariate data= sfa;
var wattack;
run;
The UNIVARIATE Procedure
Variable: wattack (word attack posttest)
Moments
N 2334 Sum Weights 2334
Mean 478.51928 Sum Observations 1116864
Std Deviation 19.8787218 Variance 395.16358
Skewness -0.1655814 Kurtosis -0.1967402
Uncorrected SS 535362874 Corrected SS 921916.632
Coeff Variation 4.15421543 Std Error Mean 0.41146986
Basic Statistical Measures
Location Variability
Mean 478.5193 Std Deviation 19.87872
Median 479.0000 Variance 395.16358
Mode 440.0000 Range 105.00000
Interquartile Range 26.00000
Tests for Location: Mu0=0
Test -Statistic- -----p Value------
Student's t t 1162.951 Pr > |t| <.0001
Sign M 1167 Pr >= |M| <.0001
Signed Rank S 1362473 Pr >= |S| <.0001
Quantiles (Definition 5)
Quantile Estimate
100% Max 545
99% 525
95% 509
90% 503
75% Q3 492
50% Median 479
25% Q1 466
10% 449
5% 440
1% 440
0% Min 440
The UNIVARIATE Procedure
Variable: wattack (word attack posttest)
Extreme Observations
----Lowest---- ----Highest---
Value Obs Value Obs
440 2327 532 1994
440 2323 537 1008
440 2322 537 1442
440 2320 545 1640
440 2312 545 1847
proc sgplot data=sfa;
vbox wattack;
run;
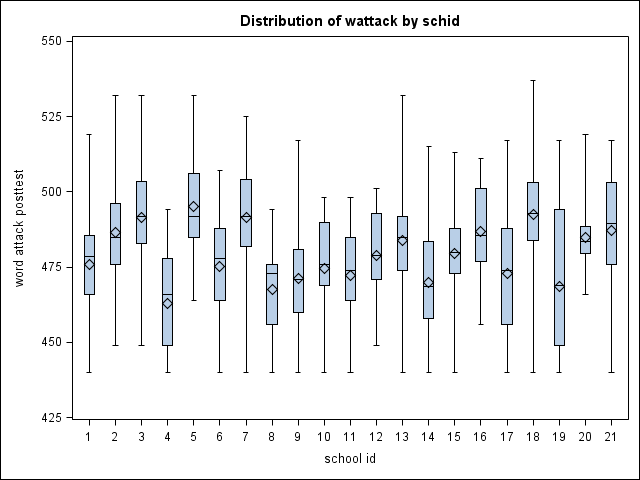
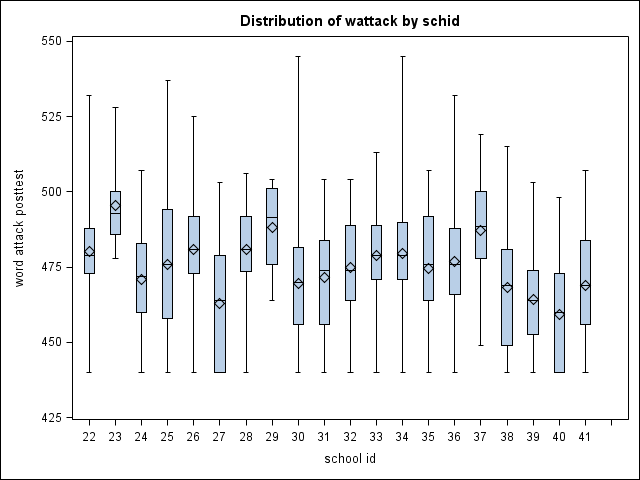
Descriptive analyses of wattack by school (schid). Note the floor effect is present in most schools. (Not shown in text.)
proc means data=sfa;
class schid;
vars wattack;
run;
The MEANS Procedure
Analysis Variable : wattack word attack posttest
N
school id Obs N Mean Std Dev Minimum Maximum
1 52 52 475.7307692 16.1598818 440.0000000 519.0000000
2 116 116 486.6034483 15.3106268 449.0000000 532.0000000
3 68 68 491.3676471 16.8469001 449.0000000 532.0000000
4 34 34 462.9117647 16.5517877 440.0000000 494.0000000
5 47 47 495.0851064 14.9678348 464.0000000 532.0000000
6 87 87 475.1149425 18.0776267 440.0000000 507.0000000
7 83 83 491.5301205 16.1911880 440.0000000 525.0000000
8 22 22 467.5000000 13.9412031 440.0000000 494.0000000
9 95 95 471.1052632 17.6962995 440.0000000 517.0000000
10 27 27 474.5555556 19.0774400 440.0000000 498.0000000
11 43 43 472.1860465 16.6879709 440.0000000 498.0000000
12 27 27 478.9629630 13.2185228 449.0000000 501.0000000
13 62 62 483.8709677 14.5641418 440.0000000 532.0000000
14 36 36 469.8888889 17.1876663 440.0000000 515.0000000
15 54 54 479.5555556 15.9712793 440.0000000 513.0000000
16 36 36 486.7500000 14.8696719 456.0000000 511.0000000
17 41 41 472.9512195 22.7199815 440.0000000 517.0000000
18 109 109 492.5963303 17.5209500 440.0000000 537.0000000
19 23 23 468.7391304 23.8560406 440.0000000 517.0000000
20 20 20 484.7500000 11.1349379 466.0000000 519.0000000
21 134 134 487.2313433 19.0700782 440.0000000 517.0000000
22 106 106 480.2735849 18.0182622 440.0000000 532.0000000
23 36 36 495.3333333 12.1161050 478.0000000 528.0000000
The MEANS Procedure
Analysis Variable : wattack word attack posttest
N
school id Obs N Mean Std Dev Minimum Maximum
24 48 48 470.7708333 17.1504477 440.0000000 507.0000000
25 52 52 476.0192308 23.5134425 440.0000000 537.0000000
26 66 66 480.9696970 18.0264504 440.0000000 525.0000000
27 41 41 462.9512195 19.4601532 440.0000000 503.0000000
28 56 56 480.8392857 15.7823570 440.0000000 506.0000000
29 10 10 488.1000000 15.1983186 464.0000000 504.0000000
30 24 24 469.6250000 22.4185725 440.0000000 545.0000000
31 61 61 471.5245902 17.9662708 440.0000000 504.0000000
32 58 58 474.7241379 17.7722365 440.0000000 504.0000000
33 41 41 478.8780488 19.1992124 440.0000000 513.0000000
34 79 79 479.4177215 19.1850687 440.0000000 545.0000000
35 57 57 474.4210526 18.7349438 440.0000000 507.0000000
36 85 85 476.9294118 20.6321457 440.0000000 532.0000000
37 58 58 487.1896552 16.9275618 449.0000000 519.0000000
38 37 37 468.1891892 21.3174913 440.0000000 515.0000000
39 36 36 464.3611111 16.3255326 440.0000000 503.0000000
40 107 107 459.2523364 16.9739498 440.0000000 498.0000000
41 60 60 468.9333333 17.3536170 440.0000000 507.0000000
proc boxplot data=sfa;
plot wattack*schid;
run;
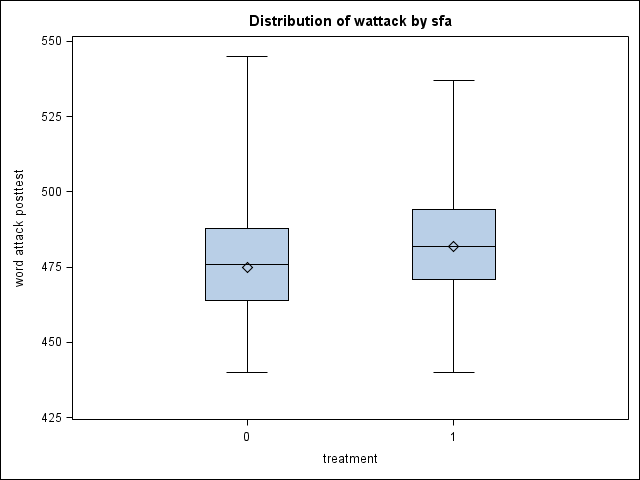
Descriptive analyses of wattack by experimental condition (sfa). (Not shown in text.)
proc univariate data= sfa;
class sfa;
var wattack;
run;
The UNIVARIATE Procedure
Variable: wattack (word attack posttest)
sfa = 0
Moments
N 1118 Sum Weights 1118
Mean 474.824687 Sum Observations 530854
Std Deviation 20.0523853 Variance 402.098155
Skewness -0.020796 Kurtosis -0.1872213
Uncorrected SS 252511728 Corrected SS 449143.639
Coeff Variation 4.22311346 Std Error Mean 0.59971531
Basic Statistical Measures
Location Variability
Mean 474.8247 Std Deviation 20.05239
Median 476.0000 Variance 402.09815
Mode 440.0000 Range 105.00000
Interquartile Range 24.00000
Tests for Location: Mu0=0
Test -Statistic- -----p Value------
Student's t t 791.7501 Pr > |t| <.0001
Sign M 559 Pr >= |M| <.0001
Signed Rank S 312760.5 Pr >= |S| <.0001
Quantiles (Definition 5)
Quantile Estimate
100% Max 545
99% 525
95% 506
90% 500
75% Q3 488
50% Median 476
25% Q1 464
10% 440
5% 440
1% 440
0% Min 440
The UNIVARIATE Procedure
Variable: wattack (word attack posttest)
sfa = 0
Extreme Observations
----Lowest---- ----Highest---
Value Obs Value Obs
440 2327 532 1282
440 2323 532 1994
440 2322 537 1442
440 2320 545 1640
440 2312 545 1847
The UNIVARIATE Procedure
Variable: wattack (word attack posttest)
sfa = 1
Moments
N 1216 Sum Weights 1216
Mean 481.916118 Sum Observations 586010
Std Deviation 19.105112 Variance 365.005304
Skewness -0.2810488 Kurtosis -0.0585321
Uncorrected SS 282851146 Corrected SS 443481.444
Coeff Variation 3.9644061 Std Error Mean 0.54787666
Basic Statistical Measures
Location Variability
Mean 481.9161 Std Deviation 19.10511
Median 482.0000 Variance 365.00530
Mode 440.0000 Range 97.00000
Interquartile Range 23.00000
Tests for Location: Mu0=0
Test -Statistic- -----p Value------
Student's t t 879.6069 Pr > |t| <.0001
Sign M 608 Pr >= |M| <.0001
Signed Rank S 369968 Pr >= |S| <.0001
Quantiles (Definition 5)
Quantile Estimate
100% Max 537
99% 522
95% 511
90% 506
75% Q3 494
50% Median 482
25% Q1 471
10% 456
5% 440
1% 440
0% Min 440
The UNIVARIATE Procedure
Variable: wattack (word attack posttest)
sfa = 1
Extreme Observations
----Lowest---- ----Highest---
Value Obs Value Obs
440 1183 532 199
440 1169 532 310
440 1160 532 739
440 1147 532 1010
440 1130 537 1008
proc sort data = sfa;
by sfa;
run;
proc boxplot data=sfa;
plot wattack*sfa;
run;
Model #1 from Table 7.1 on page 114. Note that the estimates of the fixed effects are not identical to those in the text, but are very similar.
proc sort data=sfa;
by schid ;
run;
proc mixed data=sfa method=reml;
class schid;
model wattack = /solution ;
random schid;
run;
The Mixed Procedure
Model Information
Data Set WORK.SFA
Dependent Variable wattack
Covariance Structure Variance Components
Estimation Method REML
Residual Variance Method Profile
Fixed Effects SE Method Model-Based
Degrees of Freedom Method Containment
Class Level Information
Class Levels Values
schid 41 1 2 3 4 5 6 7 8 9 10 11 12 13
14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29 30 31 32 33
34 35 36 37 38 39 40 41
Dimensions
Covariance Parameters 2
Columns in X 1
Columns in Z 41
Subjects 1
Max Obs Per Subject 2334
Number of Observations
Number of Observations Read 2334
Number of Observations Used 2334
Number of Observations Not Used 0
Iteration History
Iteration Evaluations -2 Res Log Like Criterion
0 1 20578.22898221
1 3 20147.79602987 0.00000807
2 1 20147.72782562 0.00000009
3 1 20147.72708485 0.00000000
Convergence criteria met.
The Mixed Procedure
Covariance Parameter
Estimates
Cov Parm Estimate
schid 79.1290
Residual 314.19
Fit Statistics
-2 Res Log Likelihood 20147.7
AIC (smaller is better) 20151.7
AICC (smaller is better) 20151.7
BIC (smaller is better) 20155.2
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 477.54 1.4508 40 329.15 <.0001
Model #2 from Table 7.1 on page 114. Note that the estimates of the fixed effects are not identical to those in the text, but are very similar.
proc mixed data=sfa method=reml;
class schid;
model wattack = sfa /solution ;
random schid;
run;
The Mixed Procedure
Model Information
Data Set WORK.SFA
Dependent Variable wattack
Covariance Structure Variance Components
Estimation Method REML
Residual Variance Method Profile
Fixed Effects SE Method Model-Based
Degrees of Freedom Method Containment
Class Level Information
Class Levels Values
schid 41 1 2 3 4 5 6 7 8 9 10 11 12 13
14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29 30 31 32 33
34 35 36 37 38 39 40 41
Dimensions
Covariance Parameters 2
Columns in X 2
Columns in Z 41
Subjects 1
Max Obs Per Subject 2334
Number of Observations
Number of Observations Read 2334
Number of Observations Used 2334
Number of Observations Not Used 0
Iteration History
Iteration Evaluations -2 Res Log Like Criterion
0 1 20501.48291319
1 2 20141.47629690 0.00000008
2 1 20141.47565212 0.00000000
Convergence criteria met.
The Mixed Procedure
Covariance Parameter
Estimates
Cov Parm Estimate
schid 75.6802
Residual 314.23
Fit Statistics
-2 Res Log Likelihood 20141.5
AIC (smaller is better) 20145.5
AICC (smaller is better) 20145.5
BIC (smaller is better) 20148.9
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 475.30 2.0345 39 233.62 <.0001
sfa 4.3662 2.8437 2293 1.54 0.1248
Type 3 Tests of Fixed Effects
Num Den
Effect DF DF F Value Pr > F
sfa 1 2293 2.36 0.1248
Model #3 from Table 7.1 on page 114. The variable sch_ppvt is the within-school average of ppvt based on the full sample, rather than the subsample analyzed here, see footnote 15 on page 127.
proc mixed data=sfa method=reml;
class schid;
model wattack = sfa sch_ppvt /solution ;
random schid;
run;
The Mixed Procedure
Model Information
Data Set WORK.SFA
Dependent Variable wattack
Covariance Structure Variance Components
Estimation Method REML
Residual Variance Method Profile
Fixed Effects SE Method Model-Based
Degrees of Freedom Method Containment
Class Level Information
Class Levels Values
schid 41 1 2 3 4 5 6 7 8 9 10 11 12 13
14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29 30 31 32 33
34 35 36 37 38 39 40 41
Dimensions
Covariance Parameters 2
Columns in X 3
Columns in Z 41
Subjects 1
Max Obs Per Subject 2334
Number of Observations
Number of Observations Read 2334
Number of Observations Used 2334
Number of Observations Not Used 0
Iteration History
Iteration Evaluations -2 Res Log Like Criterion
0 1 20354.02113840
1 2 20127.21885957 0.00000001
Convergence criteria met.
The Mixed Procedure
Covariance Parameter
Estimates
Cov Parm Estimate
schid 49.2429
Residual 314.18
Fit Statistics
-2 Res Log Likelihood 20127.2
AIC (smaller is better) 20131.2
AICC (smaller is better) 20131.2
BIC (smaller is better) 20134.6
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 419.81 12.6327 38 33.23 <.0001
sfa 3.5695 2.3537 2293 1.52 0.1295
sch_ppvt 0.6229 0.1407 2293 4.43 <.0001
Type 3 Tests of Fixed Effects
Num Den
Effect DF DF F Value Pr > F
sfa 1 2293 2.30 0.1295
sch_ppvt 1 2293 19.61 <.0001
Model #3 using the within-school averages of prior ppvt score (new variable schavgppvt) from the analytic subsample instead of sch_ppvt. (Not shown in text, this analysis is mentioned in footnote 15 on page 127.)
proc sql ;
create table sfa as
select *, mean(ppvt) as schavgppvt
from sfa
group by schid;
quit;
proc mixed data=sfa method=reml;
class schid;
model wattack = sfa schavgppvt /solution ;
random schid;
run;
The Mixed Procedure
Model Information
Data Set WORK.SFA
Dependent Variable wattack
Covariance Structure Variance Components
Estimation Method REML
Residual Variance Method Profile
Fixed Effects SE Method Model-Based
Degrees of Freedom Method Containment
Class Level Information
Class Levels Values
schid 41 1 2 3 4 5 6 7 8 9 10 11 12 13
14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29 30 31 32 33
34 35 36 37 38 39 40 41
Dimensions
Covariance Parameters 2
Columns in X 3
Columns in Z 41
Subjects 1
Max Obs Per Subject 2334
Number of Observations
Number of Observations Read 2334
Number of Observations Used 2334
Number of Observations Not Used 0
Iteration History
Iteration Evaluations -2 Res Log Like Criterion
0 1 20338.04927507
1 2 20126.12066409 0.00000013
2 1 20126.11963668 0.00000000
Convergence criteria met.
The Mixed Procedure
Covariance Parameter
Estimates
Cov Parm Estimate
schid 47.4401
Residual 314.19
Fit Statistics
-2 Res Log Likelihood 20126.1
AIC (smaller is better) 20130.1
AICC (smaller is better) 20130.1
BIC (smaller is better) 20133.5
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 421.60 11.6898 39 36.07 <.0001
sfa 3.2159 2.3231 2292 1.38 0.1664
schavgppvt 0.6024 0.1299 2292 4.64 <.0001
Type 3 Tests of Fixed Effects
Num Den
Effect DF DF F Value Pr > F
sfa 1 2292 1.92 0.1664
schavgppvt 1 2292 21.49 <.0001
The following models show various ways of controlling for individual- and school-level ppvt. None of the models shown below are displayed in the text.
Controlling for individual-level ppvt, deviated from the grand mean (new variable ppvt_devgm).
proc means data=sfa;
vars ppvt;
run;
The MEANS Procedure
Analysis Variable : ppvt ppvt pretest
N Mean Std Dev Minimum Maximum
2334 90.4005998 15.0008207 40.0000000 144.0000000
data sfa;
set sfa;
ppvt_devgm = ppvt-90.4005998;
run;
proc mixed data=sfa method=reml;
class schid;
model wattack = sfa ppvt_devgm /solution ;
random schid;
run;
The Mixed Procedure
Model Information
Data Set WORK.SFA
Dependent Variable wattack
Covariance Structure Variance Components
Estimation Method REML
Residual Variance Method Profile
Fixed Effects SE Method Model-Based
Degrees of Freedom Method Containment
Class Level Information
Class Levels Values
schid 41 1 2 3 4 5 6 7 8 9 10 11 12 13
14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29 30 31 32 33
34 35 36 37 38 39 40 41
Dimensions
Covariance Parameters 2
Columns in X 3
Columns in Z 41
Subjects 1
Max Obs Per Subject 2334
Number of Observations
Number of Observations Read 2334
Number of Observations Used 2334
Number of Observations Not Used 0
Iteration History
Iteration Evaluations -2 Res Log Like Criterion
0 1 20110.44100068
1 2 19862.58772768 0.00000014
2 1 19862.58665957 0.00000000
Convergence criteria met.
The Mixed Procedure
Covariance Parameter
Estimates
Cov Parm Estimate
schid 47.8823
Residual 279.73
Fit Statistics
-2 Res Log Likelihood 19862.6
AIC (smaller is better) 19866.6
AICC (smaller is better) 19866.6
BIC (smaller is better) 19870.0
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 475.91 1.6454 39 289.24 <.0001
sfa 3.4402 2.3006 2292 1.50 0.1350
ppvt_devgm 0.4852 0.02781 2292 17.45 <.0001
Type 3 Tests of Fixed Effects
Num Den
Effect DF DF F Value Pr > F
sfa 1 2292 2.24 0.1350
ppvt_devgm 1 2292 304.38 <.0001
Controlling for individual-level ppvt by including deviations of individual scores from school-average scores (new variable ppvt_devsm) and school-average scores from the grand mean (new variable schavgppvt_devgm).
data sfa;
set sfa;
ppvt_devsm = ppvt-schavgppvt;
schavgppvt_devgm = schavgppvt-90.4006;
run;
proc mixed data=sfa method=reml;
class schid;
model wattack = sfa ppvt_devsm schavgppvt_devgm /solution ;
random schid;
run;
The Mixed Procedure
Model Information
Data Set WORK.SFA
Dependent Variable wattack
Covariance Structure Variance Components
Estimation Method REML
Residual Variance Method Profile
Fixed Effects SE Method Model-Based
Degrees of Freedom Method Containment
Class Level Information
Class Levels Values
schid 41 1 2 3 4 5 6 7 8 9 10 11 12 13
14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29 30 31 32 33
34 35 36 37 38 39 40 41
Dimensions
Covariance Parameters 2
Columns in X 4
Columns in Z 41
Subjects 1
Max Obs Per Subject 2334
Number of Observations
Number of Observations Read 2334
Number of Observations Used 2334
Number of Observations Not Used 0
Iteration History
Iteration Evaluations -2 Res Log Like Criterion
0 1 20109.23720784
1 2 19863.92245580 0.00000018
2 1 19863.92105409 0.00000000
Convergence criteria met.
The Mixed Procedure
Covariance Parameter
Estimates
Cov Parm Estimate
schid 48.1678
Residual 279.72
Fit Statistics
-2 Res Log Likelihood 19863.9
AIC (smaller is better) 19867.9
AICC (smaller is better) 19867.9
BIC (smaller is better) 19871.3
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 476.06 1.6581 39 287.11 <.0001
sfa 3.1892 2.3223 2291 1.37 0.1698
ppvt_devsm 0.4795 0.02847 2291 16.84 <.0001
schavgppvt_devgm 0.6030 0.1299 2291 4.64 <.0001
Type 3 Tests of Fixed Effects
Num Den
Effect DF DF F Value Pr > F
sfa 1 2291 1.89 0.1698
ppvt_devsm 1 2291 283.58 <.0001
schavgppvt_devgm 1 2291 21.56 <.0001
Controlling for school-average ppvt deviated from the grand mean (schavgppvt_devgm).
proc mixed data=sfa method=reml;
class schid;
model wattack = sfa schavgppvt_devgm /solution ;
random schid;
run;
The Mixed Procedure
Model Information
Data Set WORK.SFA
Dependent Variable wattack
Covariance Structure Variance Components
Estimation Method REML
Residual Variance Method Profile
Fixed Effects SE Method Model-Based
Degrees of Freedom Method Containment
Class Level Information
Class Levels Values
schid 41 1 2 3 4 5 6 7 8 9 10 11 12 13
14 15 16 17 18 19 20 21 22 23
24 25 26 27 28 29 30 31 32 33
34 35 36 37 38 39 40 41
Dimensions
Covariance Parameters 2
Columns in X 3
Columns in Z 41
Subjects 1
Max Obs Per Subject 2334
Number of Observations
Number of Observations Read 2334
Number of Observations Used 2334
Number of Observations Not Used 0
Iteration History
Iteration Evaluations -2 Res Log Like Criterion
0 1 20338.04927507
1 2 20126.12066409 0.00000013
2 1 20126.11963668 0.00000000
Convergence criteria met.
The Mixed Procedure
Covariance Parameter
Estimates
Cov Parm Estimate
schid 47.4401
Residual 314.19
Fit Statistics
-2 Res Log Likelihood 20126.1
AIC (smaller is better) 20130.1
AICC (smaller is better) 20130.1
BIC (smaller is better) 20133.5
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 476.06 1.6584 39 287.06 <.0001
sfa 3.2159 2.3231 2292 1.38 0.1664
schavgppvt_devgm 0.6024 0.1299 2292 4.64 <.0001
Type 3 Tests of Fixed Effects
Num Den
Effect DF DF F Value Pr > F
sfa 1 2292 1.92 0.1664
schavgppvt_devgm 1 2292 21.49 <.0001
