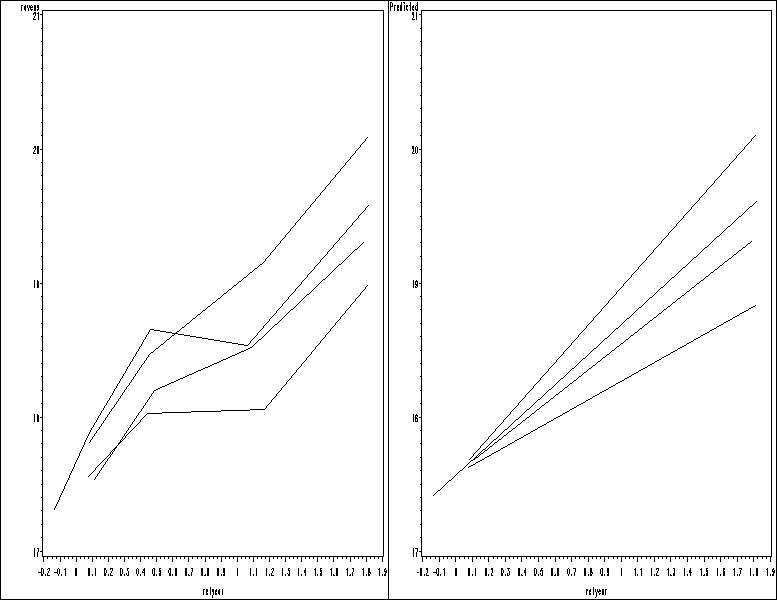Table 7.2, page 182.
Log base 2 scale only.
proc mixed data = pain method= reml noitprint noclprint noinfo;
class id cs trial;
model l2paintol = cs / solution notest;
repeated trial/ subject = id type = unstructured;
run;
The Mixed Procedure
Covariance Parameter Estimates
Cov Parm Subject Estimate
UN(1,1) id 1.0065
UN(2,1) id 0.7482
UN(2,2) id 1.1281
UN(3,1) id 0.9522
UN(3,2) id 0.8736
UN(3,3) id 1.3423
UN(4,1) id 0.6725
UN(4,2) id 0.7908
UN(4,3) id 1.0022
UN(4,4) id 1.3071
Fit Statistics
-2 Res Log Likelihood 568.4
AIC (smaller is better) 588.4
AICC (smaller is better) 589.4
BIC (smaller is better) 610.0
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
9 170.12 <.0001
Solution for Fixed Effects
coping Standard
Effect style Estimate Error DF t Value Pr > |t|
Intercept 5.0770 0.1620 62 31.35 <.0001
cs attender -0.5054 0.2291 62 -2.21 0.0311
cs distracter 0 . . . .
Table 7.3, page 184.
NOTE: The downloadable dataset "cognitive" does not match the one used for this analysis. The author was contacted and provided this version of the cognitive dataset: https://stats.idre.ucla.edu/wp-content/uploads/2016/02/cognitive_v2.sas7bdat .
proc mixed data = cognitive_v2 method= reml noitprint noclprint ;
class id sex;
model ravens = sex ses / solution notest;
repeated / type=sp(pow)(relyear) subject=id;
run;
The Mixed Procedure
Model Information
Data Set WORK.COGNITIVE
Dependent Variable RAVENS
Covariance Structure Spatial Power
Subject Effect ID
Estimation Method REML
Residual Variance Method Profile
Fixed Effects SE Method Model-Based
Degrees of Freedom Method Between-Within
Dimensions
Covariance Parameters 2
Columns in X 4
Columns in Z 0
Subjects 529
Max Obs Per Subject 5
Number of Observations
Number of Observations Read 2533
Number of Observations Used 2498
Number of Observations Not Used 35
Covariance Parameter Estimates
Cov Parm Subject Estimate
SP(POW) ID 0.04977
Residual 8.8771
Fit Statistics
-2 Res Log Likelihood 12290.3
AIC (smaller is better) 12294.3
AICC (smaller is better) 12294.3
BIC (smaller is better) 12302.9
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
1 163.87 <.0001
Solution for Fixed Effects
Standard
Effect SEX Estimate Error DF t Value Pr > |t|
Intercept 17.5755 0.2761 526 63.65 <.0001
SEX boy 0.6223 0.1461 526 4.26 <.0001
SEX girl 0 . . . .
ses 0.006100 0.003066 526 1.99 0.0472
Table 7.4, page 188.
Results for the first four columns only.
data weight;
set weight1;
week_cont = week;
run;
proc means data = weight n mean;
class week;
var weight;
run;
The MEANS Procedure
Analysis Variable : weight
N
week Obs N Mean
------------------------------------------
1 38 38 192.7815789
2 38 38 193.5631579
3 38 38 190.9342105
4 38 38 187.9605263
5 38 33 185.8484848
6 38 31 190.8064516
7 38 25 188.4080000
8 38 24 190.3333333
------------------------------------------
proc mixed data = weight method = reml noitprint noinfo noclprint;
class id week;
model weight = week / solution notest noint;
repeated week/ subject = id type =cs;
random intercept week_cont/ subject=id type = un;
run;
[...output omitted...]
Solution for Fixed Effects
Standard
Effect week Estimate Error DF t Value Pr > |t|
week 1 192.78 4.1996 183 45.91 <.0001
week 2 193.56 4.1693 183 46.43 <.0001
week 3 190.93 4.1427 183 46.09 <.0001
week 4 187.96 4.1198 183 45.62 <.0001
week 5 186.64 4.1028 183 45.49 <.0001
week 6 188.11 4.0892 183 46.00 <.0001
week 7 186.90 4.0833 183 45.77 <.0001
week 8 185.34 4.0791 183 45.44 <.0001
Table 7.5, page 190.
proc mixed data = weight method = reml noitprint noinfo noclprint;
class id week;
model weight = week / notest noint;
repeated week/ subject = id type =cs;
random intercept week_cont/ subject=id type = cs;
estimate "2 vs 1" week -1 1 0 0 0 0 0 0;
estimate "3 vs 1" week -1 0 1 0 0 0 0 0;
estimate "4 vs 1" week -1 0 0 1 0 0 0 0;
estimate "5 vs 1" week -1 0 0 0 1 0 0 0;
estimate "6 vs 1" week -1 0 0 0 0 1 0 0;
estimate "7 vs 1" week -1 0 0 0 0 0 1 0;
estimate "8 vs 1" week -1 0 0 0 0 0 0 1;
estimate "2 vs 1" week -1 1 0 0 0 0 0 0;
estimate "3 vs 2" week 0 -1 1 0 0 0 0 0;
estimate "4 vs 3" week 0 0 -1 1 0 0 0 0;
estimate "5 vs 4" week 0 0 0 -1 1 0 0 0;
estimate "6 vs 5" week 0 0 0 0 -1 1 0 0;
estimate "7 vs 6" week 0 0 0 0 0 -1 1 0;
estimate "8 vs 7" week 0 0 0 0 0 0 -1 1;
run;
The Mixed Procedure
Covariance Parameter Estimates
Cov Parm Subject Estimate
Variance id 6.3352
CS id -5.7264
CS id 677.34
Residual 3.0679
Fit Statistics
-2 Res Log Likelihood 1383.9
AIC (smaller is better) 1391.9
AICC (smaller is better) 1392.1
BIC (smaller is better) 1398.5
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
3 1038.02 <.0001
Estimates
Standard
Label Estimate Error DF t Value Pr > |t|
2 vs 1 0.7816 0.4213 183 1.86 0.0652
3 vs 1 -1.8474 0.4749 183 -3.89 0.0001
4 vs 1 -4.8211 0.5529 183 -8.72 <.0001
5 vs 1 -6.1440 0.6601 183 -9.31 <.0001
6 vs 1 -4.6689 0.7703 183 -6.06 <.0001
7 vs 1 -5.8820 0.9024 183 -6.52 <.0001
8 vs 1 -7.4452 1.0244 183 -7.27 <.0001
2 vs 1 0.7816 0.4213 183 1.86 0.0652
3 vs 2 -2.6289 0.4213 183 -6.24 <.0001
4 vs 3 -2.9737 0.4213 183 -7.06 <.0001
5 vs 4 -1.3229 0.4420 183 -2.99 0.0031
6 vs 5 1.4750 0.4671 183 3.16 0.0019
7 vs 6 -1.2131 0.5130 183 -2.36 0.0191
8 vs 7 -1.5632 0.5435 183 -2.88 0.0045
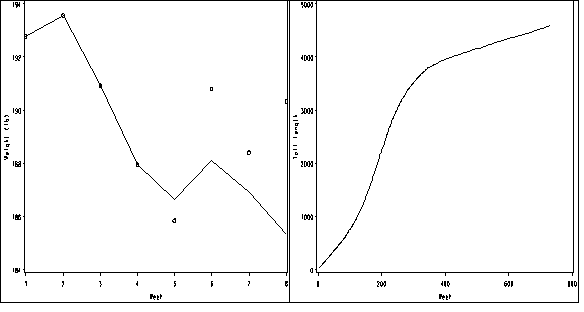
Figure 7.3 (a), page 191.
Note Figure 7.3(b)-(c) are hypothetical data. Hence, they are not reproduced.
proc mixed data = weight method = reml noitprint noinfo noclprint;
class id week;
model weight = week / notest noint outpredm=pred_weight;
repeated week/ subject = id type =cs;
random intercept week_cont/ subject=id type = cs;
run;
proc sql;
create table summary_means as
select week,
mean(weight) as sample_mean,
mean(pred) as pred_mean
from pred_weight
group by week;
quit;
goptions reset = all;
symbol1 value=circle color=black;
symbol2 value=none interpol = join repeat = 1;
axis1 order =(1 to 8 by 1) label=(a=0 'Week') minor=none;
axis2 order =(184 to 194 by 2) label = (a=90 'Weight (lb)') minor=none ;
proc gplot data = summary_means;
plot (sample_mean pred_mean)*week /overlay haxis=axis1 vaxis=axis2 name = 'f7_3a';
run; quit;
proc loess data=wallaby;
model tail=agedays /smooth=0.4;
ods output OutputStatistics=smoothed_mean;
run; quit;
proc sort data = smoothed_mean;
by agedays;
run;
goptions reset = all;
symbol1 value=none interpol=join r=1;
axis1 order =(0 to 800 by 200) label=(a=0 'Week') minor=none;
axis2 order =(0 to 5000 by 1000) value = ('0' '1000' '2000' '3000' '4000' '5000')
label = (a=90 'Tail length') minor=none ;
proc gplot data = smoothed_mean;
plot pred*agedays/ haxis=axis1 vaxis=axis2 name = 'f7_3d';
run; quit;
proc greplay igout = work.gseg tc=sashelp.templt template=h2 nofs;
treplay 1:f7_3a 2:f7_3d;
run; quit;
Table 7.6, page 199.
data pain1;
set pain;
tmt_a = (treatment = "attend")*(trial = 4);
tmt_d = (treatment = "distract")*(trial = 4);
tmt_n = (treatment = "no directions")*(trial = 4);
distracter = (cs = "distracter");
run;
proc mixed data = pain1 method = reml noinfo noclprint noitprint;
class id trial;
model l2paintol = distracter tmt_a tmt_d tmt_n/ solution notest ;
repeated trial / subject = id type = cs;
estimate 'treatment d-a' tmt_d 1 tmt_a -1;
estimate 'treatment d-n' tmt_d 1 tmt_n -1;
estimate 'treatment a-n' tmt_a 1 tmt_n -1;
estimate 'ab' intercept 1;
estimate 'db' intercept 1 distracter 1;
estimate 'aa' intercept 1 tmt_a 1;
estimate 'ad' intercept 1 tmt_d 1;
estimate 'an' intercept 1 tmt_n 1;
estimate 'da' intercept 1 distracter 1 tmt_a 1;
estimate 'dd' intercept 1 distracter 1 tmt_d 1;
estimate 'dn' intercept 1 distracter 1 tmt_n 1;
run;
The Mixed Procedure
Covariance Parameter Estimates
Cov Parm Subject Estimate
CS id 0.8149
Residual 0.3485
Fit Statistics
-2 Res Log Likelihood 587.5
AIC (smaller is better) 591.5
AICC (smaller is better) 591.5
BIC (smaller is better) 595.8
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
1 146.69 <.0001
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 4.5436 0.1701 62 26.71 <.0001
distracter 0.4545 0.2385 62 1.91 0.0613
tmt_a -0.1217 0.1508 178 -0.81 0.4206
tmt_d 0.3203 0.1472 178 2.18 0.0309
tmt_n -0.2922 0.1525 178 -1.92 0.0569
Estimates
Standard
Label Estimate Error DF t Value Pr > |t|
treatment d-a 0.4421 0.2096 178 2.11 0.0364
treatment d-n 0.6126 0.2108 178 2.91 0.0041
treatment a-n 0.1705 0.2133 178 0.80 0.4251
ab 4.5436 0.1701 62 26.71 <.0001
db 4.9980 0.1699 62 29.42 <.0001
aa 4.4218 0.2191 178 20.18 <.0001
ad 4.8639 0.2170 178 22.41 <.0001
an 4.2513 0.2198 178 19.34 <.0001
da 4.8763 0.2190 178 22.27 <.0001
dd 5.3184 0.2161 178 24.61 <.0001
dn 4.7058 0.2190 178 21.49 <.0001
Table 7.7, page 200.
data pain2;
set pain1;
tmt = "Z";
if trial = 4 and treatment = "attend" then tmt = "A";
if trial = 4 and treatment = "distract" then tmt = "D";
if trial = 4 and treatment = "no directions" then tmt = "N";
run;
proc mixed data = pain2 method = reml noinfo noclprint noitprint;
class id trial cs tmt ;
model l2paintol = cs tmt / solution corrb notest ;
repeated trial/ subject = id type = cs;
run;
The Mixed Procedure
Covariance Parameter Estimates
Cov Parm Subject Estimate
CS id 0.8149
Residual 0.3485
Fit Statistics
-2 Res Log Likelihood 587.5
AIC (smaller is better) 591.5
AICC (smaller is better) 591.5
BIC (smaller is better) 595.8
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
1 146.69 <.0001
Solution for Fixed Effects
coping Standard
Effect style tmt Estimate Error DF t Value Pr > |t|
Intercept 4.9980 0.1699 62 29.42 <.0001
cs attender -0.4545 0.2385 62 -1.91 0.0613
cs distracter 0 . . . .
tmt A -0.1217 0.1508 58 -0.81 0.4228
tmt D 0.3203 0.1472 58 2.18 0.0336
tmt N -0.2922 0.1525 58 -1.92 0.0602
tmt Z 0 . . . .
Correlation Matrix for Fixed Effects
coping
Row Effect style tmt Col1 Col2 Col3 Col4 Col5 Col6
1 Intercept 1.0000 -0.7010 -0.07142 -0.07654 -0.08005
2 cs attender -0.7010 1.0000 -0.00012 0.004686 0.003969
3 cs distracter 1.0000
4 tmt A -0.07142 -0.00012 1.0000 0.01030 0.01086
5 tmt D -0.07654 0.004686 0.01030 1.0000 0.01115
6 tmt N -0.08005 0.003969 0.01086 0.01115 1.0000
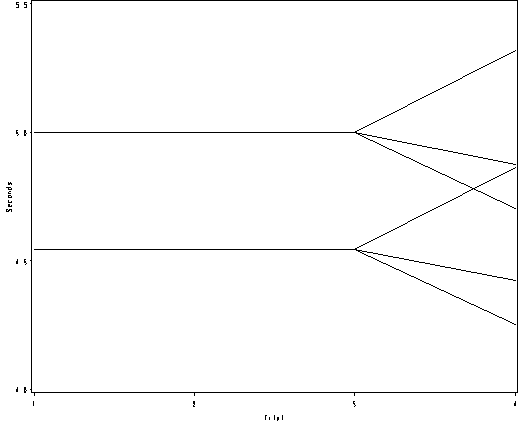
Figure 7.5(a), page 201.
Note y-axis in the graph is not back transformed.
proc mixed data = pain2 method = reml noinfo noclprint noitprint; class id trial; model l2paintol = distracter tmt_a tmt_d tmt_n/ solution notest outpredm=pain_pred; repeated trial / subject = id type = cs; run; proc sql; create table pain_mean as select trial, distracter, treatment, mean(pred) as pred_mean from pain_pred group by trial, distracter, treatment; quit; data pain_mean; set pain_mean; dt = distracter || treatment; proc print; run; goptions reset = all; symbol1 value=none color = black interpol=join r=6; axis1 order =(1 2 3 4) label=(a=0 'Trial') minor=none; axis2 order =(4 to 5.5 by .5) label = (a=90 'Seconds') minor=none ; proc gplot data = pain_mean; plot pred_mean*trial =dt /haxis=axis1 vaxis = axis2 nolegend; run; quit;
Table 7.8, page 204.
data pain3;
set pain2;
attend = (cs = "attender");
run;
proc mixed data = pain3 method = reml noinfo noclprint noitprint ;
class id trial;
model l2paintol = attend tmt_a tmt_d tmt_n attend*tmt_a attend*tmt_d attend*tmt_n/ solution notest;
repeated trial / subject = id type = cs;
*Second section;
estimate 'tmt aa' tmt_a 1 attend*tmt_a 1 ;
estimate 'tmt ad' tmt_d 1 attend*tmt_d 1;
estimate 'tmt an' tmt_n 1 attend*tmt_n 1;
estimate 'tmt da' tmt_a 1;
estimate 'tmt dd' tmt_d 1;
estimate 'tmt dn' tmt_n 1;
*Third section;
estimate 'tmt a da' tmt_d 1 attend*tmt_d 1 tmt_a -1 attend*tmt_a -1;
estimate 'tmt a dn' tmt_d 1 attend*tmt_d 1 tmt_n -1 attend*tmt_n -1;
estimate 'tmt a an' tmt_a 1 attend*tmt_a 1 tmt_n -1 attend*tmt_n -1;
estimate 'tmt d da' tmt_d 1 tmt_a -1;
estimate 'tmt d dn' tmt_d 1 tmt_n -1;
estimate 'tmt d an' tmt_a 1 tmt_n -1;
*Fourth section;
estimate 'ab' intercept 1 attend 1;
estimate 'db' intercept 1;
*Fifth section;
estimate 'aa' intercept 1 attend 1 tmt_a 1 attend*tmt_a 1;
estimate 'ad' intercept 1 attend 1 tmt_d 1 attend*tmt_d 1;
estimate 'an' intercept 1 attend 1 tmt_n 1 attend*tmt_n 1;
estimate 'da' intercept 1 tmt_a 1;
estimate 'dd' intercept 1 tmt_d 1;
estimate 'dn' intercept 1 tmt_n 1;
ods output Estimates = est;
run;
The Mixed Procedure
Covariance Parameter Estimates
Cov Parm Subject Estimate
CS id 0.7937
Residual 0.3432
Fit Statistics
-2 Res Log Likelihood 581.9
AIC (smaller is better) 585.9
AICC (smaller is better) 586.0
BIC (smaller is better) 590.3
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
1 142.92 <.0001
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 5.0106 0.1692 62 29.62 <.0001
attend -0.4780 0.2393 62 -2.00 0.0502
tmt_a -0.3518 0.2116 175 -1.66 0.0982
tmt_d 0.5761 0.2019 175 2.85 0.0048
tmt_n -0.4818 0.2154 175 -2.24 0.0266
attend*tmt_a 0.4599 0.2993 175 1.54 0.1261
attend*tmt_d -0.5371 0.2924 175 -1.84 0.0680
attend*tmt_n 0.3736 0.3027 175 1.23 0.2187
Estimates
Standard
Label Estimate Error DF t Value Pr > |t|
tmt aa 0.1082 0.2116 175 0.51 0.6098
tmt ad 0.03895 0.2116 175 0.18 0.8542
tmt an -0.1082 0.2126 175 -0.51 0.6114
tmt da -0.3518 0.2116 175 -1.66 0.0982
tmt dd 0.5761 0.2019 175 2.85 0.0048
tmt dn -0.4818 0.2154 175 -2.24 0.0266
tmt a da -0.06924 0.2977 175 -0.23 0.8164
tmt a dn 0.1472 0.2984 175 0.49 0.6225
tmt a an 0.2164 0.2984 175 0.73 0.4693
tmt d da 0.9278 0.2909 175 3.19 0.0017
tmt d dn 1.0579 0.2934 175 3.61 0.0004
tmt d an 0.1301 0.3002 175 0.43 0.6653
ab 4.5326 0.1693 62 26.77 <.0001
db 5.0106 0.1692 62 29.62 <.0001
aa 4.6408 0.2573 175 18.03 <.0001
ad 4.5715 0.2573 175 17.77 <.0001
an 4.4244 0.2576 175 17.18 <.0001
da 4.6589 0.2573 175 18.11 <.0001
dd 5.5867 0.2493 175 22.41 <.0001
dn 4.5288 0.2584 175 17.53 <.0001
Figure 7.6, page 205.
Note: Order of horizontal axis here does not match that in book.
data est2; set est;
where label in ("ab" "aa" "ad" "an" "db" "da" "dd" "dn");
Est_new = 2**Estimate;
CI_lower = Estimate - 1.9934627*(StdErr);
CI_upper = Estimate + 1.9934627*(StdErr);
CI_lnew = 2**CI_lower;
CI_unew = 2**CI_upper;
keep label CI_lnew CI_unew Est_new;
run;
data est3; set est2;
hilo = CI_lnew; output;
hilo = CI_unew; output;
drop CI_lnew CI_unew;
run;
goptions reset=all border;
symbol1 i=hilo v=dot c=blue;
symbol2 i=none v=dot c=white;
symbol3 i=none v=circle c=red;
axis1 offset=(2,2);
proc gplot data=est3;
plot Est_new*label hilo*label hilo*label / overlay haxis=axis1;
run;
quit;
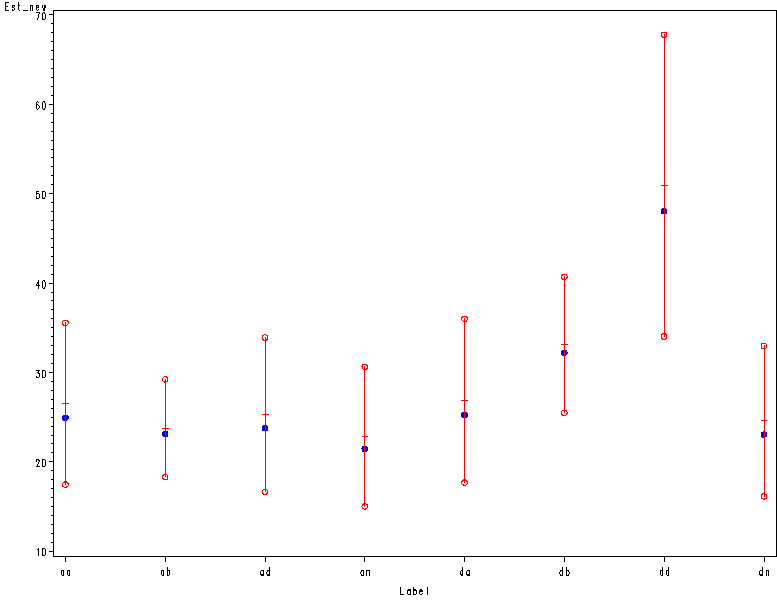
Table 7.9, page 210.
*Model (a);
proc mixed data = cognitive method= ml noinfo noclprint noitprint;
class id;
model ravens = relmonth / solution notest;
repeated / subject = id type = sp(pow)(relyear);
run;
The Mixed Procedure
Covariance Parameter Estimates
Cov Parm Subject Estimate
SP(POW) id 0.05432
Residual 8.7852
Fit Statistics
-2 Log Likelihood 12731.6
AIC (smaller is better) 12739.6
AICC (smaller is better) 12739.6
BIC (smaller is better) 12756.8
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
1 171.13 <.0001
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 17.5635 0.1007 545 174.45 <.0001
relmonth 0.08706 0.007595 2051 11.46 <.0001
*Model (b);
proc mixed data = cognitive method= ml noinfo noclprint noitprint ;
class id sex;
model ravens = sex relmonth / solution notest;
repeated / subject = id type = sp(pow)(relyear);
run;
The Mixed Procedure
Covariance Parameter Estimates
Cov Parm Subject Estimate
SP(POW) id 0.05120
Residual 8.6928
Fit Statistics
-2 Log Likelihood 12714.0
AIC (smaller is better) 12724.0
AICC (smaller is better) 12724.0
BIC (smaller is better) 12745.5
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
1 164.49 <.0001
Solution for Fixed Effects
Standard
Effect sex Estimate Error DF t Value Pr > |t|
Intercept 17.2546 0.1239 544 139.29 <.0001
sex boy 0.5978 0.1416 544 4.22 <.0001
sex girl 0 . . . .
relmonth 0.08674 0.007547 2051 11.49 <.0001
*Model (c);
proc mixed data = cognitive method= ml noinfo noclprint noitprint ;
class id sex;
model ravens = relmonth relmonth*sex/ solution notest;
repeated / subject = id type = sp(pow)(relyear);
run;
The Mixed Procedure
Covariance Parameter Estimates
Cov Parm Subject Estimate
SP(POW) id 0.05166
Residual 8.7010
Fit Statistics
-2 Log Likelihood 12714.9
AIC (smaller is better) 12724.9
AICC (smaller is better) 12725.0
BIC (smaller is better) 12746.5
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
1 166.81 <.0001
Solution for Fixed Effects
Standard
Effect sex Estimate Error DF t Value Pr > |t|
Intercept 17.5655 0.09990 545 175.83 <.0001
relmonth 0.06376 0.009443 2050 6.75 <.0001
relmonth*sex boy 0.04394 0.01072 2050 4.10 <.0001
relmonth*sex girl 0 . . . .
*Model (d);
proc mixed data = cognitive method= ml noinfo noclprint noitprint ;
class id sex;
model ravens = sex|relmonth / solution notest;
repeated / subject = id type = sp(pow)(relyear);
run;
The Mixed Procedure
Covariance Parameter Estimates
Cov Parm Subject Estimate
SP(POW) id 0.05105
Residual 8.6828
Fit Statistics
-2 Log Likelihood 12711.4
AIC (smaller is better) 12723.4
AICC (smaller is better) 12723.5
BIC (smaller is better) 12749.3
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
1 164.12 <.0001
Solution for Fixed Effects
Standard
Effect sex Estimate Error DF t Value Pr > |t|
Intercept 17.3710 0.1439 544 120.72 <.0001
sex boy 0.3744 0.1996 544 1.88 0.0612
sex girl 0 . . . .
relmonth 0.07415 0.01094 2050 6.78 <.0001
relmonth*sex boy 0.02397 0.01510 2050 1.59 0.1127
relmonth*sex girl 0 . . . .
Table 7.10, page 213.
data cog;
set in.cognitive;
newtmt = treatment;
if relyear <0 then newtmt = "control";
run;
proc mixed data = cog method= reml noclprint noitprint noinfo;
class id newtmt ;
model ravens = relmonth relmonth*newtmt / solution notest outpred = cogp;
repeated / subject = id type = sp(pow)(relyear);
estimate 'meat' relmonth 1 newtmt*relmonth 0 0 1 0;
estimate 'control' relmonth 1 newtmt*relmonth 0 1 0 0;
estimate 'calorie' relmonth 1 newtmt*relmonth 1 0 0 0;
estimate 'milk' relmonth 1 newtmt*relmonth 0 0 0 1;
estimate 'meat-control' newtmt*relmonth 0 -1 1 0;
estimate 'meat-calorie' newtmt*relmonth -1 0 1 0;
estimate 'meat-milk' newtmt*relmonth 0 0 1 -1;
estimate 'control-calorie' newtmt*relmonth -1 1 0 0;
estimate 'control-milk' newtmt*relmonth 0 1 0 -1;
estimate 'calorie-milk' newtmt*relmonth 1 0 0 -1;
run;
The Mixed Procedure
Covariance Parameter Estimates
Cov Parm Subject Estimate
SP(POW) id 0.05247
Residual 8.7308
Fit Statistics
-2 Res Log Likelihood 12748.0
AIC (smaller is better) 12752.0
AICC (smaller is better) 12752.0
BIC (smaller is better) 12760.6
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
1 168.10 <.0001
Solution for Fixed Effects
Standard
Effect newtmt Estimate Error DF t Value Pr > |t|
Intercept 17.5702 0.1005 545 174.77 <.0001
relmonth 0.05816 0.01191 2048 4.88 <.0001
relmonth*newtmt calorie 0.02314 0.01490 2048 1.55 0.1205
relmonth*newtmt control 0.03547 0.01524 2048 2.33 0.0201
relmonth*newtmt meat 0.05843 0.01523 2048 3.84 0.0001
relmonth*newtmt milk 0 . . . .
Estimates
Standard
Label Estimate Error DF t Value Pr > |t|
meat 0.1166 0.01233 2048 9.45 <.0001
control 0.09363 0.01185 2048 7.90 <.0001
calorie 0.08130 0.01198 2048 6.79 <.0001
milk 0.05816 0.01191 2048 4.88 <.0001
meat-control 0.02297 0.01557 2048 1.48 0.1402
meat-calorie 0.03529 0.01523 2048 2.32 0.0206
meat-milk 0.05843 0.01523 2048 3.84 0.0001
control-calorie 0.01232 0.01526 2048 0.81 0.4194
control-milk 0.03547 0.01524 2048 2.33 0.0201
calorie-milk 0.02314 0.01490 2048 1.55 0.1205
Figure 7.8, page 213.
* (a); goptions reset = all; symbol1 value=none color = black interpol=join r=6; proc sort data = cog; by newtmt rn; run; proc means data = cog; by newtmt rn; var ravens relyear; output out = mean_rav; run; data means2; set mean_rav; where _STAT_ = "MEAN"; run; proc gplot data = means2; plot ravens*relyear = newtmt / nolegend name = 'f78_a'; run; quit; * (b); goptions reset = all; symbol1 value=none color = black interpol=join r=6; proc sort data = cogp; by newtmt rn; run; proc means data = cogp; by newtmt rn; var pred relyear; output out = mean_rav; run; data means2; set mean_rav; where _STAT_ = "MEAN"; run; proc gplot data = means2; plot pred*relyear = newtmt / nolegend name = 'f78_b'; run; quit; proc greplay igout = work.gseg tc=sashelp.templt template=h2 nofs; treplay 1:f78_a 2:f78_b; run; quit;
Table 7.11, page 217.
proc mixed data=cognitive method=reml covtest noitprint noclprint;
class id;
model ravens =age_at_time0 relyear / solution notest;
repeated / type=sp(pow)(relyear) subject=id;
estimate 'Age - time' relyear -1 age_at_time0 1 ;
run;
The Mixed Procedure
Model Information
Data Set COGNITIVE
Dependent Variable ravens
Covariance Structure Spatial Power
Subject Effect id
Estimation Method REML
Residual Variance Method Profile
Fixed Effects SE Method Model-Based
Degrees of Freedom Method Between-Within
Dimensions
Covariance Parameters 2
Columns in X 3
Columns in Z 0
Subjects 542
Max Obs Per Subject 5
Number of Observations
Number of Observations Read 2730
Number of Observations Used 2593
Number of Observations Not Used 137
Covariance Parameter Estimates
Standard Z
Cov Parm Subject Estimate Error Value Pr Z
SP(POW) id 0.05258 0.01002 5.25 <.0001
Residual 8.7454 0.2653 32.96 <.0001
Fit Statistics
-2 Res Log Likelihood 12707.8
AIC (smaller is better) 12711.8
AICC (smaller is better) 12711.8
BIC (smaller is better) 12720.4
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
1 168.26 <.0001
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 16.4041 0.4137 540 39.65 <.0001
age_at_time0 0.1515 0.05278 540 2.87 0.0043
relyear 1.0464 0.09101 2050 11.50 <.0001
Estimates
Standard
Label Estimate Error DF t Value Pr > |t|
Age - time -0.8949 0.1055 540 -8.48 <.0001
Figure 7.9, page 218.
proc mixed data=cognitive method=reml covtest noitprint noclprint; class id; model ravens = female morbcut relyear female*morbcut female*relyear morbcut*relyear female*morbcut*relyear / solution notest outpred = cogp2; random Intercept / subject=id; run; data cogp2; set cogp2; if sex = "girl" and morbcut = 0 then sex_morb = 1; else if sex = "girl" and morbcut = 1 then sex_morb = 2; else if sex = "boy" and morbcut = 0 then sex_morb = 3; else if sex = "boy" and morbcut = 1 then sex_morb = 4; run; proc freq data = cogp2; table sex_morb; run; * (a); goptions reset = all; symbol1 value=none color = black interpol=join r=6; proc sort data = cogp2; by sex_morb rn; run; proc means data = cogp2; by sex_morb rn; var ravens relyear; output out = mean_rav; run; data means2; set mean_rav; where _STAT_ = "MEAN"; run; proc gplot data = means2; plot ravens*relyear = sex_morb / nolegend name = 'f79_b'; run; quit; * (b); goptions reset = all; symbol1 value=none color = black interpol=join r=6; proc sort data = cogp2; by sex_morb rn; run; proc means data = cogp2; by sex_morb rn; var pred relyear; output out = mean_rav; run; data means2; set mean_rav; where _STAT_ = "MEAN"; run; proc gplot data = means2; plot pred*relyear = sex_morb / nolegend name = 'f79_a'; run; quit; proc greplay igout = work.gseg tc=sashelp.templt template=h2 nofs; treplay 1:f79_a 2:f79_b; run; quit;
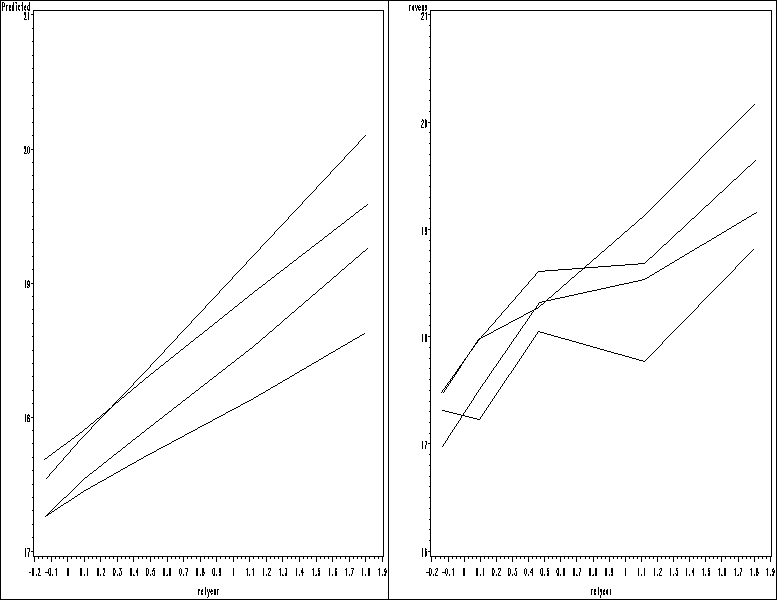
Table 7.12, page 225.
data bsi;
set bsitotal;
knot18 = (true_month - 18)*(true_month >= 18);
knot36 = (true_month - 36)*(true_month >= 36);
spring = (season = "spring (3-6)");
summer = (season = "summer (7-10)");
l2bsi_gsi = log2(bsi_gsi + 1/53);
run;
proc mixed data=bsi noclprint noitprint covtest method = reml;
class pid parent rounded3_true_month gender ;
model l2bsi_gsi = true_month knot18 knot36 spring summer gender / solution notest;
repeated rounded3_true_month /subject=pid(parent) type=arma(1,1);
random intercept / subject=parent;
estimate 'slope before 18' true_month 1;
estimate 'slope 18-36' true_month 1 knot18 1;
estimate 'slope after 36' true_month 1 knot18 1 knot36 1;
estimate 'spring - summer' spring 1 summer -1;
run ;
The Mixed Procedure
Model Information
Data Set WORK.BSI
Dependent Variable l2bsi_gsi
Covariance Structures Variance Components,
Autoregressive
Moving Average
Subject Effects parent, pid(parent)
Estimation Method REML
Residual Variance Method Profile
Fixed Effects SE Method Model-Based
Degrees of Freedom Method Containment
Dimensions
Covariance Parameters 4
Columns in X 8
Columns in Z Per Subject 1
Subjects 280
Max Obs Per Subject 70
Number of Observations
Number of Observations Read 4857
Number of Observations Used 4857
Number of Observations Not Used 0
Covariance Parameter Estimates
Standard Z
Cov Parm Subject Estimate Error Value Pr Z
Intercept parent 0.4541 0.1586 2.86 0.0021
Rho pid(parent) 0.9516 0.006524 145.88 <.0001
Gamma pid(parent) 0.5846 0.02232 26.19 <.0001
Residual 3.3062 0.1711 19.32 <.0001
Fit Statistics
-2 Res Log Likelihood 17551.1
AIC (smaller is better) 17559.1
AICC (smaller is better) 17559.1
BIC (smaller is better) 17573.7
Solution for Fixed Effects
Standard
Effect gender Estimate Error DF t Value Pr > |t|
Intercept -1.8566 0.1204 279 -15.42 <.0001
true_month -0.06238 0.004810 4571 -12.97 <.0001
knot18 0.08056 0.008174 4571 9.86 <.0001
knot36 -0.02015 0.006589 4571 -3.06 0.0022
spring 0.1608 0.04415 4571 3.64 0.0003
summer -0.01344 0.04498 4571 -0.30 0.7652
gender female 0.6524 0.1337 4571 4.88 <.0001
gender male 0 . . . .
Estimates
Standard
Label Estimate Error DF t Value Pr > |t|
slope before 18 -0.06238 0.004810 4571 -12.97 <.0001
slope 18-36 0.01818 0.004849 4571 3.75 0.0002
slope after 36 -0.00197 0.002899 4571 -0.68 0.4962
spring - summer 0.1742 0.04482 4571 3.89 0.0001
Table 7.13, page 227.
data bmice_knot;
set bigmice;
cont_day = day;
day2 = day**2;
day3 = day**3;
knot3_5 = (day-3.5)**3*(day>=3.5);
knot8_5 = (day-8.5)**3*(day>=8.5);
knot13_5 = (day-13.5)**3*(day>=13.5);
run;
proc mixed data = bmice_knot method = ml noitprint noclprint;
class id day;
model weight = cont_day day2 day3 knot3_5 knot8_5 knot13_5
/solution notest;
repeated day / subject = id type = arh(1);
run;
The Mixed Procedure
Model Information
Data Set WORK.BMICE_KNOT
Dependent Variable weight
Covariance Structure Heterogeneous
Autoregressive
Subject Effect id
Estimation Method ML
Residual Variance Method None
Fixed Effects SE Method Model-Based
Degrees of Freedom Method Between-Within
Dimensions
Covariance Parameters 22
Columns in X 7
Columns in Z 0
Subjects 35
Max Obs Per Subject 21
Number of Observations
Number of Observations Read 735
Number of Observations Used 273
Number of Observations Not Used 462
Covariance Parameter Estimates
Cov Parm Subject Estimate
Var(1) id 228.20
Var(2) id 333.26
Var(3) id 2297.80
Var(4) id 1723.93
Var(5) id 2141.12
Var(6) id 2485.15
Var(7) id 3827.81
Var(8) id 3556.06
Var(9) id 2915.58
Var(10) id 7403.05
Var(11) id 6433.77
Var(12) id 6046.23
Var(13) id 5569.73
Var(14) id 6010.33
Var(15) id 7936.64
Var(16) id 6861.19
Var(17) id 9133.41
Var(18) id 7948.99
Var(19) id 7422.95
Var(20) id 9994.02
Var(21) id 6924.31
ARH(1) id 0.9369
Fit Statistics
-2 Log Likelihood 2716.7
AIC (smaller is better) 2774.7
AICC (smaller is better) 2781.9
BIC (smaller is better) 2819.8
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
21 481.61 <.0001
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 148.78 2.7697 34 53.72 <.0001
cont_day 5.9927 4.2493 232 1.41 0.1598
day2 13.6207 2.1150 232 6.44 <.0001
day3 -1.2283 0.2693 232 -4.56 <.0001
knot3_5 1.0482 0.3501 232 2.99 0.0031
knot8_5 0.1476 0.1784 232 0.83 0.4089
knot13_5 0.3786 0.2276 232 1.66 0.0975
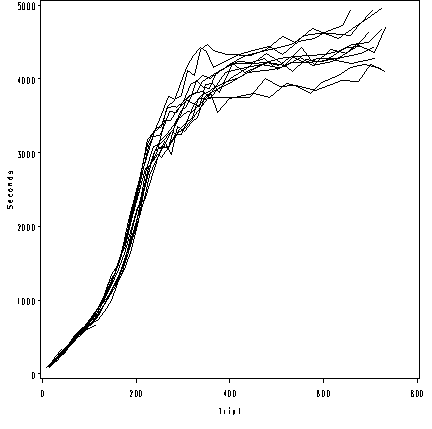
Figure 7.11(a), page 229. (b-d) omitted because SAS does not allow random effects with spline models.
goptions reset = all; symbol1 value=none color = black interpol=join r=20; axis1 order =(0 to 800 by 200) label=(a=0 'Trial') minor=none; axis2 order =(0 to 5000 by 1000) label = (a=90 'Seconds') minor=none ; proc gplot data = small_wallaby; where animal le 76 ; plot tail*agedays =animal /haxis=axis1 vaxis = axis2 nolegend; run; quit;