Page 242 Table 11.1 Means and standard deviations for nondepressed and depressed adults in Los Angeles County
data depress; set "c:\pma5\depress"; run; proc sort data = depress out=depress; by cases; run; proc means data = depress mean std; var sex age educat income health beddays acuteill chronill; by cases; run; CASES=0 The MEANS Procedure Variable Mean Std Dev ---------------------------------------- SEX 1.5860656 0.4935494 AGE 45.2418033 18.1464928 EDUCAT 3.5450820 1.3310228 INCOME 21.6762295 15.9754727 HEALTH 1.7131148 0.7958690 BEDDAYS 0.1721311 0.3782703 ACUTEILL 0.2786885 0.4492755 CHRONILL 0.4836066 0.5007584 ---------------------------------------- CASES=1 Variable Mean Std Dev ---------------------------------------- SEX 1.8000000 0.4040610 AGE 40.3800000 17.4003167 EDUCAT 3.1600000 1.1668902 INCOME 15.2000000 9.8374545 HEALTH 2.0600000 0.9775020 BEDDAYS 0.4200000 0.4985694 ACUTEILL 0.3800000 0.4903144 CHRONILL 0.6200000 0.4903144 ----------------------------------------
Page 244 Figure 11.2 Distribution of income for depressed and nondepressed individuals showing effects of a dividing point at an income of $18440.
NOTE: We were unable to reproduce this graph.
Page 245 Table 11.2 Classification of individuals as depressed or not depressed on the basis of income alone.
proc discrim data = depress;
class cases;
var income;
run;
(some output omitted)
Number of Observations and Percent Classified into CASES
From
CASES 0 1 Total
0 121 123 244
49.59 50.41 100.00
1 19 31 50
38.00 62.00 100.00
Total 140 154 294
47.62 52.38 100.00
Page 248 Figure 11.5 Classification of individuals as depressed or not depressed on the basis of income and age.
NOTE: The line can be added using an annotated data set.
goptions reset = all;
goptions cells;
axis1 order=(0 to 65 by 5) label=('Income') label=(a=90 r = 0);
axis2 order=(15 to 90 by 5) label=('Age');
symbol1 v=triangle height=1 cells c=blue;
symbol2 v=circle height=1 cells c=red;
proc gplot data=depress ;
plot income*age = cases /vaxis = axis1 haxis = axis2;
run;
quit;
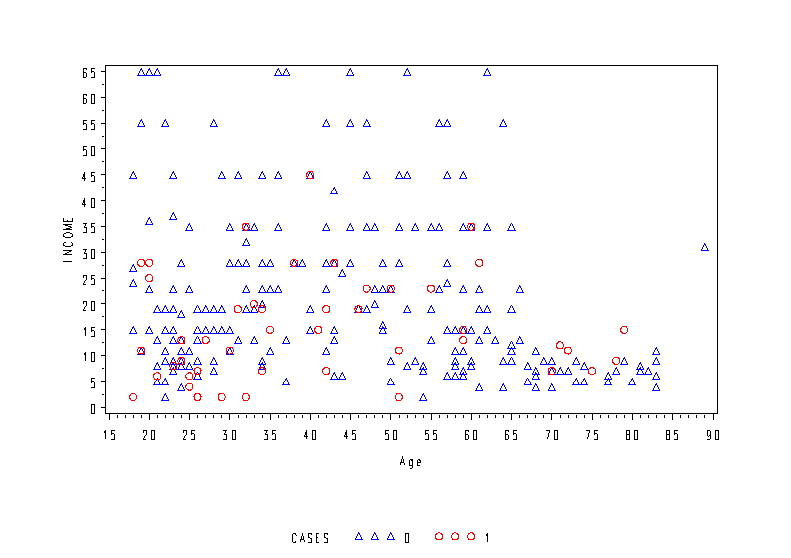
Page 249 Table 11.3 Classification of individuals as depressed or not depressed on the basis of income and age
proc discrim data = depress;
class cases;
var income age;
run;
(some output omitted)
Number of Observations and Percent Classified into CASES
From
CASES 0 1 Total
0 154 90 244
63.11 36.89 100.00
1 20 30 50
40.00 60.00 100.00
Total 174 120 294
59.18 40.82 100.00
Page 253 Table 11.4 Classification function and discriminant coefficients for age and income
NOTE: We do not know why the constant is incorrect.
NOTE: We do not know how to get the discriminant functions.
proc discrim data = depress; class cases; var age income; run; (some output omitted) Linear Discriminant Function for CASES Variable 0 1 Constant -5.17094 -3.65520 AGE 0.16342 0.14249 INCOME 0.13603 0.10242
Page 254 Covariances at the top of the page
proc corr data = depress cov;
var age income;
run;
The CORR Procedure
2 Variables: AGE INCOME
Covariance Matrix, DF = 293
AGE INCOME
AGE 327.0831882 -53.0072671
INCOME -53.0072671 233.7878967
(some output omitted)
Page 261 top of the page
NOTE: We have omitted most of the output from the proc discrim. The F test is produced by the manova option on the proc discrim statement.
proc discrim data = depress manova;
class cases;
var income age;
run;
(some output omitted)
The DISCRIM Procedure
Multivariate Statistics and Exact F Statistics
S=1 M=0 N=144.5
Statistic Value F Value Num DF Den DF Pr > F
Wilks' Lambda 0.95657959 6.60 2 291 0.0016
Pillai's Trace 0.04342041 6.60 2 291 0.0016
Hotelling-Lawley Trace 0.04539132 6.60 2 291 0.0016
Roy's Greatest Root 0.04539132 6.60 2 291 0.0016
Page 261 bottom of the page
NOTE: This F test is comparing two models. Hence we need to run proc discrim twice to get the numbers that we need. We have included only the relevant output below.
proc discrim data = depress;
class cases;
var income;
run;
The DISCRIM Procedure
Observations 294 DF Total 293
Variables 1 DF Within Classes 292
Classes 2 DF Between Classes 1
Class Level Information
Variable Prior
cases Name Frequency Weight Proportion Probability
0 _0 244 244.0000 0.829932 0.500000
1 _1 50 50.0000 0.170068 0.500000
Generalized Squared Distance to cases
From
cases 0 1
0 0 0.18345
1 0.18345 0
proc discrim data = depress;
class cases;
var income age;
run;
The DISCRIM Procedure
Observations 294 DF Total 293
Variables 2 DF Within Classes 292
Classes 2 DF Between Classes 1
Class Level Information
Variable Prior
cases Name Frequency Weight Proportion Probability
0 _0 244 244.0000 0.829932 0.500000
1 _1 50 50.0000 0.170068 0.500000
Generalized Squared Distance to cases
From
cases 0 1
0 0 0.31941
1 0.31941 0
