Version info: Code for this page was tested in SAS 9.3.
For this chapter, you will need to use the syntax provided in Appendix A to access the School and Mice datasets.
Figure 18.2, page 466 is not reproduced.
Table 18.2, page 468 Estimated coefficients from three naive linear regression models ignoring the hierarchical structure of the school data. Note that for Model 3, we believe there is a typo where the coefficient for “Three hours” was copied for “Four or more hours”.
PROC SORT data = School;
by descending newSCHTYPE descending newHW;
RUN;
/* Table 18.2 */
PROC GLM data = School order = data;
class newSCHTYPE;
model MATH = newSCHTYPE / solution;
RUN;
The GLM Procedure
Dependent Variable: MATH
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 1 7517.11179 7517.11179 74.89 <.0001 Error 517 51890.93446 100.36931 Corrected Total 518 59408.04624 R-Square Coeff Var Root MSE MATH Mean 0.126534 19.36960 10.01845 51.72254 Source DF Type I SS Mean Square F Value Pr > F
newSCHTYPE 1 7517.111786 7517.111786 74.89 <.0001 Source DF Type III SS Mean Square F Value Pr > F
newSCHTYPE 1 7517.111786 7517.111786 74.89 <.0001 Standard Parameter Estimate Error t Value Pr > |t|
Intercept 56.49009901 B 0.70489558 80.14 <.0001
newSCHTYPE 1 -7.80555642 B 0.90194247 -8.65 <.0001
newSCHTYPE 0 0.00000000 B . . .
NOTE: The X'X matrix has been found to be singular, and a generalized inverse was used to solve
the normal equations. Terms whose estimates are followed by the letter 'B' are not
uniquely estimable.
PROC GLM data = School order = data;
class newSCHTYPE;
model MATH = newSCHTYPE SES / solution;
RUN;
The GLM Procedure
Dependent Variable: MATH
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 2 14923.96488 7461.98244 86.56 <.0001 Error 516 44484.08136 86.20946 Corrected Total 518 59408.04624 R-Square Coeff Var Root MSE MATH Mean 0.251211 17.95137 9.284905 51.72254 Source DF Type I SS Mean Square F Value Pr > F
newSCHTYPE 1 7517.111786 7517.111786 87.20 <.0001
SES 1 7406.853097 7406.853097 85.92 <.0001 Source DF Type III SS Mean Square F Value Pr > F
newSCHTYPE 1 621.850871 621.850871 7.21 0.0075
SES 1 7406.853097 7406.853097 85.92 <.0001 Standard Parameter Estimate Error t Value Pr > |t|
Intercept 53.37221655 B 0.73479649 72.64 <.0001
newSCHTYPE 1 -2.69017405 B 1.00164705 -2.69 0.0075
newSCHTYPE 0 0.00000000 B . . .
SES 5.14426413 0.55498834 9.27 <.0001
NOTE: The X'X matrix has been found to be singular, and a generalized inverse was used to solve
the normal equations. Terms whose estimates are followed by the letter 'B' are not
uniquely estimable.
PROC GLM data = School order = data;
class newSCHTYPE newHW;
model MATH = newSCHTYPE SES newHW / solution;
RUN;
The GLM Procedure
Dependent Variable: MATH
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 7 20787.19803 2969.59972 39.29 <.0001 Error 511 38620.84821 75.57896 Corrected Total 518 59408.04624 R-Square Coeff Var Root MSE MATH Mean 0.349905 16.80818 8.693616 51.72254 Source DF Type I SS Mean Square F Value Pr > F
newSCHTYPE 1 7517.111786 7517.111786 99.46 <.0001
SES 1 7406.853097 7406.853097 98.00 <.0001
newHW 5 5863.233151 1172.646630 15.52 <.0001 Source DF Type III SS Mean Square F Value Pr > F
newSCHTYPE 1 215.042228 215.042228 2.85 0.0923
SES 1 4888.876929 4888.876929 64.69 <.0001
newHW 5 5863.233151 1172.646630 15.52 <.0001 Standard Parameter Estimate Error t Value Pr > |t|
Intercept 51.37485359 B 1.50805261 34.07 <.0001
newSCHTYPE 1 -1.60459840 B 0.95127248 -1.69 0.0923
newSCHTYPE 0 0.00000000 B . . .
SES 4.27563995 0.53161476 8.04 <.0001
newHW 5 8.07390470 B 1.91180028 4.22 <.0001
newHW 4 7.56010333 B 1.88968358 4.00 <.0001
newHW 3 5.20851187 B 1.85282204 2.81 0.0051
newHW 2 0.22640909 B 1.57858349 0.14 0.8860
newHW 1 -1.39021887 B 1.46388306 -0.95 0.3427
newHW 0 0.00000000 B . . .
NOTE: The X'X matrix has been found to be singular, and a generalized inverse was used to solve
the normal equations. Terms whose estimates are followed by the letter 'B' are not
uniquely estimable.
Table 18.3, page 472 Estimated coefficients from three random slope regression models accounting for the hierarchical structure of the school data.
/* Table 18.3 */
PROC MIXED data = School order = data noclprint;
class newSCHTYPE SCHOOL;
model MATH = newSCHTYPE / solution;
random Int / type = un sub=SCHOOL;
RUN;
The Mixed Procedure
Model Information
Data Set WORK.SCHOOL
Dependent Variable MATH
Covariance Structure Unstructured
Subject Effect SCHOOL
Estimation Method REML
Residual Variance Method Profile
Fixed Effects SE Method Model-Based
Degrees of Freedom Method Containment
Dimensions
Covariance Parameters 2
Columns in X 3
Columns in Z Per Subject 1
Subjects 23
Max Obs Per Subject 67
Number of Observations
Number of Observations Read 519
Number of Observations Used 519
Number of Observations Not Used 0
Iteration History
Iteration Evaluations -2 Res Log Like Criterion
0 1 3861.02842646
1 3 3789.18082462 0.00034325
2 1 3788.60625480 0.00004068
3 1 3788.54373285 0.00000078
4 1 3788.54261121 0.00000000
Convergence criteria met.
Covariance Parameter Estimates
Cov Parm Subject Estimate
UN(1,1) SCHOOL 19.1533
Residual 81.2337
Fit Statistics
-2 Res Log Likelihood 3788.5
AIC (smaller is better) 3792.5
AICC (smaller is better) 3792.6
BIC (smaller is better) 3794.8
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
1 72.49 <.0001 Solution for Fixed Effects new Standard Effect SCHTYPE Estimate Error DF t Value Pr > |t|
Intercept 54.6684 1.7402 21 31.41 <.0001 newSCHTYPE 1 -5.9060 2.1369 496 -2.76 0.0059 newSCHTYPE 0 0 . . . . Type 3 Tests of Fixed Effects Num Den Effect DF DF F Value Pr > F
newSCHTYPE 1 496 7.64 0.0059
PROC MIXED data = School order = data noclprint;
class newSCHTYPE SCHOOL;
model MATH = newSCHTYPE SES / solution;
random Int / type = un sub=SCHOOL;
RUN;
[some output ommitted]
Covariance Parameter Estimates
Cov Parm Subject Estimate
UN(1,1) SCHOOL 12.2516
Residual 75.2895
Fit Statistics
-2 Res Log Likelihood 3741.4
AIC (smaller is better) 3745.4
AICC (smaller is better) 3745.4
BIC (smaller is better) 3747.6
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
1 39.39 <.0001 Solution for Fixed Effects new Standard Effect SCHTYPE Estimate Error DF t Value Pr > |t|
Intercept 52.8099 1.4733 21 35.85 <.0001
newSCHTYPE 1 -2.4527 1.8448 495 -1.33 0.1843
newSCHTYPE 0 0 . . . .
SES 4.1319 0.5869 495 7.04 <.0001 Type 3 Tests of Fixed Effects Num Den Effect DF DF F Value Pr > F
newSCHTYPE 1 495 1.77 0.1843
SES 1 495 49.56 <.0001
PROC MIXED data = School order = data noclprint;
class newSCHTYPE newHW SCHOOL;
model MATH = newSCHTYPE SES newHW / solution;
random Int / type = un sub=SCHOOL;
RUN;
[some output ommitted]
Covariance Parameter Estimates
Cov Parm Subject Estimate
UN(1,1) SCHOOL 11.8628
Residual 65.8440
Fit Statistics
-2 Res Log Likelihood 3657.4
AIC (smaller is better) 3661.4
AICC (smaller is better) 3661.4
BIC (smaller is better) 3663.7
Null Model Likelihood Ratio Test
DF Chi-Square Pr > ChiSq
1 38.62 <.0001 Solution for Fixed Effects new new Standard Effect SCHTYPE HW Estimate Error DF t Value Pr > |t|
Intercept 50.9881 1.9106 21 26.69 <.0001
newSCHTYPE 1 -1.6503 1.7931 490 -0.92 0.3578
newSCHTYPE 0 0 . . . .
SES 3.4652 0.5578 490 6.21 <.0001
newHW 5 7.7219 1.8686 490 4.13 <.0001
newHW 4 7.6464 1.8339 490 4.17 <.0001 newHW 3 5.3106 1.8002 490 2.95 0.0033 newHW 2 0.7257 1.5419 490 0.47 0.6381 newHW 1 -1.2868 1.4251 490 -0.90 0.3670 newHW 0 0 . . . . Type 3 Tests of Fixed Effects Num Den Effect DF DF F Value Pr > F
newSCHTYPE 1 490 0.85 0.3578
SES 1 490 38.60 <.0001
newHW 5 490 15.45 <.0001
Figure 18.3 is not reproduced.
Table 18.4, page 480 is not reproduced. To create it, you can simply run models for all pairwise combination of variables.
Figure 18.4, page 483 Weight over time for 14 Mice.
/*Figure 18.4 page 483 */ symbol1 value = circle color = black interpol = join repeat = 14; PROC GPLOT data = Mice; plot WEIGHT * DAY = ID / nolegend; RUN; QUIT;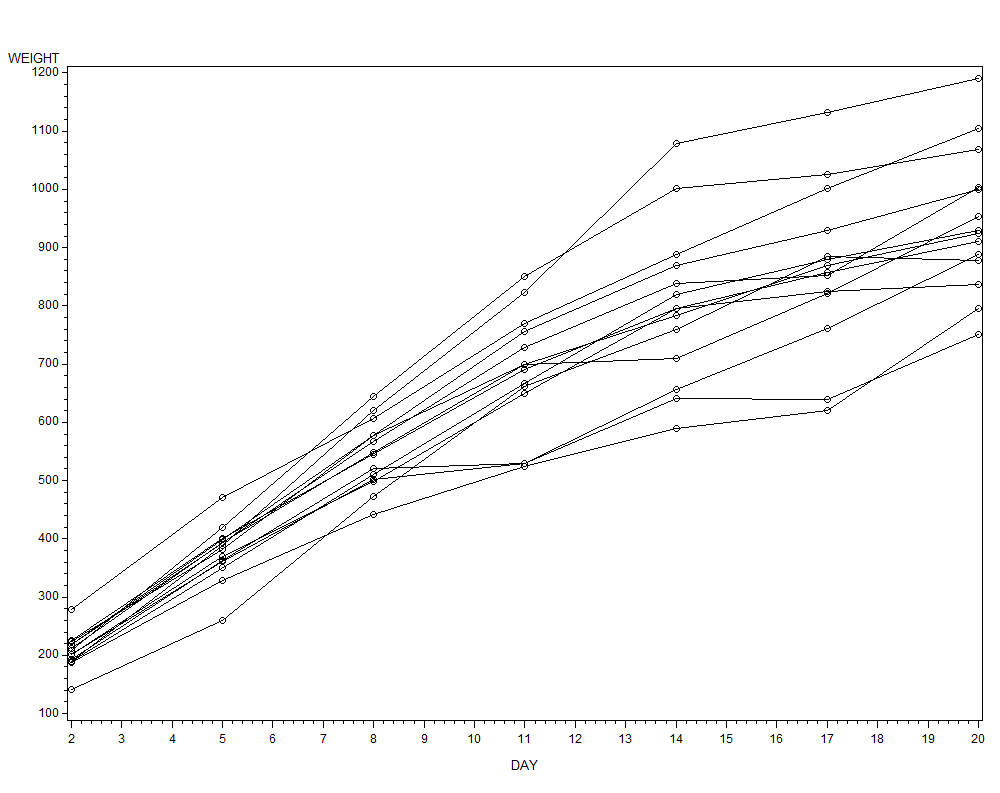
Table 18.5, page 485Estimates for random intercept and random slope models with different correlation structures. Note that these are complex random effects models to be fitting on only 14 mice. The parameter estimates vary between packages, with some reporting Errors or warnings in the optimization.
DATA Mice;
set Mice;
cDAY = DAY;
RUN;
PROC SORT data = Mice;
by cDAY;
RUN;
/* Table 18.5, page 485*/
PROC MIXED data = Mice METHOD=ML noclprint;
class ID cDay;
model WEIGHT = DAY / solution;
random int DAY / subject = ID;
repeated cDAY / subject = ID type = AR(1);
RUN;
The Mixed Procedure
Model Information
Data Set WORK.MICE
Dependent Variable WEIGHT
Covariance Structures Variance Components,
Autoregressive
Subject Effects ID, ID
Estimation Method ML
Residual Variance Method Profile
Fixed Effects SE Method Model-Based
Degrees of Freedom Method Containment
Dimensions
Covariance Parameters 4
Columns in X 2
Columns in Z Per Subject 2
Subjects 14
Max Obs Per Subject 7
Number of Observations
Number of Observations Read 98
Number of Observations Used 98
Number of Observations Not Used 0
Iteration History
Iteration Evaluations -2 Log Like Criterion
0 1 1189.14416371
1 3 1084.16542429 0.00090715
2 2 1083.77544184 0.00005750
3 1 1083.74783386 0.00000073
4 1 1083.74749894 0.00000000
Convergence criteria met.
Covariance Parameter Estimates
Cov Parm Subject Estimate
Intercept ID 0
DAY ID 25.7119
AR(1) ID 0.7166
Residual 5931.47
Fit Statistics
-2 Log Likelihood 1083.7
AIC (smaller is better) 1093.7
AICC (smaller is better) 1094.4
BIC (smaller is better) 1096.9
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 156.82 22.0092 13 7.13 <.0001
DAY 41.0553 2.0202 13 20.32 <.0001 Type 3 Tests of Fixed Effects Num Den Effect DF DF F Value Pr > F
DAY 1 13 413.02 <.0001
PROC MIXED data = Mice METHOD=ML noclprint;
class ID cDay;
model WEIGHT = DAY / solution;
random int DAY / subject = ID;
repeated cDAY / subject = ID type = cs;
RUN;
Covariance Parameter Estimates
Cov Parm Subject Estimate
Intercept ID 0
DAY ID 50.4134
CS ID -533.47
Residual 3734.32
Fit Statistics
-2 Log Likelihood 1118.3
AIC (smaller is better) 1128.3
AICC (smaller is better) 1129.0
BIC (smaller is better) 1131.5
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 180.41 11.3171 13 15.94 <.0001
DAY 41.0544 2.1586 13 19.02 <.0001 Type 3 Tests of Fixed Effects Num Den Effect DF DF F Value Pr > F
DAY 1 13 361.73 <.0001
