Section 5.2
Estimating the Survival Function for Left, Double, and Interval Censoring
Example 5.1 illustrating Turnbull’s algorithm. We therefore create Table 5.1, Table 5.2 and Table 5.3 all through data steps and proc sql to show the steps.
data table5_1;
input age num_lcen num_event num_rcen;
cards;
0 0 0 0
10 0 4 0
11 0 12 0
12 0 19 2
13 1 24 15
14 2 20 24
15 3 13 18
16 2 3 14
17 3 1 6
18 1 0 0
19 0 4 0
;
run;
proc sql noprint;
select sum(num_event)+ sum(num_rcen) into :total
from table5_1;
quit;
data table5_1a;
set table5_1;
id = _n_;
elag = lag(num_event);
rlag = lag(num_rcen);
retain y &total survival 1;
if _n_ >= 2 then y = y - rlag - elag;
survival = survival*(1-num_event/y);
drop elag rlag;
run;
proc print data=table5_1a noobs;
var id num_lcen num_event num_rcen y survival;
run;
num_
id num_lcen event num_rcen y survival
1 0 0 0 179 1.00000
2 0 4 0 179 0.97765
3 0 12 0 175 0.91061
4 0 19 2 163 0.80447
5 1 24 15 142 0.66850
6 2 20 24 103 0.53870
7 3 13 18 59 0.42000
8 2 3 14 28 0.37500
9 3 1 6 11 0.34091
10 1 0 0 4 0.34091
11 0 4 0 4 0.0000
Table 5.2, step 1 of Turnbull’s algorithm.
data table5_2;
set table5_1a;
keep survival;
run;
proc sort data = table5_2;
by descending survival ;
run;
proc transpose data=table5_2 out=long52 (drop = _name_);
var survival;
run;
proc sql;
create table table5_2b as
select *
from table5_1a , long52;
quit;
data table5_2c;
set table5_2b nobs=last;
slag = lag(survival);
array s(11) col1-col11;
array p(11);
do i = 2 to 10;
p(i) = (slag - survival)/(1 - s(i+1));
end;
if _n_ = last then
do i = 2 to 10;
p(i) = 0;
end;
run;
proc print data = table5_2c ;
var p4-p9;
where p2 ne . ;
run;
Obs p4 p5 p6 p7 p8 p9 2 0.06741 0.04844 0.03853 0.03575 0.03390 0.03390 3 0.20223 0.14533 0.11558 0.10726 0.10171 0.10171 4 0.32020 0.23010 0.18301 0.16983 0.16105 0.16105 5 0.41016 0.29474 0.23443 0.21755 0.20629 0.20629 6 0.39158 0.28139 0.22380 0.20769 0.19695 0.19695 7 0.35806 0.25731 0.20465 0.18991 0.18009 0.18009 8 0.13575 0.09755 0.07759 0.07200 0.06828 0.06828 9 0.10284 0.07390 0.05878 0.05455 0.05172 0.05172 10 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 11 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000
Table 5.3, the first step of the Self-Consistency Algorithm.
data table5_3;
set table5_2c;
array p(6) p4-p9;
if _n_ >=6 then
do i = 1 to _n_ - 5;
p(i) = 0;
end;
if _n_ = 1 then dhat = 0;
else dhat = num_event + p4 + 2*p5 + 3*p6 + 2*p7 + 3*p8 + p9;
run;
proc sql noprint;
select sum(dhat) + sum(num_rcen) into :totaly
from table5_3;
quit;
data table5_3a;
set table5_3;
dlag = lag(dhat);
rlag = lag(num_rcen);
retain yhat &totaly survival1 1;
if _n_>=2 then yhat = yhat - dlag - rlag;
survival1 = survival1*abs((1-dhat/yhat));
run;
proc print data=table5_3a noobs;
var id age dhat num_rcen yhat survival1;
run;
id age dhat num_rcen yhat survival1
1 0 0.0000 0 191.000 1.00000
2 10 4.4870 0 191.000 0.97651
3 11 13.4610 0 186.513 0.90603
4 12 21.3133 2 173.052 0.79444
5 13 26.9632 15 149.739 0.65139
6 14 22.4374 24 107.775 0.51578
7 15 14.7141 18 61.338 0.39205
8 16 3.4171 14 28.624 0.34525
9 17 1.2069 6 11.207 0.30807
10 18 0.0000 0 4.000 0.30807
11 19 4.0000 0 4.000 0.00000
Example 5.2 on estimation procedure for interval-censored data. It uses the data described in section 1.18. SAS currently doesn’t have a standard procedure on nonparametric survival analysis for interval-censored data. But it has a macro %ice that performs the analysis. Macro %ice makes use of a utility program called xmacro.sas. Program ice.sas is located at Both of the programs can be found from SAS. Here is a link to %ice and xmacro.sas. You need to download both programs for Example 5.2.
Section 5.3
Estimation of the Survival Function for Right-Truncated Data
This section uses the data set described in section 1.19. We created a SAS data step for it.
Example 6.3, Table 6.3 and Figure 6.8. The first part of the program creates the hazard rate based on the Iowa life table. The macro does the computation for table 6.3 including the confidence intervals. We notice that the output produced below does not match with Table 6.3 completely. The data for table 6.3 is then used for Figure 6.8.
proc sort data = iowa_60_mortality;
by male;
run;
data table6_2;
set iowa_60_mortality;
by male;
ls = lag(survival);
if ~first.male then do;
hr = log(ls) - log(survival); end;
drop survival;
if hr ~=.;
run;
%macro rel_mortality(data, age, time, death, outdata);
proc sql noprint;
select count( distinct &time) into :max_num
from &data
where &death = 1;
quit;
proc sql noprint;
select count(&time) into :dpoint separated by ' '
from &data
where &death = 1
group by &time;
quit;
proc sql noprint;
select distinct &time into :tpoint separated by ' '
from &data
where &death = 1;
quit;
%do k = 1 %to &max_num;
%let p = %scan(&tpoint, &k);
proc sql noprint;
select sum(y.hr) into :q&k
from &data as x, table6_2 as y
where 1-x.female = y.male and x.age + &p + 1 = y.age and x.time >= &p ;
quit;
%end;
data &outdata;
b = 0;
v = 0;
%do i = 1 %to &max_num;
t = %scan(&tpoint, &i);
d = %scan(&dpoint, &i);
q = &&q&i;
b = b + d/q;
v = v + d/q**2;
s = sqrt(v);
lc = b/exp(1.96*s/b);/*log-transformed confidence interval*/
uc = b*exp(1.96*s/b);
output;
%end;
run;
proc print data= &outdata noobs;
var t d q b v s lc uc;
run;
%mend rel_mortality;
%rel_mortality(sec1_15, age, time, death, temp)
t d q b v s lc uc
1 2 0.05932 33.718 568.44 23.8420 8.4325 134.822
2 1 0.04964 53.861 974.20 31.2122 17.2982 167.707
11 1 0.08524 65.593 1111.84 33.3443 24.2183 177.654
14 1 0.10278 75.323 1206.51 34.7349 30.5066 185.979
22 2 0.18238 86.289 1266.64 35.5899 38.4478 193.660
24 1 0.21559 90.928 1288.15 35.8909 41.9472 197.100
25 1 0.17002 96.809 1322.75 36.3696 46.3583 202.164
26 1 0.19441 101.953 1349.20 36.7315 50.3179 206.574
28 1 0.18434 107.377 1378.63 37.1299 54.5220 211.473
32 1 0.18562 112.765 1407.66 37.5187 58.7436 216.465
35 1 0.16755 118.733 1443.28 37.9905 63.4180 222.296
40 1 0.04902 139.135 1859.50 43.1219 75.7912 255.419
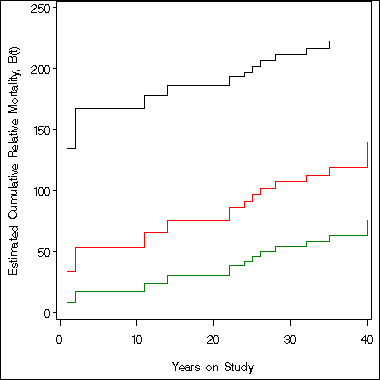
symbol i = stepjl;
axis1 order = (0 to 250 by 50) label=(a=90 'Estimated Cumulative Relative Mortality, B(t)')
minor = none;
axis2 order = (0 to 40 by 10) minor = none label=('Years on Study');
proc gplot data= temp;
plot uc*t b*t lc*t/overlay vaxis = axis1 haxis = axis2;
run;
quit;
Example 6.3 continued on page 169. Table 6.4, Figure 6.9 and Figure 6.10. The proc sql step and data steps below prepares us to create Table 6.4. The macro program generates Table 6.4.
proc sql;
create table table6_4 as
select time, sum(death) as d, sum(death=0) as censor
from sec1_15
group by time;
quit;
data table6_4a;
do time = 1 to 40;
output; end;
run;
data table6_4b;
merge table6_4 table6_4a ;
by time;
if d = . then d = 0;
if censor = . then censor = 0;
retain y 26;
ld = lag(d);
lc = lag(censor);
if _n_>1 then y = y-ld - lc;
drop ld lc;
run;
%macro theta(data, time, max, outdata);
%do k = 1 %to &max;
proc sql noprint;
select sum(y.hr) into :q&k
from &data as x, table6_2 as y
where 1-x.female = y.male and x.age + &k = y.age and x.time > &k - 1 ;
quit;
%end;
data &outdata;
set table6_4b;
retain theta 0;
retain p var_a 0;
retain h 0;
retain s1 1;
q = symget('q'||left(_n_));
theta = theta + q/y;
p = p + d/y;
h = h + d/y;
s1 = s1*(1-d/y);
var_a = var_a + d/y**2;
a = p - theta;
sda = sqrt(var_a);
survival = exp(-theta);
sc = s1/survival;
drop q p censor;
run;
proc print data = temp noobs;
var time d y h theta a sda s1 survival sc;
run;
%mend;
%theta(sec1_15, time, 40, temp)
time d y h theta a sda s1 survival sc
1 2 26 0.07692 0.00213 0.07479 0.05439 0.92308 0.99787 0.92505
2 1 24 0.11859 0.00406 0.11453 0.06852 0.88462 0.99595 0.88822
3 0 23 0.11859 0.00594 0.11265 0.06852 0.88462 0.99408 0.88988
4 0 23 0.11859 0.00794 0.11065 0.06852 0.88462 0.99209 0.89167
5 0 23 0.11859 0.01008 0.10851 0.06852 0.88462 0.98997 0.89358
6 0 23 0.11859 0.01237 0.10622 0.06852 0.88462 0.98771 0.89563
7 0 23 0.11859 0.01483 0.10376 0.06852 0.88462 0.98528 0.89783
8 0 23 0.11859 0.01747 0.10112 0.06852 0.88462 0.98269 0.90020
9 0 23 0.11859 0.02032 0.09827 0.06852 0.88462 0.97989 0.90277
10 0 23 0.11859 0.02341 0.09518 0.06852 0.88462 0.97686 0.90557
11 1 23 0.16207 0.02679 0.13528 0.08115 0.84615 0.97357 0.86913
12 0 22 0.16207 0.03029 0.13178 0.08115 0.84615 0.97016 0.87218
13 0 22 0.16207 0.03414 0.12793 0.08115 0.84615 0.96643 0.87554
14 1 22 0.20752 0.03838 0.16914 0.09301 0.80769 0.96235 0.83929
15 0 21 0.20752 0.04279 0.16473 0.09301 0.80769 0.95811 0.84300
16 0 21 0.20752 0.04811 0.15941 0.09301 0.80769 0.95303 0.84750
17 0 21 0.20752 0.05297 0.15455 0.09301 0.80769 0.94841 0.85163
18 0 21 0.20752 0.05882 0.14871 0.09301 0.80769 0.94288 0.85662
19 0 21 0.20752 0.06522 0.14230 0.09301 0.80769 0.93686 0.86213
20 0 21 0.20752 0.07222 0.13530 0.09301 0.80769 0.93032 0.86818
21 0 21 0.20752 0.08035 0.12717 0.09301 0.80769 0.92280 0.87527
22 2 21 0.30276 0.08872 0.21405 0.11483 0.73077 0.91511 0.79856
23 0 19 0.30276 0.09674 0.20603 0.11483 0.73077 0.90780 0.80499
24 1 19 0.35539 0.10611 0.24928 0.12632 0.69231 0.89932 0.76981
25 1 18 0.41095 0.11683 0.29411 0.13800 0.65385 0.88973 0.73488
26 1 17 0.46977 0.12554 0.34423 0.15001 0.61538 0.88202 0.69770
27 0 16 0.46977 0.13628 0.33349 0.15001 0.61538 0.87260 0.70524
28 1 16 0.53227 0.14737 0.38490 0.16251 0.57692 0.86297 0.66853
29 0 15 0.53227 0.15924 0.37303 0.16251 0.57692 0.85279 0.67651
30 0 15 0.53227 0.17294 0.35933 0.16251 0.57692 0.84119 0.68584
31 0 13 0.53227 0.18722 0.34505 0.16251 0.57692 0.82926 0.69571
32 1 11 0.62318 0.20356 0.41962 0.18621 0.52448 0.81582 0.64288
33 0 10 0.62318 0.22147 0.40171 0.18621 0.52448 0.80134 0.65450
34 0 8 0.62318 0.24193 0.38125 0.18621 0.52448 0.78511 0.66803
35 1 7 0.76604 0.26380 0.50223 0.23470 0.44955 0.76812 0.58526
36 0 4 0.76604 0.28556 0.48048 0.23470 0.44955 0.75160 0.59813
37 0 3 0.76604 0.31402 0.45202 0.23470 0.44955 0.73051 0.61540
38 0 2 0.76604 0.35176 0.41428 0.23470 0.44955 0.70345 0.63907
39 0 2 0.76604 0.39333 0.37271 0.23470 0.44955 0.67481 0.66619
40 1 1 1.76604 0.43709 1.32895 1.02717 0.00000 0.64591 0.00000
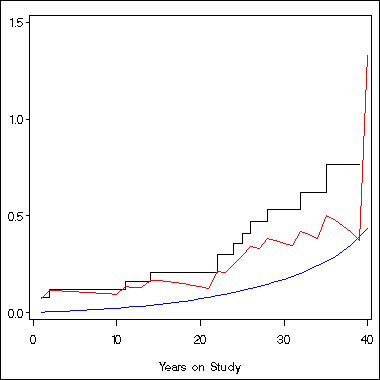
axis1 order = (0 to 1.5 by .5) label=(' ') minor = none;
axis2 order = (0 to 40 by 10) label=('Years on Study') minor = none;
symbol1 i = stepjl c = black;
symbol2 i = join c = blue;
symbol3 i = join c = red;
proc gplot data = temp;
plot h*time = 1 theta*time = 2 a*time = 3 /overlay vaxis = axis1 haxis=axis2;
run;
quit;
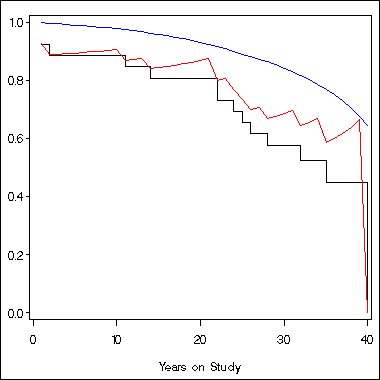
axis1 order = (0 to 1 by .2) label=(' ') minor = none;
axis2 order = (0 to 40 by 10) label=('Years on Study') minor = none;
symbol1 i = stepjl c = black;
symbol2 i = join c = blue;
symbol3 i = join c = red;
proc gplot data = temp;
plot s1*time = 1 survival*time = 2 sc*time = 3 /overlay vaxis = axis1
haxis=axis2;
run;
quit;
Section 6.4 Bayesian Nonparametric Methods
Under construction.