Section 12.2: Weibull Distribution
A data step creates a data set called sec1_9 and it can be downloaded here. We will use this data set in Example 12. 1 on page 377 for allo group. The analysis for auto group will be almost identical with the only change on the where statement. We omit the second analysis here.
proc lifereg data = sec1_9;
model time*ind(0)= /covb distribution=weibull;
where type = 1;
ods output ParameterEstimates = test;
ods output covB = covB;
run;
data test;
set test;
if parameter ~= "cons" & parameter ~= "Weibull Shape";
run;
proc iml;
use covB;
read all var {Intercept Scale};
x = Intercept || Scale ;
start grd(g); /*creating the gradient matrix corresponding to the transform*/
grdn = j(2, 2, 0);
grdn[1,1] = - exp(-g[1]/g[2])/g[2];
grdn[1,2] = (exp(-g[1]/g[2])*g[1])/(g[2]**2);
grdn[2,2] = -1/(g[2]**2);
return (grdn) ;
finish grd;
use test;
read all var {parameter estimate};
est = estimate;
parms = parameter;
mytet = grd(est);
print "Variance-Covariance Matrix";
covb= mytet*x*t(mytet);
print covb;
newvar = sqrt(diag(mytet*x*t(mytet))); /*delta method to calculate the variance*/
gnew = j(2, 1, 0);
gstd = j(2, 1, 0);
do i = 1 to 2; /*pulling out the standard error*/
gstd[i]=newvar[i,i];
end;
gnew[1] = exp(-est[1]/est[2]); /*doing the transformation*/
gnew[2] = 1/est[2];
print "Transformed Parameter Estimate";
print gnew[rowname = parms colname = "Parameter Estimate" label=" " format=8.3]
gstd[colname = " Standard Error" label = " " format=8.3];
quit;
The LIFEREG Procedure
Model Information
Data Set WORK.SEC1_9
Dependent Variable Log(time)
Censoring Variable ind
Censoring Value(s) 0
Number of Observations 50
Noncensored Values 22
Right Censored Values 28
Left Censored Values 0
Interval Censored Values 0
Name of Distribution Weibull
Log Likelihood -72.8790866
Analysis of Parameter Estimates
Standard 95% Confidence Chi-
Parameter DF Estimate Error Limits Square Pr > ChiSq
Intercept 1 4.2543 0.4782 3.3171 5.1915 79.16 <.0001
Scale 1 1.9444 0.3679 1.3420 2.8173
Weibull Scale 1 70.4075 33.6656 27.5813 179.7314
Weibull Shape 1 0.5143 0.0973 0.3549 0.7452
Estimated Covariance Matrix
Intercept Scale
Intercept 0.228631 0.087660
Scale 0.087660 0.135335
From Proc IML
Variance-Covariance Matrix
COVB
0.0016396 -0.00318
-0.00318 0.0094681
Transformed Parameter Estimate
Parameter Estimate Standard Error
Intercept 0.112 0.040
Scale 0.514 0.097
Example 12. 2, Table 12.1 and Table 12.2 on page 379 and page 380. This example uses a data set described in section 1.8. We create the data set here and call it larynx.
data table12_1; set larynx_cancer; z1 = (stage = 2); z2 = (stage = 3); z3 = (stage = 4); run; proc lifereg data = table12_1; model time*death(0)= z1 z2 z3 age / covb distribution=weibull; ods output ParameterEstimates = test; ods output covB = covB; run;
The LIFEREG Procedure
Analysis of Parameter Estimates
Standard 95% Confidence Chi-
Parameter DF Estimate Error Limits Square Pr > ChiSq
Intercept 1 3.5288 0.9041 1.7567 5.3008 15.23 <.0001
z1 1 -0.1477 0.4076 -0.9465 0.6511 0.13 0.7171
z2 1 -0.5866 0.3199 -1.2136 0.0405 3.36 0.0668
z3 1 -1.5441 0.3633 -2.2561 -0.8321 18.07 <.0001
age 1 -0.0175 0.0128 -0.0425 0.0076 1.87 0.1717
Scale 1 0.8848 0.1084 0.6960 1.1250
Weibull Shape 1 1.1301 0.1384 0.8889 1.4368
Table 12.2 based on the previous output and delta method shown on page 378.
proc iml;
use covB;
read all var {Intercept z1 z2 z3 age Scale};
x = Intercept || z1 || z2 || z3 || age || Scale ;
start grd(g); /*creating the gradient matrix corresponding to the transform*/
gdim = nrow(g);
grdn = j(gdim, gdim, 0);
grdn[1,1] = - exp(-g[1]/g[gdim])/g[gdim];
grdn[1,gdim] = (exp(-g[1]/g[gdim])*g[1])/(g[gdim]**2);
do i = 2 to gdim - 1;
grdn[i, gdim]=g[i]/(g[gdim]**2);
grdn[i,i] = - 1/g[gdim];
end;
grdn[gdim,gdim] = -1/(g[gdim]**2);
return (grdn) ;
finish grd;
use test;
read all var {parameter estimate};
est = estimate;
r = nrow(est);
g = est[1:r-1, 1];
parm = parameter;
parms = parm[1:r-1,1];
mytet = grd(g);
newvar = sqrt(diag(mytet*x*t(mytet))); /*delta method to calculate the variance*/
gnew = j(r-1, 1, 0);
gstd = j(r-1, 1, 0);
do i = 1 to r-1; /*pull out the standard error*/
gstd[i]=newvar[i,i];
end;
gnew[1] = exp(-g[1]/g[r-1]); /*doing the transformation*/
gnew[r-1] = 1/g[r-1];
do i = 2 to r-2;
gnew[i] = - g[i]/g[r-1];
end;
print "Transformed Parameter Estimate";
print gnew[rowname = parms colname = "Parameter Estimate" label=" " format=8.3]
gstd[colname = " Standard Error" label = " " format=8.3];
quit;
Transformed Parameter Estimate
Parameter Estimate Standard Error
Intercept 0.019 0.019
z1 0.167 0.461
z2 0.663 0.356
z3 1.745 0.415
age 0.020 0.014
Scale 1.130 0.138
Section 12.3: Log Logistic Distribution
Example 12.1 (continued) on page 382. We will only do the analysis for allo group. The analysis for auto group will be nearly identical.
proc lifereg data = sec1_9;
model time*ind(0)= /covb distribution=llogit;
where type = 1;
ods output ParameterEstimates = test;
ods output covB = covB;
run;
data test;
set test;
if parameter ~= "cons";
run;
proc iml;
use covB;
read all var {Intercept Scale};
x = Intercept || Scale ;
start grd(g); /*creating the gradient matrix corresponding to the transform*/
grdn = j(2, 2, 0);
grdn[1,1] = - exp(-g[1]/g[2])/g[2];
grdn[1,2] = (exp(-g[1]/g[2])*g[1])/(g[2]**2);
grdn[2,2] = -1/(g[2]**2);
return (grdn) ;
finish grd;
use test;
read all var {parameter estimate};
est = estimate;
parms = parameter;
mytet = grd(est);
print "Variance-Covariance Matrix";
covb= mytet*x*t(mytet);
print covb;
newvar = sqrt(diag(mytet*x*t(mytet))); /*delta method to calculate the variance*/
gnew = j(2, 1, 0);
gstd = j(2, 1, 0);
do i = 1 to 2; /*pulling out the standard error*/
gstd[i]=newvar[i,i];
end;
gnew[1] = exp(-est[1]/est[2]); /*doing the transformation*/
gnew[2] = 1/est[2];
print "Transformed Parameter Estimate";
print gnew[rowname = parms colname = "Parameter Estimate" label=" " format=8.3]
gstd[colname = " Standard Error" label = " " format=8.3];
quit;
The LIFEREG Procedure
Model Information
Data Set WORK.SEC1_9
Dependent Variable Log(time)
Censoring Variable ind
Censoring Value(s) 0
Number of Observations 50
Noncensored Values 22
Right Censored Values 28
Left Censored Values 0
Interval Censored Values 0
Name of Distribution LLogistic
Log Likelihood -71.72331008
Analysis of Parameter Estimates
Standard 95% Confidence Chi-
Parameter DF Estimate Error Limits Square Pr > ChiSq
Intercept 1 3.4429 0.4760 2.5099 4.3759 52.31 <.0001
Scale 1 1.5839 0.2926 1.1029 2.2748
Estimated Covariance Matrix
Intercept Scale
Intercept 0.226623 0.058140
Scale 0.058140 0.085586
Variance-Covariance Matrix
COVB
0.0019512 -0.003661
-0.003661 0.0135976
Transformed Parameter Estimate
Parameter Estimate Standard Error
Intercept 0.114 0.044
Scale 0.631 0.117
Example 12. 2 (continued).
proc lifereg data = table12_1;
model time*death(0)= z1 z2 z3 age / covb distribution=llogit;
ods output ParameterEstimates = test;
ods output covB = covB;
run;
proc iml;
use covB;
read all var {Intercept z1 z2 z3 age Scale};
x = Intercept || z1 || z2 || z3 || age || Scale ;
start grd(g); /*creating the gradient matrix corresponding to the transform*/
gdim = nrow(g);
grdn = j(gdim, gdim, 0);
grdn[1,1] = - exp(-g[1]/g[gdim])/g[gdim];
grdn[1,gdim] = (exp(-g[1]/g[gdim])*g[1])/(g[gdim]**2);
do i = 2 to gdim - 1;
grdn[i, gdim]=g[i]/(g[gdim]**2);
grdn[i,i] = - 1/g[gdim];
end;
grdn[gdim,gdim] = -1/(g[gdim]**2);
return (grdn) ;
finish grd;
use test;
read all var {parameter estimate};
est = estimate;
parm = parameter;
r = nrow(est);
mytet = grd(est);
newvar = sqrt(diag(mytet*x*t(mytet))); /*delta method to calculate the variance*/
gnew = j(r, 1, 0);
gstd = j(r, 1, 0);
do i = 1 to r; /*pull out the standard error*/
gstd[i]=newvar[i,i];
end;
gnew[1] = exp(-est[1]/est[r]); /*doing the transformation*/
gnew[r] = 1/est[r];
do i = 2 to r-1;
gnew[i] = - est[i]/est[r];
end;
print "Transformed Parameter Estimate";
print gnew[rowname = parm colname = "Parameter Estimate" label=" " format=8.3]
gstd[colname = " Standard Error" label = " " format=8.3];
quit;
The LIFEREG Procedure
Model Information
Data Set WORK.TABLE12_1
Dependent Variable Log(time)
Censoring Variable death
Censoring Value(s) 0
Number of Observations 90
Noncensored Values 50
Right Censored Values 40
Left Censored Values 0
Interval Censored Values 0
Name of Distribution LLogistic
Log Likelihood -108.1923738
Type III Analysis of Effects
Wald
Effect DF Chi-Square Pr > ChiSq
z1 1 0.0917 0.7621
z2 1 5.1844 0.0228
z3 1 17.2161 <.0001
The LIFEREG Procedure
Type III Analysis of Effects
Wald
Effect DF Chi-Square Pr > ChiSq
age 1 1.1995 0.2734
Analysis of Parameter Estimates
Standard 95% Confidence Chi-
Parameter DF Estimate Error Limits Square Pr > ChiSq
Intercept 1 3.1022 0.9527 1.2350 4.9694 10.60 0.0011
z1 1 -0.1257 0.4152 -0.9395 0.6881 0.09 0.7621
z2 1 -0.8057 0.3539 -1.4993 -0.1122 5.18 0.0228
z3 1 -1.7661 0.4257 -2.6004 -0.9319 17.22 <.0001
age 1 -0.0151 0.0138 -0.0421 0.0119 1.20 0.2734
Scale 1 0.7152 0.0860 0.5651 0.9053
Transformed Parameter Estimate
Parameter Estimate Standard Error
Intercept 0.013 0.018
z1 0.176 0.581
z2 1.127 0.498
z3 2.469 0.632
age 0.021 0.019
Scale 1.398 0.168
Section 12.4: Other Parametric Models
Example 12.1 (continued), Table 12. 5 on page 387. We use the ODS feature of SAS 8 here to put all the output data sets from multiple procedures into one data set.
ods output ModelInfo (match_all=mymatch persist=proc) = table12_5; proc lifereg data = sec1_9; model time*ind(0)= / distribution=exponential; by type; run; proc lifereg data = sec1_9; model time*ind(0)=/ distribution=weibull; by type; run; proc lifereg data = sec1_9; model time*ind(0)= / distribution=llogistic; by type; run; proc lifereg data = sec1_9; model time*ind(0)= / distribution=lnormal; by type; run; proc lifereg data = sec1_9; model time*ind(0)= / distribution=gamma; by type; run; ods output close; data test (rename=(nvalue1=value)); set &mymatch; if label1="Name of Distribution" or label1 = "Log Likelihood"; distribution = lag(cvalue1); if nvalue1 ~= .; drop label1 _proc_ _run_ cvalue1; run; data test2; set test; if distribution="Exponential" then aic = -2*value + 2*( 1 ); else if distribution="Gamma" then aic = -2*value + 2*( 1 + 2); else aic = -2*value + 2*( 1 + 1); run; proc print data=test2 noobs; run; type value distribution aic 1 -81.204342 Exponential 164.409 2 -68.653867 Exponential 139.308 1 -72.879087 Weibull 149.758 2 -68.420282 Weibull 140.841 1 -71.723310 LLogistic 147.447 2 -67.146462 LLogistic 138.293 1 -71.186940 Lognormal 146.374 2 -66.847574 Lognormal 137.695 1 -70.892978 Gamma 147.786 2 -66.780969 Gamma 139.562
The last part of the output related to Gamma distribution is obtained by running the lifereg procedure and computing the Wald test statistic manually.
ods output ParameterEstimates (match_all=bytype persist=proc) = table12_5b; proc lifereg data = sec1_9; model time*ind(0)= / distribution=gamma; by type; run; ods output close; data waldtest; set &bytype; keep estimate stderr test0 test1; if parameter="Shape"; test0 = 1- probchi(estimate**2/stderr**2,1); test1 = 1- probchi((estimate-1)**2/stderr**2,1); run; proc print data=waldtest noobs; run; Estimate StdErr test0 test1 -0.6331 0.8264 0.44363 0.048146 -0.2613 0.7253 0.71865 0.08202
The bottom table on page 387.
data sec1_9b; set sec1_9; z1 = type - 1; run; proc lifereg data = sec1_9b; model time*ind(0)=z1 /distribution=lnormal; run;
The LIFEREG Procedure
Model Information
Data Set WORK.SEC1_9B
Dependent Variable Log(time)
Censoring Variable ind
Censoring Value(s) 0
Number of Observations 101
Noncensored Values 50
Right Censored Values 51
Left Censored Values 0
Interval Censored Values 0
Name of Distribution Lognormal
Log Likelihood -141.8636186
Type III Analysis of Effects
Wald
Effect DF Chi-Square Pr > ChiSq
z1 1 0.0133 0.9080
Analysis of Parameter Estimates
Standard 95% Confidence Chi-
Parameter DF Estimate Error Limits Square Pr > ChiSq
Intercept 1 3.1774 0.3552 2.4813 3.8735 80.04 <.0001
z1 1 0.0535 0.4629 -0.8537 0.9607 0.01 0.9080
Scale 1 2.0843 0.2299 1.6791 2.5873
Table 12.6 on page 388, making use of the ODS feature and proc tabulate for a nicer output.
ods output ParameterEstimates (match_all=bydist persist=proc) = table12_6;
proc lifereg data = table12_1;
model time*death(0)= z1 z2 z3 age / distribution=exponential;
run;
proc lifereg data = table12_1;
model time*death(0)= z1 z2 z3 age / distribution=weibull;
run;
proc lifereg data = table12_1;
model time*death(0)= z1 z2 z3 age / distribution=llogistic;
run;
proc lifereg data = table12_1;
model time*death(0)= z1 z2 z3 age / distribution=lognormal;
run;
proc lifereg data = table12_1;
model time*death(0)= z1 z2 z3 age / distribution=gamma;
run;
ods output close;
data table126;
set &bydist;
retain group 0;
keep parameter estimate stderr group;
if parameter = "Intercept" then group= group+1;
run;
proc format;
value group 1 = "Exponential"
2 = "Weibull"
3 = "Log Logistic"
4 = "Log Normal"
5 = "Gamma";
run;
options nocenter FORMCHAR='|----|+|---+=|-/<>*';
proc tabulate data=table126;
format group group.;
class group parameter;
var estimate stderr;
table parameter='', group=' '*(estimate='Est' stderr='SE')*sum=' '*f=5.3/RTS=13;
run;
-------------------------------------------------------------------------
| | | | Log | | |
| |Exponential| Weibull | Logistic |Log Normal | Gamma |
| |-----------+-----------+-----------+-----------+-----------|
| | Est | SE | Est | SE | Est | SE | Est | SE | Est | SE |
|-----------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----|
|Intercept |3.755|0.990|3.529|0.904|3.102|0.953|3.383|0.936|3.453|0.944|
|-----------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----|
|Scale |1.000|0.000|0.885|0.108|0.715|0.086|1.264|0.135|1.104|0.257|
|-----------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----|
|Shape | .| .| .| .| .| .| .| .|0.458|0.584|
|-----------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----|
|Weibull | | | | | | | | | | |
|Shape |1.000|0.000|1.130|0.138| .| .| .| .| .| .|
|-----------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----|
|age |-.020|0.014|-.017|0.013|-.015|0.014|-.018|0.014|-.018|0.014|
|-----------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----|
|z1 |-.146|0.460|-.148|0.408|-.126|0.415|-.199|0.442|-.158|0.431|
|-----------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----|
|z2 |-.648|0.355|-.587|0.320|-.806|0.354|-.900|0.363|-.758|0.394|
|-----------+-----+-----+-----+-----+-----+-----+-----+-----+-----+-----|
|z3 |-1.64|0.399|-1.54|0.363|-1.77|0.426|-1.86|0.443|-1.73|0.449|
------------------------------------------------------------------------|
The rest of the output from Table 12.6 can be obtained from the following.
ods output ModelInfo (match_all=bydist persist=proc) = table126_mod;
proc lifereg data = table12_1;
model time*death(0)= z1 z2 z3 age / distribution=exponential;
run;
proc lifereg data = table12_1;
model time*death(0)= z1 z2 z3 age / distribution=weibull;
run;
proc lifereg data = table12_1;
model time*death(0)= z1 z2 z3 age / distribution=llogistic;
run;
proc lifereg data = table12_1;
model time*death(0)= z1 z2 z3 age / distribution=lognormal;
run;
proc lifereg data = table12_1;
model time*death(0)= z1 z2 z3 age / distribution=gamma;
run;
ods output close;
data table126btm;
set &bydist;
lagv = lag(cvalue1);
if label1 = "Log Likelihood" or label1="Name of Distribution";
keep nvalue1 aic;
if lagv = "Exponential" then aic = -2*nvalue1 + 2*( 1+4 );
else if lagv = "Gamma" then aic = -2*nvalue1 + 2*( 1 + 2 +4);
else aic = -2*nvalue1 + 2*( 1 + 1 +4);
if nvalue1 ~=.;
run;
data table126btm1;
set table126btm;
id = _n_;
run;
proc format;
value group 1 = "Exponential"
2 = "Weibull"
3 = "Log Logistic"
4 = "Log Normal"
5 = "Gamma";
run;
proc print data=table126btm1(rename=(nvalue1=LogL)) noobs;
format id group.;
var id LogL AIC;
run;
Obs id LogL aic 1 Exponential -108.501123 227.002 2 Weibull -108.026745 228.053 3 Log Logistic -108.192374 228.385 4 Log Normal -107.995034 227.990 5 Gamma -107.680270 229.361
Section 12.5: Diagnostic Methods for Parametric Models
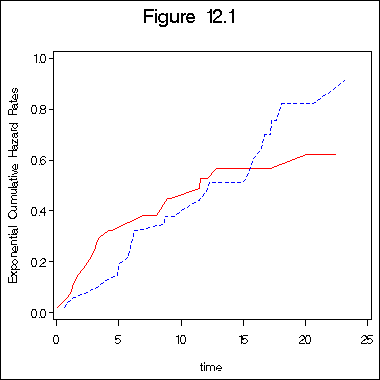
Example 12.1 (continued) Figure 12.1 on page 390. In this example, we first create a data set containing the estimates on survivals for both groups. Then we create all the necessary variables for different distributions of different plots.
proc phreg data =sec1_9; model time*ind(0) = ; where type = 1; output out = surv1 survival=surv1 /method = ch ; run; proc phreg data =sec1_9; model time*ind(0) = ; where type = 2; output out = surv2 survival=surv2 /method = ch ; run; data surv1_9; merge surv1 surv2; by time; haz1 = -log (surv1);/*Exponential*/ haz2 = -log (surv2); lghaz1 = log(haz1); /*Weibull*/ lghaz2 = log(haz2); lgtime = log(time); lnhaz1 = probit(1-exp(-haz1)); lnhaz2 = probit(1-exp(-haz2)); lohaz1 = log(exp(haz1)-1); lohaz2 = log(exp(haz2)-1); run; title "Figure 12.1"; symbol1 c=red i=l1p l=1; symbol2 c=blue i=l1p l=2 ; axis1 order =(0 to 25 by 5) minor = none; axis2 order =(0 to 1 by .2) minor = none label =(a=90); proc gplot data = surv1_9; plot haz1*time = 1 haz2*time =2 /overlay haxis = axis1 vaxis=axis2; label haz1 = "Exponential Cumulative Hazard Rates"; run; quit;
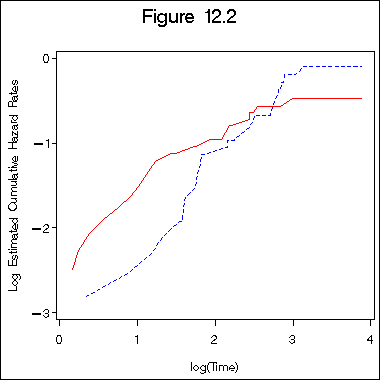
Figure 12.2 on page 391 on Weibull distribution.
title "Figure 12.2"; symbol1 c=red i=l1p l=1; symbol2 c=blue i=l1p l=2 ; axis1 order =(0 to 4 by 1) minor = none; axis2 order =(-3 to 0 by 1) minor = none label =(a=90); proc gplot data = surv1_9; plot lghaz1*lgtime = 1 lghaz2*lgtime =2 /overlay haxis = axis1 vaxis=axis2; label lghaz1 = "Log Estimated Cumulative Hazard Rates"; label lgtime ="log(Time)"; run; quit;
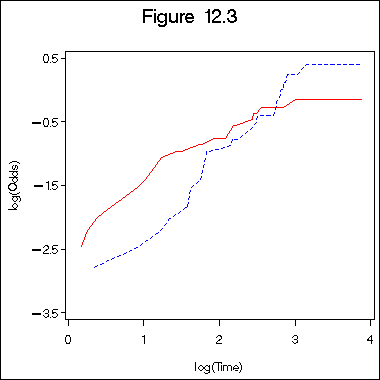
Figure 12.3 on page 392 of log logistic plot. The variables in the proc gplot are defined earlier.
title "Figure 12.3"; symbol1 c=red i=l1p l=1; symbol2 c=blue i=l1p l=2 ; axis1 order =(0 to 4 by 1) minor = none; axis2 order =(-3.5 to 0.5 by 1) minor = none label =(a=90); proc gplot data = surv1_9; plot lohaz1*lgtime = 1 lohaz2*lgtime =2 /overlay haxis = axis1 vaxis=axis2; label lohaz1 = "log(Odds)"; label lgtime="log(Time)"; run; quit;
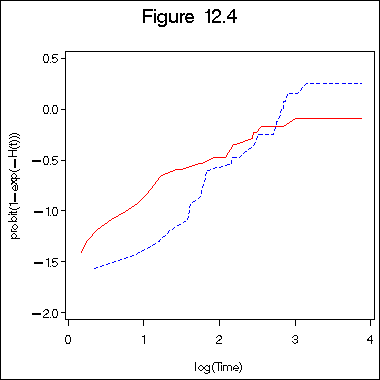
Figure 12. 4 on page 393 of log normal hazard plot.
title "Figure 12.4"; symbol1 c=red i=l1p l=1; symbol2 c=blue i=l1p l=2 ; axis1 order =(0 to 4 by 1) minor = none; axis2 order =(-2 to 0.5 by .5) minor = none label =(a=90); proc gplot data = surv1_9; plot lnhaz1*lgtime = 1 lnhaz2*lgtime =2 /overlay haxis = axis1 vaxis=axis2; label lnhaz1 = "probit(1-exp(-H(t)))"; label lgtime="log(Time)"; run; quit;
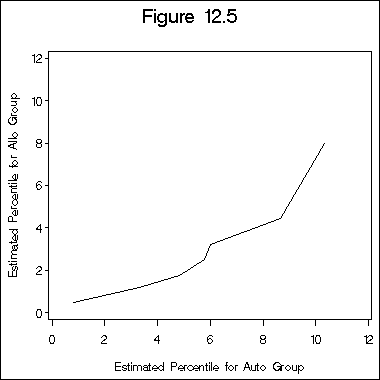
Figure 12.5 on page 394 is a quantile-quantile plot.
proc lifetest data =sec1_9 outsurv=surv1 (keep=time survival); time time*ind(0) ; where type = 1; run; proc lifetest data =sec1_9 outsurv=surv2 (keep=time survival); time time*ind(0) ; where type = 2; run; data type1; set surv1; retain time1 0; do i = 1 to 7; if .05*(i-1) < 1- survival <.05*i then do p1=i; time1 = time; end; end; if p1 ~=.; keep time1 p1 ; run; proc sql; create table type1p as select max(time1) as time, p1 as p from type1 group by p1; quit; data type2; set surv2; retain time2 0; do i = 1 to 7; if .05*(i-1) < 1- survival <.05*i then do p2=i; time2 = time; end; end; if p2 ~=.; keep time2 p2 ; run; proc sql; create table type2p as select max(time2) as time, p2 as p from type2 group by p2; quit; proc sql; create table comb2 as select s1.time as time1, s2.time as time2 from type1p as s1, type2p as s2 where s1.p=s2.p; quit; symbol i = join v=none; axis1 order=(0 to 12 by 2) minor=none; axis2 order=(0 to 12 by 2) minor=none label=(a=90); title "Figure 12.5"; proc gplot data=comb2; plot time1*time2 /haxis=axis1 vaxis=axis2; label time1 ="Estimated Percentile for Allo Group"; label time2 = "Estimated Percentile for Auto Group"; run; quit;
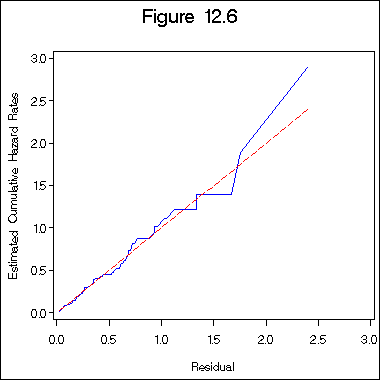
Figure 12.6 on page 395 of Cox-Snell residual plot.
proc reliability data =table12_1;
distribution exponential;
model time*death(0) = z1 z2 z3 age /obstats (survival) ;
ods output ModObstats = figure12_6;
run;
data figure12_6a;
set figure12_6;
h = -log(surv);
run;
proc phreg data = figure12_6a ;
model h*death(0) = ;
output out = figure12_6b logsurv = ls /method = ch;
run;
data figure12_6c;
set figure12_6b;
haz = - ls;
run;
proc sort data = figure12_6c;
by h;
run;
title "Figure 12.6";
axis1 order = (0 to 3 by .5) minor = none;
axis2 order = (0 to 3 by .5) minor = none label = ( a=90);
symbol1 i = i=l1p c= blue;
symbol2 i = join c = red l = 3;
proc gplot data = figure12_6c;
plot haz*h =1 h*h =2 /overlay haxis=axis1 vaxis= axis2;
label haz = "Estimated Cumulative Hazard Rates";
label h = "Residual";
run;
quit;
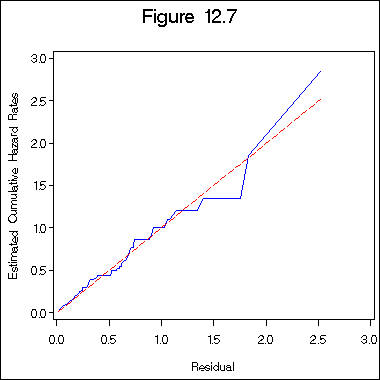
Figure 12.7 on page 396 of the Weibull regression model.
proc reliability data =table12_1;
distribution weibull;
model time*death(0) = z1 z2 z3 age /obstats (survival) ;
ods output ModObstats = figure12_6;
run;
data figure12_6a;
set figure12_6;
h = -log(surv);
run;
proc phreg data = figure12_6a ;
model h*death(0) = ;
output out = figure12_6b logsurv = ls /method = ch;
run;
data figure12_6c;
set figure12_6b;
haz = - ls;
run;
proc sort data = figure12_6c;
by h;
run;
title "Figure 12.7";
axis1 order = (0 to 3 by .5) minor = none;
axis2 order = (0 to 3 by .5) minor = none label = ( a=90);
symbol1 i = i=l1p c= blue;
symbol2 i = join c = red l = 3;
proc gplot data = figure12_6c;
plot haz*h =1 h*h =2 /overlay haxis=axis1 vaxis= axis2;
label haz = "Estimated Cumulative Hazard Rates";
label h = "Residual";
run;
quit;
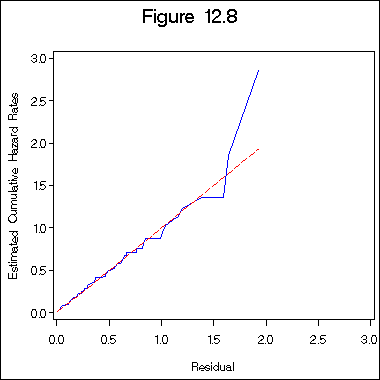
Figure 12.8 on page 397 of log logistic regression model.
proc reliability data =table12_1;
distribution llogit;
model time*death(0) = z1 z2 z3 age /obstats (survival) ;
ods output ModObstats = figure12_6;
run;
data figure12_6a;
set figure12_6;
h = -log(surv);
run;
proc phreg data = figure12_6a ;
model h*death(0) = ;
output out = figure12_6b logsurv = ls /method = ch;
run;
data figure12_6c;
set figure12_6b;
haz = - ls;
run;
proc sort data = figure12_6c;
by h;
run;
title "Figure 12.8";
axis1 order = (0 to 3 by .5) minor = none;
axis2 order = (0 to 3 by .5) minor = none label = ( a=90);
symbol1 i = i=l1p c= blue;
symbol2 i = join c = red l = 3;
proc gplot data = figure12_6c;
plot haz*h =1 h*h =2 /overlay haxis=axis1 vaxis= axis2;
label haz = "Estimated Cumulative Hazard Rates";
label h = "Residual";
run;
quit;
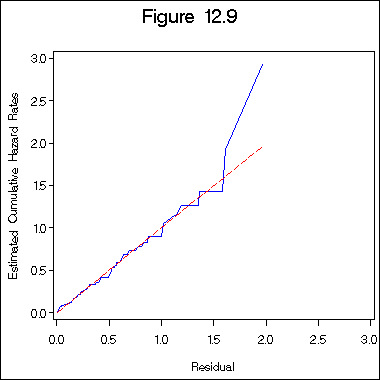
Figure 12.9 on page 398 of log normal regression model.
proc reliability data =table12_1;
distribution lognormal;
model time*death(0) = z1 z2 z3 age /obstats (survival) ;
ods output ModObstats = figure12_6;
run;
data figure12_6a;
set figure12_6;
h = -log(surv);
run;
proc phreg data = figure12_6a ;
model h*death(0) = ;
output out = figure12_6b logsurv = ls /method = ch;
run;
data figure12_6c;
set figure12_6b;
haz = - ls;
run;
proc sort data = figure12_6c;
by h;
run;
title "Figure 12.9";
axis1 order = (0 to 3 by .5) minor = none;
axis2 order = (0 to 3 by .5) minor = none label = ( a=90);
symbol1 i = i=l1p c= blue;
symbol2 i = join c = red l = 3;
proc gplot data = figure12_6c;
plot haz*h =1 h*h =2 /overlay haxis=axis1 vaxis= axis2;
label haz = "Estimated Cumulative Hazard Rates";
label h = "Residual";
run;
quit;
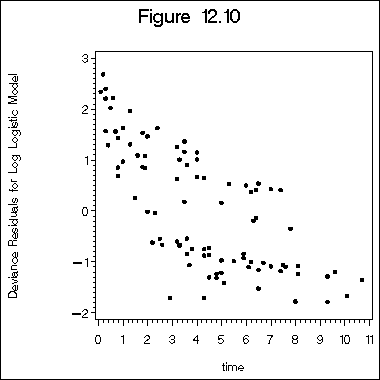
Figure 12.10 on page 399 of deviance residuals.
proc reliability data =table12_1; distribution llogit; model time*death(0) = z1 z2 z3 age /obstats (DRESID) ; ods output ModObstats = figure12_6; run; proc sort data=figure12_6; by time; run; symbol v=dot h=1.5 c=black i=none; axis1 order = (-2 to 3 by 1) label=(a = 90) ; title "Figure 12.10"; proc gplot data = figure12_6; plot dresid*time /vaxis=axis1; label dresid="Deviance Residuals for Log Logistic Model"; run; quit;