Section 4.2: Estimators of the Survival and Cumulative Hazard Functions for Right-Censored Data
data sec1_2; input pair status time_p time_mp censor; cards; 1 1 1 10 1 2 2 22 7 1 3 2 3 32 0 4 2 12 23 1 5 2 8 22 1 6 1 17 6 1 7 2 2 16 1 8 2 11 34 0 9 2 8 32 0 10 2 12 25 0 11 2 2 11 0 12 1 5 20 0 13 2 4 19 0 14 2 15 6 1 15 2 8 17 0 16 1 23 35 0 17 1 5 6 1 18 2 11 13 1 19 2 4 9 0 20 2 1 6 0 21 2 8 10 0 ; run;
Table 4.1A and Table 4.1B on page 85 shown together in the SAS output. Since this is explicitly a counting procedure, we use a data step here, instead of any procedures.
options nocenter nonumber nodate; proc sql; create table raw_data as select time_mp, sum(censor) as num_event, count(time_mp) as sub_total from sec1_2 group by time_mp; quit; data raw_data1; set raw_data ; total1 = lag(sub_total); retain num_left 21; if _n_ > 1 then do; num_left = - total1 + num_left; end; if num_event~=0; retain surv 1 delta 0; surv = surv*(1-num_event/num_left); delta= delta + num_event/(num_left*(num_left-num_event)); var =(surv**2)*delta; stderr = var**.5; keep time_mp num_event num_left surv delta var stderr; run; title "Table 4.1A and Table4.1B"; proc print data = raw_data1 noobs; run;
Table 4.1A and Table4.1B
num_
time_mp event num_left surv delta var stderr
6 3 21 0.85714 0.007937 0.005831 0.07636
7 1 17 0.80672 0.011613 0.007558 0.08694
10 1 15 0.75294 0.016375 0.009283 0.09635
13 1 12 0.69020 0.023951 0.011409 0.10681
16 1 11 0.62745 0.033042 0.013008 0.11405
22 1 7 0.53782 0.056851 0.016444 0.12823
23 1 6 0.44818 0.090184 0.018115 0.13459
Table 4.2 on page 86 based on the data set raw_data1 created in the previous example.
data table4_2; set raw_data1; retain h sigma2 0; h = h + num_event/num_left; sigma2 = sigma2 + num_event/num_left**2; stderr=sigma2**.5; run; title "Table 4.2"; proc print data = table4_2 noobs; var time_mp h sigma2 stderr; run;
Table 4.2
time_mp h sigma2 stderr
6 0.14286 0.006803 0.08248
7 0.20168 0.010263 0.10131
10 0.26835 0.014707 0.12127
13 0.35168 0.021652 0.14715
16 0.44259 0.029916 0.17296
22 0.58545 0.050324 0.22433
23 0.75211 0.078102 0.27947
Figure 4.1A on page 87 comparing the Nelson-Aalen and PL estimates.
data figure4_1a ; if _n_ =1 then do; time_mp = 0; surv=1; surv2=1; output; end; set table4_2 nobs=l; surv2=exp(-h); output; if _n_ = l then do ; time_mp=30; surv=surv; surv2 = surv2; output; end; run; symbol1 i=steplj c=blue; symbol2 i=steplj c=red l=4; axis1 label=(a=90) order=(0 to 1 by .2) minor=none; axis2 order=(0 to 30 by 10) minor=none; title "Figure 4.1A"; proc gplot data = figure4_1a; plot surv*time_mp = 1 surv2*time_mp = 2/overlay haxis=axis2 vaxis=axis1; label time_mp="Weeks"; label surv="Survival Function"; run; quit;
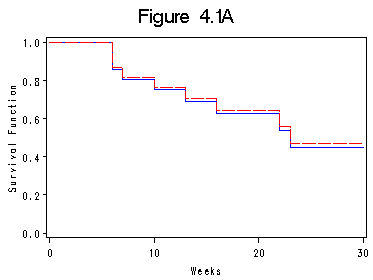
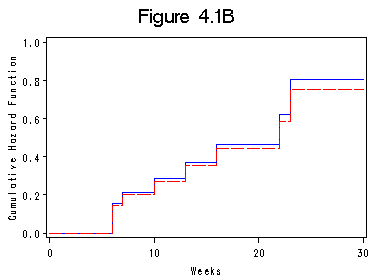
Figure 4.1B on page 88.
data figure4_1b ; if _n_ =1 then do; time_mp = 0; h_na=0; h_pl=0; output; end; set table4_2 nobs=l; h_pl = -log(surv); h_na = h ; output; if _n_ = l then do ; time_mp=30; h_na =h_na; h_pl = h_pl; output; end; run; title "Figure 4.1B"; symbol1 i=steplj c=blue; symbol2 i=steplj c=red l=4; axis1 label=(a=90) order=(0 to 1 by .2) minor=none; axis2 order=(0 to 30 by 10) minor=none; proc gplot data = figure4_1b; plot h_pl*time_mp = 1 h_na*time_mp = 2/overlay haxis=axis2 vaxis=axis1; label time_mp="Weeks"; label h_pl="Cumulative Hazard Function"; run; quit;
Table 4.3 on page 89 based on the bone marrow transplant data set. A data step creates a data set called bone_marrow and it can be downloaded here.
proc sql; create table raw_data3 as select t2, sum(dfree) as num_event, count(t2) as sub_total from bone_marrow where g = 1 group by t2; quit; data table4_3; set raw_data3 nobs = all; total1 = lag(sub_total); retain num_left 38; if _n_ > 1 then do; num_left = - total1 + num_left; end; retain surv 1 delta h sigma2 0; surv = surv*(1-num_event/num_left); delta= delta + num_event/(num_left*(num_left-num_event)); var =(surv**2)*delta; stderr = var**.5; h = h + num_event / num_left; sigma2 = sigma2 + num_event /(num_left)**2; stderrh = sigma2**.5; keep t2 num_event num_left surv stderr h stderrh; if num_event~=0 or _n_ = all; run; proc print data = table4_3 noobs; var t2 num_event num_left surv stderr h stderrh; run;
num_ t2 event num_left surv stderr h stderrh 1 1 38 0.97368 0.025967 0.02632 0.02632 55 1 37 0.94737 0.036224 0.05334 0.03772 74 1 36 0.92105 0.043744 0.08112 0.04685 86 1 35 0.89474 0.049784 0.10969 0.05487 104 1 34 0.86842 0.054836 0.13910 0.06226 107 1 33 0.84211 0.059153 0.16941 0.06924 109 1 32 0.81579 0.062886 0.20066 0.07597 110 1 31 0.78947 0.066135 0.23291 0.08253 122 2 30 0.73684 0.071434 0.29958 0.09505 129 1 28 0.71053 0.073570 0.33530 0.10153 172 1 27 0.68421 0.075405 0.37233 0.10808 192 1 26 0.65789 0.076960 0.41079 0.11472 194 1 25 0.63158 0.078252 0.45079 0.12149 230 1 23 0.60412 0.079522 0.49427 0.12904 276 1 22 0.57666 0.080509 0.53973 0.13681 332 1 21 0.54920 0.081223 0.58735 0.14486 383 1 20 0.52174 0.081672 0.63735 0.15325 418 1 19 0.49428 0.081860 0.68998 0.16203 466 1 18 0.46682 0.081788 0.74553 0.17129 487 1 17 0.43936 0.081457 0.80436 0.18111 526 1 16 0.41190 0.080862 0.86686 0.19159 609 1 14 0.38248 0.080260 0.93829 0.20447 662 1 13 0.35306 0.079296 1.01521 0.21846 2081 0 1 0.35306 0.079296 1.01521 0.21846
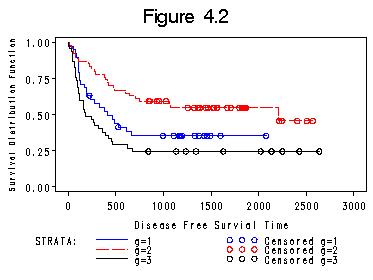
Figure 4.2 on page 90.
proc lifetest data = bone_marrow plots = (s) graphics; time t2*dfree(0); strata g; title "Figure 4.2"; symbol v= none; run;
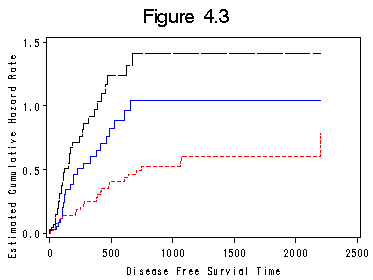
Figure 4.3 on page 91. Proc lifetest has an option for output the cumulative hazard rate plot. But the plot is not in the style of step functions. Here we introduce another way for creating the plot.
proc lifetest data = bone_marrow outsurv = figure4_3; time t2*dfree(0); strata g; run; proc sort data = figure4_3 out=figure4_3a; by t2; where survival~=.; proc transpose data = figure4_3a out= figure4_3b prefix=surv; format g 2.; by t2 ; id g ; var survival; run; data fig4_3; set figure4_3b ; retain h1-h3 0; if surv1 ~= . then h1 = -log(surv1); if surv2 ~= . then h2 = -log(surv2); if surv3 ~= . then h3 = -log(surv3); run; goptions reset = all; title "Figure 4.3"; symbol1 i = stepjl l = 1 c = blue; symbol2 i = stepjl l = 2 c = red; symbol3 i = stepjl l = 5 c = black; axis1 order = (0 to 2500 by 500) minor = none; axis2 order = (0.0 to 1.5 by .5) minor = none label = ( a= 90); proc gplot data = fig4_3; plot h1*t2 =1 h2*t2=2 h3*t2=3 /overlay haxis = axis1 vaxis = axis2; label h1 = "Estimated Cumulative Hazard Rate"; run; quit;
Section 4.3: Pointwise Confidence Intervals for Survival Function
Table 4.4. We only produced the first column for the ALL group. The other two groups will be the same. The proc sql part creates a data set that is used to in the next data step to create a life table. The last data step creates different types of confidence intervals.
proc sql;
create table table4_4_1 as
select t2, sum(dfree) as num_event, count(t2) as sub_total
from bone_marrow
where g = 1
group by t2;
quit;
data table4_4;
set table4_4_1 nobs = all;
total1 = lag(sub_total);
retain num_left 38;
if _n_ > 1 then do;
num_left = - total1 + num_left; end;
retain surv 1 delta h sigma2 0;
surv = surv*(1-num_event/num_left);
delta= delta + num_event/(num_left*(num_left-num_event));
var =(surv**2)*delta;
stderr = var**.5;
h = h + num_event / num_left;
sigma2 = sigma2 + num_event /(num_left)**2;
stderrh = sigma2**.5;
if num_event~=0 or _n_ = all;
run;
data table4_4_1a;
set table4_4;
if surv ~=. then sigma = stderr / surv;
md = probit(1-.05/2)*sigma ;
linearL = surv - md * surv;
linearU = surv + md * surv;
logL = surv**( 1 / (exp( md /log(surv))));
logU = surv**(exp( md /(log(surv))));
sinL = (sin(max(0, arsin(surv**.5) - .5 * md *(surv/(1-surv))**.5)))**2;
sinU = (sin(min(CONSTANT('PI') /2, arsin(surv**.5) + .5 * md *(surv/(1-surv))**.5)))**2;
run;
title;
proc print data = table4_4_1a noobs;
var t2 surv var stderr sigma;
var linearL linearU;
var logL logU ;
var sinL sinU;
where t2 = 332;
run;
t2 surv var stderr sigma 332 0.54920 .006597211 0.081223 0.14789 linearL linearU logL logU sinL sinU 0.39000 0.70839 0.37830 0.69110 0.39021 0.70319
Section 4.4 Confidence Bands for the Survival Function
Table 4.5 on page 102. We are going to input the confidence coefficient created in Appendix C manually in our data step. This calculation is based on the previous calculation on survival function estimate. So we are going to use the data set table4_4 created from last section. We omit the code for table 4.6 since we are going to do for Figure 4.5 below.
data table4_5_ep;
set table4_4;
if surv ~=. then sigma = stderr / surv;
md = 2.8826*sigma ;
linearL = surv - md * surv;
linearU = surv + md * surv;
logL = surv**( 1 / (exp( md /log(surv))));
logU = surv**(exp( md /(log(surv))));
sinL = (sin(max(0, arsin(surv**.5) - .5 * md *(surv/(1-surv))**.5)))**2;
sinU = (sin(min(CONSTANT('PI') /2, arsin(surv**.5) + .5 * md *(surv/(1-surv))**.5)))**2;
if 100 <=t2 <=600 ;
run;
proc print data=table4_5_ep noobs;
var t2 surv stderr sigma2 linearL linearU logL logU sinL sinU;
run;
t2 surv stderr sigma2 linearL linearU logL logU sinL sinU 104 0.86842 0.054836 0.003876 0.71035 1.02649 0.59893 0.96192 0.67650 0.98124 107 0.84211 0.059153 0.004794 0.67159 1.01262 0.57218 0.94848 0.64101 0.96975 109 0.81579 0.062886 0.005771 0.63451 0.99706 0.54531 0.93393 0.60715 0.95663 110 0.78947 0.066135 0.006811 0.59883 0.98011 0.51864 0.91841 0.57463 0.94216 122 0.73684 0.071434 0.009034 0.53093 0.94276 0.46648 0.88488 0.51292 0.90991 129 0.71053 0.073570 0.010309 0.49845 0.92260 0.44110 0.86702 0.48350 0.89235 172 0.68421 0.075405 0.011681 0.46685 0.90157 0.41623 0.84849 0.45491 0.87396 192 0.65789 0.076960 0.013160 0.43605 0.87974 0.39186 0.82933 0.42710 0.85479 194 0.63158 0.078252 0.014760 0.40601 0.85715 0.36801 0.80958 0.40002 0.83489 230 0.60412 0.079522 0.016651 0.37489 0.83335 0.34300 0.78869 0.37196 0.81382 276 0.57666 0.080509 0.018717 0.34458 0.80873 0.31869 0.76720 0.34472 0.79199 332 0.54920 0.081223 0.020984 0.31507 0.78333 0.29504 0.74510 0.31826 0.76944 383 0.52174 0.081672 0.023484 0.28631 0.75717 0.27206 0.72242 0.29256 0.74618 418 0.49428 0.081860 0.026254 0.25831 0.73025 0.24972 0.69915 0.26760 0.72221 466 0.46682 0.081788 0.029341 0.23106 0.70258 0.22803 0.67531 0.24337 0.69754 487 0.43936 0.081457 0.032801 0.20455 0.67417 0.20698 0.65088 0.21988 0.67216 526 0.41190 0.080862 0.036707 0.17881 0.64499 0.18660 0.62586 0.19712 0.64607
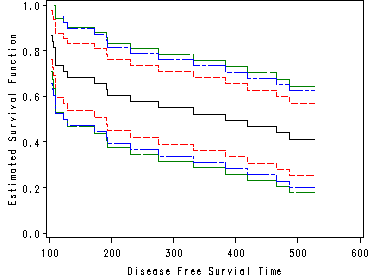
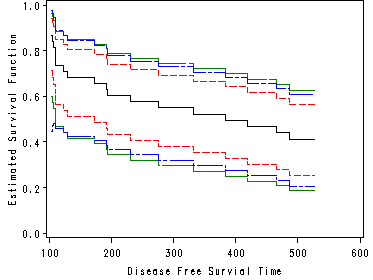
Figure 4.5 on page 104.
data figure4_5; set table4_4; if surv ~=. then sigma = stderr / surv; md = probit(1-.05/2)*sigma ; md1 = 2.8826*sigma ; md2 = 1.3211*(1+38*sigma2)/38**.5; pointL = surv - md * surv; pointU = surv + md * surv; epL = surv - md1*surv; epU = surv + md1*surv; hwL = surv - md2*surv; hwU = surv + md2*surv; if 100 <=t2 <=600 ; run; symbol1 value = none line = 1 i = stepjr color = black; symbol2 value = none line = 3 i = stepjr color = red; symbol3 value = none line = 3 i = stepjr color = red; symbol4 value = none line = 7 i = stepjr color = green; symbol5 value = none line = 7 i = stepjr color = green; symbol6 value = none line = 9 i = stepjr color = blue; symbol7 value = none line = 9 i = stepjr color = blue; proc gplot data=figure4_5; plot (surv pointU pointL epL epU hwL hwU )*t2 /overlay; run; quit;
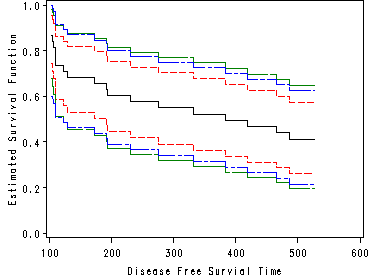
Figure 4.6 on page 105.
data figure4_6; set table4_4; if surv ~=. then sigma = stderr / surv; md = probit(1-.05/2)* sigma ; md1 = 2.8826*sigma ; md2 = 1.3211*(1+38*sigma2)/38**.5; pointL = surv**( 1 / (exp( md /log(surv)))); pointU = surv**(exp( md /(log(surv)))); epL = surv**( 1 / (exp( md1 /log(surv)))); epU = surv**(exp( md1 /(log(surv)))); hwL = surv**( 1 / (exp( md2 /log(surv)))); hwU = surv**(exp( md2 /(log(surv)))); if 100 <=t2 <=600 ; run; proc gplot data=figure4_6; plot (surv pointU pointL epL epU hwL hwU )*t2 /overlay haxis=axis1 vaxis=axis2; label surv="Estimated Survival Function"; run; quit;
Figure 4.6 on page 105.
data figure4_7;
set table4_4;
if surv ~=. then sigma = stderr / surv;
md = probit(1-.05/2)* sigma ;
md1 = 2.8826*sigma ;
md2 = 1.3211*(1+38*sigma2)/38**.5;
pointL = (sin(max(0, arsin(surv**.5) - .5 * md *(surv/(1-surv))**.5)))**2;
pointU = (sin(min(CONSTANT('PI') /2, arsin(surv**.5) + .5 * md *(surv/(1-surv))**.5)))**2;
epL = (sin(max(0, arsin(surv**.5) - .5 * md1 *(surv/(1-surv))**.5)))**2;
epU = (sin(min(CONSTANT('PI') /2, arsin(surv**.5) + .5 * md1 *(surv/(1-surv))**.5)))**2;
hwL = (sin(max(0, arsin(surv**.5) - .5 * md2 *(surv/(1-surv))**.5)))**2;
hwU = (sin(min(CONSTANT('PI') /2, arsin(surv**.5) + .5 * md2 *(surv/(1-surv))**.5)))**2;
if 100 <=t2 <=600 ;
run;
proc gplot data=figure4_7;
plot (surv pointU pointL epL epU hwL hwU )*t2 /overlay haxis=axis1 vaxis=axis2;
label surv="Estimated Survival Function";
run;
quit;
We omit the code for the rest of plots, since they are similar to what we have here.
Section 4.5 Point and Interval Estimates of the Mean and Median Survival Time
Example 4.1 on page 110. This uses the data set raw_data1 created in Section 4.1 for the survival function estimate.
proc sort data=raw_data1;
by descending time_mp ;
run;
data exm110;
set raw_data1 nobs = last;
lagt = lag(time_mp);
if _n_ = 1 then
med = surv*(35 - time_mp);
else med = surv*(lagt- time_mp); output;
if _n_ =last then do; med = 6; output; end;
run;
data exm110a;
set exm110 nobs=last;
retain sumd var35 0 ;
sumd = sumd + med;
var35 = var35 + ( sumd**2 ) * num_event/(num_left*(num_left-num_event));
if _n_ =last then var35=.;
run;
proc print data = exm110a noobs;
var time_mp sumd var35;
run;
time_mp sumd var35
23 5.3782 0.96415
22 5.9160 1.79745
16 9.6807 2.64941
13 11.7513 3.69556
10 14.0101 4.63024
7 16.4303 5.62272
6 17.2874 7.99457
6 23.2874 .
Example 4.2 on page 111. The first row of the table. The other two rows can be obtained in the same fashion. This example uses the data set table4_4 created in Section 4.3 for the survival function estimate. In the following example, we didn’t use Enfron’s tail correction.
proc sort data=table4_4; by descending t2; run; proc sql; select min(t2) into :mint from table4_4; quit; data exm111; set table4_4 nobs = last; lagt = lag(t2); if _n_ = 1 then med = surv*(2081 - t2); else med = surv*(lagt- t2); output; if _n_ =last then do; med = &mint; output; end; run; data exm111a; set exm111 nobs=last; retain sumd vmean 0 ; sumd = sumd + med; vmean = vmean + ( sumd**2 ) * num_event/(num_left*(num_left-num_event)); if _n_ =last then vmean=sqrt(vmean); run; data exm111b; set exm111a nobs=last; if _n_ =last then do; stderr = vmean; clow = sumd - 1.96*stderr; chigh = sumd + 1.96*stderr; end; if _n_ ~= last then delete; run; proc print data = exm111b noobs ; var sumd stderr clow chigh; run;
sumd stderr clow chigh 899.225 148.086 608.977 1189.47
Section 4.6 Estimators of the Survival Function for Left-Truncated and Right-Censored Data
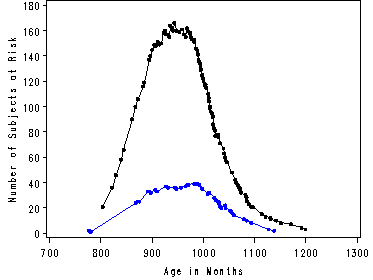
The following example is based on Channing House data which we created in a data step and called channing.
data c_male;
set channing;
cons = 1;
if gender = 1;
run;
proc phreg data=c_male noprint;
model (age_entry, age_death)*death(0)=cons;
output out=num_male num_left=num_left_male /method = pl;
run;
data c_female;
set channing;
cons = 1;
if gender = 2;
run;
proc phreg data=c_female noprint;
model (age_entry, age_death)*death(0)=cons;
output out=num_female num_left=num_left_female /method = pl;
run;
proc sort data=num_male;
by age_death;
proc sort data=num_female;
by age_death;
run;
data combined;
merge num_male (in=male) num_female (in = female);
by age_death;
run;
symbol1 i = join v = dot h = 0.5 c = black;
symbol2 i = join v = dot h = 0.5 c = blue;
axis1 order = (700 to 1300 by 100) minor = none;
axis2 order = (0 to 180 by 20) minor = none label = (a=90);
proc gplot data=combined;
plot num_left_female*age_death = 1 num_left_male*age_death = 2
/overlay haxis=axis1 vaxis=axis2;
label age_death = "Age in Months";
run;
quit;