Section 8.2: Partial Likelihood for Distinct-Event Time Data
Example 8.1 uses data set sec1_5 introduced in Section 1.5. This example is to illustrate the algorithm used to compute the parameter estimate. We simply use the SAS procedure PHREG to obtain the final result.
data example8_1; set sec1_5; group1 = group - 1; run; proc phreg data = example8_1; model time*death(0)=group1; run;
The PHREG Procedure
Model Information
Data Set WORK.EXAMPLE8_1
Dependent Variable time
Censoring Variable death
Censoring Value(s) 0
Ties Handling BRESLOW
Summary of the Number of Event and Censored Values
Percent
Total Event Censored Censored
45 24 21 46.67
Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 167.488 163.041
AIC 167.488 165.041
SBC 167.488 166.219
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 4.4463 1 0.0350
Score 5.4943 1 0.0191
Wald 5.0804 1 0.0242
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
group1 1 0.98022 0.43489 5.0804 0.0242 2.665
Section 8.3: Partial Likelihood When Ties Are Present
Example 8.2 uses data set kidney introduced in Section 1.4. The default to deal with ties in proc phreg is the Breslow’s method. Then we subsequently request for Efron’s and the discrete likelihood method.
data kidney1;
set kidney;
z1 = placement-1;
z2 = log(time)*z1;
run;
proc phreg data=kidney1 ;
model time*infect(0)= z1 /itprint;
run;
The PHREG Procedure
Model Information
Data Set WORK.KIDNEY1
Dependent Variable time
Censoring Variable infect
Censoring Value(s) 0
Ties Handling BRESLOW
Maximum Likelihood Iteration History
Iter Ridge Log Likelihood z1
0 0 -104.4533567733 0.000000000
1 0 -103.2287813714 -0.627539780
2 0 -103.2285047486 -0.618166307
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 2.4497 1 0.1175
Score 2.4873 1 0.1148
Wald 2.4108 1 0.1205
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
z1 1 -0.61817 0.39813 2.4108 0.1205 0.539
proc phreg data=kidney1;
model time*infect(0)= z1 /ties = efron itprint;
run;
The PHREG Procedure
Model Information
Data Set WORK.KIDNEY1
Dependent Variable time
Censoring Variable infect
Censoring Value(s) 0
Ties Handling EFRON
Maximum Likelihood Iteration History
Iter Ridge Log Likelihood z1
0 0 -104.2318524204 0.000000000
1 0 -103.0280587262 -0.621502286
2 0 -103.0278069637 -0.612565166
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 2.4081 1 0.1207
Score 2.4439 1 0.1180
Wald 2.3699 1 0.1237
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
z1 1 -0.61257 0.39791 2.3699 0.1237 0.542
proc phreg data=kidney1;
model time*infect(0)= z1 /ties = discrete itprint;
run;
The PHREG Procedure
Model Information
Data Set WORK.KIDNEY1
Dependent Variable time
Censoring Variable infect
Censoring Value(s) 0
Ties Handling DISCRETE
Maximum Likelihood Iteration History
Iter Ridge Log Likelihood z1
0 0 -94.18686530564 0.000000000
1 0 -92.94034563098 -0.638191845
2 0 -92.94010886461 -0.629438386
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 2.4935 1 0.1143
Score 2.5295 1 0.1117
Wald 2.4529 1 0.1173
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
z1 1 -0.62944 0.40190 2.4529 0.1173 0.533
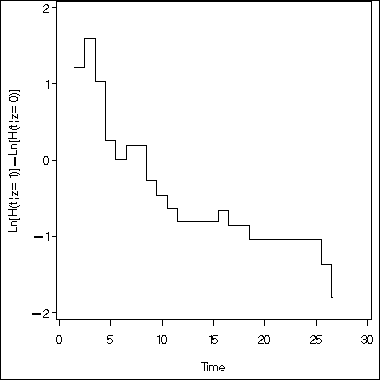
Figure 8.1 on graphical checking of the proportional hazards assumption for the renal insufficiency study. This uses the same data set as the above example.
proc phreg data = kidney1 ;
model time*infect(0) = ;
strata z1;
output out = fig8_1 (keep = time z1 logsurv) logsurv = logsurv /method=ch;
run;
proc sort data = fig8_1 nodup;
by time;
run;
proc transpose data = fig8_1 out = fig8_1f (drop = _name_ _label_) prefix = ls;
by time;
var logsurv;
run;
data fig8_1final;
set fig8_1f;
diff = log(-ls2) -log(-ls1);
where time >=1.5;
run;
goptions reset = all;
symbol i = stepjl;
axis1 order = (-2 to 2 by 1) label=(a=90 'Ln[H(t|z=1)]-Ln[H(t|z=0)]') minor=none;
axis2 order = (0 to 30 by 5) minor = none label=('Time');
proc gplot data= fig8_1final;
plot diff*time /overlay haxis=axis2 vaxis = axis1;
run;
quit;
Example 8.3 on page 242 uses a data set described in Section 1.8. We have created this data set here.
data example8_3;
set sec1_8;
array z(4);
do i = 1 to 4;
z(i) = (stage = i);
end;
run;
proc phreg data = example8_3;
model time*death(0) = z1 z2 z3;
run;
The PHREG Procedure
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 16.2634 3 0.0010
Score 22.4550 3 <.0001
Wald 18.9456 3 0.0003
Section 8.4: Local Tests
Example 8.3 (continued) on page 245. The data set used is sec1_8. This is to show how to get Wald test, score test and likelihood ratio test using SAS. The test statement in the first proc phreg gives Wald test.
data example8_3;
set sec1_8;
array z(4);
do i = 1 to 4;
z(i) = (stage = i);
end;
run;
proc phreg data = example8_3;
model time*death(0) = age z1 z2 z3 ;
test z1, z2, z3;
run;
The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
age 1 0.01890 0.01425 1.7589 0.1848 1.019
z1 1 -1.69333 0.42218 16.0876 <.0001 0.184
z2 1 -1.55491 0.50406 9.5157 0.0020 0.211
z3 1 -1.05518 0.41064 6.6029 0.0102 0.348
Linear Hypotheses Testing Results
Wald
Label Chi-Square DF Pr > ChiSq
Test 1 17.6371 3 0.0005
To obtain score test, we can use stepwise option after the model statement. The score test is given as residual Chi-square test shown below.
proc phreg data = example8_3; model time*death(0) = age z1 z2 z3 / selection=stepwise include=1 details ; run;
The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
age 1 0.02318 0.01447 2.5656 0.1092 1.023
Analysis of Variables Not in the Model
Score
Variable Chi-Square Pr > ChiSq
z1 5.3413 0.0208
z2 0.7983 0.3716
z3 0.9372 0.3330
Residual Chi-Square Test
Chi-Square DF Pr > ChiSq
20.5766 3 0.0001
To obtain likelihood test, we need to obtain the likelihood for both the model with age as the only covariate and the model with age and dummy variables for stage as covariates. These can be obtained by running each model with proc phreg.
proc phreg data = example8_3 outest=all4 noprint; model time*death(0) = age z2 z3 z4 ; run; proc phreg data = example8_3 outest=age noprint; model time*death(0) = age ; run; proc sql; select -2*( age._lnlike_- all4._lnlike_ ) as lratio from all4, age; quit;
lratio -------- 15.45291
Example 8.3 (continued) on page 247. This example still uses the data set example8_3 as shown above. To get the confidence interval for the risk of death, we use the option risklimits after the model statement.
proc phreg data = example8_3; model time*death(0) = age z2 z3 z4 /risklimits; run;
The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard 95% Hazard Ratio
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio Confidence Limits
age 1 0.01890 0.01425 1.7589 0.1848 1.019 0.991 1.048
z2 1 0.13842 0.46232 0.0896 0.7646 1.148 0.464 2.842
z3 1 0.63815 0.35609 3.2116 0.0731 1.893 0.942 3.804
z4 1 1.69333 0.42218 16.0876 <.0001 5.438 2.377 12.438
We can use test statement to test on if the relative risk (in the middle paragraph) differs from one shown below.
proc phreg data = example8_3;
model time*death(0) = age z2 z3 z4 ;
test z3 -z2 = 0 ;
run;
The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
age 1 0.01890 0.01425 1.7589 0.1848 1.019
z2 1 0.13842 0.46232 0.0896 0.7646 1.148
z3 1 0.63815 0.35609 3.2116 0.0731 1.893
z4 1 1.69333 0.42218 16.0876 <.0001 5.438
Linear Hypotheses Testing Results
Wald
Label Chi-Square DF Pr > ChiSq
Test 1 1.2245 1 0.2685
Finally, we will test if adjusted for age of the patient, survival is the same for stage II, III and IV patients. This is to test if the coefficients for z2, z3 and z4 are the same. With the test statement in proc phreg, we obtain Wald test.
proc phreg data = example8_3; model time*death(0) = age z2 z3 z4 ; test z2 = z3 = z4 ; run;
The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
age 1 0.01890 0.01425 1.7589 0.1848 1.019
z2 1 0.13842 0.46232 0.0896 0.7646 1.148
z3 1 0.63815 0.35609 3.2116 0.0731 1.893
z4 1 1.69333 0.42218 16.0876 <.0001 5.438
Linear Hypotheses Testing Results
Wald
Label Chi-Square DF Pr > ChiSq
Test 1 10.7404 2 0.0047
To obtain the likelihood ratio test, we run two models and take the difference of their likelihood. The difference of 386.275 and 376.359 yields 9.916 to be the likelihood ratio chi-square.
proc phreg data = example8_3; model time*death(0) = age z2 z3 z4 ; run; data example8_3a; set example8_3; zstar = z2 + z3 + z4; run; proc phreg data = example8_3a; model time*death(0) = age zstar ; run;
The PHREG Procedure
Model Information
Data Set WORK.EXAMPLE8_3
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 394.426 376.359
AIC 394.426 384.359
SBC 394.426 392.007
Model Information
Data Set WORK.EXAMPLE8_3A
Model Fit Statistics
Without With
Criterion Covariates Covariates
-2 LOG L 394.426 386.275
AIC 394.426 390.275
SBC 394.426 394.099
Example 8.3 (continued) on page 249 on interactions. Table 8.2 on page 250.
data table8_2; set example8_3; z5 = z2*age; z6 = z3*age; z7 = z4*age; run; proc phreg data = table8_2; model time*death(0) = age z2-z7; run;
The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
age 1 -0.00256 0.02605 0.0096 0.9218 0.997
z2 1 -7.94614 3.67821 4.6670 0.0307 0.000
z3 1 -0.12250 2.46833 0.0025 0.9604 0.885
z4 1 0.84702 2.42571 0.1219 0.7270 2.333
z5 1 0.12025 0.05231 5.2853 0.0215 1.128
z6 1 0.01135 0.03745 0.0919 0.7618 1.011
z7 1 0.01367 0.03597 0.1445 0.7038 1.014
Table 8.3 on page 251 and the tests in the paragraph.
proc phreg data = table8_2; model time*death(0) = age z2-z5; test_60: test 60*z5+z2=0; test_76: test 76*z5+z2=0; run;
The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
age 1 0.00597 0.01488 0.1610 0.6882 1.006
z2 1 -7.38147 3.40279 4.7056 0.0301 0.001
z3 1 0.62156 0.35581 3.0516 0.0807 1.862
z4 1 1.75350 0.42394 17.1084 <.0001 5.775
z5 1 0.11166 0.04767 5.4855 0.0192 1.118
Linear Hypotheses Testing Results
Wald
Label Chi-Square DF Pr > ChiSq
test_60 0.9686 1 0.3250
test_76 4.2899 1 0.0383
Section 8.5: Model Building Using the Proportional Hazards Model
Example 8.4 using the data set bone_marrow introduced in Section 1.3 with Table 8.4, Table 8.5, Table 8.6 and Table 8.7. We first create a couple of variables for the example and assign value labels for some of the variables.
data bone_marrow1;
set bone_marrow;
format g gs.
death dind.
relapse rind.
dfree dfs.
a aind.
c cind.
p pind.
z3 sex.
z4 sex.
z5 cmvs.
z6 cmvs.
z8 fab.
z10 yes.;
z1 = z1 - 28;
z2 = z2 - 28;
z1xz2 = z1 * z2;
label z1xz2 = "Age interaction";
g1 = ( g = 1 );
g2 = ( g = 2 );
g3 = ( g = 3 );
z3xz4 = z3*z4; /*interaction of sex*/
z5xz6 = z5*z6; /*interaction of cmv status*/
z1xz2 = z1*z2; /*interaction of age*/
run;
Now we are ready to produce these tables. Table 8.4 is created based on six runs of proc phreg. We use SAS 8 ODS feature here to collect all the AIC information in one data set and all the test statistic for each test in another data set and finally print them out. The ods listing close statement below stops the printing of the output in the output window until we issue statement ods listing near the end to turn it back on. This way, we will not see too much of the unnecessary output.
ods listing close;
proc phreg data = bone_marrow1;
model t2*dfree(0)= g2 g3 z7 ; /*waiting time is z7*/
z7: test z7 = 0;
ods output FitStatistics = z7aic;
ods output TestStmts = z7stat;
run;
proc phreg data = bone_marrow1;
model t2*dfree(0)= g2 g3 z8 ; /*fab is z8*/
z8: test z8 = 0;
ods output FitStatistics = z8aic;
ods output TestStmts = z8stat;
run;
proc phreg data = bone_marrow1;
model t2*dfree(0)= g2 g3 z10 ; /*MTX is z10*/
z10: test z10 = 0;
ods output FitStatistics = z10aic;
ods output TestStmts = z10stat;
run;
proc phreg data = bone_marrow1;
model t2*dfree(0)= g2 g3 z3 z4 z3xz4 ; /*SEX is z3 and z4*/
sex: test z3 = z4 = z3xz4 =0;
ods output FitStatistics = sexaic;
ods output TestStmts = sexstat;
run;
proc phreg data = bone_marrow1;
model t2*dfree(0)= g2 g3 z5 z6 z5xz6 ; /*CMV status is z5 and z6*/
cmv: test z5 = z6 = z5xz6 =0;
ods output FitStatistics = cmvaic;
ods output TestStmts = cmvstat;
run;
proc phreg data = bone_marrow1;
model t2*dfree(0)= g2 g3 z1 z2 z1xz2 ; /*age is z1 and z2*/
age: test z1 = z2 = z1xz2 =0;
ods output FitStatistics = ageaic;
ods output TestStmts = agestat;
run;
ods listing ;
data aic_table8_4;
set z7aic z8aic z10aic sexaic cmvaic ageaic;
run;
proc print data = aic_table8_4 noobs;
where criterion = "AIC";
var criterion withcovariates;
run;
data stat_table8_4;
set z7stat z8stat z10stat sexstat cmvstat agestat;
run;
proc print data = stat_table8_4 (drop=status) noobs;
run;
With
Criterion Covariates
AIC 737.947
AIC 731.020
AIC 737.348
AIC 741.440
AIC 743.105
AIC 733.181
Pro
Label WaldChiSq DF ChiSq
z7 1.1816 1 0.2770
z8 8.0815 1 0.0045
z1 2.0256 1 0.1547
se 1.9097 3 0.5914
cm 0.1861 3 0.9798
ag 11.9778 3 0.0075
Table 8.5 is done in the same way as above. We only show the program and the output.
ods listing close; proc phreg data = bone_marrow1; model t2*dfree(0)= g2 g3 z8 z7; z7: test z7 =0; ods output FitStatistics = z7aic_t5; ods output TestStmts = z7stat_t5; run; proc phreg data = bone_marrow1; model t2*dfree(0)= g2 g3 z8 z10 ; z10: test z10 =0; ods output FitStatistics = z10aic_t5; ods output TestStmts = z10stat_t5; run; proc phreg data = bone_marrow1; model t2*dfree(0)= g2 g3 z8 z3 z4 z3xz4 ; sex: test z3 = z4 = z3xz4 = 0; ods output FitStatistics = sexaic_t5; ods output TestStmts = sexstat_t5; run; proc phreg data = bone_marrow1; model t2*dfree(0)= g2 g3 z8 z5 z6 z5xz6 ; cmv: test z5 = z6 = z5xz6 = 0; ods output FitStatistics = cmvaic_t5; ods output TestStmts = cmvstat_t5; run; proc phreg data = bone_marrow1; model t2*dfree(0)= g2 g3 z8 z1 z2 z1xz2 ; age: test z1 = z2 = z1xz2 = 0; ods output FitStatistics = ageaic_t5; ods output TestStmts = agestat_t5; run; ods listing ; data aic_table8_5; set z7aic_t5 z10aic_t5 sexaic_t5 cmvaic_t5 ageaic_t5; run; proc print data = aic_table8_5 noobs; where criterion = "AIC"; var criterion withcovariates; run; data stat_table8_5; set z7stat_t5 z10stat_t5 sexstat_t5 cmvstat_t5 agestat_t5; run; proc print data = stat_table8_5 (drop=status) noobs; run;
With
Criterion Covariates
AIC 731.678
AIC 731.057
AIC 736.114
AIC 736.999
AIC 725.982
Prob
Label WaldChiSq DF ChiSq
z7 1.1811 1 0.2771
z1 2.0492 1 0.1523
se 0.9240 3 0.8196
cm 0.0218 3 0.9992
ag 13.0528 3 0.0045
Table 8.6 is also done in the same way.
ods listing close;
proc phreg data = bone_marrow1;
model t2*dfree(0)= g2 g3 z8 z1 z2 z1xz2 z7;
z7: test z7 = 0;
ods output FitStatistics = z7aic_t6;
ods output TestStmts = z7stat_t6;
run;
proc phreg data = bone_marrow1;
model t2*dfree(0)= g2 g3 z8 z1 z2 z1xz2 z10 ;
z10: test z10 = 0;
ods output FitStatistics = z10aic_t6;
ods output TestStmts = z10stat_t6;
run;
proc phreg data = bone_marrow1;
model t2*dfree(0)= g2 g3 z8 z1 z2 z1xz2 z3 z4 z3xz4 ;
sex: test z3 = z4 = z3xz4 = 0;
ods output FitStatistics = sexaic_t6;
ods output TestStmts = sexstat_t6;
run;
proc phreg data = bone_marrow1;
model t2*dfree(0)= g2 g3 z8 z1 z2 z1xz2 z5 z6 z5xz6;
cmv: test z5 = z6 = z5xz6 = 0;
ods output FitStatistics = cmvaic_t6;
ods output TestStmts = cmvstat_t6;
run;
ods listing ;
data aic_table8_6;
set z7aic_t6 z10aic_t6 sexaic_t6 cmvaic_t6 ;
run;
proc print data = aic_table8_6 noobs;
where criterion = "AIC";
var criterion withcovariates;
run;
data stat_table8_6;
set z7stat_t6 z10stat_t6 sexstat_t6 cmvstat_t6;
run;
proc print data = stat_table8_6 (drop=status) noobs;
run;
With
Criterion Covariates
AIC 727.480
AIC 726.580
AIC 730.610
AIC 731.420
Prob
Label WaldChiSq DF ChiSq
z7 0.4648 1 0.4954
z1 1.4438 1 0.2295
se 1.3675 3 0.7132
cm 0.5772 3 0.9016
Table 8.7 on page 256.
proc phreg data = bone_marrow1;
model t2*dfree(0)= g2 g3 z8 z1 z2 z1xz2 ;
run;
The PHREG Procedure
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio Variable Label
g2 1 -1.09058 0.35430 9.4752 0.0021 0.336
g3 1 -0.40439 0.36278 1.2425 0.2650 0.667
z8 1 0.83687 0.27853 9.0276 0.0027 2.309 FAB
z1 1 0.00686 0.01968 0.1214 0.7276 1.007 Patient Age
z2 1 0.00391 0.01826 0.0458 0.8305 1.004 Donor Age
z1xz2 1 0.00315 0.0009498 11.0074 0.0009 1.003 Age interaction
Example 8.5 is based on the data set described in Section 1.14. We have created a data set for it called sec1_14. We first create necessary dummy variables for the analysis in the example. The approach we use for creating the table is the same as the previous example.
data table8_8; set sec1_14; race1 = (race=1); race2 = (race=2); race3 = (race=3); edu1 = ( edu < 12); /*less than high school*/ edu2 = (edu = 12); /*high school graduate*/ edu3 = (edu > 12); /*some college*/ run;
Table 8.8 on page 257. Each row corresponds to a proc phreg. Notice we use ties = discrete option here because there are many ties in the data set.
proc phreg data = table8_8;
model duration*ind(0) = race1 race2 /ties=discrete;
race: test race1 = race2 = 0;
ods output FitStatistics = raceaic_t8;
ods output TestStmts = racestat_t8;
run;
proc phreg data = table8_8;
model duration*ind(0) = poverty /ties=discrete;
poverty: test poverty = 0;
ods output FitStatistics = povaic_t8;
ods output TestStmts = povstat_t8;
run;
proc phreg data = table8_8;
model duration*ind(0) = smoke /ties=discrete;
smoke: test smoke = 0;
ods output FitStatistics = smokeaic_t8;
ods output TestStmts = smokestat_t8;
run;
proc phreg data = table8_8;
model duration*ind(0) = alcohol /ties=discrete;
alcohol: test alcohol = 0;
ods output FitStatistics = alaic_t8;
ods output TestStmts = alstat_t8;
run;
proc phreg data = table8_8;
model duration*ind(0) = age /ties=discrete;
age: test age = 0;
ods output FitStatistics = ageaic_t8;
ods output TestStmts = agestat_t8;
run;
proc phreg data = table8_8;
model duration*ind(0) = edu1 edu2 /ties=discrete;
edu: test edu1 = edu2 = 0;
ods output FitStatistics = eduaic_t8;
ods output TestStmts = edustat_t8;
run;
proc phreg data = table8_8;
model duration*ind(0) = pcare /ties=discrete;
pcare: test pcare = 0;
ods output FitStatistics = pcareaic_t8;
ods output TestStmts = pcarestat_t8;
run;
ods listing ;
data aic_table8_8;
set raceaic_t8 povaic_t8 smokeaic_t8 alaic_t8 ageaic_t8 eduaic_t8 pcareaic_t8;
run;
proc print data = aic_table8_8 noobs;
where criterion = "AIC";
var criterion withcovariates;
run;
data stat_table8_8;
set racestat_t8 povstat_t8 smokestat_t8 alstat_t8 agestat_t8 edustat_t8 pcarestat_t8;
run;
proc print data = stat_table8_8 (drop=status) noobs;
run;
Criterion Covariates
AIC 5481.666
AIC 5486.689
AIC 5477.610
AIC 5485.479
AIC 5487.260
AIC 5482.364
AIC 5487.250
Prob
Label WaldChiSq DF ChiSq
race 8.0347 2 0.0180
pove 0.7127 1 0.3985
smok 10.0540 1 0.0015
alco 2.0064 1 0.1566
age 0.1500 1 0.6986
edu 6.9460 2 0.0310
pcar 0.1652 1 0.6844
Table 8.9 on page 257, similar with Table 8.8, adjusting for mother's smoking status.
ods listing close;
proc phreg data = table8_8;
model duration*ind(0) = smoke race1 race2 /ties=discrete;
race: test race1=race2=0;
ods output FitStatistics = raceaic_t9;
ods output TestStmts = racestat_t9;
run;
proc phreg data = table8_8;
model duration*ind(0) = smoke poverty /ties=discrete;
poverty: test poverty = 0;
ods output FitStatistics = povaic_t9;
ods output TestStmts = povstat_t9;
run;
proc phreg data = table8_8;
model duration*ind(0) = smoke alcohol /ties=discrete;
alcohol: test alcohol = 0;
ods output FitStatistics = alaic_t9;
ods output TestStmts = alstat_t9;
run;
proc phreg data = table8_8;
model duration*ind(0) = smoke age /ties=discrete;
age: test age = 0;
ods output FitStatistics = ageaic_t9;
ods output TestStmts = agestat_t9;
run;
proc phreg data = table8_8;
model duration*ind(0) = smoke edu1 edu2 /ties=discrete;
edu: test edu1 = edu2 = 0;
ods output FitStatistics = eduaic_t9;
ods output TestStmts = edustat_t9;
run;
proc phreg data = table8_8;
model duration*ind(0) = smoke pcare /ties=discrete;
pcare: test pcare = 0;
ods output FitStatistics = pcareaic_t9;
ods output TestStmts = pcarestat_t9;
run;
ods listing;
data aic_table8_9;
set raceaic_t9 povaic_t9 alaic_t9 ageaic_t9 eduaic_t9 pcareaic_t9;
run;
proc print data = aic_table8_9 noobs;
where criterion = "AIC";
var criterion withcovariates;
run;
data stat_table8_9;
set racestat_t9 povstat_t9 alstat_t9 agestat_t9 edustat_t9 pcarestat_t9;
run;
proc print data = stat_table8_9 (drop=status) noobs;
run;
With
Criterion Covariates
AIC 5469.708
AIC 5478.169
AIC 5478.594
AIC 5479.607
AIC 5477.706
AIC 5479.591
Prob
Label WaldChiSq DF ChiSq
race 12.3799 2 0.0020
pove 1.4170 1 0.2339
alco 1.0444 1 0.3068
age 0.0033 1 0.9544
edu 3.8660 2 0.1447
pcar 0.0199 1 0.8877
Table 8.10 on page 258.
ods listing close;
proc phreg data = table8_8;
model duration*ind(0) = smoke race1 race2 poverty /ties=discrete;
poverty: test poverty;
ods output FitStatistics = povaic_t10;
ods output TestStmts = povstat_t10;
run;
proc phreg data = table8_8;
model duration*ind(0) = smoke race1 race2 alcohol /ties=discrete;
alcohol: test alcohol = 0;
ods output FitStatistics = alaic_t10;
ods output TestStmts = alstat_t10;
run;
proc phreg data = table8_8;
model duration*ind(0) = smoke race1 race2 age /ties=discrete;
age: test age = 0;
ods output FitStatistics = ageaic_t10;
ods output TestStmts = agestat_t10;
run;
proc phreg data = table8_8;
model duration*ind(0) = smoke race1 race2 edu1 edu2 /ties=discrete;
edu: test edu1 = edu2 = 0;
ods output FitStatistics = eduaic_t10;
ods output TestStmts = edustat_t10;
run;
proc phreg data = table8_8;
model duration*ind(0) = smoke race1 race2 pcare /ties=discrete;
pcare: test pcare = 0;
ods output FitStatistics = pcareaic_t10;
ods output TestStmts = pcarestat_t10;
run;
ods listing;
data aic_table8_10;
set povaic_t10 alaic_t10 ageaic_t10 eduaic_t10 pcareaic_t10;
run;
proc print data = aic_table8_10 noobs;
where criterion = "AIC";
var criterion withcovariates;
run;
data stat_table8_10;
set povstat_t10 alstat_t10 agestat_t10 edustat_t10 pcarestat_t10;
run;
proc print data = stat_table8_10 (drop=status) noobs;
run;
With
Criterion Covariates
AIC 5468.648
AIC 5470.578
AIC 5471.514
AIC 5471.604
AIC 5471.674
Prob
Label WaldChiSq DF ChiSq
poverty 2.9879 1 0.0839
alcohol 1.1623 1 0.2810
age 0.1936 1 0.6599
edu 2.0801 2 0.3534
pcare 0.0339 1 0.8540
Table 8.11A and 8.11B on page 258.
proc phreg data = table8_8;
model duration*ind(0) = smoke race2 race3 /ties=discrete;
run;
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
smoke 1 0.30824 0.08139 14.3436 0.0002 1.361
race2 1 0.15574 0.11069 1.9797 0.1594 1.169
race3 1 0.35003 0.10208 11.7578 0.0006 1.419
proc phreg data = table8_8;
model duration*ind(0) = smoke race2 race3 poverty /ties=discrete;
run;
Analysis of Maximum Likelihood Estimates
Parameter Standard Hazard
Variable DF Estimate Error Chi-Square Pr > ChiSq Ratio
smoke 1 0.32814 0.08215 15.9568 <.0001 1.388
race2 1 0.18370 0.11183 2.6984 0.1004 1.202
race3 1 0.37367 0.10293 13.1794 0.0003 1.453
poverty 1 -0.16327 0.09445 2.9879 0.0839 0.849
Section 8.6: Estimation of the Survival Function
Example 8.3 (continued) on page 260. We make use the feature of the option covariates = data_set to estimate the survival function for 60-year old patient at different stage.
data age60;
input age z2 z3 z4;
cards;
60 0 0 0
60 1 0 0
60 0 1 0
60 0 0 1
;
run;
proc phreg data = example8_3;
model time*death(0) = age z2 z3 z4 ;
baseline out = surv60 survival = survival lower = slower upper = supper
covariates = age60 /method = ch nomean cltype = loglog ;
run;
proc print data = surv60 noobs;
where time = 5;
run;
age z2 z3 z4 time survival slower supper
60 0 0 0 5 0.70303 0.53187 0.82149
60 1 0 0 5 0.66720 0.41764 0.82899
60 0 1 0 5 0.51325 0.31714 0.67883
60 0 0 1 5 0.14721 0.02176 0.38329
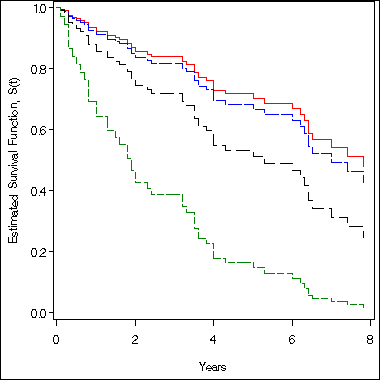
Figure 8.2 on page 261. We need to do a little bit of reshaping of the data before we can use the data to plot.
proc sort data= surv60;
by time;
run;
proc transpose data = surv60 out = fig8_2 (drop=_name_ _label_) prefix = s;
by time;
var survival;
run;
symbol1 i = stepjl l = 1 c=red ;
symbol2 i = stepjl l = 4 c=blue ;
symbol3 i = stepjl l = 21 c=black ;
symbol4 i = stepjl l = 29 c=green ;
axis1 order = (0 to 1 by .2) label=(a= 90 'Estimated Survival Function, S(t)') minor = none;
axis2 order = (0 to 8 by 2) label = ('Years') minor = none;
proc gplot data = fig8_2;
plot s1*time s2*time s3*time s4*time /overlay vaxis = axis1 haxis = axis2;
run;
quit;