Introduction
A typical use of a logarithmic transformation variable is to pull outlying data from a positively skewed distribution closer to the bulk of the data in a quest to have the variable be normally distributed. In regression analysis the logs of variables are routinely taken, not necessarily for achieving a normal distribution of the predictors and/or the dependent variable but for interpretability. The standard interpretation of coefficients in a regression analysis is that a one unit change in the independent variable results in the respective regression coefficient change in the expected value of the dependent variable while all the predictors are held constant. Interpreting a log transformed variable can be done in such a manner; however, such coefficients are routinely interpreted in terms of percent change (see Introductory Econometrics: A Modern Approach by Woolridge for discussion and derivation). Throughout this page we’ll explore the interpretation in a simple linear regression setting with either the dependent variable, independent variable, or both variables are log-transformed. We’ll use the hospital-level data from the Study on the Efficacy of Nosocomial Infection Control (data came from Applied Linear Regression Models 5th edition) where we’ll explore the relationship between average length of stay (in days) for all patients in the hospital (length) and the average daily number of patients in the hospital (census). The focus of this page is model interpretation, not model logistics.
NOTE: The ensuing interpretation is applicable for only log base e (natural log) transformations.
data senic; input id length age risk culture xray beds msch region census nurses svcs; datalines; 1 7.13 55.7 4.1 9.0 39.6 279 2 4 207 241 60.0 2 8.82 58.2 1.6 3.8 51.7 80 2 2 51 52 40.0 3 8.34 56.9 2.7 8.1 74.0 107 2 3 82 54 20.0 4 8.95 53.7 5.6 18.9 122.8 147 2 4 53 148 40.0 5 11.20 56.5 5.7 34.5 88.9 180 2 1 134 151 40.0 6 9.76 50.9 5.1 21.9 97.0 150 2 2 147 106 40.0 7 9.68 57.8 4.6 16.7 79.0 186 2 3 151 129 40.0 8 11.18 45.7 5.4 60.5 85.8 640 1 2 399 360 60.0 9 8.67 48.2 4.3 24.4 90.8 182 2 3 130 118 40.0 10 8.84 56.3 6.3 29.6 82.6 85 2 1 59 66 40.0 11 11.07 53.2 4.9 28.5 122.0 768 1 1 591 656 80.0 12 8.30 57.2 4.3 6.8 83.8 167 2 3 105 59 40.0 13 12.78 56.8 7.7 46.0 116.9 322 1 1 252 349 57.1 14 7.58 56.7 3.7 20.8 88.0 97 2 2 59 79 37.1 15 9.00 56.3 4.2 14.6 76.4 72 2 3 61 38 17.1 16 11.08 50.2 5.5 18.6 63.6 387 2 3 326 405 57.1 17 8.28 48.1 4.5 26.0 101.8 108 2 4 84 73 37.1 18 11.62 53.9 6.4 25.5 99.2 133 2 1 113 101 37.1 19 9.06 52.8 4.2 6.9 75.9 134 2 2 103 125 37.1 20 9.35 53.8 4.1 15.9 80.9 833 2 3 547 519 77.1 21 7.53 42.0 4.2 23.1 98.9 95 2 4 47 49 17.1 22 10.24 49.0 4.8 36.3 112.6 195 2 2 163 170 37.1 23 9.78 52.3 5.0 17.6 95.9 270 1 1 240 198 57.1 24 9.84 62.2 4.8 12.0 82.3 600 2 3 468 497 57.1 25 9.20 52.2 4.0 17.5 71.1 298 1 4 244 236 57.1 26 8.28 49.5 3.9 12.0 113.1 546 1 2 413 436 57.1 27 9.31 47.2 4.5 30.2 101.3 170 2 1 124 173 37.1 28 8.19 52.1 3.2 10.8 59.2 176 2 1 156 88 37.1 29 11.65 54.5 4.4 18.6 96.1 248 2 1 217 189 37.1 30 9.89 50.5 4.9 17.7 103.6 167 2 2 113 106 37.1 31 11.03 49.9 5.0 19.7 102.1 318 2 1 270 335 57.1 32 9.84 53.0 5.2 17.7 72.6 210 2 2 200 239 54.3 33 11.77 54.1 5.3 17.3 56.0 196 2 1 164 165 34.3 34 13.59 54.0 6.1 24.2 111.7 312 2 1 258 169 54.3 35 9.74 54.4 6.3 11.4 76.1 221 2 2 170 172 54.3 36 10.33 55.8 5.0 21.2 104.3 266 2 1 181 149 54.3 37 9.97 58.2 2.8 16.5 76.5 90 2 2 69 42 34.3 38 7.84 49.1 4.6 7.1 87.9 60 2 3 50 45 34.3 39 10.47 53.2 4.1 5.7 69.1 196 2 2 168 153 54.3 40 8.16 60.9 1.3 1.9 58.0 73 2 3 49 21 14.3 41 8.48 51.1 3.7 12.1 92.8 166 2 3 145 118 34.3 42 10.72 53.8 4.7 23.2 94.1 113 2 3 90 107 34.3 43 11.20 45.0 3.0 7.0 78.9 130 2 3 95 56 34.3 44 10.12 51.7 5.6 14.9 79.1 362 1 3 313 264 54.3 45 8.37 50.7 5.5 15.1 84.8 115 2 2 96 88 34.3 46 10.16 54.2 4.6 8.4 51.5 831 1 4 581 629 74.3 47 19.56 59.9 6.5 17.2 113.7 306 2 1 273 172 51.4 48 10.90 57.2 5.5 10.6 71.9 593 2 2 446 211 51.4 49 7.67 51.7 1.8 2.5 40.4 106 2 3 93 35 11.4 50 8.88 51.5 4.2 10.1 86.9 305 2 3 238 197 51.4 51 11.48 57.6 5.6 20.3 82.0 252 2 1 207 251 51.4 52 9.23 51.6 4.3 11.6 42.6 620 2 2 413 420 71.4 53 11.41 61.1 7.6 16.6 97.9 535 2 3 330 273 51.4 54 12.07 43.7 7.8 52.4 105.3 157 2 2 115 76 31.4 55 8.63 54.0 3.1 8.4 56.2 76 2 1 39 44 31.4 56 11.15 56.5 3.9 7.7 73.9 281 2 1 217 199 51.4 57 7.14 59.0 3.7 2.6 75.8 70 2 4 37 35 31.4 58 7.65 47.1 4.3 16.4 65.7 318 2 4 265 314 51.4 59 10.73 50.6 3.9 19.3 101.0 445 1 2 374 345 51.4 60 11.46 56.9 4.5 15.6 97.7 191 2 3 153 132 31.4 61 10.42 58.0 3.4 8.0 59.0 119 2 1 67 64 31.4 62 11.18 51.0 5.7 18.8 55.9 595 1 2 546 392 68.6 63 7.93 64.1 5.4 7.5 98.1 68 2 4 42 49 28.6 64 9.66 52.1 4.4 9.9 98.3 83 2 2 66 95 28.6 65 7.78 45.5 5.0 20.9 71.6 489 2 3 391 329 48.6 66 9.42 50.6 4.3 24.8 62.8 508 2 1 421 528 48.6 67 10.02 49.5 4.4 8.3 93.0 265 2 2 191 202 48.6 68 8.58 55.0 3.7 7.4 95.9 304 2 3 248 218 48.6 69 9.61 52.4 4.5 6.9 87.2 487 2 3 404 220 48.6 70 8.03 54.2 3.5 24.3 87.3 97 2 1 65 55 28.6 71 7.39 51.0 4.2 14.6 88.4 72 2 2 38 67 28.6 72 7.08 52.0 2.0 12.3 56.4 87 2 3 52 57 28.6 73 9.53 51.5 5.2 15.0 65.7 298 2 3 241 193 48.6 74 10.05 52.0 4.5 36.7 87.5 184 1 1 144 151 68.6 75 8.45 38.8 3.4 12.9 85.0 235 2 2 143 124 48.6 76 6.70 48.6 4.5 13.0 80.8 76 2 4 51 79 28.6 77 8.90 49.7 2.9 12.7 86.9 52 2 1 37 35 28.6 78 10.23 53.2 4.9 9.9 77.9 752 1 2 595 446 68.6 79 8.88 55.8 4.4 14.1 76.8 237 2 2 165 182 48.6 80 10.30 59.6 5.1 27.8 88.9 175 2 2 113 73 45.7 81 10.79 44.2 2.9 2.6 56.6 461 1 2 320 196 65.7 82 7.94 49.5 3.5 6.2 92.3 195 2 2 139 116 45.7 83 7.63 52.1 5.5 11.6 61.1 197 2 4 109 110 45.7 84 8.77 54.5 4.7 5.2 47.0 143 2 4 85 87 25.7 85 8.09 56.9 1.7 7.6 56.9 92 2 3 61 61 45.7 86 9.05 51.2 4.1 20.5 79.8 195 2 3 127 112 45.7 87 7.91 52.8 2.9 11.9 79.5 477 2 3 349 188 65.7 88 10.39 54.6 4.3 14.0 88.3 353 2 2 223 200 65.7 89 9.36 54.1 4.8 18.3 90.6 165 2 1 127 158 45.7 90 11.41 50.4 5.8 23.8 73.0 424 1 3 359 335 45.7 91 8.86 51.3 2.9 9.5 87.5 100 2 3 65 53 25.7 92 8.93 56.0 2.0 6.2 72.5 95 2 3 59 56 25.7 93 8.92 53.9 1.3 2.2 79.5 56 2 2 40 14 5.7 94 8.15 54.9 5.3 12.3 79.8 99 2 4 55 71 25.7 95 9.77 50.2 5.3 15.7 89.7 154 2 2 123 148 25.7 96 8.54 56.1 2.5 27.0 82.5 98 2 1 57 75 45.7 97 8.66 52.8 3.8 6.8 69.5 246 2 3 178 177 45.7 98 12.01 52.8 4.8 10.8 96.9 298 2 1 237 115 45.7 99 7.95 51.8 2.3 4.6 54.9 163 2 3 128 93 42.9 100 10.15 51.9 6.2 16.4 59.2 568 1 3 452 371 62.9 101 9.76 53.2 2.6 6.9 80.1 64 2 4 47 55 22.9 102 9.89 45.2 4.3 11.8 108.7 190 2 1 141 112 42.9 103 7.14 57.6 2.7 13.1 92.6 92 2 4 40 50 22.9 104 13.95 65.9 6.6 15.6 133.5 356 2 1 308 182 62.9 105 9.44 52.5 4.5 10.9 58.5 297 2 3 230 263 42.9 106 10.80 63.9 2.9 1.6 57.4 130 2 3 69 62 22.9 107 7.14 51.7 1.4 4.1 45.7 115 2 3 90 19 22.9 108 8.02 55.0 2.1 3.8 46.5 91 2 2 44 32 22.9 109 11.80 53.8 5.7 9.1 116.9 571 1 2 441 469 62.9 110 9.50 49.3 5.8 42.0 70.9 98 2 3 68 46 22.9 111 7.70 56.9 4.4 12.2 67.9 129 2 4 85 136 62.9 112 17.94 56.2 5.9 26.4 91.8 835 1 1 791 407 62.9 113 9.41 59.5 3.1 20.6 91.7 29 2 3 20 22 22.9 ; run;
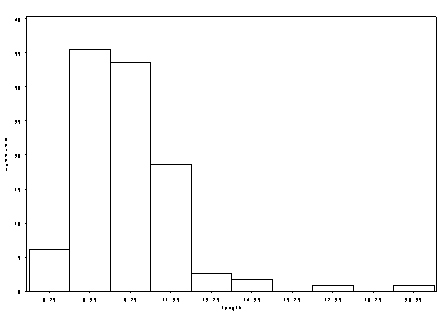
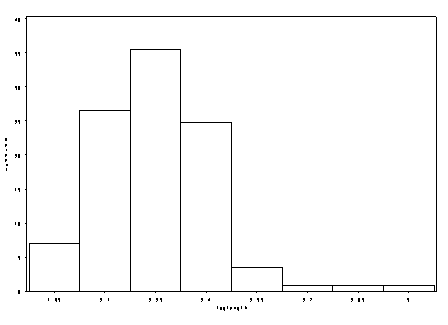
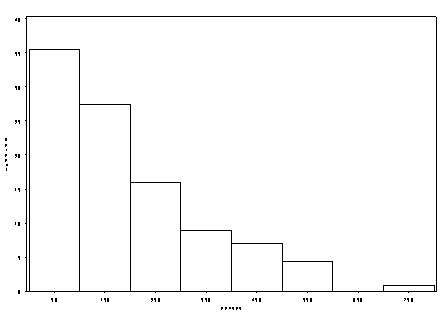
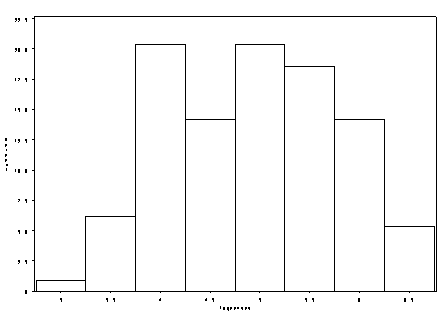
We’ll start of by looking at histograms of the length and census variable in its original metric and log-transformed state.
data senic; set senic; loglength = log(length); logcensus = log(census); run;proc univariate data = senic ; var length loglength census logcensus; histogram; run;
[univariate statistics omitted]
In both graphs, we saw how taking a log-transformation of the variable brought the outlying data points from the right tail towards the rest of the data. We’ll start off by interpreting a linear regression model where the variables are in their original metric and then proceed to include the variables in their transformed state.
Variables in their original metric
For the first model with the variables in their original state, we’ll regress average length of stay on the average daily number of patients in the hospital. The interpretation of the relationship is that a one person increase in the average daily number of patients in the hospital will change the average length of stay by 0.006 day.
proc reg data = senic; model length = census; run;The REG Procedure Model: MODEL1 Dependent Variable: lengthAnalysis of Variance Sum of Mean Source DF Squares Square F Value Pr > F Model 1 91.89534 91.89534 32.15 <.0001 Error 111 317.31504 2.85869 Corrected Total 112 409.21038 Root MSE 1.69077 R-Square 0.2246 Dependent Mean 9.64832 Adj R-Sq 0.2176 Coeff Var 17.52396 Parameter Estimates Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 8.52093 0.25463 33.46 <.0001 census 1 0.00589 0.00104 5.67 <.0001
Dependent variable transformed
In this model, the dependent variable is in its log-transformed state, and the independent variable is in its original metric. Comparing the coefficient for census to that obtained in the prior model, we note that there is a big difference in coefficients; however, we must recall the scale of the dependent variable changed states. In such models where the dependent variable has been log-transformed and the predictors have not. To interpet the amount of change in the original metric of the outcome, we first exponentiate the coefficient of census to obtain exp(0.00055773)=1.000558. To calculate the percent change, we can subtract one from this number and multiply by 100. Thus, for a one unit increase in the average daily number of patients (census), the average length of stay (length) increases by 0.06 percent.
proc reg data = senic; model loglength = census; run;The REG Procedure Model: MODEL1 Dependent Variable: loglength Analysis of Variance Sum of Mean Source DF Squares Square F Value Pr > F Model 1 0.82367 0.82367 33.57 <.0001 Error 111 2.72379 0.02454 Corrected Total 112 3.54745 Root MSE 0.15665 R-Square 0.2322 Dependent Mean 2.25012 Adj R-Sq 0.2253 Coeff Var 6.96177 Parameter Estimates Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 2.14339 0.02359 90.85 <.0001 census 1 0.00055773 0.00009627 5.79 <.0001
Independent variable transformed
In this model we are going to have the dependent variable in its original metric and the independent variable log-transformed. A comparison to the prior two models reveals that the regression coefficient is drastically different. Similar to the prior example the interpretation has a nice format, a one percent increase in the independent variable increases (or decreases) the dependent variable by (coefficient/100) units. In this particular model we’d say that a one percent increase in the average daily number of patients in the hospital would result in a (1.155/100) = 0.012 day increase in the average length of stay.
proc reg data = senic; model length = logcensus; run;The REG Procedure Model: MODEL1 Dependent Variable: length Analysis of Variance Sum of Mean Source DF Squares Square F Value Pr > F Model 1 97.87500 97.87500 34.90 <.0001 Error 111 311.33538 2.80482 Corrected Total 112 409.21038 Root MSE 1.67476 R-Square 0.2392 Dependent Mean 9.64832 Adj R-Sq 0.2323 Coeff Var 17.35806 Parameter Estimates Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 3.93711 0.97957 4.02 0.0001 logcensus 1 1.15513 0.19554 5.91 <.0001
Both dependent and independent variables transformed
In instances where both the dependent variable and independent variable(s) are log-transformed variables, the relationship is commonly referred to as elastic in econometrics. In a regression setting, we’d interpret the elasticity as the percent change in y (the dependent variable), while x (the independent variable) increases by one percent. For this model we’d conclude that a one percent increase in the average daily number of patients in the hospital would yield a 0.11% increase in the average length of stay.
proc reg data = senic; model loglength = logcensus; run;The REG Procedure Model: MODEL1 Dependent Variable: loglength Analysis of Variance Sum of Mean Source DF Squares Square F Value Pr > F Model 1 0.94180 0.94180 40.12 <.0001 Error 111 2.60566 0.02347 Corrected Total 112 3.54745 Root MSE 0.15321 R-Square 0.2655 Dependent Mean 2.25012 Adj R-Sq 0.2589 Coeff Var 6.80912 Parameter Estimates Parameter Standard Variable DF Estimate Error t Value Pr > |t| Intercept 1 1.68988 0.08961 18.86 <.0001 logcensus 1 0.11331 0.01789 6.33 <.0001