Attention
See this FAQ by Bauer that discusses the need to decompose within- and between-group effects when using this approach to ensure valid results (https://dbauer.web.unc.edu/wp-content/uploads/sites/7494/2015/08/Centering-in-111-Mediation.pdf).
FAQ starts here
Version info: Code for this page was tested in SAS 9.3.
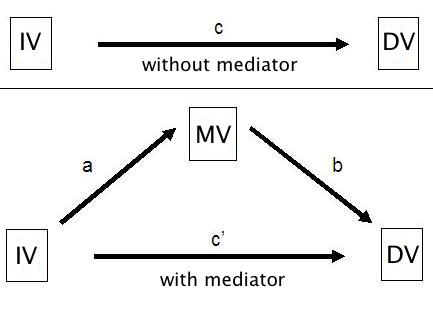
Mediator variables are variables that sit between the independent variable and dependent variable and mediate the effect of the IV on the DV. A model with one mediator is shown in the figure below.
The idea, in mediation analysis, is that some of the effect of the predictor variable, the IV, is transmitted to the DV through the mediator variable, the MV. And some of the effect of the IV passes directly to the DV. That portion of of the effect of the IV that passes through the MV is the indirect effect.
An earlier approach to multilevel mediation suggested by Krull & MacKinnon (2001) was method 1. This page will demonstrate an alternative approach given in the 2006 paper by Bauer, Preacher & Gil. This approach combines the dependent variable and the mediator into a single stacked response variable and runs one mixed model with indicator variables for the DV and mediator to obtain all of the values needed for the analysis.
We will begin by loading in a synthetic data set and reconfiguring it for our analysis. All of the variables in this example (id the cluster ID, x the predictor variable, m the mediator variable, and y the dependent variable) are at level 1 Here is how the first 16 observations look in the original dataset. Let’s start by reading in the data and looking at a few descriptive statistics.
filename tmp url 'http://stats.idre.ucla.edu/stat/data/ml_sim.csv'; data ml_sim; infile tmp dlm=',' firstobs=2; input id x m y; fid = _n_; run; proc means; var id fid x m y; run; The MEANS Procedure Variable N Mean Std Dev Minimum Maximum ------------------------------------------------------------------------------- id 800 50.5000000 28.8841283 1.0000000 100.0000000 fid 800 400.5000000 231.0844002 1.0000000 800.0000000 x 800 -0.1539876 1.3303736 -4.1514263 3.8696609 m 800 -0.0247739 1.4836143 -6.4783697 5.0124219 y 800 -0.1833981 1.6691804 -8.6000316 5.9190076 -------------------------------------------------------------------------------
There are 100 level-2 units each with eight observations. fid is a row id, so when the data is not stacked, there is just 1 obsevation for each fid. Let’s look at the three models of a mediation analysis beginning with the model with just the IV.
proc mixed noclprint;
class id;
model y = x / solution;
random intercept x / subject=id;
run;
Covariance Parameter Estimates
Cov Parm Subject Estimate
Intercept id 0.7505
x id 0.2192
Residual 0.8217
Fit Statistics
-2 Res Log Likelihood 2435.3
AIC (smaller is better) 2441.3
AICC (smaller is better) 2441.3
BIC (smaller is better) 2449.1
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept -0.02737 0.09620 99 -0.28 0.7766
x 0.6907 0.05883 99 11.74
Next, comes the model with the mediator predicted by the IV.
proc mixed noclprint;
class id;
model m = x / solution;
random intercept x / subject=id;
run;
Covariance Parameter Estimates
Cov Parm Subject Estimate
Intercept id 0.7087
x id 0.1165
Residual 0.6451
Fit Statistics
-2 Res Log Likelihood 2234.6
AIC (smaller is better) 2240.6
AICC (smaller is better) 2240.6
BIC (smaller is better) 2248.4
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept 0.09519 0.09158 99 1.04 0.3012
x 0.6114 0.04641 99 13.17
Finally, the model with both the IV and mediator predicting the DV.
proc mixed noclprint;
class id;
model y = m x / solution;
random intercept m x / subject=id;
run;
Covariance Parameter Estimates
Cov Parm Subject Estimate
Intercept id 0.2653
m id 0.1230
x id 0.03747
Residual 0.5070
Fit Statistics
-2 Res Log Likelihood 2046.8
AIC (smaller is better) 2054.8
AICC (smaller is better) 2054.9
BIC (smaller is better) 2065.3
Solution for Fixed Effects
Standard
Effect Estimate Error DF t Value Pr > |t|
Intercept -0.09364 0.06251 99 -1.50 0.1373
m 0.6219 0.04721 99 13.17
We see that the IV although still significant has been reduced from .69 to .25. Now, we need to restructure the data to stack y on m for each row and create indicator variables for both the mediator and the dependent variables. Here’s how we can do this.
data ml_simlong; set ml_sim; z = y; sy = 1; sm = 0; dv = 'y'; output; z = m; sy = 0; sm = 1; dv = 'm'; output; run;
The new response variable is called z and has y stacked on m. We named the indicators for the mediator and the DV sm and sy respectively, to be consistent with Bauer et al (2006). We have also created a new m that contains the value for the mediator from each of the original observations.
Now we can run our mixed model for multilevel mediation using proc mixed. Notice that because we include the sm and sy indicators in the model that we need to use the noint option for the fixed effects (it is not automatically included for random effects, so there is no need to supress it). In addition to the random effects, we use a repeated subcommand to model the heterogeneity in residual variances for y and m (which are now stacked and just in the variable z.
proc mixed data=ml_simlong noclprint covtest;
class id dv;
model z = sm sm * x sy sy * m sy * x /noint solution covb;
random sm sm * x sy sy * m sy * x / subject=id type=un;
repeated / group=dv subject=id;
run;
The Mixed Procedure
Model Information
Data Set WORK.ML_SIMLONG
Dependent Variable z
Covariance Structures Unstructured, Variance
Components
Subject Effects id, id
Group Effect dv
Estimation Method REML
Residual Variance Method None
Fixed Effects SE Method Model-Based
Degrees of Freedom Method Containment
Dimensions
Covariance Parameters 17
Columns in X 5
Columns in Z Per Subject 5
Subjects 100
Max Obs Per Subject 16
Number of Observations
Number of Observations Read 1600
Number of Observations Used 1600
Number of Observations Not Used 0
Iteration History
Iteration Evaluations -2 Res Log Like Criterion
0 1 5018.02760634
1 4 4324.76342851 50.66699378
2 3 4303.83578771 29.81384239
3 2 4284.51183182 26.06489084
4 1 4262.57000555 0.02711155
5 2 4253.92727615 0.00276758
6 2 4252.35296469 0.00012231
7 1 4252.26931686 0.00000042
8 1 4252.26903780 0.00000000
Convergence criteria met.
Covariance Parameter Estimates
Standard Z
Cov Parm Subject Group Estimate Error Value Pr Z
UN(1,1) id 0.6794 0.1132 6.00 0.09896 0.02282 4.34 ChiSq
16 765.76 |t|
sm 0.09321 0.08943 99 1.04 0.2998
sm*x 0.6119 0.04650 99 13.16 0.6106 0.04554 99 13.41 0.2208 0.03725 99 5.93 0.002162 0.000127 0.000985 -0.00020
3 sy 0.000576 0.000127 0.003839 -0.00011 -0.00006
4 sy*m 0.000093 0.000985 -0.00011 0.002074 -0.00048
5 x*sy -0.00006 -0.00020 -0.00006 -0.00048 0.001387
Type 3 Tests of Fixed Effects
Num Den
Effect DF DF F Value Pr > F
sm 1 99 1.09 0.2998
sm*x 1 99 173.17
We now have access to all of the information needed to compute the average indirect effect and average total effect and their standard errors using the equations given in Bauer, et. al. (2006).
[ ind = ab + sigma_{a_{j}b_{j}} quad (EQ:A11) ] [ Var(ind) = b^{2}sigma^{2}_{hat{a}} + a^{2}sigma^{2}_{hat{b}} + sigma^{2}_{hat{a}}sigma^{2}_{hat{b}} + 2absigma_{hat{a},hat{b}} + (sigma_{hat{a},hat{b}})^2 + sigma^{2}_{hat{sigma}_{a_{j},b_{j}}} quad (EQ:A14) ]
average total effect
[ tot = ab + sigma_{a_{j}b_{j}} + c’ quad (EQ:A15) ] [ Var(ind) = b^{2}sigma^{2}_{hat{a}} + a^{2}sigma^{2}_{hat{b}} + 2absigma_{hat{a},hat{b}} + 2bsigma_{hat{a},hat{c}’} + 2asigma_{hat{b},hat{c}’} + sigma^{2}_{hat{sigma}_{a_{j},b_{j}}} + sigma^{2}_{hat{c}’} + sigma^{2}_{hat{a}}sigma^{2}_{hat{b}} + (sigma_{hat{a},hat{b}})^2 quad (EQ:A18) ]
These formulae involve the fixed effects estimates, their variances and covariances, and variances and covariances from the random effects. The values used are highlighted in yellow in the SAS output above.
[ a = 0.6119 b = 0.6106 c’ = 0.2208 sigma_{a_{j}b_{j}} = 0.09896 sigma^{2}_{hat{a}} = 0.002162 sigma^{2}_{hat{b}} = 0.002074 sigma_{hat{a},hat{b}} = 0.000985 sigma_{hat{a},hat{c}’} = -0.00020 sigma_{hat{b},hat{c}’} = -0.00048 sigma^{2}_{hat{c}’} = 0.001387 sigma^{2}_{hat{sigma}_{a_{j},b_{j}}} = 0.02282^{2} ]
To calculate this, you just need a calculator. A simple way in SAS is using SAS’ matrix language, in PROC IML, which essentially allows us to just declare the constants and write out the formulae.
proc iml; a = 0.6119; b = 0.6106; rcov_ab = 0.09896; cprime = 0.2208; Va = 0.002162; Vb = 0.002074; Vcprime = 0.001387; cov_ab = 0.000985; cov_ac = -0.00020; cov_bc = -0.00048; Vcov_ab = 0.022822**2; ind_eff = a*b + rcov_ab; V_ind_eff = a**2*Vb + b**2*Va + Va*Vb + 2*a*b*cov_ab + cov_ab**2 + Vcov_ab; test_ind = ind_eff/V_ind_eff**.5; tot_eff = ind_eff + cprime; V_tot_eff = b**2*Va + a**2*Vb + Va*Vb + 2*a*b*cov_ab + cov_ab**2 + Vcprime + 2*b*cov_ac + 2*a*cov_bc + Vcov_ab; test_tot = tot_eff/V_tot_eff**.5; print ind_eff; /* indirect effect */ print V_ind_eff; /* variance of indirect effect */ print test_ind; /* significance test of indirect effect, test against standard normal */ print tot_eff; /* total effect */ print V_tot_eff; /* variance of total effect */ print test_tot; /* significance test of total effect, test against standard normal */ quit; ind_eff 0.4725861 V_ind_eff 0.002845 test_ind 8.8601944 tot_eff 0.6933861 V_tot_eff 0.0034003 test_tot 11.890965
We get the indirect effect, the variance of the indirect effect, and a test value (the effect divided by its standard error), which we could calculate a p-value for by comparing it against the standard normal distribution. For anything greater than roughly 1.96 will be statistically significant at p = .05.
See also
If you do not want to calculate this all out by hand, you can go to Daniel Bauer’s website, where he has posted a PDF of the publication this page is based on as well as his own examples, and a SAS macro to calculate and test the indirect effects.
References
- Bauer, D. J., Preacher, K. J. & Gil, K. M. (2006) Conceptualizing and testing random indirect effects and moderated mediation in multilevel models: New procedures and recommendations. Psychological Methods, 11(2), 142-163.
- Krull, J. L. & MacKinnon, D. P. (2001) Multilevel modeling of individual and group level mediated effects. Multivariate Behavioral Research, 36(2), 249-277.