1. Introduction
This module illustrates some of the features of The SAS System. SAS is a comprehensive package with very powerful data management tools, a wide variety of statistical analysis and graphical procedures. This is a very brief introduction and only covers just a fraction of all of the features of SAS. We use the following data file to illustrate the features of SAS. This data file contains information about 26 automobiles, namely their make, price, miles per gallon, repair rating (in 1978), weight in pounds, length in inches, and whether the car was foreign or domestic. Here is the data file.
make price mpg rep78 weight length foreign AMC 4099 22 3 2930 186 0 AMC 4749 17 3 3350 173 0 AMC 3799 22 3 2640 168 0 Audi 9690 17 5 2830 189 1 Audi 6295 23 3 2070 174 1 BMW 9735 25 4 2650 177 1 Buick 4816 20 3 3250 196 0 Buick 7827 15 4 4080 222 0 Buick 5788 18 3 3670 218 0 Buick 4453 26 3 2230 170 0 Buick 5189 20 3 3280 200 0 Buick 10372 16 3 3880 207 0 Buick 4082 19 3 3400 200 0 Cad. 11385 14 3 4330 221 0 Cad. 14500 14 2 3900 204 0 Cad. 15906 21 3 4290 204 0 Chev. 3299 29 3 2110 163 0 Chev. 5705 16 4 3690 212 0 Chev. 4504 22 3 3180 193 0 Chev. 5104 22 2 3220 200 0 Chev. 3667 24 2 2750 179 0 Chev. 3955 19 3 3430 197 0 Datsun 6229 23 4 2370 170 1 Datsun 4589 35 5 2020 165 1 Datsun 5079 24 4 2280 170 1 Datsun 8129 21 4 2750 184 1
The program below reads the data and creates a temporary data file called auto. The descriptive statistics shown in this module are all performed on this data file called auto.
DATA auto ; INPUT make $ price mpg rep78 weight length foreign ; DATALINES; AMC 4099 22 3 2930 186 0 AMC 4749 17 3 3350 173 0 AMC 3799 22 3 2640 168 0 Audi 9690 17 5 2830 189 1 Audi 6295 23 3 2070 174 1 BMW 9735 25 4 2650 177 1 Buick 4816 20 3 3250 196 0 Buick 7827 15 4 4080 222 0 Buick 5788 18 3 3670 218 0 Buick 4453 26 3 2230 170 0 Buick 5189 20 3 3280 200 0 Buick 10372 16 3 3880 207 0 Buick 4082 19 3 3400 200 0 Cad. 11385 14 3 4330 221 0 Cad. 14500 14 2 3900 204 0 Cad. 15906 21 3 4290 204 0 Chev. 3299 29 3 2110 163 0 Chev. 5705 16 4 3690 212 0 Chev. 4504 22 3 3180 193 0 Chev. 5104 22 2 3220 200 0 Chev. 3667 24 2 2750 179 0 Chev. 3955 19 3 3430 197 0 Datsun 6229 23 4 2370 170 1 Datsun 4589 35 5 2020 165 1 Datsun 5079 24 4 2280 170 1 Datsun 8129 21 4 2750 184 1 ; RUN; PROC PRINT DATA=auto(obs=10); RUN;
The output of the proc print is shown below. You can compare the program to the output below.
OBS MAKE PRICE MPG REP78 WEIGHT LENGTH FOREIGN 1 AMC 4099 22 3 2930 186 0 2 AMC 4749 17 3 3350 173 0 3 AMC 3799 22 3 2640 168 0 4 Audi 9690 17 5 2830 189 1 5 Audi 6295 23 3 2070 174 1 6 BMW 9735 25 4 2650 177 1 7 Buick 4816 20 3 3250 196 0 8 Buick 7827 15 4 4080 222 0 9 Buick 5788 18 3 3670 218 0 10 Buick 4453 26 3 2230 170 0
2. Descriptive statistics in SAS
We can get descriptive statistics for all of the variables using proc means as shown below.
PROC MEANS DATA=auto; RUN;
Here is the output produced by the proc means statements above.
Variable N Mean Std Dev Minimum Maximum -------------------------------------------------------------------- PRICE 26 6651.73 3371.12 3299.00 15906.00 MPG 26 20.9230769 4.7575042 14.0000000 35.0000000 REP78 26 3.2692308 0.7775702 2.0000000 5.0000000 WEIGHT 26 3099.23 695.0794089 2020.00 4330.00 LENGTH 26 190.0769231 18.1701361 163.0000000 222.0000000 FOREIGN 26 0.2692308 0.4523443 0 1.0000000 --------------------------------------------------------------------
We can get descriptive statistics separately for foreign and domestic cars (i.e., broken down by foreign) as shown below.
PROC MEANS DATA=auto; CLASS foreign; RUN;
The output from the above statements is shown below.
FOREIGN N Obs Variable N Mean Std Dev Minimum
---------------------------------------------------------------------------
0 19 PRICE 19 6484.16 3768.46 3299.00
MPG 19 19.7894737 4.0356598 14.0000000
REP78 19 2.9473684 0.5242650 2.0000000
WEIGHT 19 3347.89 627.1769106 2110.00
LENGTH 19 195.4210526 17.9639014 163.0000000
1 7 PRICE 7 7106.57 2101.83 4589.00
MPG 7 24.0000000 5.5075705 17.0000000
REP78 7 4.1428571 0.6900656 3.0000000
WEIGHT 7 2424.29 325.1593016 2020.00
LENGTH 7 175.5714286 8.4628038 165.0000000
---------------------------------------------------------------------------
FOREIGN N Obs Variable Maximum
-------------------------------------------
0 19 PRICE 15906.00
MPG 29.0000000
REP78 4.0000000
WEIGHT 4330.00
LENGTH 222.0000000
1 7 PRICE 9735.00
MPG 35.0000000
REP78 5.0000000
WEIGHT 2830.00
LENGTH 189.0000000
-------------------------------------------
We can get detailed descriptive statistics for price using proc univariate as shown below.
PROC UNIVARIATE DATA=auto; VAR PRICE; RUN;
The results are shown below.
Univariate Procedure
Variable=PRICE
Moments
N 26 Sum Wgts 26
Mean 6651.731 Sum 172945
Std Dev 3371.12 Variance 11364449
Skewness 1.470727 Kurtosis 1.534672
USS 1.4345E9 CSS 2.8411E8
CV 50.68034 Std Mean 661.131
T:Mean=0 10.06114 Pr>|T| 0.0001
Num ^= 0 26 Num > 0 26
M(Sign) 13 Pr>=|M| 0.0001
Sgn Rank 175.5 Pr>=|S| 0.0001
Quantiles(Def=5)
100% Max 15906 99% 15906
75% Q3 8129 95% 14500
50% Med 5146.5 90% 11385
25% Q1 4453 10% 3799
0% Min 3299 5% 3667
1% 3299
Range 12607
Q3-Q1 3676
Mode 3299
Extremes
Lowest Obs Highest Obs
3299( 17) 9735( 6)
3667( 21) 10372( 12)
3799( 3) 11385( 14)
3955( 22) 14500( 15)
4082( 13) 15906( 16)
We can get a frequency distribution of rep78 (the repair rating of the car) using proc freq as shown below.
PROC FREQ DATA=auto; TABLES rep78 ; RUN;
The results are shown below.
Cumulative Cumulative
REP78 Frequency Percent Frequency Percent
----------------------------------------------------
2 3 11.5 3 11.5
3 15 57.7 18 69.2
4 6 23.1 24 92.3
5 2 7.7 26 100.0
We can make a two way table showing the frequencies for rep78 for foreign and domestic cars as shown below.
PROC FREQ DATA=auto ; TABLES rep78 * foreign ; RUN;
The output is shown below.
TABLE OF REP78 BY FOREIGN
REP78 FOREIGN
Frequency|
Percent |
Row Pct |
Col Pct | 0| 1| Total
---------+--------+--------+
2 | 3 | 0 | 3
| 11.54 | 0.00 | 11.54
| 100.00 | 0.00 |
| 15.79 | 0.00 |
---------+--------+--------+
3 | 14 | 1 | 15
| 53.85 | 3.85 | 57.69
| 93.33 | 6.67 |
| 73.68 | 14.29 |
---------+--------+--------+
4 | 2 | 4 | 6
| 7.69 | 15.38 | 23.08
| 33.33 | 66.67 |
| 10.53 | 57.14 |
---------+--------+--------+
5 | 0 | 2 | 2
| 0.00 | 7.69 | 7.69
| 0.00 | 100.00 |
| 0.00 | 28.57 |
---------+--------+--------+
Total 19 7 26
73.08 26.92 100.00
3. Making graphs in SAS
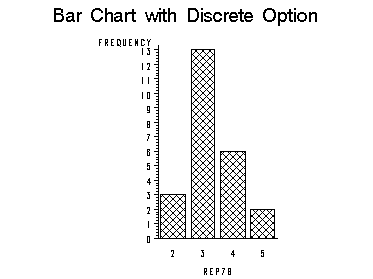
We can make a bar chart showing the frequencies of rep78 as shown below.
TITLE 'Bar Chart with Discrete Option';
PROC GCHART DATA=auto;
VBAR rep78/ DISCRETE;
RUN;
This program produces the following chart.
4. Correlation, regression and analysis of variance
We can use proc corr to get correlations of price mpg weight and length as shown below.
PROC CORR DATA=auto ; VAR price mpg weight length ; RUN;
The output is shown below.
Simple Statistics
Variable N Mean Std Dev Sum Minimum Maximum
PRICE 26 6652 3371 172945 3299 15906
MPG 26 20.92308 4.75750 544.00000 14.00000 35.00000
WEIGHT 26 3099 695.07941 80580 2020 4330
LENGTH 26 190.07692 18.17014 4942 163.00000 222.00000
Pearson Correlation Coefficients / Prob > |R| under Ho: Rho=0 / N = 26
PRICE MPG WEIGHT LENGTH
PRICE 1.00000 -0.43846 0.55607 0.43604
0.0 0.0251 0.0032 0.0260
MPG -0.43846 1.00000 -0.80816 -0.76805
0.0251 0.0 0.0001 0.0001
WEIGHT 0.55607 -0.80816 1.00000 0.90654
0.0032 0.0001 0.0 0.0001
LENGTH 0.43604 -0.76805 0.90654 1.00000
0.0260 0.0001 0.0001 0.0
We can use proc reg to predict mpg from weight length and foreign, as shown below.
PROC REG DATA=auto; MODEL mpg = weight length foreign ; RUN;
The output is shown below.
Model: MODEL1
Dependent Variable: MPG
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Prob>F
Model 3 378.69701 126.23234 14.839 0.0001
Error 22 187.14915 8.50678
C Total 25 565.84615
Root MSE 2.91664 R-square 0.6693
Dep Mean 20.92308 Adj R-sq 0.6242
C.V. 13.93982
Parameter Estimates
Parameter Standard T for H0:
Variable DF Estimate Error Parameter=0 Prob > |T|
INTERCEP 1 44.968582 9.32267757 4.824 0.0001
WEIGHT 1 -0.005008 0.00218752 -2.289 0.0320
LENGTH 1 -0.043056 0.07692650 -0.560 0.5813
FOREIGN 1 -1.269211 1.63213395 -0.778 0.4451
We can use proc glm to do an ANOVA to test if the mean mpg is the same for foreign and domestic cars, as shown below.
PROC GLM DATA=auto; CLASS foreign ; MODEL mpg = foreign ; RUN;
The output is shown below.
General Linear Models Procedure
Class Level Information
Class Levels Values
FOREIGN 2 0 1
Number of observations in data set = 26
General Linear Models Procedure
Dependent Variable: MPG
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 90.68825911 90.68825911 4.58 0.0427
Error 24 475.15789474 19.79824561
Corrected Total 25 565.84615385
R-Square C.V. Root MSE MPG Mean
0.160270 21.26610 4.4495220 20.923077
Source DF Type I SS Mean Square F Value Pr > F
FOREIGN 1 90.68825911 90.68825911 4.58 0.0427
Source DF Type III SS Mean Square F Value Pr > F
FOREIGN 1 90.68825911 90.68825911 4.58 0.0427
