This page shows an example of probit regression analysis with footnotes explaining the output in SAS. The data in this example were gathered on undergraduates applying to graduate school and includes undergraduate GPAs, the reputation of the school of the undergraduate (a topnotch indicator), the students’ GRE score, and whether or not the student was admitted to graduate school. Using this dataset ( https://stats.idre.ucla.edu/wp-content/uploads/2016/02/probit.sas7bdat ), we can predict admission to graduate school using undergraduate GPA, GRE scores, and the reputation of the school of the undergraduate. Our outcome variable is binary, and we will use a probit model. Thus, our model will calculate a predicted probability of admission based on our predictors. The probit model does so using the cumulative distribution function of the standard normal.
First, let us examine the dataset and our response variable. Our binary outcome variable must be coded with zeros and ones, so we will include a frequency of our outcome variable admit to check this.
data probit; set "C:\Data\probit.sas7bdat"; run; proc means data = probit; var gre gpa; run;
The MEANS Procedure Variable N Mean Std Dev Minimum Maximum GRE 400 587.7000000 115.5165364 220.0000000 800.0000000 GPA 400 3.3899000 0.3805668 2.2600000 4.0000000
proc freq data = probit;
table topnotch admit;
run;
The FREQ Procedure
Cumulative Cumulative
TOPNOTCH Frequency Percent Frequency Percent
0 335 83.75 335 83.75
1 65 16.25 400 100.00
Cumulative Cumulative
ADMIT Frequency Percent Frequency Percent
0 273 68.25 273 68.25
1 127 31.75 400 100.00
We have now examined the data and the range of our predictors is acceptable and our outcome variable is properly coded with zeroes and ones. To run a probit model in SAS, we will use proc logistic and specify probit as our link function. By default, SAS predicts the lowest value of the outcome variable. In this case, SAS would thus be predicting admit = 0, or non-admission. Because we are interested in predicting admission (admit = 1), we have indicated that our model is to predict the “event” of admit = 1.
proc logistic data = probit; model admit (event = '1') = gre topnotch gpa / link = probit; run;
NOTE: It is also possible to run a probit regression in SAS using proc probit, though it is more difficult to specify the predicted outcome as we did with (event = ‘1’) using proc logistic. We can order the data so that the predicted outcomes occur first in our dataset, then indicate order = data in our proc probit function.
proc sort data = probit; by descending admit; run;
proc probit data = probit order = data; class admit; model admit = gre topnotch gpa; run;
The output below is from the proc logistic command.
Model Information Data Set WORK.PROBIT Response Variable ADMIT Number of Response Levels 2 Model binary probit Optimization Technique Fisher's scoring Number of Observations Read 400 Number of Observations Used 400
Response Profile
Ordered Total
Value ADMIT Frequency
1 0 273
2 1 127
Probability modeled is ADMIT=1.
Model Convergence Status
Convergence criterion (GCONV=1E-8) satisfied.
Model Fit Statistics
Intercept
Intercept and
Criterion Only Covariates
AIC 501.977 485.887
SC 505.968 501.853
-2 Log L 499.977 477.887
Testing Global Null Hypothesis: BETA=0
Test Chi-Square DF Pr > ChiSq
Likelihood Ratio 22.0897 3 <.0001
Score 21.5235 3 <.0001
Wald 21.5263 3 <.0001
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameter DF Estimate Error Chi-Square Pr > ChiSq
Intercept 1 -2.7978 0.6476 18.6630 <.0001
GRE 1 0.00152 0.000640 5.6661 0.0173
TOPNOTCH 1 0.2730 0.1803 2.2923 0.1300
GPA 1 0.4010 0.1948 4.2370 0.0396
Association of Predicted Probabilities and Observed Responses
Percent Concordant 63.9 Somers' D 0.283
Percent Discordant 35.6 Gamma 0.284
Percent Tied 0.5 Tau-a 0.123
Pairs 34671 c 0.641
Model Information
Model Information Data Seta WORK.PROBIT Response Variableb ADMIT Number of Response Levelsc 2 Modeld binary probit Optimization Techniquee Fisher's scoring
a. Data Set – This is the SAS dataset analyzed with probit regression.
b. Response Variable – This is the outcome (a.k.a. dependent) variable in the probit regression.
c. Number of Response Levels – This is the number of levels of the dependent variable. Our dependent variable has two levels: 0 and 1.
d. Model – This is the model that SAS is fitting. Here, binary refers to the outcome variable (the two levels of admit) and probit refers to the distribution used in fitting the model.
e. Optimization Technique – This refers to the iterative method of estimating the regression parameters. In SAS, the default is method is Fisher’s scoring method, whereas in Stata, it is the Newton-Raphson algorithm. Both techniques yield the same estimate for the regression coefficient; however, the standard errors differ between the two methods. For further discussion, see Regression Models for Categorical and Limited Dependent Variables by J. Scott Long (page 56).
Response Profile
Response Profile Ordered Total Valuef ADMITg Frequencyh 1 0 273 2 1 127 Probability modeled is ADMIT=1.i
f. Ordered Value – This refers to how SAS orders (e.g., models) the levels of the dependent variable, admit.
g. ADMIT – This lists the values in the outcome variable, admit. We can see how these values are ordered by SAS by looking at the corresponding ordered value (superscript f).
h. Total Frequency – This is the observed frequency distribution of subjects in the dependent variable. Of our 400 subjects, 273 were not admitted (admit = 0) and 127 were admitted (admit = 1).
i. Probability modeled is ADMIT = 1 – This indicates the value of our outcome variable that is being modeled. From this, we know to interpret the predicted values from the probit model as the predicted probability of admission (admit = 1).
Model Fit
Model Convergence Statusj Convergence criterion (GCONV=1E-8) satisfied. Model Fit Statistics Intercept Intercept and Criterionk Onlyl Covariatesm AICn 501.977 485.887 SCo 505.968 501.853 -2 Log Lp 499.977 477.887
Testing Global Null Hypothesis: BETA=0 Testq Chi-Squarer DFs Pr > ChiSqt Likelihood Ratiou 22.0897 3 <.0001 Scorev 21.5235 3 <.0001 Waldw 21.5263 3 <.0001
j. Model Convergence Status – This describes whether or not the maximum-likelihood algorithm has converged and what kind of convergence criterion is used for convergence. The default convergence criterion is the relative gradient convergence criterion (GCONV), and the default precision is 10-8.
k. Criterion – These are various measurements used to assess the model fit. See superscripts n, o and p. The first two, Akaike Information Criterion (AIC) and Schwarz Criterion (SC) are variants of negative two times the Log-Likelihood (-2 Log L). AIC and SC penalize the Log-Likelihood by the number of predictors in the model.
l. Intercept Only – This column refers to the respective Criterion statistics with no predictors.
m. Intercept and Covariates – This column corresponds to the respective Criterion statistics for the fitted model. A fitted model includes all predictors and the intercept. We can compare the values in this column with the criteria corresponding Intercept Only value to assess model fit/significance.
n. AIC – This is the Akaike Information Criterion. It is calculated as AIC = -2 Log L + 2((k-1) + s), where k is the number of levels of the outcome variable and s is the number of predictors in the model. AIC is used for the comparison of models from different samples or nonnested models. Ultimately, the model with the smallest AIC is considered the best.
o. SC – This is the Schwarz Criterion. It is defined as – 2 Log L + ((k-1) + s)*log(Σ fi), where fi‘s are the frequency values of the ith observation, and k and s were defined previously. Like AIC, SC penalizes for the number of predictors in the model and the smallest SC is most desirable.
p. -2 Log L – This is negative two times the log likelihood. The -2 Log L is used in hypothesis tests for nested models.
q. Test – These are three asymptotically equivalent Chi-Square tests. They test against the null hypothesis that at least one of the predictors’ regression coefficient is not equal to zero in the model. The differences between the three tests can be attributed to evaluating the log-likelihood function at different points. For further discussion, see Categorical Data Analysis, Second Edition, by Alan Agresti (pages 11-13).
r. Chi-Square – This is the Chi-Square test statistic corresponding to the specific test that all of the predictors are simultaneously equal to zero.
s. DF – This is the number of degrees of freedom. It determines the distribution of the Chi-Square test statistics and is defined by the number of predictors in the model. Our model includes three predictors, so DF = 3.
t. Pr > ChiSq – This is the probability the Chi-Square test statistic (or a more extreme test statistic) would be observed under the null hypothesis that a particular predictor’s regression coefficient is zero, given that the rest of the predictors are in the model. For a given alpha level, Pr > ChiSq determines whether or not the null hypothesis can be rejected. If Pr > ChiSq is less than alpha, then the null hypothesis can be rejected and the parameter estimate is considered statistically significant at that alpha level.
u. Likelihood Ratio – This is the Likelihood Ratio (LR) Chi-Square test that at least one of the predictors’ regression coefficient is not equal to zero in the model. The LR Chi-Square statistic can be calculated by -2 Log L(null model) – 2 Log L(fitted model) = 499.977 – 477.887 = 22.0897, where L(null model) refers to the Intercept Only model and L(fitted model) refers to the Intercept and Covariates model.
v. Score – This is the Score Chi-Square Test that at least one of the predictors’ regression coefficient is not equal to zero in the model.
w. Wald – This is the Wald Chi-Square Test that at least one of the predictors’ regression coefficient is not equal to zero in the model.
Parameter Estimates
Analysis of Maximum Likelihood Estimates
Standard Wald
Parameterx DFy Estimatez Erroraa Chi-Squarebb Pr > ChiSqcc
Intercept 1 -2.7978 0.6476 18.6630 <.0001
GRE 1 0.00152 0.000640 5.6661 0.0173
TOPNOTCH 1 0.2730 0.1803 2.2923 0.1300
GPA 1 0.4010 0.1948 4.2370 0.0396
Association of Predicted Probabilities and Observed Responses
Percent Concordantdd 63.9 Somers' Dhh 0.283
Percent Discordantee 35.6 Gammaii 0.284
Percent Tiedff 0.5 Tau-ajj 0.123
Pairsgg 34671 ckk 0.641
x. Parameter – These refer to the independent variables in the model as well as intercepts (a.k.a. constants) for the adjacent levels of the dependent variable.
y. DF – This column gives the degrees of freedom corresponding to the Parameter. For each Parameter estimated in the model, one DF is required, and the DF defines the Chi-Square distribution to test whether the individual regression coefficient is zero given the other variables are in the model.
z. Estimate – These are the regression coefficients. The predicted probability of admission can be calculated using these coefficients. For a given record, the predicted probability of admission is
![]()
where F is the cumulative distribution function of the standard normal. However, interpretation of the coefficients in probit regression is not as straightforward as the interpretations of coefficients in linear regression or logit regression. The increase in probability attributed to a one-unit increase in a given predictor is dependent both on the values of the other predictors and the starting value of the given predictors. For example, if we hold gre and topnotch constant at zero, the one unit increase in gpa from 2 to 3 has a different effect than the one unit increase from 3 to 4 (note that the probabilities do not change by a common difference or common factor):
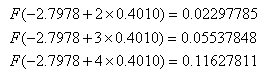
and the effects of these one unit increases are different if we hold gre and topnotch constant at their respective means instead of zero:
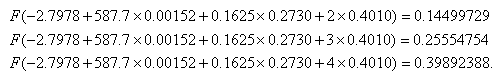
However, there are limited ways in which we can interpret the individual regression coefficients. A positive coefficient mean that an increase in the predictor leads to an increase in the predicted probability. A negative coefficient means that an increase in the predictor leads to a decrease in the predicted probability.
Intercept – The constant term is -2.797884. This means that if all of the predictors (gre, topnotch and gpa) are evaluated at zero, the predicted probability of admission is F(-2.797884) = 0.002571929. So, as expected, the predicted probability of a student with a GRE score of zero and a GPA of zero from a non-topnotch school has an extremely low predicted probability of admission.
gre – The coefficient of gre is 0.0015244. This means that an increase in GRE score increases the predicted probability of admission.
topnotch – The coefficient of topnotch is 0.2730334. This means attending a top notch institution as an undergraduate increases the predicted probability of admission.
gpa – The coefficient of gpa is 0.4009853. This means that an increase in GPA increases the predicted probability of admission.
aa. Standard Error – These are the standard errors of the individual regression coefficients. They are used in the calculation of the Wald Chi-Square test statistic, superscript bb.
bb. Wald Chi-Square – This is the Wald test statistic for the hypothesis test that an individual predictor’s regression coefficient is zero given the rest of the predictors are in the model. The Wald Chi-Square test statistic is the squared ratio of the Estimate to the Standard Error of the respective predictor. The probability that a particular Wald Chi-Square test statistic is as extreme as, or more so, than what has been observed under the null hypothesis is given by Pr > ChiSq.
cc. Pr > ChiSq – This is the p-value corresponding to the Wald Chi-Square test statistic that all of the predictors are simultaneously equal to zero. We are testing the probability (Pr > ChiSq) of observing a Chi-Square statistic as extreme as, or more so, than the observed one under the null hypothesis; the null hypothesis is that all of the regression coefficients in the model are equal to zero. Typically, Pr > ChiSq is compared to a specified alpha level, our willingness to accept a type I error, which is typically set at 0.05 or 0.01. The small p-value from the all three tests would lead us to conclude that at least one of the regression coefficients in the model is not equal to zero
The Wald Chi-Square test statistic for the Intercept is 18.6630 with an associated p-value <.0001. If we set our alpha level to 0.05, we would reject the null hypothesis and conclude that the model intercept has been found to be statistically different from zero given gre, topnotch and gpa are in the model.
The Wald Chi-Square test statistic for the predictor gre is 5.6661 with an associated p-value of 0.0173. If we set our alpha level to 0.05, we would reject the null hypothesis and conclude that the regression coefficient for gre has been found to be statistically different from zero in estimating gre given topnotch and gpa are in the model.
The Wald Chi-Square test statistic for the predictor topnotch is 2.2923 with an associated p-value of 0.1300. If we set our alpha level to 0.05, we would fail to reject the null hypothesis and conclude that the regression coefficient for topnotch has not been found to be statistically different from zero in estimating topnotch given gre and gpa are in the model.
The Wald Chi-Square test statistic for the predictor gpa is 4.2370 with an associated p-value of 0.0396. If we set our alpha level to 0.05, we would reject the null hypothesis and conclude that the regression coefficient for gpa has been found to be statistically different from zero in estimating gpa given topnotch and gpa are in the model.
dd. Percent Concordant – A pair of observations with different observed responses is said to be concordant if the observation with the lower ordered response value has a lower predicted mean score than the observation with the higher ordered response value.
ee. Percent Discordant – If the observation with the lower ordered response value has a higher predicted mean score than the observation with the higher ordered response value, then the pair is discordant.
ff. Percent Tied – If a pair of observations with different responses is neither concordant nor discordant, it is a tie.
gg. Pairs – This is the total number of distinct pairs with one case having a positive response (admit = 1) and the other having a negative response (admit = 0). The total number of ways the 400 observations can be paired up (excluding be matched up with themselves) is 400(399)/2 = 79,800. Of the 79,800 possible pairings, 34,671 have different values on the response variable and 79,800 – 34,671 = 45,129 have the same value on the response variable.
hh. Somers’ D – Somer’s D is used to determine the strength and direction of relation between pairs of variables. Its values range from -1.0 (all pairs disagree) to 1.0 (all pairs agree). It is defined as (nc-nd)/t where nc is the number of pairs that are concordant, and nd the number of pairs that are discordant, and t is the number of total number of pairs with different responses. In our example, it equals the difference between the percent concordant and the percent discordant divided by 100: (63.9-35.6)/100 = 0.283.
ii. Gamma – The Goodman-Kruskal Gamma method does not penalize for ties on either variable. Its values range from -1.0 (no association) to 1.0 (perfect association). Because it does not penalize for ties, its value will generally be greater than the values for Somer’s D.
jj. Tau-a – Kendall’s Tau-a is a modification of Somer’s D to take into the account the difference between the number of possible paired observations and the number of paired observations with different response. It is defined to be the ratio of the difference between the number of concordant pairs and the number of discordant pairs to the number of possible pairs (2(nc-nd)/(N(N-1)). Usually Tau-a is much smaller than Somer’s D since there would be many paired observations with the same response.
kk. c – Another measure of rank correlation of ordinal variables. It ranges from 0 to (no association) to 1 (perfect association). It is a variant of Somer’s D index.
