Robust regression models are often used to detect outliers and to provide stable estimates in the presence of outliers. Procedure ROBUSTREG in SAS 9 has implemented four common methods of performing robust regression. This page will show some examples on how to perform different types of robust regression analysis using proc robustreg. The examples are mainly taken from Modern Applied Statistics with S (4th edition, page 158 – 161) and the data set by Rousseeuw and Leroy on annual numbers of Belgian telephone calls, phones.sas7bdat, is used and can be downloaded here.
1. What are outliers?
Outliers are data points with extreme values in a random sample. For a regression analysis, there are basically two ways that a data point can be extreme. It can be extreme in the direction of the outcome variable (y-direction). It can also be a multivariate outlier in the predictor space (x-direction), which is also referred as a leverage point. Sometimes, an outlier can be both in the direction of the y-direction and x-direction, which is also called an influence point. Outliers can yield biased estimation of regression parameters.
Let us take a look at some extremely simple-minded examples. Data set demo0 has three data points. We should be able to tell that by design, the regression line is close to each point and this is shown by the scatter plot below. There are no outliers in this data set.
data demo0; input y x; datalines; 2.3 0 3.3 1 4.4 2 ; run; symbol i = r v=star l=2 ci=red cv=black; proc gplot data = demo; plot y*x; run; quit;
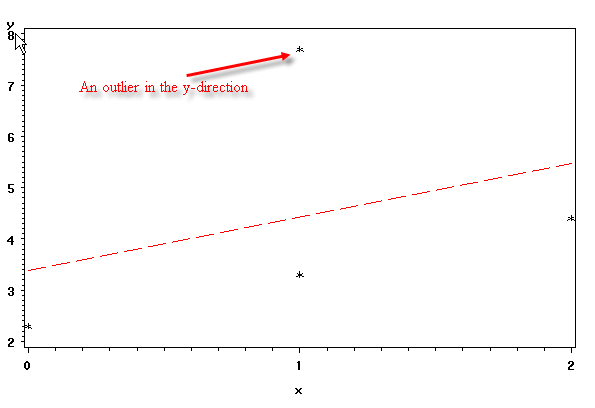
How can a point be a outlier in the direction of y? The data point simply takes extreme value in y. For example, in our next data set demo1, we have added one point (1, 7,7). In terms of x-direction, it is right in the middle, but in terms of y-direction, it is way up. You can see that the residual for this point is particular large than those of other data points. The regression line is then lifted upwards, but the slope of the regression does not change much.
data demo1; input y x; datalines; 2.3 0 3.3 1 4.4 2 7.7 1 ; run; symbol i = r v=star l=2 ci=red cv=black; proc gplot data = demo1; plot y*x; run; quit;
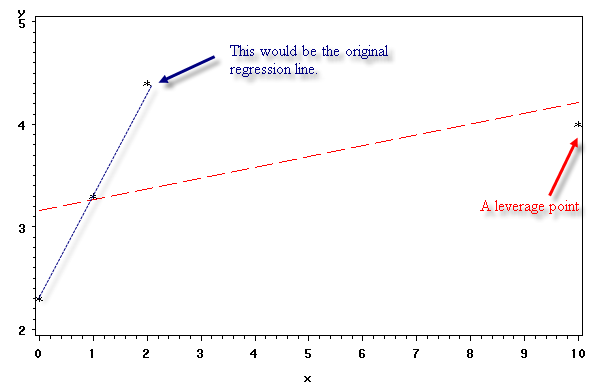
Now let us create a data point that is leverage point, that is outlier in the x-direction. We add one point (10, 4). It is extreme in the x-direction. Notice that the residual of this point is not particularly larger than that of any other points, but the slope has changed greatly. That is why outliers in the x-direction are also called leverage points, since they "leverage" the regression line.
data demo2; input y x; datalines; 2.3 0 3.3 1 4.4 2 4 10 ; run; proc gplot data = demo2; plot y*x; run; quit;
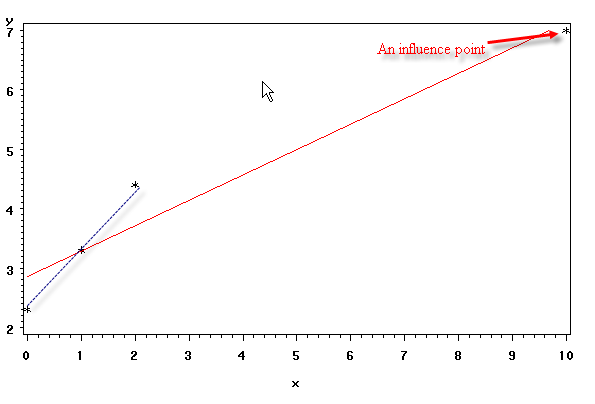
Last but not least, let us create an example with an influence point. To this end, we just need to add a point for which both the y-direction and x-direction are extreme. An influence point affects both the intercept and the slope of a regression model.
data demo2; input y x; datalines; 2.3 0 3.3 1 4.4 2 7 10 ; run; symbol1 i = r v=star cv=black ci=red; proc gplot data = demo2; plot y*x; run; quit;
If these static examples have not satisfied your curiosity, you can play a regression applet developed by Professor West of University of South Carolina.
2. Detection of outliers and Remedies
Now we know what outliers are, the question is how to detect them and what to do after we detect them.
2. M estimation
Introduced by Huber in 1973, M-estimators have been widely used in models where outliers are in the direction of the outcome variable. Each M-estimator corresponds to a specific weight function. Some commonly used weight functions are Huber weight function and bisquare weight function. Notice that OLS regression can be considered as a special case of M-estimator, where the weight function is the identity function. The Robustreg procedure offers ten kinds of weight functions. For details on the definition of weight functions and their shapes, please visit SAS’s page on the
weight functions.
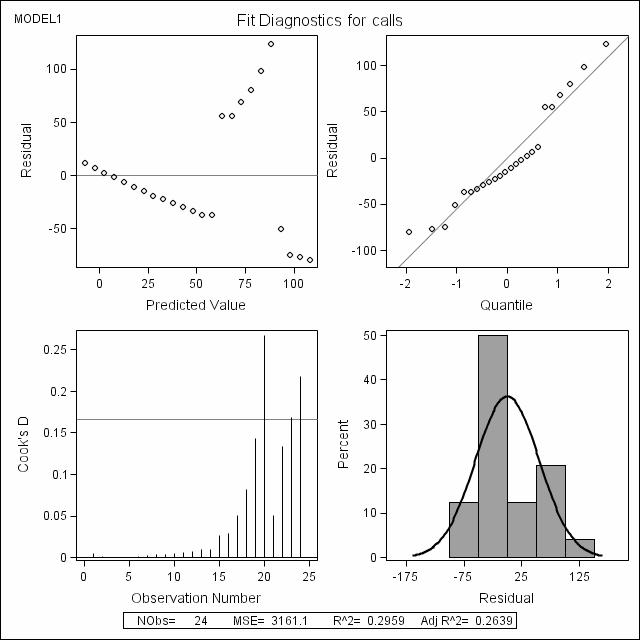
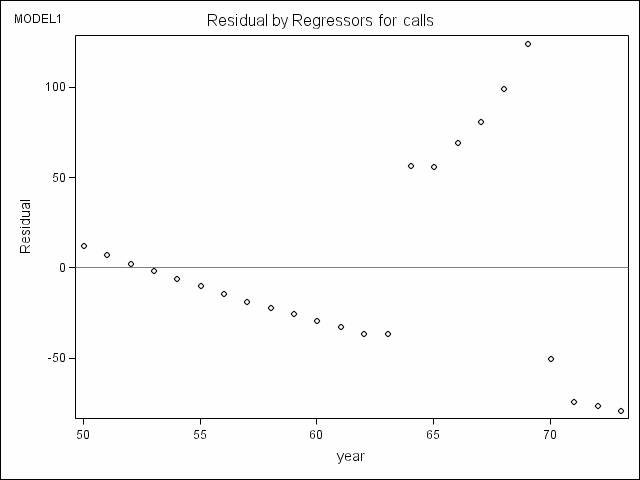
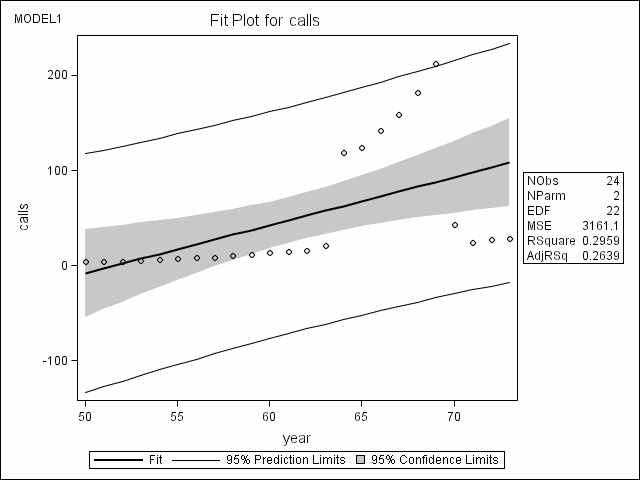
Example 1. OLS regression with identical weight function by proc reg; the first model on page 159. This example is mainly used for comparison with the robust regression models. To this end, we will also make use ODS graphics facility of SAS 9 to create diagnostics plots.
ods html style = journal; ods graphics on; proc reg data = phones; model calls = year; run; quit; ods graphics off; ods html close;
Analysis of Variance
Sum of Mean Source DF Squares Square F Value Pr > F
Model 1 29229 29229 9.25 0.0060 Error 22 69544 3161.06999 Corrected Total 23 98773
Root MSE 56.22339 R-Square 0.2959 Dependent Mean 49.99167 Adj R-Sq 0.2639 Coeff Var 112.46553
Parameter Estimates
Parameter Standard Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 -260.05925 102.60700 -2.53 0.0189 year year 1 5.04148 1.65794 3.04 0.0060
Example 2. M-estimator with Huber’s weight function, the second model on page 159.
proc robustreg data = phones method = m (wf=huber); model calls = year; run;
The ROBUSTREG Procedure
Model Information
Data Set WORK.PHONES Dependent Variable calls calls Number of Independent Variables 1 Number of Observations 24 Method M Estimation
Number of Observations Read 24 Number of Observations Used 24
Summary Statistics
Standard Variable Q1 Median Q3 Mean Deviation MAD
year 55.5000 61.5000 67.5000 61.5000 7.0711 8.8956 calls 7.7000 15.5000 81.0000 49.9917 65.5321 15.1225
Parameter Estimates
Standard 95% Confidence Chi- Parameter DF Estimate Error Limits Square Pr > ChiSq
Intercept 1 -102.530 26.4920 -154.454 -50.6067 14.98 0.0001 year 1 2.0396 0.4281 1.2006 2.8786 22.70 <.0001 Scale 1 9.0093
Diagnostics Summary
Observation Type Proportion Cutoff
Outlier 0.2500 3.0000
Goodness-of-Fit
Statistic Value
R-Square 0.1780 AICR 229.6477 BICR 230.6074 Deviance 18201.95
Example 3: M-estimator with Huber’s weight and Huber’s scale, the third model on page 159.
proc robustreg data = phones method = m (scale=huber wf=huber);
model calls = year;
run;
Parameter Estimates
Standard 95% Confidence Chi-
Parameter DF Estimate Error Limits Square Pr > ChiSq
Intercept 1 -227.818 101.7708 -427.285 -28.3510 5.01 0.0252
year 1 4.4511 1.6444 1.2280 7.6741 7.33 0.0068
Scale 1 57.1905
Diagnostics Summary
Observation
Type Proportion Cutoff
Outlier 0.0000 3.0000
Goodness-of-Fit
Statistic Value
R-Square 0.2268
AICR 23.2133
BICR 26.5904
Deviance 66181.33
3.
Least Trimmed Squares estimation (LTS)
4.
S estimation
5. MM estimation
Online References
-
Colin Chen, Robust Regression and Outlier Detection with the ROBUSTREG Procedure, SUGI 27
-
J. W. Osborne, The power of outliers (and why researchers should ALWAYS check for them), Practical Assessment, Research & Evaluation (2004)