Multiple Imputation in SAS Part 1

Note: A PowerPoint presentation of this webpage can be downloaded here.

Introduction

Missing data is a common issue, and more often than not, we deal with the matter of missing data in an ad hoc fashion. The purpose of this seminar is to discuss commonly used techniques for handling missing data and common issues that could arise when these techniques are used. In particular, we will focus on the one of the most popular methods, multiple imputation. We are not advocating in favor of any one technique to handle missing data and depending on the type of data and model you will be using, other techniques such as direct maximum likelihood may better serve your needs. We have chosen to explore multiple imputation through an examination of the data, a careful consideration of the assumptions needed to implement this method and a clear understanding of the analytic model to be estimated. We hope this seminar will help you to better understand the scope of the issues you might face when dealing with missing data using this method.

The data set hsb_mar.sas7bdat  which is based on hsb2.sas7bdat used for this seminar can be downloaded from the link. The SAS code for this seminar is developed using SAS 9.4 and SAS/STAT 13.1. Some of the variables have value labels (formats) associated with them. Here is the setup for reading the value labels correctly.

proc format;
  value female 0 = "male"
               1= "female";
  value prog 1 = "general"
             2 = "academic"
             3 = "vocation" ;
  value race 1 = "hispanic"
             2 = "asian"
             3 = "african-amer"
             4 = "white";
  value schtyp 1 = "public"
               2 = "private";
  value ses  1 =  "low"
             2 = "middle"
             3 = "high";
run;
options fmtsearch=(work);

Goals of statistical analysis with missing data:

• Minimize bias
• Maximize use of available information
• Obtain appropriate estimates of uncertainty

Exploring missing data mechanisms

The missing data mechanism describes the process that is believed to have generated the missing values. Missing data mechanisms generally fall into one of three main categories. There are precise technical definitions for these terms in the literature; the following explanation necessarily contains simplifications.

• Missing completely at random (MCAR)

A variable is missing completely at random if neither the variables in the dataset nor the unobserved value of the variable itself predict whether a value will be missing. Missing completely at random is a fairly strong assumption and may be relatively rare. One relatively common situation in which data are missing completely at random occurs when a subset of cases is randomly selected to undergo additional measurement, this is sometimes referred to as “planned missing.” For example, in some health surveys, some subjects are randomly selected to undergo more extensive physical examination; therefore only a subset of participants will have complete information for these variables. Missing completely at random also allow for missing on one variable to be related to missing on another, e.g. var1 is missing whenever var2 is missing. For example, a husband and wife are both missing information on height.

• Missing at random (MAR)

A variable is said to be missing at random if other variables (but not the variable itself) in the dataset can be used to predict missingness on a given variable. For example, in surveys, men may be more likely to decline to answer some questions than women (i.e., gender predicts missingness on another variable). MAR is a less restrictive assumption than MCAR.  Under this assumption the probability of missingness does not depend on the true values after controlling for the observed variables. MAR is also related to ignorability. The missing data mechanism is said be ignorable if it is missing at random and the probability of a missingness does not depend on the missing information itself. The assumption of ignorability is needed for optimal estimation of missing information and is a required assumption for both of the missing data techniques we will discuss.

• Missing not at random (MNAR)

Finally, data are said to be missing not at random if the value of the unobserved variable itself predicts missingness. A classic example of this is income.  Individuals with very high incomes are more likely to decline to answer questions about their income than individuals with more moderate incomes.

An understanding of the missing data mechanism(s) present in your data is important because different types of missing data require different treatments. When data are missing completely at random, analyzing only the complete cases will not result in biased parameter estimates (e.g., regression coefficients). However, the sample size for an analysis can be substantially reduced, leading to larger standard errors. In contrast, analyzing only complete cases for data that are either missing at random, or missing not at random can lead to biased parameter estimates. Multiple imputation and other modern methods such as direct maximum likelihood generally assumes that the data are at least MAR, meaning that this procedure can also be used on data that are missing completely at random. Statistical models have also been developed for modeling the MNAR processes; however, these model are beyond the scope of this seminar.

For more information on missing data mechanisms please see:

• Allison, 2002
• Enders, 2010
• Little & Rubin, 2002
• Rubin, 1976
• Schafer & Graham, 2002

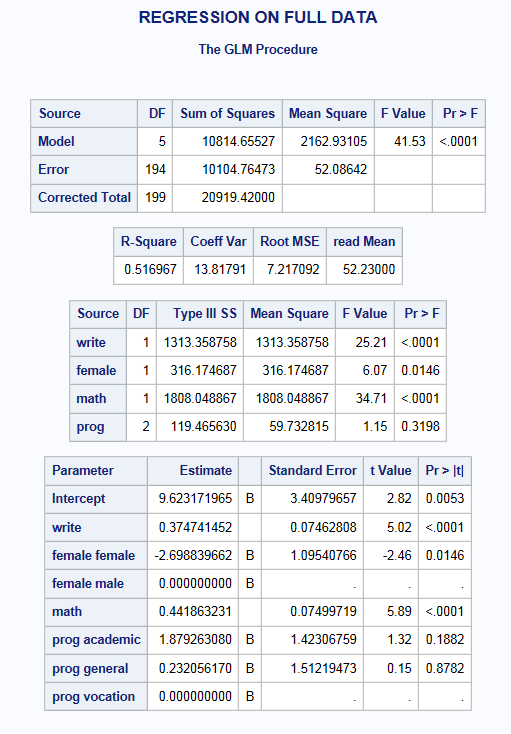
Full data:

Below is a regression model predicting read using the complete data set (hsb2) used to create hsb_mar. We will use these results for comparison.

 

Common techniques for dealing with missing data

In this section, we are going to discuss some common techniques for dealing with missing data and briefly discuss their limitations.

• Complete case analysis (listwise deletion)
• Available case analysis (pairwise deletion)
• Mean Imputation
• Single Imputation
• Stochastic Imputation

1. Complete Case Analysis:

This methods involves deleting cases in a particular dataset that are missing data on any variable of interest. It is a common technique because it is easy to implement and works with any type of analysis.

Below we look at some of the descriptive statistics of the data set hsb_mar, which contains test scores, as well as demographic and school information for 200 high school students.

proc means data = ats.hsb_mar nmiss N min max mean std;
  var _numeric_ ;
run; 

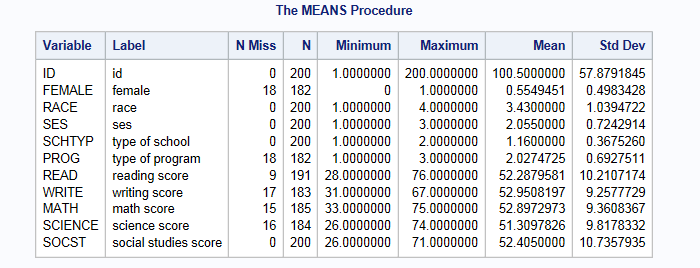
Note that although the dataset contains 200 cases, six of the variables have fewer than 200 observations. The missing information varies between 4.5% (read) and 9% (female and prog) of cases depending on the variable. This doesn’t seem like a lot of missing data, so we might be inclined to try to analyze the observed data as they are, a strategy sometimes referred to as complete case analysis.

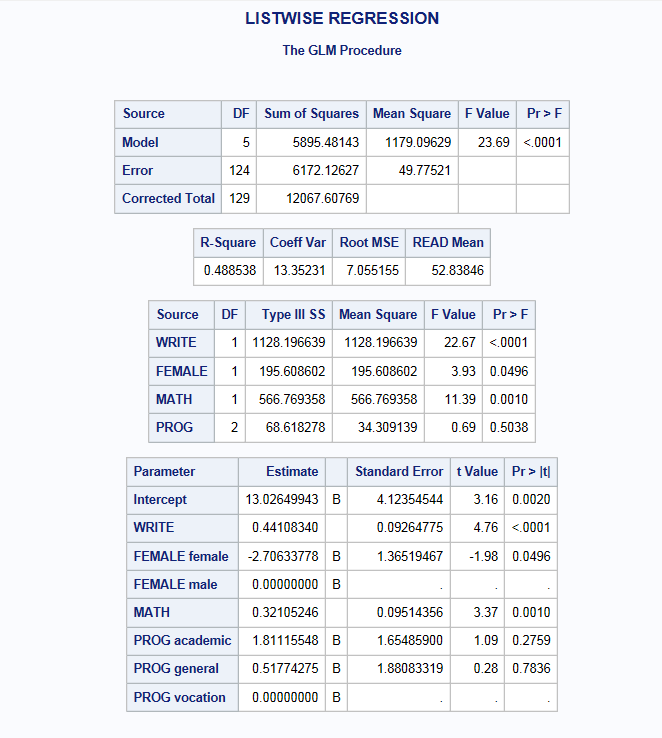
Below is a regression model where the dependent variable read is regressed on write, math, female and prog. Notice that the default behavior of proc glm is complete case analysis (also referred to as listwise deletion).

TITLE " LISTWISE REGRESSION";
proc glm data = ats.hsb_mar;
class female (ref=last) prog;
model read = write female math prog /solution ss3;
run;
quit;

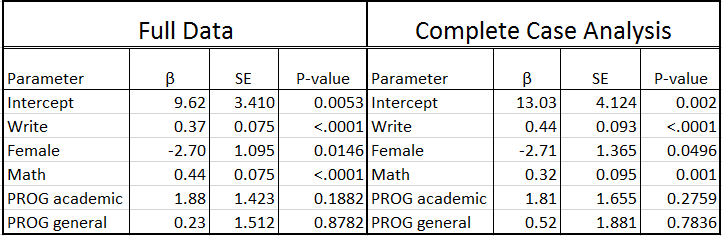
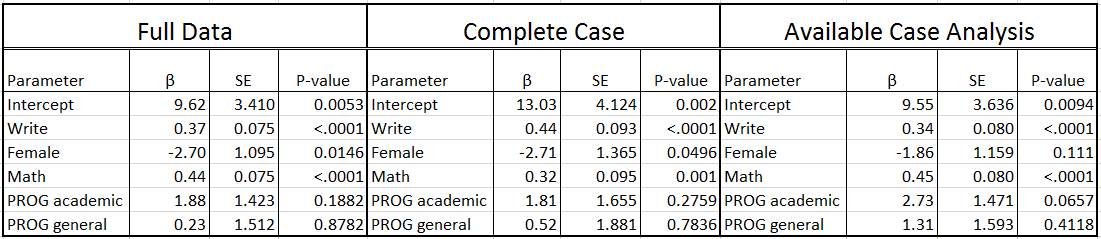
Looking at the output, we see that only 130 cases were used in the analysis; in other words, more than one third of the cases in our dataset (70/200) were excluded from the analysis because of missing data. The reduction in sample size (and statistical power) alone might be considered a problem, but complete case analysis can also lead to biased estimates. Specifically you will see below that the estimates for the intercept, write, math and prog are different from the regression model on the complete data. Also, the standard errors are all larger due to the smaller sample size, resulting in the parameter estimate for female almost becoming non-significant.  Unfortunately, unless the mechanism of missing data is MCAR, this method will introduce bias into the parameter estimates.

2. Available Case Analysis:

This method involves estimating means, variances and covariances based on all available non-missing cases. Meaning that a covariance (or correlation) matrix is computed where each element is based on the full set of cases with non-missing values for each pair of variables. This method became popular because the loss of power due to missing information is not as substantial as with complete case analysis. Below we look at the pairwise correlations between the outcome read and each of the predictors, write, prog, female,and math.  Depending on the pairwise comparison examined, the sample size will change based on the amount of missing present in one or both variables.

Because proc glm does not accept covariance matrices as data input, the following example will be done with proc reg. This will require us to create dummy variables for our categorical predictor prog since there is no class statement in proc reg.

data new;
set ats.hsb_mar;
if prog ^=. then do;
if prog =1 then progcat1=1;
else progcat1=0;
if prog =2 then progcat2=1;
else progcat2=0;
end;
run;

By default proc corr uses pairwise deletion to estimate the correlation table.

TITLE " PAIRWISE CORRELATIONS";
proc corr data = new cov outp=test;
var write read female math progcat1 progcat2 ;
run;

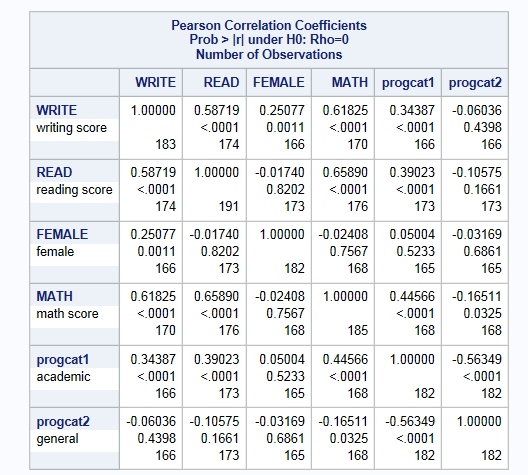
The options on the proc corr statement, cov and outp, will output a variance/covariance matrix based on pairwise deletion that will be used in the subsequent regression model

TITLE" AVAILABLE CASE REGRESSION";
proc reg data = test;
model read = write female math progcat1 progcat2 ;
run;
quit;

 

 

 

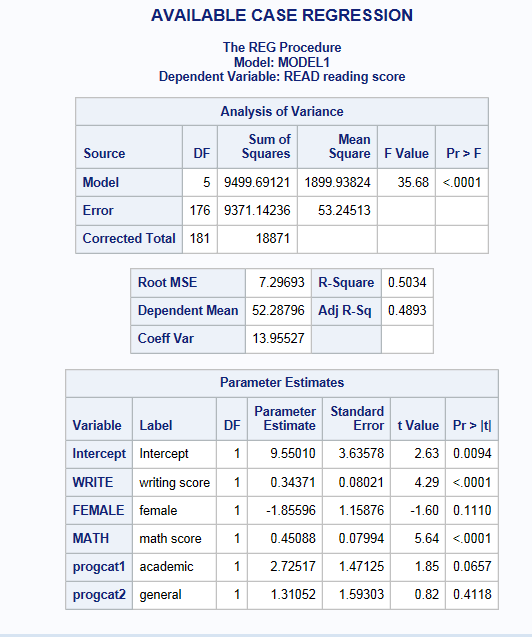
The first thing you should see is the note that SAS prints to your log file stating “N not equal across variables in data set. This may not be appropriate. The smallest value will be used.”.  One of the main drawbacks of this method is no consistent sample size. You will also notice that the parameter estimates presented here are different than the estimates obtained from analysis on the full data and the listwise deletion approach. For instance, the variable female had an estimated effect of -2.7 with the full data but was attenuated to -1.85 for the available case analysis. Unless the mechanism of missing data is MCAR, this method will introduce bias into the parameter estimates. Therefore, this method is not recommended.

 

 

3. Unconditional Mean Imputation

 

This methods involves replacing the missing values for an individual variable with it’s overall estimated mean from the available cases. While this is a simple and easily implemented method for dealing with missing values it has some unfortunate consequences. The most important problem with mean imputation, also called mean substitution, is that it will result in an artificial reduction in variability due to the fact you are imputing values at the center of the variable’s distribution. This also has the unintended consequence of changing the magnitude of correlations between the imputed variable and other variables. We can demonstrate this phenomenon in our data.

 

Below are tables of the means and standard deviations of the four variables in our regression model BEFORE and AFTER a mean imputation as well as their corresponding correlation matrices. We will again utilize the prog dummy variables we created previously.

 

 

 

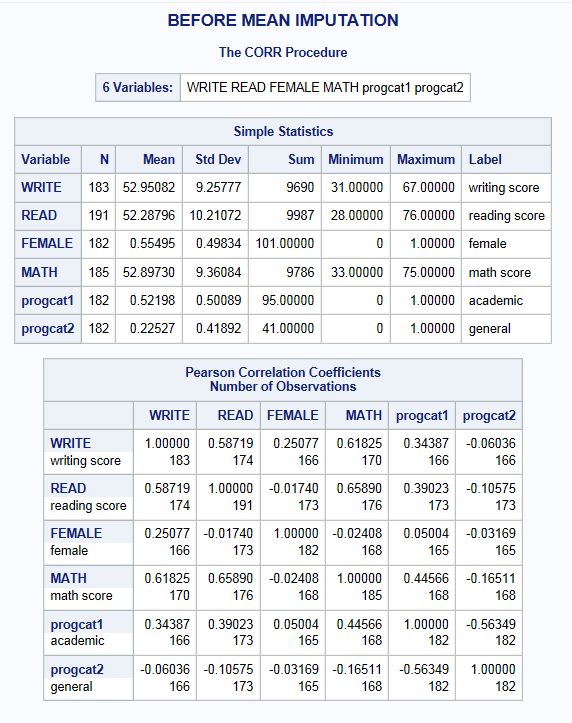
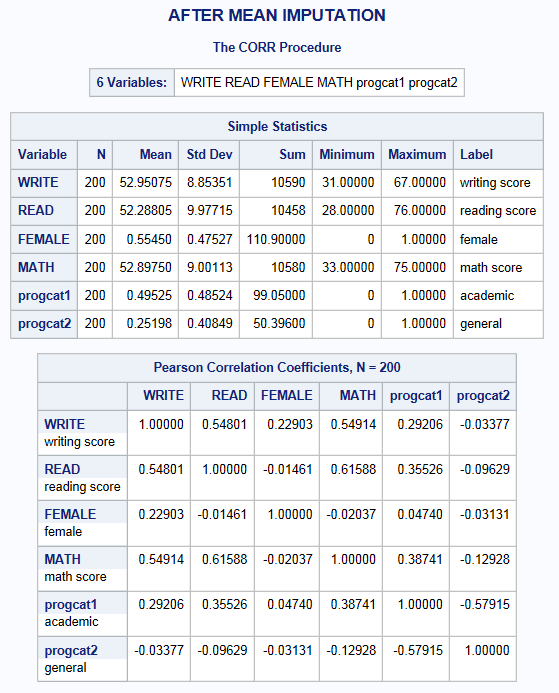
You will notice that there is very little change in the mean (as you would expect); however, the standard deviation is noticeably lower after substituting in mean values for the observations with missing information. This is because you reduce the variability in your variables when you impute everyone at the mean.  Moreover, you can see the table of “Pearson Correlation Coefficients” that the correlation between each of our predictors of interest ( write , math , female , and prog) as well as between predictors and the outcome read have now be attenuated. Therefore, regression models that seek to estimate the associations between these variables will also see their effects weakened.

4. Single or Deterministic Imputation

A slightly more sophisticated type of imputation is a regression/conditional mean imputation, which replaces missing values with predicted scores from a regression equation. The strength of this approach is that it uses complete information to impute values. The drawback here is that all your predicted values will fall directly on the regression line once again decreasing variability, just not as much as with unconditional mean imputation. Moreover, statistical models cannot distinguish between observed and imputed values and therefore do not incorporate into the model the error or uncertainly associated with that imputed value. Additionally, you will see that this method will also inflate the associations between variables because it imputes values that are perfectly correlated with one another. Unfortunately, even under the assumption of MCAR, regression imputation will upwardly bias correlations and R-squared statistics. Further discussion and an example of this can be found in Craig Enders book “Applied Missing Data Analysis” (2010).

5. Stochastic Imputation

In recognition of the problems with regression imputation and the reduced variability associated with this approach, researchers developed a technique to incorporate or “add back” lost variability. A residual term, that is randomly drawn from a normal distribution with mean zero and variance equal to the residual variance from the regression model, is added to the predicted scores from the regression imputation thus restoring some of the lost variability. This method is superior to the previous methods as it will produce unbiased coefficient estimates under MAR. However, the standard errors produced during regression estimation while less biased than the single imputation approach, will still be attenuated.

While you might be inclined to use one of these more traditional methods, consider this statement: “Missing data analyses are difficult because there is no inherently correct methodological procedure. In many (if not most) situations, blindly applying maximum likelihood estimation or multiple imputation will likely lead to a more accurate set of estimates than using one of the [previously mentioned] missing data handling techniques” (p.344, Applied Missing Data Analysis, 2010).

Multiple Imputation

Multiple imputation is essentially an iterative form of stochastic imputation. However, instead of filling in a single value, the distribution of the observed data is used to estimate multiple values that reflect the uncertainty around the true value. These values are then used in the analysis of interest, such as in a OLS model, and the results combined. Each imputed value includes a random component whose magnitude reflects the extent to which other variables in the imputation model cannot predict it’s true values (Johnson and Young, 2011; White et al, 2010). Thus, building into the imputed values a level of uncertainty around the “truthfulness” of the imputed values.

A common misconception of missing data methods is the assumption that imputed values should represent “real” values. The purpose when addressing missing data is to correctly reproduce the variance/covariance matrix we would have observed had our data not had any missing information.

MI has three basic phases:

 

1. Imputation or Fill-in Phase: The missing data are filled in with estimated values and a complete data set is created. This process of fill-in is repeated m times.

 

2. Analysis Phase: Each of the m complete data sets is then analyzed using a statistical method of interest (e.g. linear regression).

 

3. Pooling Phase: The parameter estimates (e.g. coefficients and standard errors) obtained from each analyzed data set are then combined for inference.

 

The imputation method you choose depends on the pattern of missing information as well as the type of variable(s) with missing information.

 

Imputation Model, Analytic Model and Compatibility

 

When developing your imputation model, it is important to assess if your imputation model is “congenial” or consistent with your analytic model. Consistency means that your imputation model includes (at the very least) the same variables that are in your analytic or estimation model. This includes any transformations to variables that will be needed to assess your hypothesis of interest. This can include log transformations, interaction terms, or recodes of a continuous variable into a categorical form, if that is how it will be used in later analysis. The reason for this relates back to the earlier comments about the purpose of multiple imputation. Since we are trying to reproduce the proper variance/covariance matrix for estimation, all relationships between our analytic variables should be represented and estimated simultaneously. Otherwise, you are imputing values assuming they have a correlation of zero with the variables you did not include in your imputation model.  This would result in underestimating the association between parameters of interest in your analysis and a loss of power to detect properties of your data that may be of interest such as non-linearities and statistical interactions. For additional reading on this particular topic see:

 

1. von Hippel, 2009

 

2. von Hippel, 2013

 

3. White et al., 2010

 

Preparing to conduct MI:

 

First step: Examine the number and proportion of missing values among your variables of interest.

 

The proc means procedure in SAS has an option called nmiss that will count the number of missing values for the variables specified.

 

proc means data=ats.hsb_mar nmiss; 
var female write read math prog;
run;

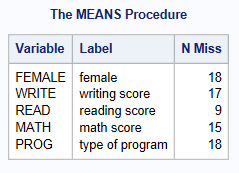
You can also create missing data flags or indicator variables for the missing information to assess the proportion of missingness.

data hsb_flag;
set new;
if female =.  then female_flag =1; else female_flag =0;
if write  = . then write_flag  =1; else write_flag  =0;
if read   = . then read_flag   =1; else read_flag   =0;
if math   = . then math_flag   =1; else math_flag   =0;
if prog   = . then prog_flag   =1; else prog_flag   =0;
run;

proc freq data=hsb_flag;
tables female_flag write_flag read_flag math_flag prog_flag;
run;

 

 

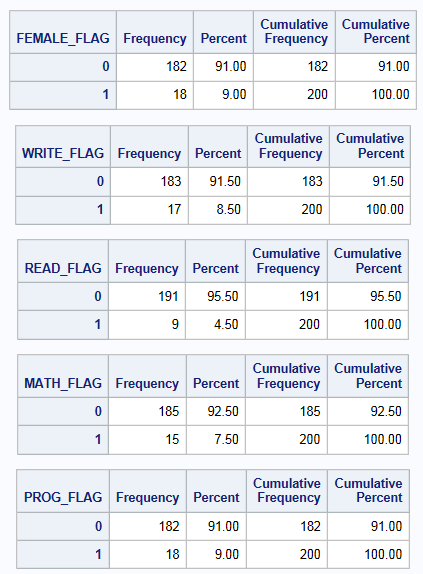
We can see that the variables with the highest proportion of missing information are prog and female with 9.0%. In general, you want to note the variable(s) with a high proportion of missing information as they will have the greatest impact on the convergence of your specified imputation model.

 

Second Step: Examine Missing Data Patterns among your variables of interest.

 

The proc mi procedure has an ods option called misspattern that will output a table of the missing data patterns present in your data file.

 

 

proc mi data=HSB_flag nimpute=0 ;
var socst write read female math prog;
ods select misspattern;
run;

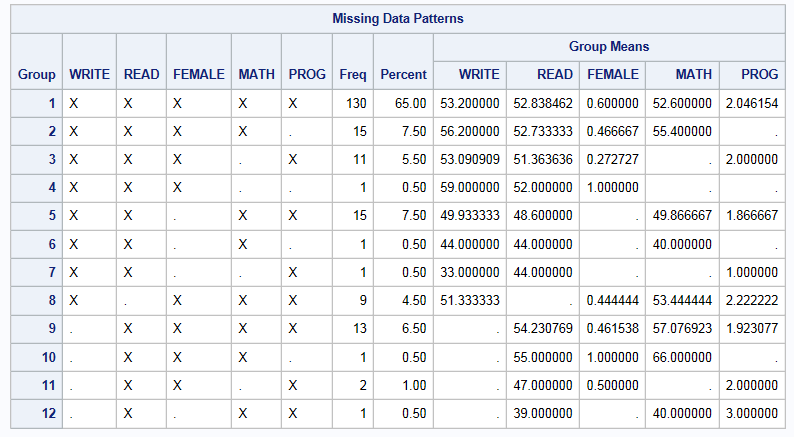
This “Missing Data Patterns” table can be requested without actually performing a full imputation by specifying the option nimpute=0 (specifying zero imputed datasets to be created) on the proc mi statement line. Each “group” represents a set of observations in the data set that share the same pattern of missing information. For example, group 1 represents the 130 observations in the data that have complete information on all 5 variables of interest. This procedure also provides means for each variable for this group. You can see that there are a total of 12 patterns for the specified variables. The estimated means associated with each missing data pattern can also give you an indication of whether the assumption MCAR or MAR is appropriate. If you begin to observe that those with certain missing data patterns appear to have a very different distribution of values, this is an indication that you data may not be MCAR. Moreover, depending on the nature of the data, you may recognize patterns such as monotone missing which can be observed in longitudinal data when an individual drops out at a particular time point and therefore all data after that is subsequently missing. Additionally, you may identify skip patterns that were missed in your original review of the data that should then be dealt with before moving forward with the multiple imputation.

Third Step: If necessary, identify potential auxiliary variables

Auxiliary variables are variables in your data set that are either correlated with a missing variable(s) (the recommendation is r > 0.4) or are believed to be associated with missingness. These are factors that are not of particular interest in your analytic model , but they are added to the imputation model to increase power and/or to help make the assumption of MAR more plausible. These variables have been found to improve the quality of imputed values generate from multiple imputation. Moreover, research has demonstrated their particular importance when imputing a dependent variable and/or when you have variables with a high proportion of missing information (Johnson and Young, 2011; Young and Johnson, 2010; Enders , 2010).

You may a priori know of several variables you believe would make good auxiliary variables based on your knowledge of the data and subject matter. Additionally, a good review of the literature can often help identify them as well. However, if your not sure what variables in the data would be potential candidates (this is often the case when conducting analysis secondary data analysis), you can uses some simple methods to help identify potential candidates. One way to identify these variables is by examining associations between write, read, female, and math with other variables in the dataset.  For example, let’s take a look at the correlation matrix between our 4 variables of interest and two other test score variables science and socst.

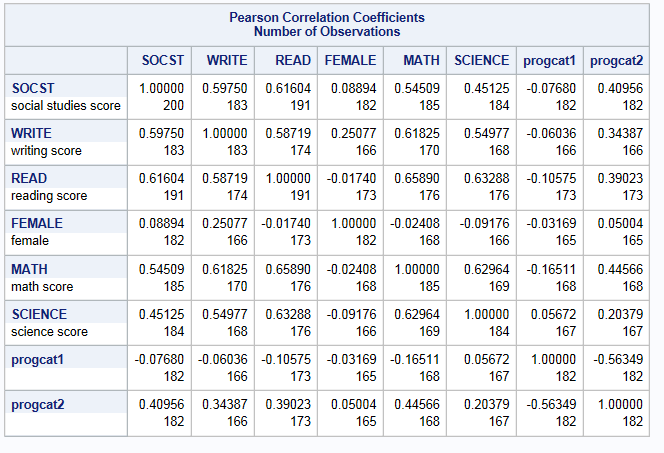
Science and socst both appear to be a good auxiliary because they are well correlated (r >0.4) with all the other test score variables of interest. You will also notice that they are not well correlated with female. A good auxiliary does not have to be correlated with every variable to be used. You will also notice that science also has missing information of it’s own. Additionally, a good auxiliary is not required to have complete information to be valuable. They can have missing and still be effective in reducing bias (Enders, 2010).

One area, this is still under active research, is whether it is beneficial to include a variable as an auxiliary if it does not pass the 0.4 correlation threshold with any of the variables to be imputed. Some researchers believe that including these types of items introduces unnecessary error into the imputation model (Allison, 2012), while others do not believe that there is any harm in this practice (Ender, 2010). Thus. we leave it up to you as the researcher to use your best judgment.

Good auxiliary variables can also be correlates or predictors of missingness. Let’s use the missing data flags we made earlier to help us identify some variables that may be good correlates. We examine if our potential auxiliary variable socst also appears to predict missingness. Below are a set of t-tests to test if the mean socst or science scores differ significantly between those with missing information and those without.

proc ttest data=hsb_flag;
var socst science;
class read_flag;
run;

proc ttest data=hsb_flag;
var socst science;
class write_flag;
run;

proc ttest data=hsb_flag;
var socst science;
class math_flag;
run;

proc ttest data=hsb_flag;
var socst science;
class female_flag;
run;

proc ttest data=hsb_flag;
var socst science;
class prog_flag;
run;

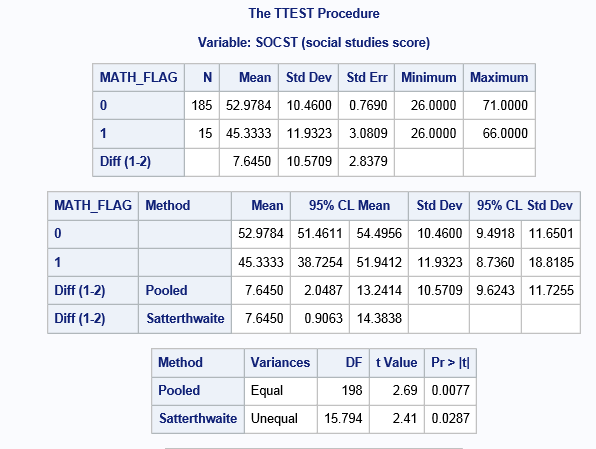
The only significant difference was found when examining missingness on math with socst. Above you can see that the mean socst score is significantly lower among the respondents who are missing on math.  This suggests that socst is a potential correlate of missingness (Enders, 2010) and may help us satisfy the MAR assumption for multiple imputation by including it in our imputation model.

Example 1: MI using multivariate normal distribution (MVN):

When choosing to impute one or many variables, one of the first decisions you will make is the type of distribution under which you want to impute your variable(s). One method available in SAS uses Markov Chain Monte Carlo (MCMC) which assumes that all the variables in the imputation model have a joint multivariate normal distribution. This is probably the most common parametric approach for multiple imputation. The specific algorithm used is called the data augmentation (DA) algorithm, which belongs to the family of MCMC procedures. The algorithm fills in missing data by drawing from a conditional distribution, in this case a multivariate normal, of the missing data given the observed data. In most cases, simulation studies have shown that assuming a MVN distribution leads to reliable estimates even when the normality assumption is violated given a sufficient sample size (Demirtas et al., 2008; KJ Lee, 2010). However, biased estimates have been observed when the sample size is relatively small and the fraction of missing information is high.

Note: Since we are using a multivariate normal distribution for imputation, decimal and negative values are possible. These values are not a problem for estimation; however, we will need to create dummy variables for the nominal categorical variables so the parameter estimates for each level can be interpreted.

1. Imputation Phase:

Imputation in SAS requires 3 procedures. The first is proc mi where the user specifies the imputation model to be used and the number of imputed datasets to be created. The second procedure runs the analytic model of interest (here it is a linear regression using proc glm) within each of the imputed datasets. The third step runs a procedure call proc mianalyze which combines all the estimates (coefficients and standard errors) across all the imputed datasets and outputs one set of parameter estimates for the model of interest.

proc mi data= new nimpute=10 out=mi_mvn seed=54321;
var socst science write read female math progcat1 progcat2;
run;

On the proc mi procedure line we can use the nimpute option to specify the number of imputations to be performed. The imputed datasets will be outputted using the out=  option, and stored appended or “stacked” together in a dataset called “mi_mvn”. An indicator variables called _imputation_  is automatically created by the procedure to number each new imputed dataset.  After the var statement, all the variables for the imputation model are specified including all the variables in the analytic model as well as any auxiliary variables. The option seed is not required, but since MI is designed to be a random process, setting a seed will allow you to obtain the same imputed dataset each time.

2. Analysis Phase:

TITLE " MULTIPLE IMPUTATION REGRESSION - MVN";
proc glm data = mi_mvn ;
model read = write female math progcat1 progcat2 ;
by _imputation_;
ods output ParameterEstimates=a_mvn;
run;
quit;

 

This estimates the linear regression model for each imputed dataset individually using the by statement and the indicator variable created previously. You will observe in the Results Viewer, that SAS outputs the parameter estimates for each of the 10 imputations. The output statement stores the parameter estimates from the regression model in the dataset named “a_mvn.” This dataset will be used in the next step of the process, the pooling phase.

3. Pooling Phase

 

proc mianalyze parms=a_mvn;
modeleffects intercept write female math progcat1 progcat2;
run;

 

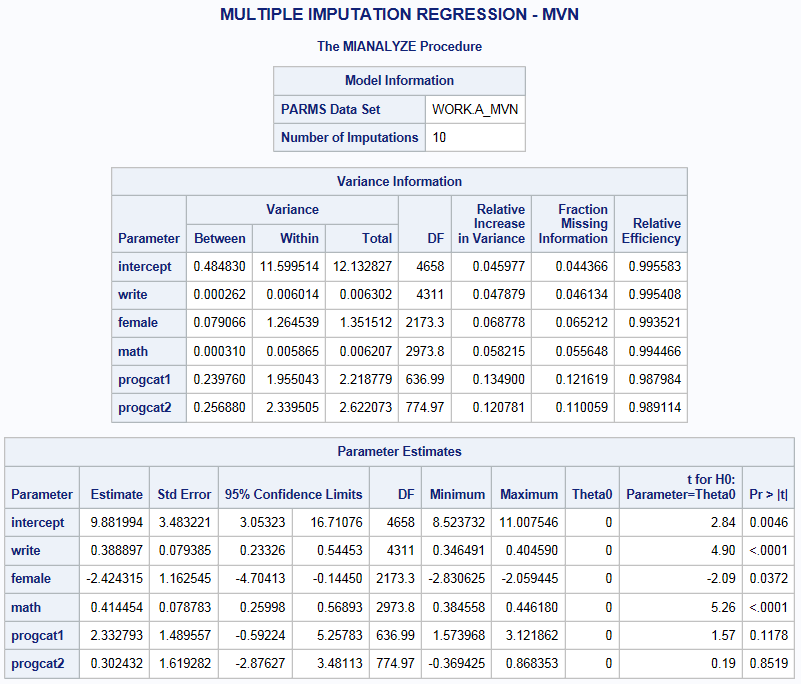
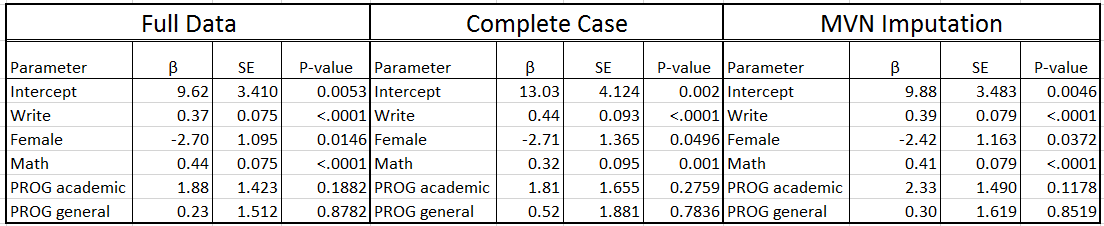
Proc mianalyze uses the dataset “a_mvn” that contains the parameter estimates and associated covariance matrices for each imputation. The variance/covariance matrix is needed to estimate the standard errors. This step combines the parameter estimates into a single set of statistics that appropriately reflect the uncertainty associated with the imputed values. The coefficients are simply just an arithmetic mean of the individual coefficients estimated for each of the 10 regression models. Averaging the parameter estimates dampens the variation thus increasing efficiency and decreasing sampling variation. Estimation of the standard error for each variable is little more complicated and will be discussed in the next section. If you compare these estimates to those from the complete data you will observe that they are, in general, quite comparable. The variables write female and math, are significant in both sets of data. You will also observe a small inflation in the standard errors, which is to be expected since the multiple imputation process is designed to build additional uncertainty into our estimates.

2. Imputation Diagnostics: 

Above the “Parameter Estimates” table in the SAS output above you will see a table called “Variance Information”. It is important to examine the output from proc mianalyze, as several pieces of the information can be used to assess how well the imputation performed. Below we discuss each piece:

1. Variance Between (V_B):
   1. This is a measure of the variability in the parameter estimates (coefficients) obtained from the 10 imputed datasets
      1. For example, if you took all 10 of the parameter estimates for write and calculated the variance this would equal V_B = 0.000262.
   2. This variability estimates the additional variation (uncertainty) that results from missing data.
2. Variance Within (V_W):
   1. This is simply the arithmetic mean of the sampling variances (SE) from each of the 10 imputed datasets.
      1. For example, if you squared the standard errors for write for all 10 imputations and then divided by 10, this would equal, this would equal V_w = 0.006014.
   2. This estimates the sampling variability that we would have expected had there been no missing data.
3. Variance Total (V_T):
   1. The primary usefulness of MI comes from how the total variance is estimated.
   2. The total variance is sum of multiple sources of variance.
   3. While regression coefficients are just averaged across imputations, Rubin’s formula (Rubin, 1987) partitions variance into “within imputation” capturing the expected uncertainty and “between imputation” capturing the estimation variability due to missing information (Graham, 2007; White et al., 2010).
   4. The total variance is the sum of 3 sources of variance. The within, the between and an additional source of sampling variance.
      1. For example, the total variance for the variable write would be calcualted like this: V_B + V_w + V_B/m = 0.000262 +0.006014 + 0.000262/10 = 0.006302
   5. The additional sampling variance is literally the variance between divided by m. This value represents the sampling error associated with the overall or average coefficient estimates. It is used as a correction factor for using a specific number of imputations.
      1. This value becomes smaller, the more imputations are conducted. The idea being that the larger the number of imputations, the more precise the parameter estimates will be.
   6. Bottom line: The main difference between multiple imputation and other single imputation methods, is in the estimation of the variances. The SE’s for each parameter estimate are the square root of it’s V_T.
4. Degrees of Freedom (DF):
   1. Unlike analysis with non-imputed data, sample size does not directly influence the estimate of DF.
   2. DF actually continues to increase as the number of imputations increase.
   3. The standard formula used to calculate DF can result in fractional estimates as well as estimates that far exceed the DF that would had resulted had the data been complete. By default the DF = infinity.
      1. Note: Starting is SAS v.8, a formula to adjust for the problem of inflated DF has been implemented (Barnard and Rubin, 1999). Use the EDF option on the proc mianalyze line to indicate to SAS what the proper adjusted DF.
   4. Bottom line:  The standard formula assumes that  the estimator has a normal distribution, i.e. a t-distribution with infinite degrees of freedom. In large samples this is not usually an issue but can be with smaller sample sizes. In that case, the corrected formula should be used (Lipsitz et al., 2002).
5. Relative Increases in Variance (RIV/RVI):
   1. Proportional increase in total sampling variance that is due to missing information ([V_B + V_B/m]/V_W).
   2. For example, the RVI for write is 0.048, this means that the estimated sampling variance for write is 4.8%  larger than its sampling variance would have been had the data on write been complete.
   3. Bottom line: Variables with large amounts of missing and/or that are weakly correlated with other variables in the imputation model will tend to have high RVI’s.
6. Fraction of Missing Information (FMI):
   1. Is directly related to RVI.
   2. Proportion of the total sampling variance that is due to missing data ([V_B+ V_B/m ]/V_T) .
   3. It’s estimated based on the percentage missing for a particular variable and how correlated this variable is with other variables in the imputation model.
   4. The interpretation is similar to an R-squared. So an FMI of 0.046 for write means that 4.6% of the total sampling variance is attributable to missing data.
   5. The accuracy of the estimate of FMI increases as the number imputation increases  because varaince estimates become more stable. This especially important in the presence of a variable(s) with a high proportion of missing information.
   6. If convergence of your imputation model is slow, examine the FMI estimates for each variables in your imputation model. A high FMI can indicate a problematic variable.
   7. Bottom line: If FMI is high for any particular variable(s) then consider increasing the number of imputations. A good rule of thumb is to have the number imputations (at least) equal the highest FMI percentage.
7. Relative Efficiency:
   1. The relative efficiency (RE) of an imputation (how well the true population parameters are estimated) is related to both the amount of missing information as well as the number (m) of imputations performed.
   2. When the amount of missing information is very low then efficiency may be achieved by only performing a few imputations (the minimum number given in most of the literature is 5). However when there is high amount of missing information, more imputations are typically necessary to achieve adequate efficiency for parameter estimates. You can obtain relatively good efficiency even with a small number of m. However, this does not mean that the standard errors will be well estimated well.
   3. More imputations are often necessary for proper standard error estimation as the variability between imputed datasets incorporate the necessary amount of uncertainty around the imputed values.
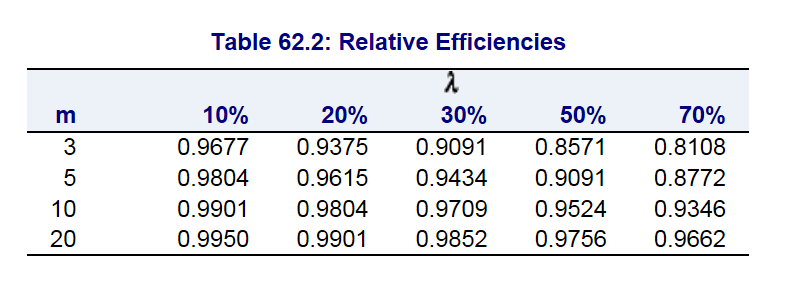
   4. The direct relationship between RE, m and the FMI is: 1/(1+FMI/m). This formula represent the RE of using m imputation versus the infinte number of imputations. To get an idea of what this looks like practically, take a look at the figure below from the SAS documentation where m is the number of imputations and λ is the FMI.
   5. Bottom line: It may appear that you can get good RE with a few imputations; however, it often takes more imputations to get good estimates of the variances than good estimates of parameters like means or regression coefficients.

After performing an imputation it is also useful to look at means, frequencies and  box plots comparing observed and imputed values to assess if the range appears reasonable. You may also want to examine plots of residuals and outliers for each imputed dataset individually. If anomalies are evident in only a small number of imputations then this indicates a problem with the imputation model (White et al, 2010).

You should also assess convergence of your imputation model. This should be done for different imputed variables, but specifically for those variables with a high proportion of missing (e.g. high FMI). Convergence of the proc mip rocedure means that DA algorithm has reached an appropriate stationary posterior distribution. Convergence for each imputed variable can be assessed using trace plots.  These plots can be requested on the mcmc statement line in the proc mi procedure.  Long-term trends in trace plots and high serial dependence are indicative of a slow convergence to stationarity. A stationary process has a mean and variance that do not change over time.

By default SAS will provide a trace plots of estimates for the means for each variable but you can also ask for these for the standard deviation as well. You can take a look at examples of good and bad trace plots in the SAS users guide section on “Assessing Markov Chain Convergence“.

proc mi data= ats.hsb_mar nimpute=10 out=mi_mvn;
mcmc plots=trace  plots=acf ;
var socst write read female math;
run;

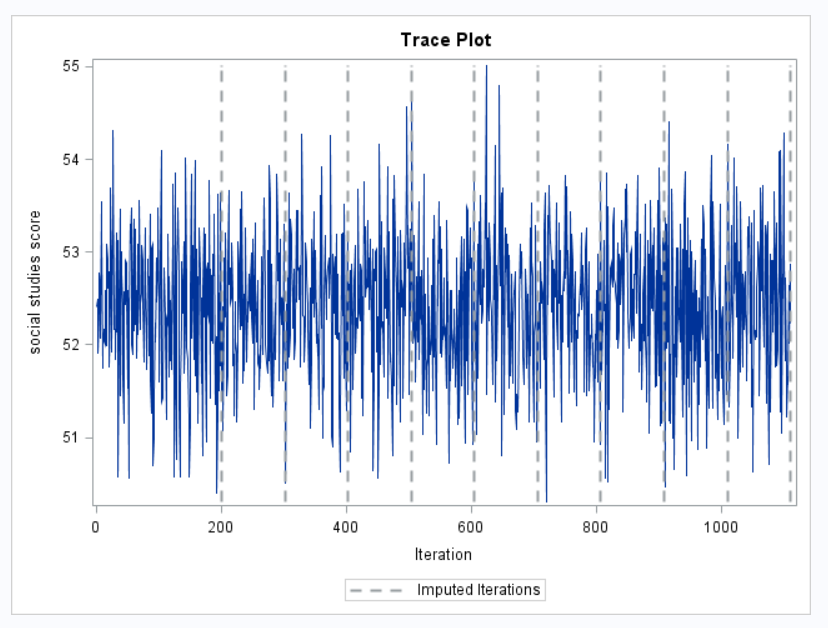
Above is an example of a trace plot for mean social studies score. There are two main things you want to note in a trace plot. First, assess whether the algorithm appeared to reach a stable posterior distribution by examining the plot to see if the mean remains relatively constant and that there appears to be an absence of any sort of trend (indicating a sufficient amount of randomness in the means between iterations). In our case, this looks to be true. Second, you want to examine the plot to see how long it takes to reach this stationary phase. In the above example it looks to happen almost immediately, indicating good convergence. The dotted lines represent at what iteration and imputed dataset is drawn. By default the burn-in period (number of iterations before the first set of imputed values is drawn) is 200. This can be increased if it appears that proper convergence is not achieved using the nbiter option on the mcmc statement. 

Another plot that is very useful for assessing convergence is the auto correlation plot also specified on the mcmc statement using plots=acf. This helps us to assess possible auto correlation of parameter values between iterations. Let’s say you noticed a trend in the mean social studies scores in the previous trace plot. You may want to assess the magnitude of the observed dependency of scores across iterations. The auto correlation plot will show you that. In the plot below, you will see that the correlation is perfect when the mcmc algorithm starts but quickly goes to near zero after a few iterations indicating almost no correlation between iterations and therefore no correlation between values in adjacent imputed datasets. By default SAS, draws an imputed dataset every 100 iterations, if correlation appears high for more than that,  you will need to increase the number of iterations between imputed datasets using  the niter option. Take a look at the SAS 9.4 proc mi documentation for more information about this and other options.

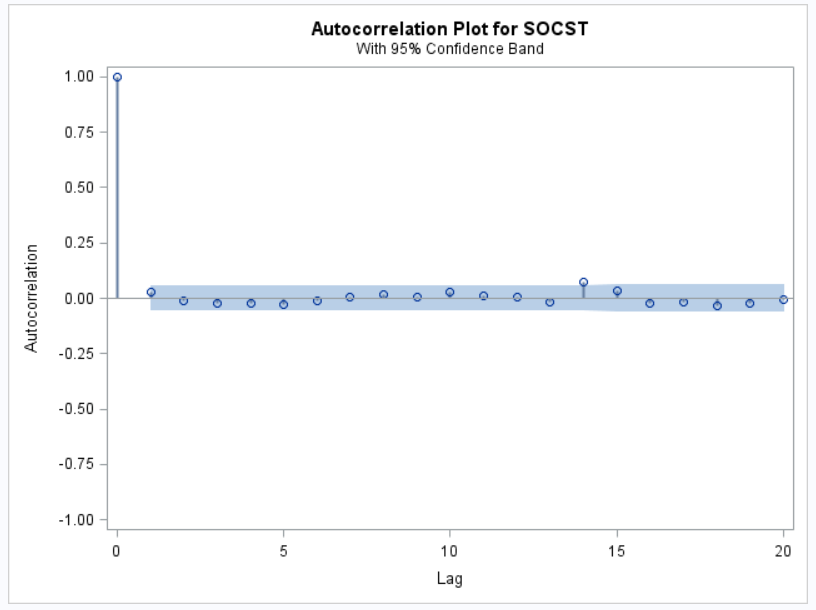
Note: The amount of time it takes to get to zero (or near zero) correlation is an indication of convergence time (Enders, 2010).

For more information on these and other diagnostic tools, please see Enders, 2010 and Rubin, 1987.

Example 2: MI using fully conditional specification (also known as imputation by chained equations/ICE or sequential generalized regression)

A second method available in SAS imputes missing variables using the fully conditional method (FCS) which does not assume a joint distribution but instead uses a separate conditional distribution for each imputed variable. This specification may be necessary if your are imputing a variable that must only take on specific values such as a binary outcome for a logistic model or count variable for a Poisson model. In simulation studies (Lee & Carlin, 2010; Van Buuren, 2007), the FCS has been show to produce estimates that are comparable to MVN method. Later we will discuss some diagnostic tools that can be used to assess if convergence was reached when using FCS.

The FCS methods available is SAS are discriminant function and logistic regression for binary/categorical variables and linear regression and predictive mean matching for continuous variables. If you do not specify a method, by default the discriminant function and regression are used. Some interesting properties of each of these options are:

1. The discriminant function method allows for the user to specify prior probabilities of group membership. In discriminant function only continuous variables can be covariates by default. To change this default use the classeffects=option.

2. The logistic regression method assumes ordering of class variables if more then two levels.

3. The default imputation method for continuous variables is regression. The regression method allows for the use of ranges and rounding for imputed values. These options are problematic and typically introduce bias (Horton et al., 2003; Allison, 2005). Take a look at the “Other Issues” section below, for further discussion on this topic.

4. The predictive mean matching method will provide imputed values that are consistent with observed values. If plausible values are necessary, this is a better choice then using bounds or rounding values produced from regression.

For more information on these methods and the options associated with them, see SAS Help and Documentation on the FCS Statement.

1. Imputation Phase

The basic set-up for conducting an imputation is shown below. The var statement includes all the variables that will be used in the imputation model. If you want to impute these variables using method different then the default  you can specify which variable(s) is to be imputed and by what method on the FCS statement. In this example we are imputing the binary variable female and the categorical variable prog using the discriminant function method. Since they are both categorical, we also list female and prog on the classstatement. Note: Because we are using the discriminant function method to impute prog we no longer need to create dummy variables. Additionally, we use the classeffects=include option so all continuous and categorical variables will be used as predictors when imputing female and prog. All the other variables on varstatement will be imputed using regression since a different distribution was not specified.

proc mi data= ats.hsb_mar nimpute=20 out=mi_fcs ;
class female prog;
fcs plots=trace(mean std); 
var socst write read female math science prog;
fcs discrim(female prog /classeffects=include) nbiter =100 ; 
run;

The ordering of variables on the var statement controls in which order variables will be imputed. With multiple imputation using FCS, a single imputation is conducted during an initial fill-in stage. After the initial stage, the variables with missing values are imputed in the order specified on the var statement. With subsequent variable being imputed using observed and imputed values from the variables that proceeded them. For more information on this see White et al., 2010. Also as in the previous proc mi example using MVN, we can also specify the number of burn-in iterations using the option nbiter.

The FCS statement also allows users to specify which variable you want to use as predictors, if no covariates are given from the imputed variable then SAS assumes that all the variables on the var statement are to be used to predict all other variables. Multiple conditional distributions can be specified in the same FCS statement. Take a look at the examples below.

This specification, imputes female and prog under a generalized logit distribution that is appropriate for non-ordered categorical variables instead of the default cumulative logit that is appropriate for ordered variables.

proc mi data= ats.hsb_mar nimpute=20 out=mi_fcs ;
class female prog; 
var socst write read female math science prog;
fcs logistic(female prog /link=glogit); 
run;

This second specification, imputes female and prog under a generalized logit distribution and uses predictive mean matching to impute math, read and write instead of the default regression method.

proc mi data= ats.hsb_mar nimpute=20 out=mi_fcs ;
class female prog; 
var socst write read female math science prog;
fcs logistic(female prog /link=glogit) regpmm(math read write); 
run;

This third specification, indicates that prog and female should be imputed using a different sets of predictors.

proc mi data= ats.hsb_mar nimpute=20 out=mi_new1;
class female prog; 
var socst write read female math science prog;
fcs logistic(female= math science/link=glogit) ;
fcs logistic(prog =math socst /link=glogit) regpmm(math read write); 
run;

2. Analysis and Pooling Phase

Once the 20 multiply imputed datasets have been created, we can run our linear regression using proc genmod. Since we imputed female and prog under a distribution appropriate for categorical outcomes, the imputed values will now be true integer values. Take a look at the results of proc freq for female and prog  in the second imputed dataset as compared to original data with missing values.

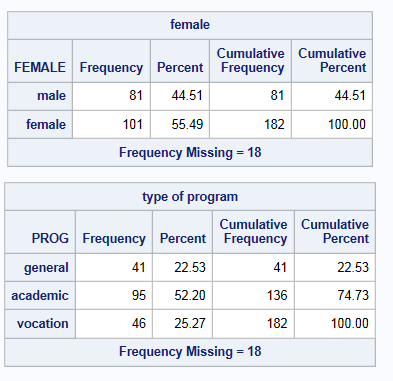
As you can see, the FCS method has imputed “real” values for our categorical variables. The variables prog and female can now be used in the class statement below and we no longer need to create dummy variables for prog.

As with the previous example using MVN, we will run our model on each imputed dataset stored in mi_fcs. We will also use an ODS Output statement to save the parameter estimates from our 20 regressions.

proc genmod data=mi_fcs;
class female prog;
model read= write female math prog /dist=normal ;
by _imputation_;
ods output ParameterEstimates=gm_fcs;
run;

Below is a proc print of what the parameter estimates in gm_fcs look like for the first two imputed datasets. ” _Imputation_ “ indicates which imputed dataset each set of parameters estimates belong to.  “Level1” indicates the levels or categories for our class variables.

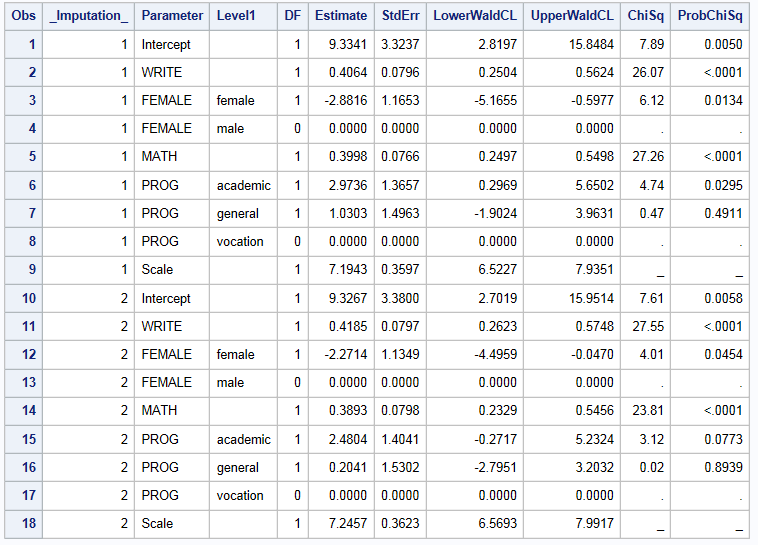
3. Pooling Phase

The mianalyze procedure will now require some additional specification in order to properly combine the parameter estimates. You can see above that the parameter estimates for variables used in our model’s class statement have estimates with 1 row for each level. Additionally, a column called “Level1” specifies the name or label associated with each category. In order from mianalyze to estimate the combined estimates appropriately for the class variables we need to add some options to the proc mianalyze line. As before the parms=refers to input SAS data set that contains parameter estimates computed from each imputed data set. However, we also need the option classvar added. This option is only appropriate when the model effects contain classification variables. Since proc genmod names the column indicator for classification “Level1” we will need to specify classvar=level.

*Note: Different procedures in SAS require different classvar options.

TITLE " MULTIPLE IMPUTATION Linear REGRESSION - FCS";
PROC MIANALYZE parms(classvar=level)=gm_fcs;
class female prog;
MODELEFFECTS INTERCEPT write female math prog;
RUN;

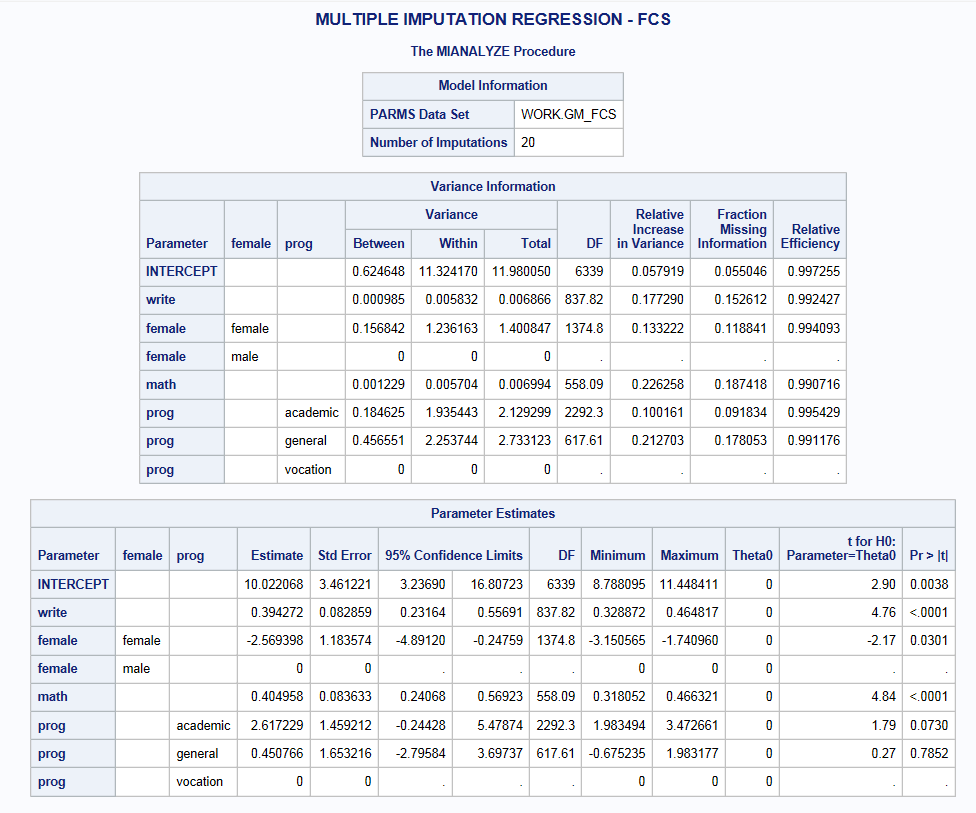
If you compare these estimates to those from the full data (below) you will see that the magnitude of the write, female, and math parameter estimates using the FCS data are very similar to the results from the full data. Additionally, the overall significance or non-significance of specific variables remains unchanged. As with the MVN model, the SE are larger due to the incorporation of uncertainty around the parameter estimates, but these SE are still smaller then we observed in the complete cases analysis.

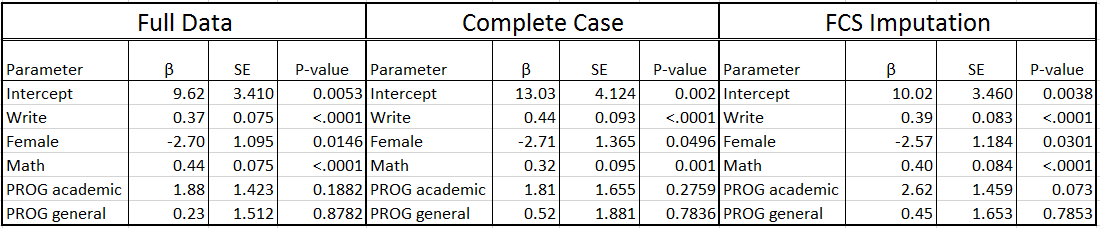
4. Imputation Diagnostics:

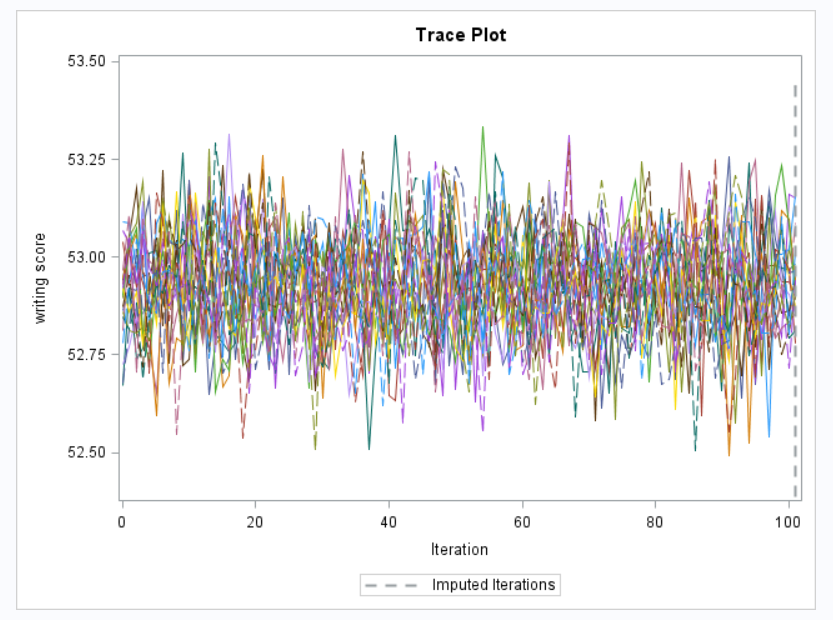
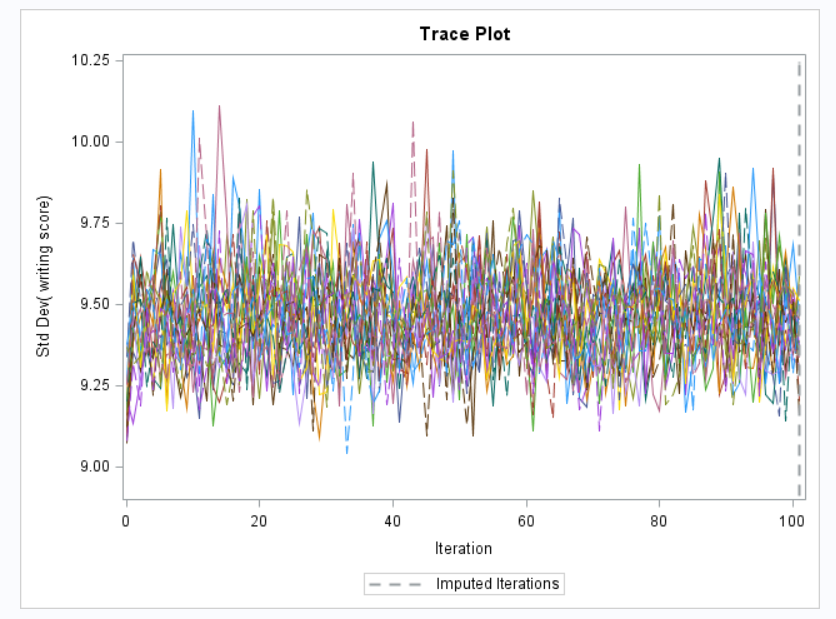
Like the previous imputation method with MVN, the FCS statement will output trace plots. These can be examined for the mean and standard deviation of each continuous variable in the imputation model. As before, the dashed vertical line indicates the final iteration where the imputation occurred. Each line represents a different imputation. So all 20 imputation chains are overlayed on top of one another. Autocorrelation plots are only available with the mcmc statement when assuming a joint multivariate normal distribution. This plot is not available when using the FCS statement.

FCS has several properties that make it an attractive alternative to the DA algorithm. First, the FCS allows each variable to be imputed using it’s own conditional distribution instead of one common multivariate distribution. This especially useful when negative or non-integer values can not be used in subsequent analyses such as imputing a binary outcome variable. Second, different imputation models can be specified for different variables. This is useful if there are particular properties of the data that need to be preserved. However, the flexibility of the approach can also cause estimation problems.  Specifying different distributions can lead to slow convergence or non-convergence of the imputation model. Additionally, issues of complete and quasi-complete separation can happen when attempting to impute a large number of categorical variables.  Overall, when attempting multiple imputation especially with FCS you should allow yourself sufficient time to build an appropriate model and time for modifications should convergence and/or estimation problems occur with your imputation model. The goal is to only have to go through this process once!

Other issues

1. Why Auxiliary variables?

So one question you may be asking yourself, is why are auxiliary variables necessary or even important.  First, they can help improve the likelihood of meeting the MAR assumption (White et al, 2011; Johnson and Young, 2011; Allison, 2012).  Remember, a variable is said to be missing at random if other variables in the dataset can be used to predict missingness on a given variable. So you want your imputation model to include all the variables you think are associated with or predict missingness in your variable in order to fulfill the assumption of MAR. Second, including auxiliaries has been shown to help yield more accurate and stable estimates and thus reduce the estimated standard errors in analytic models (Enders, 2010; Allison, 2012; von Hippel and Lynch, 2013). This is especially true in the case of missing outcome variables. Third, including these variable can also help to increase power (Reis and Judd, 2000; Enders, 2010). In general, there is almost always a benefit to adopting a more “inclusive analysis strategy” (Enders, 2010; Allison, 2012).

2. Selecting the number of imputations (m) Historically, the recommendation was for three to five MI datasets. Relatively low values of m may still be appropriate when the fraction of missing information is low and the analysis techniques are relatively simple. Recently, however, larger values of m are often being recommended. To some extent, this change in the recommended number of imputations is based on the radical increase in the computing power available to the typical researcher, making it more practical to run, create and analyze multiply imputed datasets with a larger number of imputations. Recommendations for the number of m vary. For example, five to 20 imputations for low fractions of  missing information, and as many as 50 (or more) imputations when the proportion of missing data is relatively high. Remember that estimates of coefficients stabilize at much lower values of m than estimates of variances and covariances of error terms (i.e., standard errors). Thus, in order to get appropriate estimates of these parameters, you may need to increase the m. A larger number of imputations may also allow hypothesis tests with less restrictive assumptions (i.e., that do not assume equal fractions of missing information for all coefficients). Multiple runs of m imputations are recommended to assess the stability of the parameter estimates.

Graham et al., 2007 conducted a simulation demonstrating the affect on power, efficiency and parameter estimates across different fractions of missing information as you decrease m. The authors found that:

1. Mean square error and standard error increased.

2. Power was reduced, especially when FMI is greater than 50%  and the effect size is small, even for a large number of m (20 or more).

3. Variability of the estimate of FMI  increased substantially. In general , the estimation of FMI improves with an increased m.

4. RE decreased.

Another factor to consider is the importance of reproducibility between analyses using the same data. White et al. (2010), assuming the true FMI for any variable would be less than or equal to the percentage of cases that are incomplete, uses the rule m should equal the percentage of incomplete cases. Thus if the FMI for a variable is 20% then you need 20 imputed datasets. A similar analysis by Bodner, 2008 makes a similar recommendation. White et al., 2010 also found when making this assumption, the error associated with estimating the regression coefficients, standard errors and the resulting p-values was considerably reduced and resulted in an adequate level of reproducibility.

3. Maximum, Minimum and Round

This issue often comes up in the context of using MVN to impute variables that normally have integer values or bounds. Intuitively speaking, it makes sense to round values or incorporate bounds to give “plausible” values. However, these methods has been shown to decrease efficiency and increase bias by altering the correlation or covariances between variables estimated during the imputation process. Additionally, these changes will often result in an underestimation of the uncertainly around imputed values. Remember imputed values are NOT equivalent to observed values and serve only to help estimate the covariances between variables needed for inference (Johnson and Young 2011).

Leaving the imputed values as is in the imputation model is perfectly fine for your analytic models. If plausible values are needed to perform a specific type of analysis, than you may want to use a different imputation algorithm such as FCS.

4. Common questions?

Isn’t multiple imputation just making up data?

No. This is argument can be made of the missing data methods that use a single imputed value because this value will be treated like observed data, but this is not true of multiple imputation. Unlike single imputation, multiple imputation builds into the model the uncertainty/error associated with the missing data. Therefore the process and subsequent estimation never depends on a single value. Additionally, another method for dealing the missing data, maximum likelihood produces almost identical results to multiple imputation and it does not require the missing information to be filled-in.

What is passive imputation?

Passive variables are functions of imputed variables. For example, let’s say we have a variable X with missing information but in my analytic model we will need to use X². In passive imputation we would impute X and then use those imputed values to create a quadratic term. This method is called “impute then transform” (von Hippel, 2009). While this appears to make sense, additional research (Seaman et al., 2012; Bartlett et al., 2014) has shown that using this method is actually a misspecification of your imputation model and will lead to biased parameter estimates in your analytic model. There are better ways of dealing with transformations.

How do I treat variable transformations such as logs, quadratics and interactions?

Most of the current literature on multiple imputation supports the method of treating variable transformations as “just another variable”. For example, if you know that in your subsequent analytic model you are interesting in looking at the modifying effect of Z on the association between X and Y (i.e. an interaction between X and Z). This is a property of your data that you want to be maintained in the imputation. Using something like passive imputation, where the interaction is created after you impute X and/or Z means that the filled-in values are imputed under a model assuming that Z is not a moderator of the association between X an Y. Thus, your imputation model is now misspecified.

Should I include my dependent variable (DV) in my imputation model?

Yes! An emphatic YES unless you would like to impute independent variables (IVs) assuming they are uncorrelated with your DV (Enders, 2010). Thus, causing the estimated association between you DV and IV’s to be biased toward the null (i.e. underestimated).

Additionally, using imputed values of your DV is considered perfectly acceptable when you have good auxiliary variables in your imputation model (Enders, 2010; Johnson and Young, 2011; White et al., 2010).  However, if good auxiliary variables are not available then you still INCLUDE your DV in the imputation model and then later restrict your analysis to only those observations with an observed DV value. Research has shown that imputing DV’s when auxiliary variables are not present can add unnecessary random variation into your imputed values (Allison, 2012) .

How much missing can I have and still get good estimates using MI?

Simulations have indicated that MI can perform well, under certain circumstances, even up to 50% missing observations (Allison, 2002). However, the larger the amount of missing information the higher the chance you will run into estimation problems during the imputation process and the lower the chance of meeting the MAR assumption unless it was planned missing (Johnson and Young, 2011). Additionally, as discussed further, the higher the FMI the more imputations are needed to reach good relative efficiency for effect estimates, especially standard errors.

What should I report in my methods about my imputation?

Most papers mention if they performed multiple imputation but give very few if any details of how they implemented the method. In general, a basic description should include:

1. Which statistical program was used to conduct the imputation.
2. The type of imputation algorithm used (i.e., MVN or FCS).
3. Some justification for choosing a particular imputation method.
4. The number of imputed datasets (m) created.
5. The proportion of missing observations for each imputed variable.
6. The variables used in the imputation model and why so your audience will know if you used a more inclusive strategy. This is particularly important when using auxiliary variables.

This may seem like a lot, but probably would not require more than 4-5 sentences. Enders (2010) provides some examples of write-ups for particular scenarios. Additionally, MacKinnon (2010) discusses the reporting of MI procedures in medical journals.

Main Take Always from this seminar

• Multiple Imputation is always superior to any of the single imputation methods because:
  • A single imputed value is never used
  • The variance estimates reflect the appropriate amount of uncertainty surrounding parameter estimates
• There are several decisions to be made before performing a multiple imputation including distribution, auxiliary variables and number of imputations that can affect the quality of the imputation.
• Remember that multiple imputation is not magic, and while it can help increase power it should not be expected to provide “significant” effects when other techniques like listwise deletion fail to find significant associations.
• Multiple Imputation is one tool for researchers to address the very common problem of missing data.

References

1. Allison (2002). Missing Data. Sage Publications.
2. Allison (2012).  Handling Missing Data by Maximum Likelihood. SAS Global Forum: Statistics and Data Analysis.
3. Allison (2005). Imputation of Categorical Variables with PROC MI. SUGI 30 Proceedings – Philadelphia, Pennsylvania April 10-13, 2005.
4. Barnard and Rubin (1999). Small-sample degrees of freedom with multiple imputation. Biometrika, 86(4), 948-955.
5. Bartlett et al. (2014). Multiple imputation of covariates by fully conditional specification: Accommodating the substantive model. Stat Methods Med Res.
6. Todd E. Bodner (2008).”What Improves with Increased Missing Data Imputations?”.Structural Equation Modeling: A Multidisciplinary Journal, 15:4, 651-675.
7. Demirtas et al.(2008). Plausibility of multivariate normality assumption when multiply imputing non-gaussian continuous outcomes: a simulation assessment. Jour of Stat Computation & Simulation, 78(1).
8. Enders (2010). Applied Missing Data Analysis. The Guilford Press.
9. Graham et al. (2007). How Many Imputations are Really Needed? Some Practical Clarifications of Multiple Imputation Theory. Prev Sci, 8: 206-213.
10. Horton et al. (2003) A potential for bias when rounding in multiple imputation. American Statistician. 57: 229-232.
11. Lee and Carlin (2010). Multiple Imputation for missing data: Fully Conditional Specification versus Multivariate Normal Imputation.  Am J Epidemiol, 171(5): 624-32.
12. Lipsitz et al. (2002). A Degrees-of-Freedom Approximation in Multiple Imputation.  J Statist Comput Simul, 72(4): 309-318.
13. Little, and Rubin, D.B. (2002). Statistical Analysis with Missing Data, 2^nd edition,  New York: John Wiley.
14. Johnson and Young (2011). Towards Best Practices in analyzing Datasets with Missing Data: Comparisons and Recommendations. Journal of Marriage and Family, 73(5): 926-45.
15. Mackinnon (2010). The use and reporting of multiple imputation in medical research – a review.J Intern Med, 268: 586–593.
16. Editors: Harry T. Reis, Charles M. Judd (2000). Handbook of Research Methods in Social and Personality Psychology.
17. Rubin (1976). Inference and Missing Data. Biometrika 63 (3), 581-592.
18. Rubin (1987). Multiple Imputation for Nonresponse in Surveys. J. Wiley & Sons, New York.
19. Seaman et al. (2012). Multiple Imputation of missing covariates with non-linear effects: an evaluation of statistical methods. BMC Medical Research Methodology, 12(46).
20. Schafer and Graham (2002) Missing data: our view of the state of the art. Psychol Methods, 7(2):147-77
21. van Buuren (2007). Multiple imputation of discrete and continuous data by fully conditional specification. Statistical Methods in Medical Research, 16: 219–242 .
22. von Hippel (2009). How to impute interactions, squares and other transformed variables. Sociol Methodol, 39:265-291.
23. von Hippel and Lynch (2013). Efficiency Gains from Using Auxiliary Variables in Imputation. Cornell University Library.
24. von Hippel (2013). Should a Normal Imputation Model be modified to Impute Skewed Variables. Sociological Methods & Research, 42(1):105-138.
25. White et al. (2011). Multiple imputation using chained equations: Issues and guidance for practice. Statistics in Medicine, 30(4): 377-399.
26. Young and Johnson (2011). Imputing the Missing Y’s: Implications for Survey Producers and Survey Users.  Proceedings of the AAPOR Conference Abstracts, pp. 6242–6248.