Chapter Outline
2.0 Regression Diagnostics
2.1 Unusual and Influential data
2.2 Tests on Normality of Residuals
2.3 Tests on Nonconstant Error of Variance
2.4 Tests on Multicollinearity
2.5 Tests on Nonlinearity
2.6 Model Specification
2.7 Issues of Independence
2.8 Summary
2.9 For more information
2.0 Regression Diagnostics
In our last chapter, we learned how to do ordinary linear regression with SAS, concluding with methods for examining the distribution of variables to check for non-normally distributed variables as a first look at checking assumptions in regression. Without verifying that your data have met the regression assumptions, your results may be misleading. This chapter will explore how you can use SAS to test whether your data meet the assumptions of linear regression. In particular, we will consider the following assumptions.
- Linearity – the relationships between the predictors and the outcome variable should be linear
- Normality – the errors should be normally distributed – technically normality is necessary only for the t-tests to be valid, estimation of the coefficients only requires that the errors be identically and independently distributed
- Homogeneity of variance (homoscedasticity) – the error variance should be constant
- Independence – the errors associated with one observation are not correlated with the errors of any other observation
- Errors in variables – predictor variables are measured without error (we will cover this in Chapter 4)
- Model specification – the model should be properly specified (including all relevant variables, and excluding irrelevant variables)
Additionally, there are issues that can arise during the analysis that, while strictly speaking, are not assumptions of regression, are none the less, of great concern to regression analysts.
- Influence – individual observations that exert undue influence on the coefficients
- Collinearity – predictors that are highly collinear, i.e. linearly related, can cause problems in estimating the regression coefficients.
Many graphical methods and numerical tests have been developed over the years for regression diagnostics. In this chapter, we will explore these methods and show how to verify regression assumptions and detect potential problems using SAS.
2.1 Unusual and influential data
A single observation that is substantially different from all other observations can make a large difference in the results of your regression analysis. If a single observation (or small group of observations) substantially changes your results, you would want to know about this and investigate further. There are three ways that an observation can be unusual.
Outliers: In linear regression, an outlier is an observation with large residual. In other words, it is an observation whose dependent-variable value is unusual given its values on the predictor variables. An outlier may indicate a sample peculiarity or may indicate a data entry error or other problem.
Leverage: An observation with an extreme value on a predictor variable is called a point with high leverage. Leverage is a measure of how far an observation deviates from the mean of that variable. These leverage points can have an effect on the estimate of regression coefficients.
Influence: An observation is said to be influential if removing the observation substantially changes the estimate of coefficients. Influence can be thought of as the product of leverage and outlierness.
How can we identify these three types of observations? Let’s look at an example dataset called crime. This dataset appears in Statistical Methods for Social Sciences, Third Edition by Alan Agresti and Barbara Finlay (Prentice Hall, 1997). The variables are state id (sid), state name (state), violent crimes per 100,000 people (crime), murders per 1,000,000 (murder), the percent of the population living in metropolitan areas (pctmetro), the percent of the population that is white (pctwhite), percent of population with a high school education or above (pcths), percent of population living under poverty line (poverty), and percent of population that are single parents (single). Below we use proc contents and proc means to learn more about this data file.
proc contents data="c:sasregcrime"; run;
The CONTENTS Procedure Data Set Name: c:sasregcrime Observations: 51 Member Type: DATA Variables: 9 Engine: V8 Indexes: 0 Created: 4:58 Saturday, January 9, 1960 Observation Length: 63 Last Modified: 4:58 Saturday, January 9, 1960 Deleted Observations: 0 Protection: Compressed: NO Data Set Type: Sorted: NO Label: < some output omitted to save space> -----Alphabetic List of Variables and Attributes----- # Variable Type Len Pos Label --------------------------------------------------------- 3 crime Num 4 8 violent crime rate 4 murder Num 8 12 murder rate 7 pcths Num 8 36 pct hs graduates 5 pctmetro Num 8 20 pct metropolitan 6 pctwhite Num 8 28 pct white 8 poverty Num 8 44 pct poverty 1 sid Num 8 0 9 single Num 8 52 pct single parent 2 state Char 3 60
proc means data="c:sasregcrime"; var crime murder pctmetro pctwhite pcths poverty single; run;
The MEANS Procedure Variable Label N Mean Std Dev Minimum ------------------------------------------------------------------------------- crime violent crime rate 51 612.8431373 441.1003229 82.0000000 murder murder rate 51 8.7274510 10.7175758 1.6000000 pctmetro pct metropolitan 51 67.3901959 21.9571331 24.0000000 pctwhite pct white 51 84.1156860 13.2583917 31.7999992 pcths pct hs graduates 51 76.2235293 5.5920866 64.3000031 poverty pct poverty 51 14.2588235 4.5842416 8.0000000 single pct single parent 51 11.3254902 2.1214942 8.3999996 ------------------------------------------------------------------------------- Variable Label Maximum -------------------------------------------- crime violent crime rate 2922.00 murder murder rate 78.5000000 pctmetro pct metropolitan 100.0000000 pctwhite pct white 98.5000000 pcths pct hs graduates 86.5999985 poverty pct poverty 26.3999996 single pct single parent 22.1000004 --------------------------------------------
Let’s say that we want to predict crime by pctmetro, poverty, and single. That is to say, we want to build a linear regression model between the response variable crime and the independent variables pctmetro, poverty and single. We will first look at the scatter plots of crime against each of the predictor variables before the regression analysis so we will have some ideas about potential problems. We can create a scatterplot matrix of these variables as shown below.
proc insight data="c:sasregcrime";
scatter crime pctmetro poverty single*
crime pctmetro poverty single;
run;
quit;
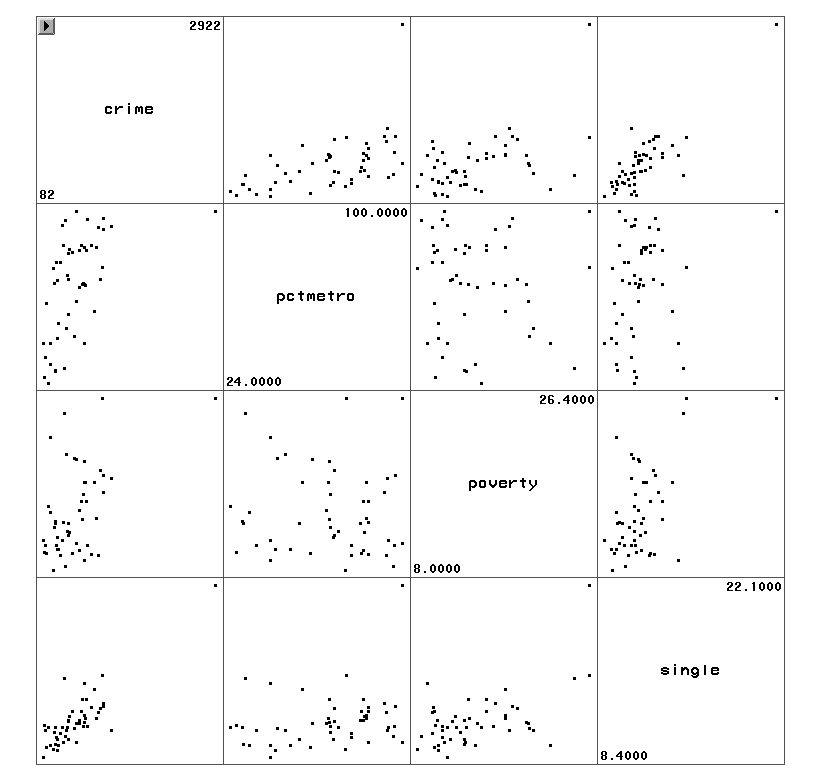
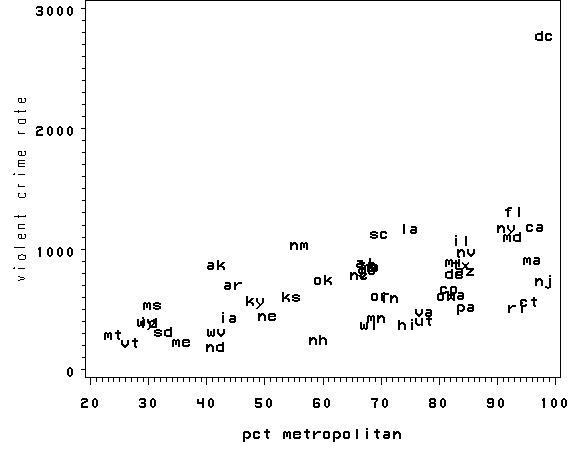
The graphs of crime with other variables show some potential problems. In every plot, we see a data point that is far away from the rest of the data points. Let’s make individual graphs of crime with pctmetro and poverty and single so we can get a better view of these scatterplots. We will add the pointlabel = ("#state") option in the symbol statement to plot the state name instead of a point.
goptions reset=all;
axis1 label=(r=0 a=90);
symbol1 pointlabel = ("#state") font=simplex value=none;
proc gplot data="c:sasregcrime";
plot crime*pctmetro=1 / vaxis=axis1;
run;
quit;
proc gplot data="c:sasregcrime"; plot crime*poverty=1 / vaxis=axis1; run; quit;
proc gplot data="c:sasregcrime"; plot crime*single=1 / vaxis=axis1; run; quit;
All the scatter plots suggest that the observation for state = dc is a point that requires extra attention since it stands out away from all of the other points. We will keep it in mind when we do our regression analysis.
Now let’s try the regression command predicting crime from pctmetro, poverty and single. We will go step-by-step to identify all the potentially unusual or influential points afterwards. We will output several statistics that we will need for the next few analyses to a dataset called crime1res, and we will explain each statistic in turn. These statistics include the studentized residual (called r), leverage (called lev), Cook’s D (called cd) and DFFITS (called dffit). We are requesting all of these statistics now so that they can be placed in a single dataset that we will use for the next several examples. Otherwise, we could have to rerun the proc reg each time we wanted a new statistic and save that statistic to another output data file.
proc reg data="c:sasregcrime";
model crime=pctmetro poverty single;
output out=crime1res(keep=sid state crime pctmetro poverty single
r lev cd dffit)
rstudent=r h=lev cookd=cd dffits=dffit;
run;
quit;
The REG Procedure
Model: MODEL1
Dependent Variable: crime violent crime rate
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 8170480 2723493 82.16 <.0001
Error 47 1557995 33149
Corrected Total 50 9728475
Root MSE 182.06817 R-Square 0.8399
Dependent Mean 612.84314 Adj R-Sq 0.8296
Coeff Var 29.70877
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 -1666.43589 147.85195 -11.27 <.0001
pctmetro pct metropolitan 1 7.82893 1.25470 6.24 <.0001
poverty pct poverty 1 17.68024 6.94093 2.55 0.0142
single pct single parent 1 132.40805 15.50322 8.54 <.0001
Let’s examine the studentized residuals as a first means for identifying outliers. We requested the studentized residuals in the above regression in the output statement and named them r. We can choose any name we like as long as it is a legal SAS variable name. Studentized residuals are a type of standardized residual that can be used to identify outliers. Let’s examine the residuals with a stem and leaf plot. We see three residuals that stick out, -3.57, 2.62 and 3.77.
proc univariate data=crime1res plots plotsize=30; var r; run;
The UNIVARIATE Procedure
Variable: r (Studentized Residual without Current Obs)
Moments
N 51 Sum Weights 51
Mean 0.0184024 Sum Observations 0.93852247
Std Deviation 1.1331258 Variance 1.28397408
Skewness 0.2243412 Kurtosis 3.05611851
Uncorrected SS 64.215975 Corrected SS 64.198704
Coeff Variation 6157.48877 Std Error Mean 0.15866935
Basic Statistical Measures
Location Variability
Mean 0.018402 Std Deviation 1.13313
Median 0.052616 Variance 1.28397
Mode . Range 7.33664
Interquartile Range 1.19867
Tests for Location: Mu0=0
Test -Statistic- -----p Value------
Student's t t 0.11598 Pr > |t| 0.9081
Sign M 0.5 Pr >= |M| 1.0000
Signed Rank S -1 Pr >= |S| 0.9926
Quantiles (Definition 5)
Quantile Estimate
100% Max 3.7658467
99% 3.7658467
95% 1.5896441
90% 1.0767182
75% Q3 0.6374511
50% Median 0.0526162
25% Q1 -0.5612179
10% -1.1293398
5% -1.6855980
1% -3.5707892
0% Min -3.5707892
Extreme Observations
------Lowest----- -----Highest-----
Value Obs Value Obs
-3.57079 25 1.15170 14
-1.83858 18 1.29348 13
-1.68560 39 1.58964 12
-1.30392 47 2.61952 9
-1.14833 35 3.76585 51
Stem Leaf # Boxplot
3 8 1 0
3
2 6 1 0
2
1 6 1 |
1 000123 6 |
0 5566788 7 +-----+
0 1111333344 10 *--+--*
-0 4433210 7 | |
-0 9976655555 10 +-----+
-1 31100 5 |
-1 87 2 |
-2
-2
-3
-3 6 1 0
----+----+----+----+
Normal Probability Plot
3.75+ *
|
| * ++++
2.25+ ++++
| ++*+
| +**** *
0.75+ +****
| *******
| ******
-0.75+ *****+
| * ****+
| * +*++
-2.25+ +++++
|+++
|
-3.75+ *
+----+----+----+----+----+----+----+----+----+----+
-2 -1 0 +1 +2
The stem and leaf display helps us see some potential outliers, but we cannot see which state (which observations) are potential outliers. Let’s sort the data on the residuals and show the 10 largest and 10 smallest residuals along with the state id and state name.
proc sort data=crime1res; by r; run; proc print data=crime1res(obs=10); run;
Obs sid state r 1 25 ms -3.57079 2 18 la -1.83858 3 39 ri -1.68560 4 47 wa -1.30392 5 35 oh -1.14833 6 48 wi -1.12934 7 6 co -1.04495 8 22 mi -1.02273 9 4 az -0.86992 10 44 ut -0.85205
proc print data=crime1res(firstobs=42 obs=51); var sid state r; run;
Obs sid state r 42 24 mo 0.82117 43 20 md 1.01299 44 29 ne 1.02887 45 40 sc 1.03034 46 16 ks 1.07672 47 14 il 1.15170 48 13 id 1.29348 49 12 ia 1.58964 50 9 fl 2.61952 51 51 dc 3.76585
We should pay attention to studentized residuals that exceed +2 or -2, and get even more concerned about residuals that exceed +2.5 or -2.5 and even yet more concerned about residuals that exceed +3 or -3. These results show that DC and MS are the most worrisome observations, followed by FL.
Let’s show all of the variables in our regression where the studentized residual exceeds +2 or -2, i.e., where the absolute value of the residual exceeds 2. We see the data for the three potential outliers we identified, namely Florida, Mississippi and Washington D.C. Looking carefully at these three observations, we couldn’t find any data entry errors, though we may want to do another regression analysis with the extreme point such as DC deleted. We will return to this issue later.
proc print data=crime1res; var r crime pctmetro poverty single; where abs(r)>2; run;
Obs r crime pctmetro poverty single 1 -3.57079 434 30.700 24.7000 14.7000 50 2.61952 1206 93.000 17.8000 10.6000 51 3.76585 2922 100.000 26.4000 22.1000
Now let’s look at the leverage’s to identify observations that will have potential great influence on regression coefficient estimates.
proc univariate data=crime1res plots plotsize=30; var lev; run;
The UNIVARIATE Procedure
Variable: lev (Leverage)
Moments
N 51 Sum Weights 51
Mean 0.07843137 Sum Observations 4
Std Deviation 0.0802847 Variance 0.00644563
Skewness 4.16424136 Kurtosis 21.514892
Uncorrected SS 0.63600716 Corrected SS 0.32228167
Coeff Variation 102.362995 Std Error Mean 0.01124211
Basic Statistical Measures
Location Variability
Mean 0.078431 Std Deviation 0.08028
Median 0.061847 Variance 0.00645
Mode . Range 0.51632
Interquartile Range 0.04766
Tests for Location: Mu0=0
Test -Statistic- -----p Value------
Student's t t 6.976572 Pr > |t| <.0001
Sign M 25.5 Pr >= |M| <.0001
Signed Rank S 663 Pr >= |S| <.0001
Quantiles (Definition 5)
Quantile Estimate
100% Max 0.5363830
99% 0.5363830
95% 0.1910120
90% 0.1362576
75% Q3 0.0851089
50% Median 0.0618474
25% Q1 0.0374442
10% 0.0292452
5% 0.0242659
1% 0.0200613
0% Min 0.0200613
Extreme Observations
-------Lowest------ ------Highest-----
Value Obs Value Obs
0.0200613 38 0.165277 2
0.0241210 6 0.180201 15
0.0242659 22 0.191012 1
0.0276638 17 0.260676 32
0.0287552 5 0.536383 51
Stem Leaf # Boxplot
52 6 1 *
50
48
46
44
42
40
38
36
34
32
30
28
26 1 1 *
24
22
20
18 01 2 0
16 5 1 0
14
12 6 1 |
10 02 2 |
8 2355515 7 +-----+
6 0123344722366 13 *--+--*
4 35567907 8 | |
2 044899112245789 15 +-----+
----+----+----+----+
Multiply Stem.Leaf by 10**-2
Normal Probability Plot
0.53+ *
|
|
|
|
0.43+
|
|
|
|
0.33+
|
|
| * +++
| ++
0.23+ +++
| ++
| ++**
| ++*
| +++
0.13+ ++ *
| +++ *
| ++ *****
| +*******
| *****
0.03+ * * ** ********+
+----+----+----+----+----+----+----+----+----+----+
-2 -1 0 +1 +2
proc sort data=crime1res; by lev; run; proc print data=crime1res (firstobs=42 obs=51); var lev state; run;
Obs lev state 42 0.09114 ky 43 0.09478 nj 44 0.09983 mt 45 0.10220 fl 46 0.13626 vt 47 0.16528 la 48 0.18020 wv 49 0.19101 ms 50 0.26068 ak 51 0.53638 dc
Generally, a point with leverage greater than (2k+2)/n should be carefully examined, where k is the number of predictors and n is the number of observations. In our example this works out to (2*3+2)/51 = .15686275, so we can do the following.
proc print data=crime1res; var crime pctmetro poverty single state; where lev > .156; run;
Obs crime pctmetro poverty single state 47 1062 75.000 26.4000 14.9000 la 48 208 41.800 22.2000 9.4000 wv 49 434 30.700 24.7000 14.7000 ms 50 761 41.800 9.1000 14.3000 ak 51 2922 100.000 26.4000 22.1000 dc
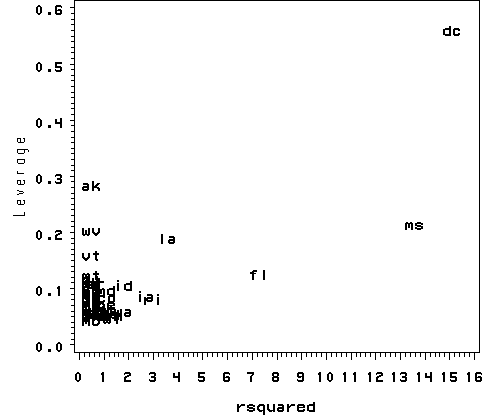
As we have seen, DC is an observation that both has a large residual and large leverage. Such points are potentially the most influential. We can make a plot that shows the leverage by the residual squared and look for observations that are jointly high on both of these measures. We can do this using a leverage versus residual-squared plot. Using residual squared instead of residual itself, the graph is restricted to the first quadrant and the relative positions of data points are preserved. This is a quick way of checking potential influential observations and outliers at the same time. Both types of points are of great concern for us.
proc sql;
create table crimeres5 as
select *, r**2/sum(r) as rsquared
from crime1res;
quit;
goptions reset=all;
axis1 label=(r=0 a=90);
symbol1 pointlabel = ("#state") font=simplex value=none;
proc gplot data=crimeres5;
plot lev*rsquared / vaxis=axis1;
run;
quit;
The point for DC catches our attention having both the highest residual squared and highest leverage, suggesting it could be very influential. The point for MS has almost as large a residual squared, but does not have the same leverage. We’ll look at those observations more carefully by listing them below.
proc print data="c:sasregcrime"; where state="dc" or state="ms"; var state crime pctmetro poverty single; run;
Obs state crime pctmetro poverty single 25 ms 434 30.700 24.7000 14.7000 51 dc 2922 100.000 26.4000 22.1000
Now let’s move on to overall measures of influence. Specifically, let’s look at Cook’s D and DFITS. These measures both combine information on the residual and leverage. Cook’s D and DFITS are very similar except that they scale differently, but they give us similar answers.
The lowest value that Cook’s D can assume is zero, and the higher the Cook’s D is, the more influential the point is. The conventional cut-off point is 4/n. We can list any observation above the cut-off point by doing the following. We do see that the Cook’s D for DC is by far the largest.
proc print data=crime1res; where cd > (4/51); var crime pctmetro poverty single state cd; run;
Obs crime pctmetro poverty single state cd 45 1206 93.000 17.8000 10.6000 fl 0.17363 47 1062 75.000 26.4000 14.9000 la 0.15926 49 434 30.700 24.7000 14.7000 ms 0.60211 51 2922 100.000 26.4000 22.1000 dc 3.20343
Now let’s take a look at DFITS. The conventional cut-off point for DFITS is 2*sqrt(k/n). DFITS can be either positive or negative, with numbers close to zero corresponding to the points with small or zero influence. As we see, DFITS also indicates that DC is, by far, the most influential observation.
proc print data=crime1res; where abs(dffit)> (2*sqrt(3/51)); var crime pctmetro poverty single state dffit; run;
Obs crime pctmetro poverty single state dffit 45 1206 93.000 17.8000 10.6000 fl 0.88382 47 1062 75.000 26.4000 14.9000 la -0.81812 49 434 30.700 24.7000 14.7000 ms -1.73510 51 2922 100.000 26.4000 22.1000 dc 4.05061
The above measures are general measures of influence. You can also consider more specific measures of influence that assess how each coefficient is changed by deleting the observation. This measure is called DFBETA and is created for each of the predictors. Apparently this is more computationally intensive than summary statistics such as Cook’s D because the more predictors a model has, the more computation it may involve. We can restrict our attention to only those predictors that we are most concerned with and to see how well behaved those predictors are. In SAS, we need to use the ods output OutStatistics statement to produce the DFBETAs for each of the predictors. The names for the new variables created are chosen by SAS automatically and begin with DFB_.
proc reg data="c:sasregcrime"; model crime=pctmetro poverty single / influence; ods output OutputStatistics=crimedfbetas; id state; run; quit;
< output omitted >
This created three variables, DFB_pctmetro, DFB_poverty and DFB_single. Let’s look at the first 5 values.
proc print data=crimedfbetas (obs=5); var state DFB_pctmetro DFB_poverty DFB_single; run;
DFB_ DFB_ DFB_ Obs state pctmetro poverty single 1 ak -0.1062 -0.1313 0.1452 2 al 0.0124 0.0553 -0.0275 3 ar -0.0687 0.1753 -0.1053 4 az -0.0948 -0.0309 0.0012 5 ca 0.0126 0.0088 -0.0036
The value for DFB_single for Alaska is 0.14, which means that by being included in the analysis (as compared to being excluded), Alaska increases the coefficient for single by 0.14 standard errors, i.e., 0.14 times the standard error for BSingle or by (0.14 * 15.5). Because the inclusion of an observation could either contribute to an increase or decrease in a regression coefficient, DFBETAs can be either positive or negative. A DFBETA value in excess of 2/sqrt(n) merits further investigation. In this example, we would be concerned about absolute values in excess of 2/sqrt(51) or 0.28.
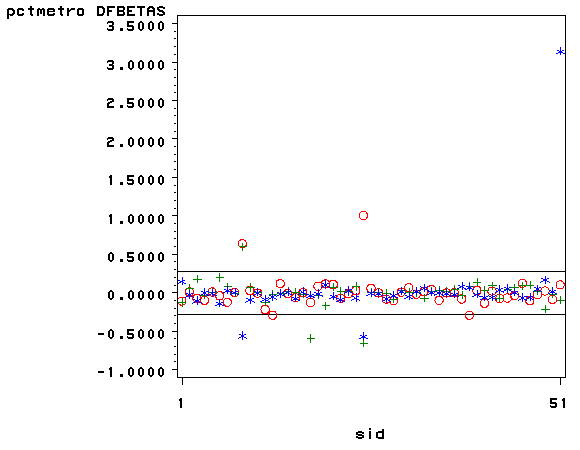
We can plot all three DFBETA values against the state id in one graph shown below. We add a line at 0.28 and -0.28 to help us see potentially troublesome observations. We see the largest value is about 3.0 for DFsingle.
data crimedfbetas1; set crimedfbetas; rename HatDiagonal=lev; run; proc sort data=crimedfbetas1; by lev; proc sort data=crime1res; by lev; run; data crimedfbetas2; merge crime1res crimedfbetas1; by lev; run; goptions reset=all; symbol1 v=circle c=red; symbol2 v=plus c=green; symbol3 v=star c=blue; axis1 order=(1 51); axis2 order=(-1 to 3.5 by .5); proc gplot data=crimedfbetas2; plot DFB_pctmetro*sid=1 DFB_poverty*sid=2 DFB_single*sid=3 / overlay haxis=axis1 vaxis=axis2 vref=-.28 .28; run; quit;
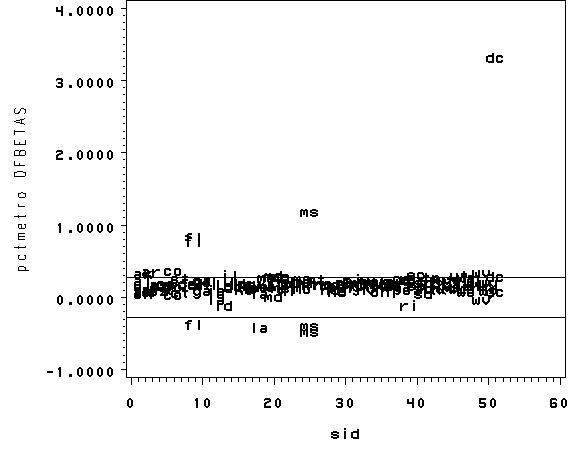
We can repeat this graph with the pointlabel = ("#state") option on the symbol1 statement to label the points. With the graph above we can identify which DFBeta is a problem, and with the graph below we can associate that observation with the state that it originates from.
goptions reset=all;
axis1 label=(r=0 a=90);
symbol1 pointlabel = ("#state") font=simplex value=none;
proc gplot data=crimedfbetas2;
plot DFB_pctmetro*sid=1 DFB_poverty*sid=2 DFB_single*sid=3
/ overlay vaxis=axis1 vref=-.28 .28;
run;
quit;
Now let’s list those observations with DFB_single larger than the cut-off value. Again, we see that DC is the most problematic observation.
proc print data=crimedfbetas2; where abs(DFB_single) > 2/sqrt(51); var DFB_single state crime pctmetro poverty single; run;
DFB_ Obs single state crime pctmetro poverty single 45 -0.5606 fl 1206 93.000 17.8000 10.6000 49 -0.5680 ms 434 30.700 24.7000 14.7000 51 3.1391 dc 2922 100.000 26.4000 22.1000
The following table summarizes the general rules of thumb we use for these measures to identify observations worthy of further investigation (where k is the number of predictors and n is the number of observations).
| Measure | Value |
| leverage | >(2k+2)/n |
| abs(rstu) | > 2 |
| Cook’s D | > 4/n |
| abs(DFITS) | > 2*sqrt(k/n) |
| abs(DFBETA) | > 2/sqrt(n) |
Washington D.C. has appeared as an outlier as well as an influential point in every analysis. Because Washington D.C. is really not a state, we can use this to justify omitting it from the analysis, saying that we really wish to just analyze states. First, let’s repeat our analysis including DC.
proc reg data="c:sasregcrime"; model crime=pctmetro poverty single; run; quit;
The REG Procedure
Model: MODEL1
Dependent Variable: crime violent crime rate
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 8170480 2723493 82.16 <.0001
Error 47 1557995 33149
Corrected Total 50 9728475
Root MSE 182.06817 R-Square 0.8399
Dependent Mean 612.84314 Adj R-Sq 0.8296
Coeff Var 29.70877
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 -1666.43589 147.85195 -11.27 <.0001
pctmetro pct metropolitan 1 7.82893 1.25470 6.24 <.0001
poverty pct poverty 1 17.68024 6.94093 2.55 0.0142
single pct single parent 1 132.40805 15.50322 8.54 <.0001
Now, let’s run the analysis omitting DC by including a where statement (here ne stands for "not equal to" but you could also use ~= to mean the same thing). As we expect, deleting DC made a large change in the coefficient for single. The coefficient for single dropped from 132.4 to 89.4. After having deleted DC, we would repeat the process we have illustrated in this section to search for any other outlying and influential observations.
proc reg data="c:sasregcrime"; model crime=pctmetro poverty single; where state ne "dc"; run; quit;
The REG Procedure
Model: MODEL1
Dependent Variable: crime violent crime rate
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 3098767 1032922 39.90 <.0001
Error 46 1190858 25888
Corrected Total 49 4289625
Root MSE 160.89817 R-Square 0.7224
Dependent Mean 566.66000 Adj R-Sq 0.7043
Coeff Var 28.39413
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 -1197.53807 180.48740 -6.64 <.0001
pctmetro pct metropolitan 1 7.71233 1.10924 6.95 <.0001
poverty pct poverty 1 18.28265 6.13596 2.98 0.0046
single pct single parent 1 89.40078 17.83621 5.01 <.0001
Summary
In this section, we explored a number of methods of identifying outliers and influential points. In a typical analysis, you would probably use only some of these methods. Generally speaking, there are two types of methods for assessing outliers: statistics such as residuals, leverage, Cook’s D and DFITS, that assess the overall impact of an observation on the regression results, and statistics such as DFBETA that assess the specific impact of an observation on the regression coefficients.
In our example, we found that DC was a point of major concern. We performed a regression with it and without it and the regression equations were very different. We can justify removing it from our analysis by reasoning that our model is to predict crime rate for states, not for metropolitan areas.
2.2 Tests for Normality of Residuals
One of the assumptions of linear regression analysis is that the residuals are normally distributed. This assumption assures that the p-values for the t-tests will be valid. As before, we will generate the residuals (called r) and predicted values (called fv) and put them in a dataset (called elem1res). We will also keep the variables api00, meals, ell and emer in that dataset.
Let’s use the elemapi2 data file we saw in Chapter 1 for these analyses. Let’s predict academic performance (api00) from percent receiving free meals (meals), percent of English language learners (ell), and percent of teachers with emergency credentials (emer).
proc reg data="c:sasregelemapi2"; model api00=meals ell emer; output out=elem1res (keep= api00 meals ell emer r fv) residual=r predicted=fv; run; quit;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 6749783 2249928 673.00 <.0001
Error 396 1323889 3343.15467
Corrected Total 399 8073672
Root MSE 57.82002 R-Square 0.8360
Dependent Mean 647.62250 Adj R-Sq 0.8348
Coeff Var 8.92804
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value
Intercept Intercept 1 886.70326 6.25976 141.65
meals pct free meals 1 -3.15919 0.14974 -21.10
ell english language learners 1 -0.90987 0.18464 -4.93
emer pct emer credential 1 -1.57350 0.29311 -5.37
Parameter Estimates
Variable Label DF Pr > |t|
Intercept Intercept 1 <.0001
meals pct free meals 1 <.0001
ell english language learners 1 <.0001
emer pct emer credential 1 <.0001
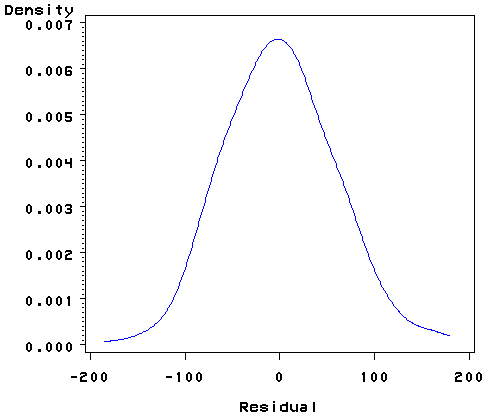
Below we use proc kde to produce a kernel density plot. kde stands for kernel density estimate. It can be thought as a histogram with narrow bins and a moving average.
proc kde data=elem1res out=den; var r; run; proc sort data=den; by r; run; goptions reset=all; symbol1 c=blue i=join v=none height=1; proc gplot data=den; plot density*r=1; run; quit;
Proc univariate will produce a normal quantile graph. qqplot plots the quantiles of a variable against the quantiles of a normal distribution. qqplotis most sensitive to non-normality near two tails. and probplot As you see below, the qqplot command shows a slight deviation from normal at the upper tail, as can be seen in the kde above. We can accept that the residuals are close to a normal distribution.
goptions reset=all; proc univariate data=elem1res normal; var r; qqplot r / normal(mu=est sigma=est); run;
The UNIVARIATE Procedure
Variable: r (Residual)
Moments
N 400 Sum Weights 400
Mean 0 Sum Observations 0
Std Deviation 57.602241 Variance 3318.01817
Skewness 0.17092898 Kurtosis 0.13532745
Uncorrected SS 1323889.25 Corrected SS 1323889.25
Coeff Variation . Std Error Mean 2.88011205
Basic Statistical Measures
Location Variability
Mean 0.00000 Std Deviation 57.60224
Median -3.65729 Variance 3318
Mode . Range 363.95555
Interquartile Range 76.47440
Tests for Location: Mu0=0
Test -Statistic- -----p Value------
Student's t t 0 Pr > |t| 1.0000
Sign M -10 Pr >= |M| 0.3421
Signed Rank S -631 Pr >= |S| 0.7855
Tests for Normality
Test --Statistic--- -----p Value------
Shapiro-Wilk W 0.996406 Pr < W 0.5101
Kolmogorov-Smirnov D 0.032676 Pr > D >0.1500
Cramer-von Mises W-Sq 0.049036 Pr > W-Sq >0.2500
Anderson-Darling A-Sq 0.340712 Pr > A-Sq >0.2500
Quantiles (Definition 5)
Quantile Estimate
100% Max 178.48224
99% 153.32833
95% 95.19177
90% 72.60901
75% Q3 36.50031
50% Median -3.65729
25% Q1 -39.97409
10% -72.36437
5% -89.25117
1% -129.60545
0% Min -185.47331
Extreme Observations
------Lowest----- -----Highest-----
Value Obs Value Obs
-185.473 226 151.684 228
-146.908 346 154.972 327
-145.515 234 161.737 188
-133.233 227 167.168 271
-125.978 259 178.482 93
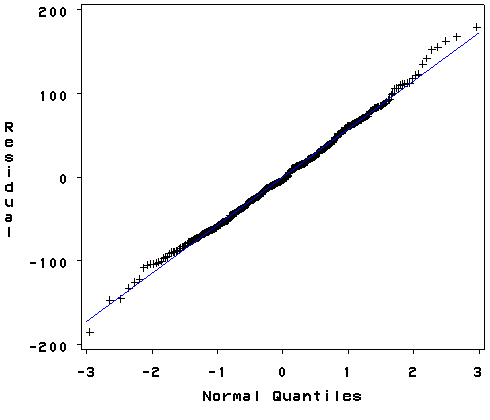
Severe outliers consist of those points that are either 3 inter-quartile-ranges below the first quartile or 3 inter-quartile-ranges above the third quartile. The presence of any severe outliers should be sufficient evidence to reject normality at a 5% significance level. Mild outliers are common in samples of any size. In our case, we don’t have any severe outliers and the distribution seems fairly symmetric. The residuals have an approximately normal distribution. (See the output of the proc univariate above.)
In the Shapiro-Wilk W test for normality, the p-value is based on the assumption that the distribution is normal. In our example, the p-value is very large (0.51), indicating that we cannot reject that r is normally distributed. (See the output of the proc univariate above.)
2.3 Tests for Heteroscedasticity
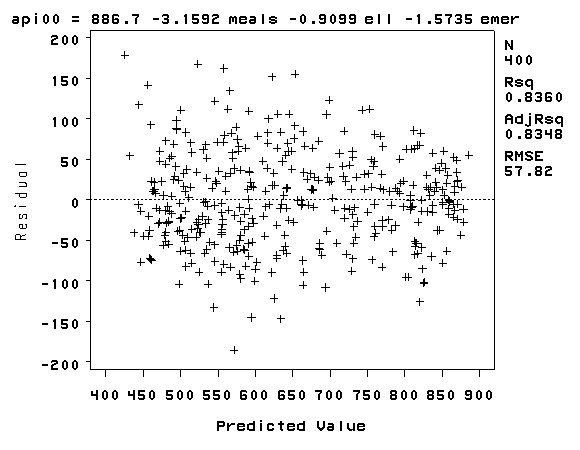
One of the main assumptions for the ordinary least squares regression is the homogeneity of variance of the residuals. If the model is well-fitted, there should be no pattern to the residuals plotted against the fitted values. If the variance of the residuals is non-constant, then the residual variance is said to be "heteroscedastic." There are graphical and non-graphical methods for detecting heteroscedasticity. A commonly used graphical method is to plot the residuals versus fitted (predicted) values. Below we use a plot statement in the proc reg. The r. and p. tell SAS to calculate the residuals (r.) and predicted values (p.) for use in the plot. We see that the pattern of the data points is getting a little narrower towards the right end, which is an indication of mild heteroscedasticity.
proc reg data='c:sasregelemapi2'; model api00 = meals ell emer; plot r.*p.; run; quit;
Now let’s look at a test for heteroscedasticity, the White test. The White test tests the null hypothesis that the variance of the residuals is homogenous. Therefore, if the p-value is very small, we would have to reject the hypothesis and accept the alternative hypothesis that the variance is not homogenous. We use the / spec option on the model statement to obtain the White test.
proc reg data='c:sasregelemapi2'; model api00 = meals ell emer / spec; run; quit;
<some output omitted to save space>
Test of First and Second
Moment Specification
DF Chi-Square Pr > ChiSq
9 22.16 0.0084
While the White test is significant, the distribution of the residuals in the residual versus fitted plot did not seem overly heteroscedastic.
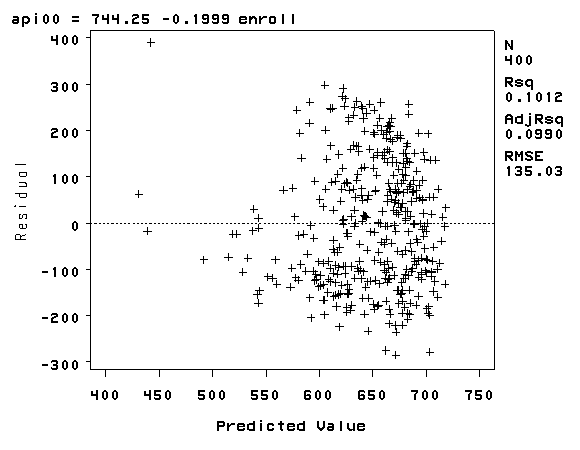
Consider another example where we use enroll as a predictor. Recall that we found enroll to be skewed to the right in Chapter 1. As you can see, this example shows much more serious heteroscedasticity.
proc reg data='c:sasregelemapi2'; model api00 = enroll; plot r.*p.; run; quit;
The REG Procedure
Model: MODEL1
Dependent Variable: api00 api 2000
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 817326 817326 44.83 <.0001
Error 398 7256346 18232
Corrected Total 399 8073672
Root MSE 135.02601 R-Square 0.1012
Dependent Mean 647.62250 Adj R-Sq 0.0990
Coeff Var 20.84949
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 744.25141 15.93308 46.71 <.0001
enroll number of students 1 -0.19987 0.02985 -6.70 <.0001
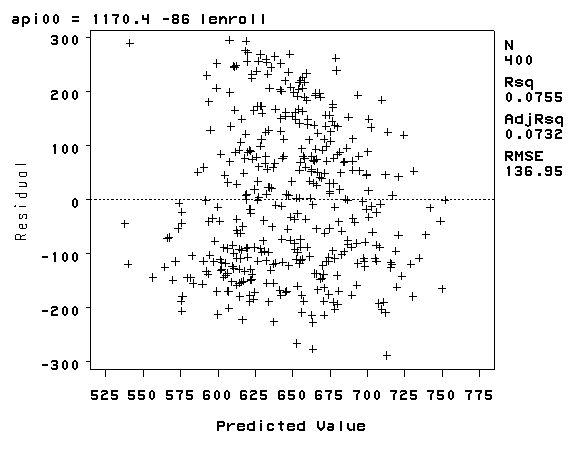
As we saw in Chapter 1, the variable enroll was skewed considerably to the right, and we found that by taking a log transformation, the transformed variable was more normally distributed. Below we transform enroll, run the regression and show the residual versus fitted plot. The distribution of the residuals is much improved. Certainly, this is not a perfect distribution of residuals, but it is much better than the distribution with the untransformed variable.
data elemapi3; set 'c:sasregelemapi2'; lenroll = log(enroll); run; proc reg data=elemapi3; model api00 = lenroll; plot r.*p.; run; quit;
The REG Procedure
Model: MODEL1
Dependent Variable: api00 api 2000
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 609460 609460 32.50 <.0001
Error 398 7464212 18754
Corrected Total 399 8073672
Root MSE 136.94634 R-Square 0.0755
Dependent Mean 647.62250 Adj R-Sq 0.0732
Coeff Var 21.14601
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 1170.42896 91.96567 12.73 <.0001
lenroll 1 -85.99991 15.08605 -5.70 <.0001
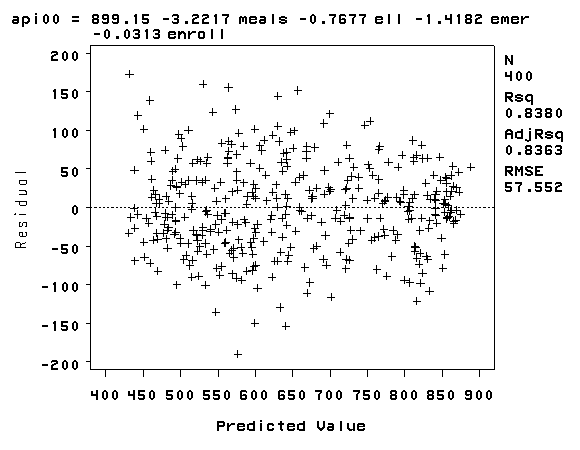
Finally, let’s revisit the model we used at the start of this section, predicting api00 from meals, ell and emer. Using this model, the distribution of the residuals looked very nice and even across the fitted values. What if we add enroll to this model? Will this automatically ruin the distribution of the residuals? Let’s add it and see.
proc reg data='c:sasregelemapi2'; model api00 = meals ell emer enroll; plot r.*p.; run; quit;
The REG Procedure
Model: MODEL1
Dependent Variable: api00 api 2000
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 4 6765344 1691336 510.63 <.0001
Error 395 1308328 3312.22265
Corrected Total 399 8073672
Root MSE 57.55191 R-Square 0.8380
Dependent Mean 647.62250 Adj R-Sq 0.8363
Coeff Var 8.88665
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value
Intercept Intercept 1 899.14659 8.47225 106.13
meals pct free meals 1 -3.22166 0.15180 -21.22
ell english language learners 1 -0.76770 0.19514 -3.93
emer pct emer credential 1 -1.41824 0.30042 -4.72
enroll number of students 1 -0.03126 0.01442 -2.17
Parameter Estimates
Variable Label DF Pr > |t|
Intercept Intercept 1 <.0001
meals pct free meals 1 <.0001
ell english language learners 1 <.0001
emer pct emer credential 1 <.0001
enroll number of students 1 0.0308
As you can see, the distribution of the residuals looks fine, even after we added the variable enroll. When we had just the variable enroll in the model, we did a log transformation to improve the distribution of the residuals, but when enroll was part of a model with other variables, the residuals looked good enough so that no transformation was needed. This illustrates how the distribution of the residuals, not the distribution of the predictor, was the guiding factor in determining whether a transformation was needed.
2.4 Tests for Collinearity
When there is a perfect linear relationship among the predictors, the estimates for a regression model cannot be uniquely computed. The term collinearity describes two variables are near perfect linear combinations of one another. When more than two variables are involved, it is often called multicollinearity, although the two terms are often used interchangeably.
The primary concern is that as the degree of multicollinearity increases, the regression model estimates of the coefficients become unstable and the standard errors for the coefficients can get wildly inflated. In this section, we will explore some SAS options used with the model statement that help to detect multicollinearity.
We can use the vif option to check for multicollinearity. vif stands for variance inflation factor. As a rule of thumb, a variable whose VIF values is greater than 10 may merit further investigation. Tolerance, defined as 1/VIF, is used by many researchers to check on the degree of collinearity. A tolerance value lower than 0.1 is comparable to a VIF of 10. It means that the variable could be considered as a linear combination of other independent variables. The tol option on the model statement gives us these values. Let’s first look at the regression we did from the last section, the regression model predicting api00 from meals, ell and emer, and use the vif and tol options with the model statement.
proc reg data='c:sasregelemapi2'; model api00 = meals ell emer / vif tol; run; quit;
The REG Procedure
Model: MODEL1
Dependent Variable: api00 api 2000
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 6749783 2249928 673.00 <.0001
Error 396 1323889 3343.15467
Corrected Total 399 8073672
Root MSE 57.82002 R-Square 0.8360
Dependent Mean 647.62250 Adj R-Sq 0.8348
Coeff Var 8.92804
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value
Intercept Intercept 1 886.70326 6.25976 141.65
meals pct free meals 1 -3.15919 0.14974 -21.10
ell english language learners 1 -0.90987 0.18464 -4.93
emer pct emer credential 1 -1.57350 0.29311 -5.37
Parameter Estimates
Variance
Variable Label DF Pr > |t| Tolerance Inflation
Intercept Intercept 1 <.0001 . 0
meals pct free meals 1 <.0001 0.36696 2.72506
ell english language learners 1 <.0001 0.39833 2.51051
emer pct emer credential 1 <.0001 0.70681 1.4148
The VIFs look fine here. Here is an example where the VIFs are more worrisome.
proc reg data='c:sasregelemapi2'; model api00 = acs_k3 avg_ed grad_sch col_grad some_col / vif tol; run; quit;
The REG Procedure
Model: MODEL1
Dependent Variable: api00 api 2000
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 5 5056269 1011254 143.79 <.0001
Error 373 2623191 7032.68421
Corrected Total 378 7679460
Root MSE 83.86110 R-Square 0.6584
Dependent Mean 647.63588 Adj R-Sq 0.6538
Coeff Var 12.94880
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 -82.60913 81.84638 -1.01 0.3135
acs_k3 avg class size k-3 1 11.45725 3.27541 3.50 0.0005
avg_ed avg parent ed 1 227.26382 37.21960 6.11 <.0001
grad_sch parent grad school 1 -2.09090 1.35229 -1.55 0.1229
col_grad parent college grad 1 -2.96783 1.01781 -2.92 0.0038
some_col parent some college 1 -0.76045 0.81097 -0.94 0.3490
Parameter Estimates
Variance
Variable Label DF Tolerance Inflation
Intercept Intercept 1 . 0
acs_k3 avg class size k-3 1 0.97187 1.02895
avg_ed avg parent ed 1 0.02295 43.57033
grad_sch parent grad school 1 0.06727 14.86459
col_grad parent college grad 1 0.06766 14.77884
some_col parent some college 1 0.24599 4.06515
In this example, the VIF and tolerance (1/VIF) values for avg_ed grad_sch and col_grad are worrisome. All of these variables measure education of the parents and the very high VIF values indicate that these variables are possibly redundant. For example, after you know grad_sch and col_grad, you probably can predict avg_ed very well. In this example, multicollinearity arises because we have put in too many variables that measure the same thing: parent education.
Let’s omit one of the parent education variables, avg_ed. Note that the VIF values in the analysis below appear much better. Also, note how the standard errors are reduced for the parent education variables, grad_sch and col_grad. This is because the high degree of collinearity caused the standard errors to be inflated. With the multicollinearity eliminated, the coefficient for grad_sch, which had been non-significant, is now significant.
proc reg data='c:sasregelemapi2'; model api00 =acs_k3 grad_sch col_grad some_col / vif tol; run; quit;
The REG Procedure
Model: MODEL1
Dependent Variable: api00 api 2000
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 4 4180144 1045036 107.12 <.0001
Error 393 3834063 9755.88497
Corrected Total 397 8014207
Root MSE 98.77188 R-Square 0.5216
Dependent Mean 648.46985 Adj R-Sq 0.5167
Coeff Var 15.23153
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 283.74462 70.32475 4.03 <.0001
acs_k3 avg class size k-3 1 11.71260 3.66487 3.20 0.0015
grad_sch parent grad school 1 5.63476 0.45820 12.30 <.0001
col_grad parent college grad 1 2.47992 0.33955 7.30 <.0001
some_col parent some college 1 2.15827 0.44388 4.86 <.0001
Parameter Estimates
Variance
Variable Label DF Tolerance Inflation
Intercept Intercept 1 . 0
acs_k3 avg class size k-3 1 0.97667 1.02389
grad_sch parent grad school 1 0.79213 1.26242
col_grad parent college grad 1 0.78273 1.27759
some_col parent some college 1 0.96670 1.03445
Let’s introduce another option regarding collinearity. The collinoint option displays several different measures of collinearity. For example, we can test for collinearity among the variables we used in the two examples above. Note that if you use the collin option, the intercept will be included in the calculation of the collinearity statistics, which is not usually what you want. The collinoint option excludes the intercept from those calculations, but it is still included in the calculation of the regression.
proc reg data='c:sasregelemapi2'; model api00 = acs_k3 avg_ed grad_sch col_grad some_col / vif tol collinoint; run; quit;
The REG Procedure
Model: MODEL1
Dependent Variable: api00 api 2000
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 5 5056269 1011254 143.79 <.0001
Error 373 2623191 7032.68421
Corrected Total 378 7679460
Root MSE 83.86110 R-Square 0.6584
Dependent Mean 647.63588 Adj R-Sq 0.6538
Coeff Var 12.94880
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 -82.60913 81.84638 -1.01 0.3135
acs_k3 avg class size k-3 1 11.45725 3.27541 3.50 0.0005
avg_ed avg parent ed 1 227.26382 37.21960 6.11 <.0001
grad_sch parent grad school 1 -2.09090 1.35229 -1.55 0.1229
col_grad parent college grad 1 -2.96783 1.01781 -2.92 0.0038
some_col parent some college 1 -0.76045 0.81097 -0.94 0.3490
Parameter Estimates
Variance
Variable Label DF Tolerance Inflation
Intercept Intercept 1 . 0
acs_k3 avg class size k-3 1 0.97187 1.02895
avg_ed avg parent ed 1 0.02295 43.57033
grad_sch parent grad school 1 0.06727 14.86459
col_grad parent college grad 1 0.06766 14.77884
some_col parent some college 1 0.24599 4.06515
Collinearity Diagnostics(intercept
adjusted)
Condition
Number Eigenvalue Index
1 2.41355 1.00000
2 1.09168 1.48690
3 0.92607 1.61438
4 0.55522 2.08495
5 0.01350 13.37294
Collinearity Diagnostics(intercept adjusted)
----------------------Proportion of Variation----------------------
Number acs_k3 avg_ed grad_sch col_grad some_col
1 0.00271 0.00389 0.00770 0.00783 0.00292
2 0.43827 6.909873E-8 0.00072293 0.00283 0.10146
3 0.47595 0.00012071 0.00517 0.00032642 0.12377
4 0.08308 0.00001556 0.05501 0.05911 0.00583
5 1.900448E-7 0.99597 0.93140 0.92990 0.76603
We now remove avg_ed and see the collinearity diagnostics improve considerably.
proc reg data='c:sasregelemapi2'; model api00 = acs_k3 grad_sch col_grad some_col / vif tol collinoint; run; quit;
The REG Procedure
Model: MODEL1
Dependent Variable: api00 api 2000
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 4 4180144 1045036 107.12 <.0001
Error 393 3834063 9755.88497
Corrected Total 397 8014207
Root MSE 98.77188 R-Square 0.5216
Dependent Mean 648.46985 Adj R-Sq 0.5167
Coeff Var 15.23153
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 283.74462 70.32475 4.03 <.0001
acs_k3 avg class size k-3 1 11.71260 3.66487 3.20 0.0015
grad_sch parent grad school 1 5.63476 0.45820 12.30 <.0001
col_grad parent college grad 1 2.47992 0.33955 7.30 <.0001
some_col parent some college 1 2.15827 0.44388 4.86 <.0001
Parameter Estimates
Variance
Variable Label DF Tolerance Inflation
Intercept Intercept 1 . 0
acs_k3 avg class size k-3 1 0.97667 1.02389
grad_sch parent grad school 1 0.79213 1.26242
col_grad parent college grad 1 0.78273 1.27759
some_col parent some college 1 0.96670 1.03445
Collinearity Diagnostics(intercept
adjusted)
Condition
Number Eigenvalue Index
1 1.50947 1.00000
2 1.04069 1.20435
3 0.92028 1.28071
4 0.52957 1.68830
Collinearity Diagnostics(intercept adjusted)
-----------------Proportion of Variation----------------
Number acs_k3 grad_sch col_grad some_col
1 0.01697 0.22473 0.22822 0.06751
2 0.62079 0.02055 0.05660 0.21947
3 0.28967 0.08150 0.00153 0.66238
4 0.07258 0.67322 0.71365 0.05064
The condition number is a commonly used index of the global instability of the regression coefficients — a large condition number, 10 or more, is an indication of instability.
2.5 Tests on Nonlinearity
When we do linear regression, we assume that the relationship between the response variable and the predictors is linear. This is the assumption of linearity. If this assumption is violated, the linear regression will try to fit a straight line to data that does not follow a straight line. Checking the linear assumption in the case of simple regression is straightforward, since we only have one predictor. All we have to do is a scatter plot between the response variable and the predictor to see if nonlinearity is present, such as a curved band or a big wave-shaped curve. For example, let us use a data file called nations.sav that has data about a number of nations around the world. Below we look at the proc contents for this file to see the variables in the file (Note that the position option tells SAS to list the variables in the order that they are in the data file.)
proc contents data='c:sasregnations' position; run;
The CONTENTS Procedure
Data Set Name: c:sasregnations Observations: 109
Member Type: DATA Variables: 15
Engine: V8 Indexes: 0
Created: 4:59 Saturday, January 9, 1960 Observation Length: 65
Last Modified: 4:59 Saturday, January 9, 1960 Deleted Observations: 0
Protection: Compressed: NO
Data Set Type: Sorted: NO
Label:
-----Engine/Host Dependent Information-----
Data Set Page Size: 8192
Number of Data Set Pages: 2
First Data Page: 1
Max Obs per Page: 125
Obs in First Data Page: 80
Number of Data Set Repairs: 0
File Name: c:sasregnations.sas7bdat
Release Created: 7.0000M0
Host Created: WIN_NT
-----Alphabetic List of Variables and Attributes-----
# Variable Type Len Pos Label
-----------------------------------------------------------------------
3 birth Num 3 8 Crude birth rate/1000 people
5 chldmort Num 3 14 Child (1-4 yr) mortality 1985
1 country Char 8 57 Country
4 death Num 3 11 Crude death rate/1000 people
9 energy Num 4 28 Per cap energy consumed, kg oil
8 food Num 4 24 Per capita daily calories 1985
10 gnpcap Num 4 32 Per capita GNP 1985
11 gnpgro Num 8 36 Annual GNP growth % 65-85
6 infmort Num 4 17 Infant (<1 yr) mortality 1985
7 life Num 3 21 Life expectancy at birth 1985
2 pop Num 8 0 1985 population in millions
13 school1 Num 4 47 Primary enrollment % age-group
14 school2 Num 3 51 Secondary enroll % age-group
15 school3 Num 3 54 Higher ed. enroll % age-group
12 urban Num 3 44 % population urban 1985
-----Variables Ordered by Position-----
# Variable Type Len Pos Label
-----------------------------------------------------------------------
1 country Char 8 57 Country
2 pop Num 8 0 1985 population in millions
3 birth Num 3 8 Crude birth rate/1000 people
4 death Num 3 11 Crude death rate/1000 people
5 chldmort Num 3 14 Child (1-4 yr) mortality 1985
6 infmort Num 4 17 Infant (<1 yr) mortality 1985
7 life Num 3 21 Life expectancy at birth 1985
8 food Num 4 24 Per capita daily calories 1985
9 energy Num 4 28 Per cap energy consumed, kg oil
10 gnpcap Num 4 32 Per capita GNP 1985
11 gnpgro Num 8 36 Annual GNP growth % 65-85
12 urban Num 3 44 % population urban 1985
13 school1 Num 4 47 Primary enrollment % age-group
14 school2 Num 3 51 Secondary enroll % age-group
15 school3 Num 3 54 Higher ed. enroll % age-group
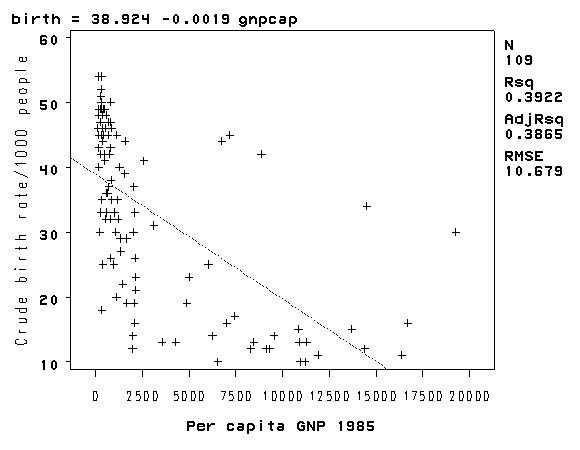
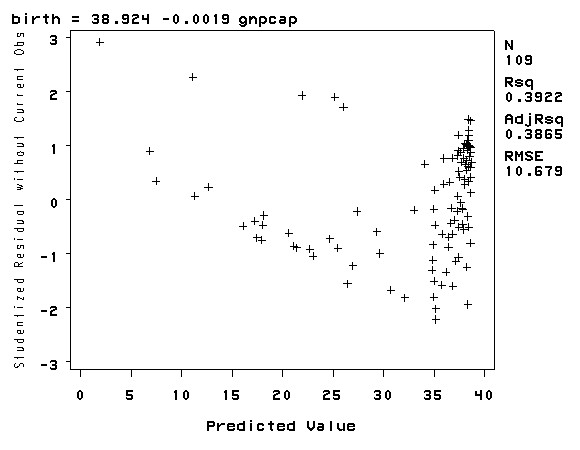
Let’s look at the relationship between GNP per capita (gnpcap) and births (birth). Below if we look at the scatterplot between gnpcap and birth, we can see that the relationship between these two variables is quite non-linear. We added a regression line to the chart, and you can see how poorly the line fits this data. Also, if we look at the residuals by predicted plot, we see that the residuals are not nearly homoscedastic, due to the non-linearity in the relationship between gnpcap and birth.
proc reg data='c:sasregnations'; model birth = gnpcap; plot rstudent.*p. / noline; plot birth*gnpcap; run; quit;
The REG Procedure
Model: MODEL1
Dependent Variable: birth Crude birth rate/1000 people
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 7873.99472 7873.99472 69.05 <.0001
Error 107 12202 114.03880
Corrected Total 108 20076
Root MSE 10.67890 R-Square 0.3922
Dependent Mean 32.78899 Adj R-Sq 0.3865
Coeff Var 32.56854
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value
Intercept Intercept 1 38.92418 1.26150 30.86
gnpcap Per capita GNP 1985 1 -0.00192 0.00023124 -8.31
Parameter Estimates
Variable Label DF Pr > |t|
Intercept Intercept 1 <.0001
gnpcap Per capita GNP 1985 1 <.0001
Now we are going to modify the above scatterplot by adding a lowess (also called "loess") smoothing line. By default, SAS will make four graphs, one for smoothing of 0.1, 0.2, 0.3 and 0.4. We show only the graph with the 0.4 smooth.
proc loess data='c:sasregnations'; model birth = gnpcap / smooth=0.1 0.2 0.3 0.4; ods output OutputStatistics=Results; run; proc sort data=results; by SmoothingParameter gnpcap; run; goptions reset=all; symbol1 v=dot i=none c=black; symbol2 v=none i=join c=blue; symbol3 v=none i=r c=red; proc gplot data=results; by SmoothingParameter; plot DepVar*gnpcap=1 pred*gnpcap=2 DepVar*gnpcap=3 / overlay; run; quit;
The LOESS Procedure
Independent Variable Scaling
Scaling applied: None
Per capita
Statistic GNP 1985
Minimum Value 110.00000
Maximum Value 19270
< some output omitted >
The LOESS Procedure
Smoothing Parameter: 0.4
Dependent Variable: api00
Fit Summary
Fit Method Interpolation
Number of Observations 400
Number of Fitting Points 17
kd Tree Bucket Size 32
Degree of Local Polynomials 1
Smoothing Parameter 0.40000
Points in Local Neighborhood 160
Residual Sum of Squares 6986406
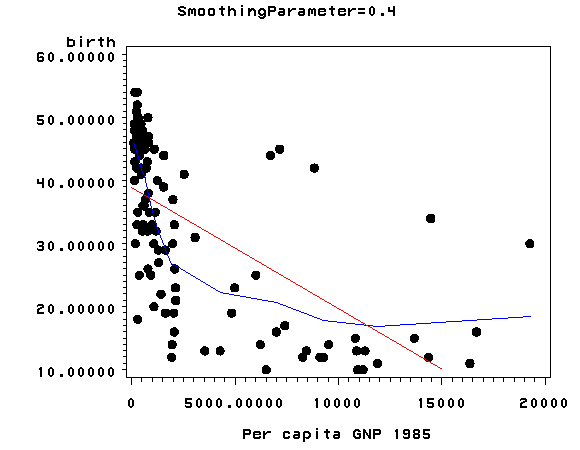
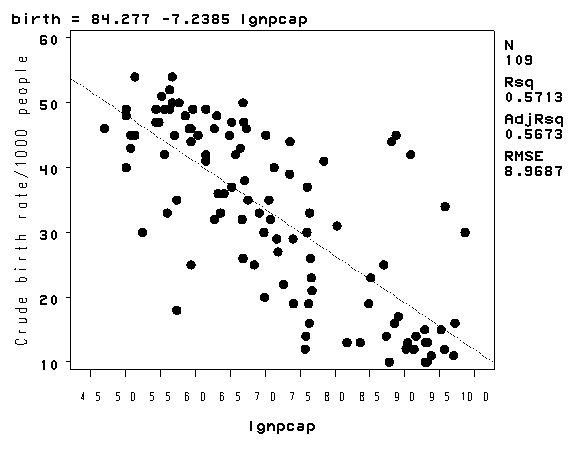
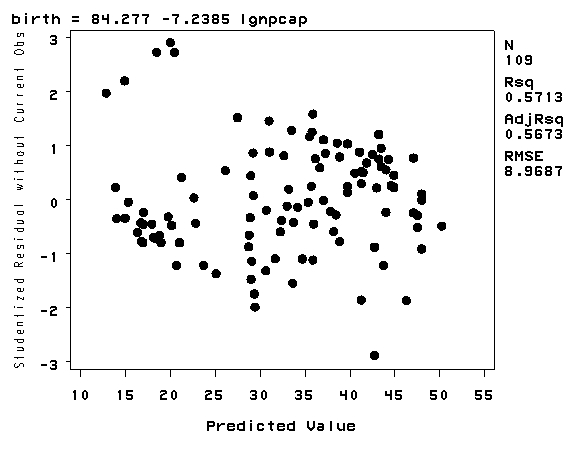
The lowess line fits much better than the OLS linear regression. In trying to see how to remedy these, we notice that the gnpcap scores are quite skewed with most values being near 0, and a handful of values of 10,000 and higher. This suggests to us that some transformation of the variable may be useful. One of the commonly used transformations is a log transformation. Let’s try it below. As you see, the scatterplot between lgnpcap and birth looks much better with the regression line going through the heart of the data. Also, the plot of the residuals by predicted values look much more reasonable.
data nations1; set 'c:sasregnations'; lgnpcap = log(gnpcap); run; proc reg data=nations1; model birth = lgnpcap; plot rstudent.*p. / noline; plot birth*lgnpcap; run; quit;
The REG Procedure
Model: MODEL1
Dependent Variable: birth Crude birth rate/1000 people
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 11469 11469 142.58 <.0001
Error 107 8606.89865 80.43831
Corrected Total 108 20076
Root MSE 8.96874 R-Square 0.5713
Dependent Mean 32.78899 Adj R-Sq 0.5673
Coeff Var 27.35290
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value
Intercept Intercept 1 84.27726 4.39668 19.17
lgnpcap 1 -7.23847 0.60619 -11.94
Parameter Estimates
Variable Label DF Pr > |t|
Intercept Intercept 1 <.0001
lgnpcap 1 <.000
This section has shown how you can use scatterplots to diagnose problems of non-linearity, both by looking at the scatterplots of the predictor and outcome variable, as well as by examining the residuals by predicted values. These examples have focused on simple regression; however, similar techniques would be useful in multiple regression. However, when using multiple regression, it would be more useful to examine partial regression plots instead of the simple scatterplots between the predictor variables and the outcome variable.
2.6 Model Specification
A model specification error can occur when one or more relevant variables are omitted from the model or one or more irrelevant variables are included in the model. If relevant variables are omitted from the model, the common variance they share with included variables may be wrongly attributed to those variables, and the error term is inflated. On the other hand, if irrelevant variables are included in the model, the common variance they share with included variables may be wrongly attributed to them. Model specification errors can substantially affect the estimate of regression coefficients.
Consider the model below. This regression suggests that as class size increases the academic performance increases. Before we publish results saying that increased class size is associated with higher academic performance, let’s check the model specification.
proc reg data='c:sasregelemapi2'; model api00 = acs_k3; output out=res1 (keep= api00 acs_k3 fv) predicted=fv; run; quit;
The REG Procedure
Model: MODEL1
Dependent Variable: api00 api 2000
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 234354 234354 11.93 0.0006
Error 396 7779853 19646
Corrected Total 397 8014207
Root MSE 140.16453 R-Square 0.0292
Dependent Mean 648.46985 Adj R-Sq 0.0268
Coeff Var 21.61466
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 308.33716 98.73085 3.12 0.0019
acs_k3 avg class size k-3 1 17.75148 5.13969 3.45 0.0006
There are a couple of methods to detect specification errors. A link test performs a model specification test for single-equation models. It is based on the idea that if a regression is properly specified, one should not be able to find any additional independent variables that are significant except by chance. To conduct this test, you need to obtain the fitted values from your regression and the squares of those values. The model is then refit using these two variables as predictors. The fitted value should be significant because it is the predicted value. One the other hand, the fitted values squared shouldn’t be significant, because if our model is specified correctly, the squared predictions should not have much of explanatory power. That is, we wouldn’t expect the fitted value squared to be a significant predictor if our model is specified correctly. So we will be looking at the p-value for the fitted value squared.
data res1sq; set res1; fv2 = fv**2; run; proc reg data=res1sq; model api00 = fv fv2; run; quit;
< some output omitted to save space >
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value
Intercept Intercept 1 3884.50651 2617.69642 1.48
fv Predicted Value of api00 1 -11.05014 8.10464 -1.36
fv2 1 0.00933 0.00627 1.49
Parameter Estimates
Variable Label DF Pr > |t|
Intercept Intercept 1 0.1386
fv Predicted Value of api00 1 0.1735
fv2 1 0.1376
Let’s try adding one more variable, meals, to the above model and then run the link test again.
proc reg data='c:sasregelemapi2'; model api00 = acs_k3 full meals; output out=res2 (keep= api00 acs_k3 full fv) predicted=fv; run; quit;
< output omitted to save space > data res2sq; set res2; fv2 = fv**2; run; proc reg data=res2sq; model api00 = fv fv2; run; quit;
< some output omitted to save space >
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value
Intercept Intercept 1 -136.51045 95.05904 -1.44
fv Predicted Value of api00 1 1.42433 0.29254 4.87
fv2 1 -0.00031721 0.00021800 -1.46
Parameter Estimates
Variable Label DF Pr > |t|
Intercept Intercept 1 0.1518
fv Predicted Value of api00 1 <.0001
fv2 1 0.1464
The link test is once again non-significant. Note that after including meals and full, the coefficient for class size is no longer significant. While acs_k3 does have a positive relationship with api00 when no other variables are in the model, when we include, and hence control for, other important variables, acs_k3 is no longer significantly related to api00 and its relationship to api00 is no longer positive.
2.7 Issues of Independence
The statement of this assumption is that the errors associated with one observation are not correlated with the errors of any other observation cover several different situations. Consider the case of collecting data from students in eight different elementary schools. It is likely that the students within each school will tend to be more like one another that students from different schools, that is, their errors are not independent. We will deal with this type of situation in Chapter 4.
Another way in which the assumption of independence can be broken is when data are collected on the same variables over time. Let’s say that we collect truancy data every semester for 12 years. In this situation it is likely that the errors for observation between adjacent semesters will be more highly correlated than for observations more separated in time. This is known as autocorrelation. When you have data that can be considered to be time-series, you should use the dw option that performs a Durbin-Watson test for correlated residuals.
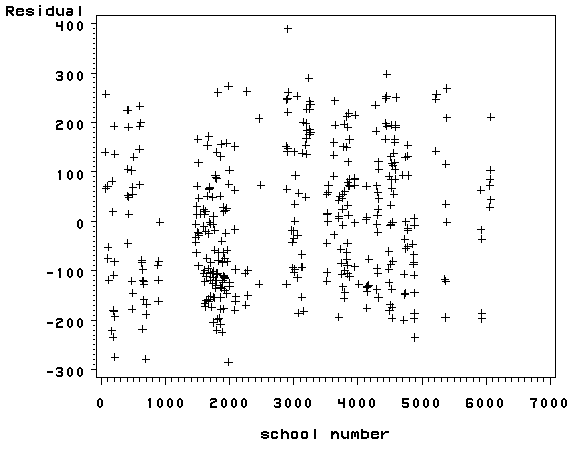
We don’t have any time-series data, so we will use the elemapi2 dataset and pretend that snum indicates the time at which the data were collected. We will sort the data on snum to order the data according to our fake time variable and then we can run the regression analysis with the dw option to request the Durbin-Watson test.
The Durbin-Watson statistic has a range from 0 to 4 with a midpoint of 2. The observed value in our example is less than 2, which is not surprising since our data are not truly time-series.
proc reg data='c:sasregelemapi2'; model api00 = enroll / dw; output out=res3 (keep = snum r) residual=r; run; quit;
The REG Procedure
Model: MODEL1
Dependent Variable: api00 api 2000
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 817326 817326 44.83 <.0001
Error 398 7256346 18232
Corrected Total 399 8073672
Root MSE 135.02601 R-Square 0.1012
Dependent Mean 647.62250 Adj R-Sq 0.0990
Coeff Var 20.84949
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 744.25141 15.93308 46.71 <.0001
enroll number of students 1 -0.19987 0.02985 -6.70 <.0001
Durbin-Watson D 1.342 Number of Observations 400 1st Order Autocorrelation 0.327
goptions reset=all; proc gplot data=res3; plot r*snum; run; quit;
2.8 Summary
In this chapter, we have used a number of tools in SAS for determining whether our data meets the regression assumptions. Below, we list the major commands we demonstrated organized according to the assumption the command was shown to test.
- Detecting Unusual and Influential Data
- scatterplots of the dependent variables versus the independent variable
- looking at the largest values of the studentized residuals, leverage, Cook’s D, DFFITS and DFBETAs
- Tests for Normality of Residuals Tests for Heteroscedasity
- kernel density plot
- quantile-quantile plots
- standardized normal probability plots
- Shapiro-Wilk W test
- scatterplot of residuals versus predicted (fitted) values
- White test
- Tests for Multicollinearity
- looking at VIF
- looking at tolerance
- Tests for Non-Linearity
- scatterplot of independent variable versus dependent variable
- Tests for Model Specification
- time series
- Durbin-Watson test
2.9 For more information
- Web Links