Chapter Outline
3.0 Regression with categorical predictors
3.1 Regression with a 0/1 variable
3.2 Regression with a 1/2 variable
3.3 Regression with a 1/2/3 variable
3.4 Regression with multiple categorical predictors
3.5 Categorical predictor with interactions
3.6 Continuous and categorical variables
3.7 Interactions of continuous by 0/1 categorical variables
3.8 Continuous and categorical variables, interaction with 1/2/3 variable
3.9 Summary
3.10 For more information
3.0 Introduction
In the previous two chapters, we have focused on regression analyses using continuous variables. However, it is possible to include categorical predictors in a regression analysis, but it requires some extra work in performing the analysis and extra work in properly interpreting the results. This chapter will illustrate how you can use SAS for including categorical predictors in your analysis and describe how to interpret the results of such analyses.
This chapter will use the elemapi2 data that you have seen in the prior chapters. We assume that you have put the data files in "c:sasreg" directory. We will focus on four variables api00, some_col, yr_rnd and mealcat, which takes meals and breaks it up into three categories. Let’s have a quick look at these variables.
proc datasets nolist;
contents data="c:sasregelemapi2" out=elemdesc noprint;
run;
proc print data=elemdesc noobs;
var name label nobs;
where name in ('api00', 'some_col', 'yr_rnd', 'mealcat');
run;
NAME LABEL NOBS api00 api 2000 400 mealcat Percentage free meals in 3 categories 400 some_col parent some college 400 yr_rnd year round school 400
So we have seen the variable label and number of valid observations for each variable. Now let’s take a look at the basic statistics of each variable. We will use proc univariate and make use of the Output Delivery System (ODS) introduced in SAS 8 to get a shorter output. ODS gives us a better control over the output a SAS procedure.
proc univariate data="c:sasregelemapi2";
ods output BasicMeasures=varinfo;
run;
proc sort data=varinfo;
by varName;
proc print data=varinfo noobs;
by varName;
where varName in ('api00', 'some_col', 'yr_rnd', 'mealcat');
run;
VarName=api00
Loc
Measure LocValue VarMeasure VarValue
Mean 647.623 Std Deviation 142.24896
Median 643.000 Variance 20235
Mode 657.000 Range 571.00000
_ Interquartile Range 239.00000
VarName=mealcat
Loc
Measure LocValue VarMeasure VarValue
Mean 2.015 Std Deviation 0.81942
Median 2.000 Variance 0.67145
Mode 3.000 Range 2.00000
_ Interquartile Range 2.00000
VarName=some_col
Loc
Measure LocValue VarMeasure VarValue
Mean 19.713 Std Deviation 11.33694
Median 19.000 Variance 128.52616
Mode 0.000 Range 67.00000
_ Interquartile Range 16.00000
VarName=yr_rnd
Loc
Measure LocValue VarMeasure VarValue
Mean 0.230 Std Deviation 0.42136
Median 0.000 Variance 0.17754
Mode 0.000 Range 1.00000
_ Interquartile Range 0
We can use proc means to obtain more or less the same type of statistics as above shown below. But we have to know the names for the statistics and we have less control over the layout of the output.
options nolabel; proc means data="c:sasregelemapi2" mean median range std var qrange; var api00 some_col yr_rnd mealcat; run;
Quartile Variable Mean Median Range Std Dev Variance Range ------------------------------------------------------------------------------- api00 647.6225000 643.0000 571.0000 142.2489610 20234.77 239 some_col 19.7125000 19.0000 67.0000 11.3369378 128.5261591 16 yr_rnd 0.2300000 0 1.0000 0.4213595 0.1775439 0 mealcat 2.0150000 2.0000 2.0000 0.8194227 0.6714536 2 --------------------------------------------------------------------------------
The variable api00 is a measure of the performance of the students. The variable some_col is a continuous variable that measures the percentage of the parents in the school who have attended college. The variable yr_rnd is a categorical variable that is coded 0 if the school is not year round, and 1 if year round. The variable meals is the percentage of students who are receiving state sponsored free meals and can be used as an indicator of poverty. This was broken into 3 categories (to make equally sized groups) creating the variable mealcat. The following macro function created for this dataset gives us codebook type information on a variable that we specify. It gives the information of the number of unique values that a variable take, which we couldn’t get from either proc univariate or proc means. This macro makes use of proc sql and has very concise output.
%macro codebook(var);
proc sql;
title "Codebook for &var";
select count(&var) label="Total of Obs",
count(distinct &var) label="Unique Values",
max(&var) label="Max",
min(&var) label="Min",
nmiss(&var) label="Coded Missing",
mean(&var) label="Mean",
std(&var) label ="Std. Dev."
from "c:sasregelemapi2";
quit;
title " ";
%mend;
options label formdlim=' ';
%codebook(api00)
%codebook(yr_rnd)
%codebook(some_col)
%codebook(mealcat)
options formdlim='';
Codebook for api00
Total Unique Coded Std.
of Obs Values Max Min Missing Mean Dev.
--------------------------------------------------------------------
400 271 940 369 0 647.6225 142.249
Codebook for yr_rnd
Total Unique Coded Std.
of Obs Values Max Min Missing Mean Dev.
--------------------------------------------------------------------
400 2 1 0 0 0.23 0.42136
Codebook for some_col
Total Unique Coded Std.
of Obs Values Max Min Missing Mean Dev.
--------------------------------------------------------------------
400 49 67 0 0 19.7125 11.33694
Codebook for mealcat
Total Unique Coded Std.
of Obs Values Max Min Missing Mean Dev.
--------------------------------------------------------------------
400 3 3 1 0 2.015 0.819423
3.1 Regression with a 0/1 variable
The simplest example of a categorical predictor in a regression analysis is a 0/1 variable, also called a dummy variable or sometimes an indicator variable. Let’s use the variable yr_rnd as an example of a dummy variable. We can include a dummy variable as a predictor in a regression analysis as shown below.
proc reg data="c:sasregelemapi2"; model api00 = yr_rnd; run; quit;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 1825001 1825001 116.24 <.0001
Error 398 6248671 15700
Corrected Total 399 8073672
Root MSE 125.30036 R-Square 0.2260
Dependent Mean 647.62250 Adj R-Sq 0.2241
Coeff Var 19.34775
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 684.53896 7.13965 95.88 <.0001
yr_rnd year round school 1 -160.50635 14.88720 -10.78 <.0001
This may seem odd at first, but this is a legitimate analysis. But what does this mean? Let’s go back to basics and write out the regression equation that this model implies.
api00 = Intercept + Byr_rnd * yr_rnd
where Intercept is the intercept (or constant) and we use Byr_rnd to represent the coefficient for variable yr_rnd. Filling in the values from the regression equation, we get
api00 = 684.539 + -160.5064 * yr_rnd
If a school is not a year-round school (i.e., yr_rnd is 0) the regression equation would simplify to
api00 = constant + 0 * Byr_rnd api00 = 684.539 + 0 * -160.5064 api00 = 684.539
If a school is a year-round school, the regression equation would simplify to
api00 = constant + 1 * Byr_rnd api00 = 684.539 + 1 * -160.5064 api00 = 524.0326
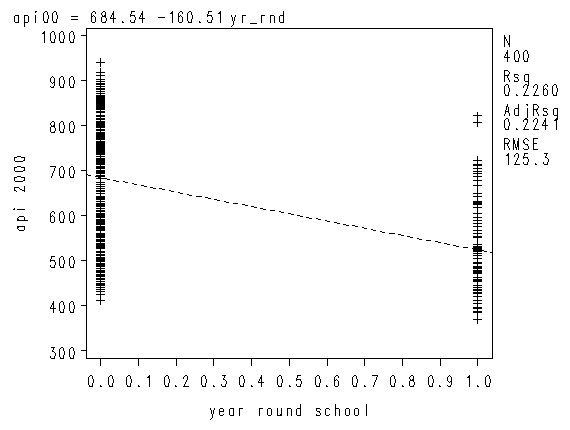
We can graph the observed values and the predicted values using the scatter command as shown below. Although yr_rnd only has two values, we can still draw a regression line showing the relationship between yr_rnd and api00. Based on the results above, we see that the predicted value for non-year round schools is 684.539 and the predicted value for the year round schools is 524.032, and the slope of the line is negative, which makes sense since the coefficient for yr_rnd was negative (-160.5064).
proc reg data="c:sasregelemapi2"; model api00 = yr_rnd; run; plot api00*yr_rnd; run; quit;
Let’s compare these predicted values to the mean api00 scores for the year-round and non-year-round students. Let’s create a format for variable yr_rnd and mealcat so we can label these categorical variables. Notice that we use the format statement in proc means below to show value labels for variable yr_rnd.
options label;
proc format library = library ;
value yr_rnd /* year round school */
0='No'
1='Yes';
value mealcat /* Percentage free meals in 3 categories */
1='0-46% free meals'
2='47-80% free meals'
3='81-100% free meals';
format yr_rnd yr_rnd.;
format mealcat mealcat.;
quit;
proc means data="c:sasregelemapi2" N mean std;
class yr_rnd ;
format yr_rnd yr_rnd.;
var api00;
run;
The MEANS Procedure
Analysis Variable : api00 api 2000
year
round N
school Obs N Mean Std Dev
----------------------------------------------------
No 308 308 684.5389610 132.1125339
Yes 92 92 524.0326087 98.9160429
----------------------------------------------------
As you see, the regression equation predicts that for a school, the value of api00 will be the mean value of the group determined by the school type.
Let’s relate these predicted values back to the regression equation. For the non-year-round schools, their mean is the same as the intercept (684.539). The coefficient for yr_rnd is the amount we need to add to get the mean for the year-round schools, i.e., we need to add -160.5064 to get 524.0326, the mean for the non year-round schools. In other words, Byr_rnd is the mean api00 score for the year-round schools minus the mean api00 score for the non year-round schools, i.e., mean(year-round) – mean(non year-round).
It may be surprising to note that this regression analysis with a single dummy variable is the same as doing a t-test comparing the mean api00 for the year-round schools with the non year-round schools (see below). You can see that the t value below is the same as the t value for yr_rnd in the regression above. This is because Byr_rnd compares the non year-rounds and non year-rounds (since the coefficient is mean(year round)-mean(non year-round)).
proc ttest data="c:sasregelemapi2" ci=none; class yr_rnd; var api00; run;
Statistics
Lower CL Upper CL
Variable yr_rnd N Mean Mean Mean Std Dev Std Err
api00 0 308 669.73 684.54 699.35 132.11 7.5278
api00 1 92 503.55 524.03 544.52 98.916 10.313
api00 Diff (1-2) 131.24 160.51 189.77 125.3 14.887
T-Tests
Variable Method Variances DF t Value Pr > |t|
api00 Pooled Equal 398 10.78 <.0001
api00 Satterthwaite Unequal 197 12.57 <.0001
Equality of Variances
Variable Method Num DF Den DF F Value Pr > F
api00 Folded F 307 91 1.78 0.0013
Since a t-test is the same as doing an anova, we can get the same results using the proc glm for anova as well.
proc glm data="c:sasregelemapi2"; class yr_rnd; model api00=yr_rnd ; run; quit;
The GLM Procedure
Dependent Variable: api00 api 2000
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 1 1825000.563 1825000.563 116.24 <.0001
Error 398 6248671.435 15700.179
Corrected Total 399 8073671.998
R-Square Coeff Var Root MSE api00 Mean
0.226043 19.34775 125.3004 647.6225
Source DF Type III SS Mean Square F Value Pr > F
yr_rnd 1 1825000.563 1825000.563 116.24 <.0001
If we square the t-value from the t-test, we get the same value as the F-value from the proc glm: 10.78^2=116.21 (with a little rounding error.)
3.2 Regression with a 1/2 variable
A categorical predictor variable does not have to be coded 0/1 to be used in a regression model. It is easier to understand and interpret the results from a model with dummy variables, but the results from a variable coded 1/2 yield essentially the same results.
Lets make a copy of the variable yr_rnd called yr_rnd2 that is coded 1/2, 1=non year-round and 2=year-round.
data elem_dummy; set "c:sasregelemapi2"; yr_rnd2=yr_rnd+1; run;
Let’s perform a regression predicting api00 from yr_rnd2.
proc reg data=elem_dummy; model api00 = yr_rnd2; run; quit;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 1825001 1825001 116.24 <.0001
Error 398 6248671 15700
Corrected Total 399 8073672
Root MSE 125.30036 R-Square 0.2260
Dependent Mean 647.62250 Adj R-Sq 0.2241
Coeff Var 19.34775
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 845.04531 19.35336 43.66 <.0001
yr_rnd2 1 -160.50635 14.88720 -10.78 <.0001
Note that the coefficient for yr_rnd is the same as yr_rnd2. So, you can see that if you code yr_rnd as 0/1 or as 1/2, the regression coefficient works out to be the same. However the intercept (Intercept) is a bit less intuitive. When we used yr_rnd, the intercept was the mean for the non year-rounds. When using yr_rnd2, the intercept is the mean for the non year-rounds minus Byr_rnd2, i.e., 684.539 – (-160.506) = 845.045
Note that you can use 0/1 or 1/2 coding and the results for the coefficient come out the same, but the interpretation of constant in the regression equation is different. It is often easier to interpret the estimates for 0/1 coding.
In summary, these results indicate that the api00 scores are significantly different for the schools depending on the type of school, year round school versus non-year round school. Non year-round schools have significantly higher API scores than year-round schools. Based on the regression results, non year-round schools have scores that are 160.5 points higher than year-round schools.
3.3 Regression with a 1/2/3 variable
3.3.1 Manually creating dummy variables
Say, that we would like to examine the relationship between the amount of poverty and api scores. We don’t have a measure of poverty, but we can use mealcat as a proxy for a measure of poverty. From the previous section, we have seen that variable mealcat has three unique values. These are the levels of percent of students on free meals. We can associate a value label to variable mealcat to make it more meaningful for us when we run SAS procedures with mealcat, for example, proc freq.
proc freq data="c:sasregelemapi2"; tables mealcat; format mealcat mealcat.; run;
Percentage free meals in 3 categories
Cumulative Cumulative
mealcat Frequency Percent Frequency Percent
-----------------------------------------------------------------------
0-46% free meals 131 32.75 131 32.75
47-80% free meals 132 33.00 263 65.75
81-100% free meals 137 34.25 400 100.00
You might be tempted to try including mealcat in a regression like this.
proc reg data="c:sasregelemapi2"; model api00 = mealcat; run; quit;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 6072528 6072528 1207.74 <.0001
Error 398 2001144 5028.00120
Corrected Total 399 8073672
Root MSE 70.90840 R-Square 0.7521
Dependent Mean 647.62250 Adj R-Sq 0.7515
Coeff Var 10.94903
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value
Intercept Intercept 1 950.98740 9.42180 100.93
mealcat Percentage free meals in 3 1 -150.55330 4.33215 -34.75
categories
Parameter Estimates
Variable Label DF Pr > |t|
Intercept Intercept 1 <.0001
mealcat Percentage free meals in 3 1 <.0001
This is looking at the linear effect of mealcat with api00, but mealcat is not an interval variable. Instead, you will want to code the variable so that all the information concerning the three levels is accounted for. In general, we need to go through a data step to create dummy variables. For example, in order to create dummy variables for mealcat, we can do the following data step.
data temp_elemapi;
set "c:sasregelemapi2";
if mealcat~=. then mealcat1=0;
if mealcat~=. then mealcat2=0;
if mealcat~=. then mealcat3=0;
if mealcat = 1 then mealcat1=1;
if mealcat = 2 then mealcat2=1;
if mealcat = 3 then mealcat3=1;
run;
Let’s run proc freq to check that our dummy coding is done correctly.
proc freq data=temp_elemapi; tables mealcat*mealcat1*mealcat2*mealcat3 /list; run;
mealcat mealcat1 mealcat2 mealcat3
-------------------------------------------
1 1 0 0
2 0 1 0
3 0 0 1
Cumulative Cumulative
Frequency Percent Frequency Percent
-------------------------------------------------
131 32.75 131 32.75
132 33.00 263 65.75
137 34.25 400 100.00
We now have created mealcat1 that is 1 if mealcat is 1, and 0 otherwise. Likewise, mealcat2 is 1 if mealcat is 2, and 0 otherwise and likewise mealcat3 was created. We can now use two of these dummy variables (mealcat2 and mealcat3) in the regression analysis.
proc reg data=temp_elemapi; model api00 = mealcat2 mealcat3; run;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 2 6094198 3047099 611.12 <.0001
Error 397 1979474 4986.08143
Corrected Total 399 8073672
Root MSE 70.61219 R-Square 0.7548
Dependent Mean 647.62250 Adj R-Sq 0.7536
Coeff Var 10.90329
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 805.71756 6.16942 130.60 <.0001
mealcat2 1 -166.32362 8.70833 -19.10 <.0001
mealcat3 1 -301.33800 8.62881 -34.92 <.0001
We can test the overall differences among the three groups by using the test command following proc reg. Notice that proc reg is an interactive procedure, so we have to issue quit command to finish it. The test result shows that the overall differences among the three groups are significant.
test mealcat2=mealcat3=0; run; quit;
Test 1 Results for Dependent Variable api00
Mean
Source DF Square F Value Pr > F
Numerator 2 3047099 611.12 <.0001
Denominator 397 4986.08143
The interpretation of the coefficients is much like that for the binary variables. Group 1 is the omitted group, so Intercept is the mean for group 1. The coefficient for mealcat2 is the mean for group 2 minus the mean of the omitted group (group 1). And the coefficient for mealcat3 is the mean of group 3 minus the mean of group 1. You can verify this by comparing the coefficients with the means of the groups.
proc means data=temp_elemapi mean std; class mealcat; var api00; run;
Analysis Variable : api00 api 2000
Percentage
free meals
in 3 N
categories Obs Mean Std Dev
---------------------------------------------------
1 131 805.7175573 65.6686642
2 132 639.3939394 82.1351295
3 137 504.3795620 62.7270149
---------------------------------------------------
Based on these results, we can say that the three groups differ in their api00 scores, and that in particular group 2 is significantly different from group1 (because mealcat2 was significant) and group 3 is significantly different from group 1 (because mealcat3 was significant).
3.3.2 More on dummy coding
In last section, we showed how to create dummy variables for mealcat by manually creating three dummy variables mealcat1, mealcat2 and mealcat3 since mealcat only has three levels. Apparently the way we created these variables is not very efficient for a categorical variables with many levels. Let’s try to make use of the array structure to make our coding more efficient.
data array_elemapi;
set "c:sasregelemapi2";
array mealdum(3) mealdum1-mealdum3;
do i = 1 to 3;
mealdum(i)=(mealcat=i);
end;
drop i;
run;
We declare an array mealdum of size 3 with each individual named to be mealdum1 to mealdum3, since mealcat has three levels. Then we do a do loop to repeat the same action three times. (mealcat=i) is a logical statement and is evaluated to be either true (1) or false (0). We can run proc freq to check if our coding is done correctly as we did in last section.
proc freq data=array_elemapi; tables mealcat*mealdum1*mealdum2*mealdum3 /list; run;
mealcat mealdum1 mealdum2 mealdum3
-------------------------------------------
1 1 0 0
2 0 1 0
3 0 0 1
Cumulative Cumulative
Frequency Percent Frequency Percent
-------------------------------------------------
131 32.75 131 32.75
132 33.00 263 65.75
137 34.25 400 100.00
3.3.3 Using the proc glm
We can also do this analysis via ANOVA. The benefit of doing anova for our analysis is that it gives us the test of the overall effect of mealcat without needing to subsequently use the test statement as we did with the proc reg. In SAS we can use the proc glm for anova. proc glm will generate dummy variables for a categorical variable on-the-fly so we don’t have to code our categorical variable mealcat manually as we did in last section through a data step.
In our program below, we use class statement to specify that variable mealcat is a categorical variable we use the option order=freq for proc glm to order the levels of our class variable according to descending frequency count so that levels with the most observations come first in the order. Thus dummy variables for mealcat = 2 and mealcat = 3 will be used in the model as they have higher frequency counts. The solution option used in the model statement gives us the parameter estimates and the ss3 option specifies that Type III sum of squares is used for hypothesis test. We can see the anova test of the effect of mealcat is the same as the test command from the regress command.
proc glm data="c:sasregelemapi2" order=freq ; class mealcat; model api00=mealcat /solution ss3; run; quit;
Dependent Variable: api00 api 2000
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 2 6094197.670 3047098.835 611.12 <.0001
Error 397 1979474.328 4986.081
Corrected Total 399 8073671.998
R-Square Coeff Var Root MSE api00 Mean
0.754824 10.90329 70.61219 647.6225
Source DF Type III SS Mean Square F Value Pr > F
mealcat 2 6094197.670 3047098.835 611.12 <.0001
Standard
Parameter Estimate Error t Value Pr > |t|
Intercept 805.7175573 B 6.16941572 130.60 <.0001
mealcat 3 -301.3379952 B 8.62881482 -34.92 <.0001
mealcat 2 -166.3236179 B 8.70833132 -19.10 <.0001
mealcat 1 0.0000000 B . . .
NOTE: The X'X matrix has been found to be singular, and a generalized inverse
was used to solve the normal equations. Terms whose estimates are
followed by the letter 'B' are not uniquely estimable.
3.3.4 Other coding schemes
It is generally very convenient to use dummy coding but it is not the only kind of coding that can be used. As you have seen, when you use dummy coding one of the groups becomes the reference group and all of the other groups are compared to that group. This may not be the most interesting set of comparisons.
Say you want to compare group 1 with 2, and group 2 with group 3. You need to generate a coding scheme that forms these 2 comparisons. In SAS, we can first generate the corresponding coding scheme in a data step shown below and use them in the proc reg step.
We create two dummy variables, one for group 1 and the other for group 3.
data effect_elemapi;
set "c:sasregelemapi2";
if mealcat=1 then do;
mealcat1=2/3;
mealcat3=1/3;
end;
if mealcat=2 then do;
mealcat1=-1/3;
mealcat3=1/3;
end;
if mealcat=3 then do;
mealcat1=-1/3;
mealcat3=-2/3;
end;
run;
Let’s check our coding with proc freq.
proc freq data=effect_elemapi; tables mealcat*mealcat1*mealcat3 / nocum nopercent list; run;
mealcat mealcat1 mealcat3 Frequency
----------------------------------------------------
1 0.6666666667 0.3333333333 131
2 -0.333333333 0.3333333333 132
3 -0.333333333 -0.666666667 137
We can now do the regression analysis again using our new coding scheme.
proc reg data=effect_elemapi ; model api00=mealcat1 mealcat3; run; quit;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 2 6094198 3047099 611.12 <.0001
Error 397 1979474 4986.08143
Corrected Total 399 8073672
Root MSE 70.61219 R-Square 0.7548
Dependent Mean 647.62250 Adj R-Sq 0.7536
Coeff Var 10.90329
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 649.83035 3.53129 184.02 <.0001
mealcat1 1 166.32362 8.70833 19.10 <.0001
mealcat3 1 135.01438 8.61209 15.68 <.0001
If you compare the parameter estimates with the group means of mealcat you can verify that B1 (i.e. 0-46% free meals) is the mean of group 1 minus group 2, and B2 (i.e., 47-80% free meals) is the mean of group 2 minus group 3. Both of these comparisons are significant, indicating that group 1 significantly differs from group 2, and group 2 significantly differs from group 3.
proc means data=effect_elemapi mean std; class mealcat; var api00;
Analysis Variable : api00 api 2000
Percentage
free meals
in 3 N
categories Obs Mean Std Dev
---------------------------------------------------
1 131 805.7175573 65.6686642
2 132 639.3939394 82.1351295
3 137 504.3795620 62.7270149
---------------------------------------------------
And the value of the intercept term Intercept is the unweighted average of the means of the three groups, (805.71756 +639.39394 +504.37956)/3 = 649.83035.
3.4 Regression with two categorical predictors
3.4.1 Manually creating dummy variables
Previously we looked at using yr_rnd to predict api00 and we have also looked at using mealcat to predict api00. Let’s include the parameter estimates for each model below.
proc reg data=array_elemapi ; model api00= yr_rnd; run; quit;proc reg data=array_elemapi ; model api00= mealcat1 mealcat2; run; quit;
Parameter Estimates
(for model with yr_rnd)
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 684.53896 7.13965 95.88 <.0001
yr_rnd year round school 1 -160.50635 14.88720 -10.78 <.0001
Parameter Estimates
(for model with mealcat1 and mealcat2)
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 504.37956 6.03281 83.61 <.0001
mealcat1 1 301.33800 8.62881 34.92 <.0001
mealcat2 1 135.01438 8.61209 15.68 <.0001
In the first model with only yr_rnd as the only predictor, the intercept term is the mean api score for the non-year-round schools. The coefficient for yr_rnd is the difference between the year round and non-year round group. In the second model, the coefficient for mealcat1 is the difference between mealcat=1 and mealcat=3, and the coefficient for mealcat2 is the difference between mealcat=2 and mealcat=3. The intercept is the mean for the mealcat=3.
Of course, we can include both yr_rnd and mealcat together in the same model. Now the question is how to interpret the coefficients.
data array_elemapi; set "c:sasregelemapi2"; array mealdum(3) mealcat1-mealcat3; do i = 1 to 3; mealdum(i)=(mealcat=i); end; drop i; run; proc reg data=array_elemapi ; model api00= yr_rnd mealcat1 mealcat2; run; quit;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 6194144 2064715 435.02 <.0001
Error 396 1879528 4746.28206
Corrected Total 399 8073672
Root MSE 68.89327 R-Square 0.7672
Dependent Mean 647.62250 Adj R-Sq 0.7654
Coeff Var 10.63787
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 526.32996 7.58453 69.40 <.0001
yr_rnd year round school 1 -42.96006 9.36176 -4.59 <.0001
mealcat1 1 281.68318 9.44568 29.82 <.0001
mealcat2 1 117.94581 9.18891 12.84 <.0001
We can test the overall effect of mealcat with the test command, which is significant.
proc reg data=array_elemapi ; model api00= yr_rnd mealcat1 mealcat2; test mealcat1=mealcat2=0; run; quit;
Test 1 Results for Dependent Variable api00
Mean
Source DF Square F Value Pr > F
Numerator 2 2184572 460.27 <.0001
Denominator 396 4746.28206
Let’s dig below the surface and see how the coefficients relate to the predicted values. Let’s view the cells formed by crossing yr_rnd and mealcat and number the cells from cell1 to cell6.
mealcat=1 mealcat=2 mealcat=3 yr_rnd=0 cell1 cell2 cell3 yr_rnd=1 cell4 cell5 cell6
With respect to mealcat, the group mealcat=3 is the reference category, and with respect to yr_rnd the group yr_rnd=0 is the reference category. As a result, cell3 is the reference cell. The intercept is the predicted value for this cell.
The coefficient for yr_rnd is the difference between cell3 and cell6. Since this model has only main effects, it is also the difference between cell2 and cell5, or from cell1 and cell4. In other words, Byr_rnd is the amount you add to the predicted value when you go from non-year round to year round schools.
The coefficient for mealcat1 is the predicted difference between cell1 and cell3. Since this model only has main effects, it is also the predicted difference between cell4 and cell6. Likewise, Bmealcat2 is the predicted difference between cell2 and cell3, and also the predicted difference between cell5 and cell6.
So, the predicted values, in terms of the coefficients, would be
mealcat=1 mealcat=2 mealcat=3
-----------------------------------------------
yr_rnd=0 Intercept Intercept Intercept
+Bmealcat1 +Bmealcat2
-----------------------------------------------
yr_rnd=1 Intercept Intercept Intercept
+Byr_rnd +Byr_rnd +Byr_rnd
+Bmealcat1 +Bmealcat2
We should note that if you computed the predicted values for each cell, they would not exactly match the means in the six cells. The predicted means would be close to the observed means in the cells, but not exactly the same. This is because our model only has main effects and assumes that the difference between cell1 and cell4 is exactly the same as the difference between cells 2 and 5 which is the same as the difference between cells 3 and 5. Since the observed values don’t follow this pattern, there is some discrepancy between the predicted means and observed means.
3.4.2 Using the proc glm
We can run the same analysis using the proc glm without manually coding the dummy variables.
proc glm data="c:sasregelemapi2"; class mealcat; model api00=yr_rnd mealcat /ss3; run; quit;
Sum of Source DF Squares Mean Square F Value Pr > F Model 3 6194144.303 2064714.768 435.02 <.0001 Error 396 1879527.694 4746.282 Corrected Total 399 8073671.998 R-Square Coeff Var Root MSE api00 Mean 0.767203 10.63787 68.89327 647.6225 Source DF Type III SS Mean Square F Value Pr > F yr_rnd 1 99946.633 99946.633 21.06 <.0001 mealcat 2 4369143.740 2184571.870 460.27 <.0001
Note that we get the same information that we do from manually coding the dummy variables and and using proc reg followed by the test statement shown in last the previous section. The proc glm doing anova automatically provides the information provided by the test statement. If we like, we can also request the parameter estimates by adding the option solution after the model statement.
proc glm data="c:sasregelemapi2"; class mealcat; model api00=yr_rnd mealcat /solution ss3; run; quit;
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 3 6194144.303 2064714.768 435.02 <.0001
Error 396 1879527.694 4746.282
Corrected Total 399 8073671.998
R-Square Coeff Var Root MSE api00 Mean
0.767203 10.63787 68.89327 647.6225
Source DF Type III SS Mean Square F Value Pr > F
yr_rnd 1 99946.633 99946.633 21.06 <.0001
mealcat 2 4369143.740 2184571.870 460.27 <.0001
Standard
Parameter Estimate Error t Value Pr > |t|
Intercept 526.3299568 B 7.58453252 69.40 <.0001
yr_rnd -42.9600584 9.36176101 -4.59 <.0001
mealcat 1 281.6831760 B 9.44567619 29.82 <.0001
mealcat 2 117.9458074 B 9.18891138 12.84 <.0001
mealcat 3 0.0000000 B . . .
NOTE: The X'X matrix has been found to be singular, and a generalized inverse
was used to solve the normal equations. Terms whose estimates are
followed by the letter 'B' are not uniquely estimable.
Recall we used option order=freq before in proc glm to force proc glm to order the levels of a class variable according to the order of descending frequency count. This time we simply used the default order of proc glm. The default order for an unformatted numerical variable is simply the order of its values. Therefore in our case, the natual order is 1 2 and 3. The proc glm will then drop the highest level.
In summary, these results indicate the differences between year round and non-year round schools is significant, and the differences among the three mealcat groups are significant.
3.5 Categorical predictor with interactions
3.5.1 Manually creating dummy variables
Let’s perform the same analysis that we performed above, this time let’s include the interaction of mealcat by yr_rnd. In this section we show how to do it by manually creating all the dummy variables. We use the array structure again. This time we have to declare two set of arrays, one for the dummy variables of mealcat and one for the interaction of yr_rnd and mealcat.
data mealxynd_elemapi;
set "c:sasregelemapi2";
array mealdum(3) mealcat1-mealcat3;
array mealxynd(3) mealxynd1-mealxynd3;
do i = 1 to 3;
mealdum(i)=(mealcat=i);
mealxynd(i)=mealdum(i)*yr_rnd;
end;
drop i;
run;
We can check to see if our dummy variables have been created correctly. Notice the option nopercent and nocum suppress the output on percent and cumulative percent. The option list displays two-way to n-way tables in a list format rather than as crosstabulation tables. It seems that our coding has been done correctly.
proc freq data=mealxynd_elemapi; tables yr_rnd*mealcat*mealxynd1*mealxynd2*mealxynd3 /nopercent nocum list; run;
yr_rnd mealcat mealxynd1 mealxynd2 mealxynd3 Frequency
---------------------------------------------------------------------
0 1 0 0 0 124
0 2 0 0 0 117
0 3 0 0 0 67
1 1 1 0 0 7
1 2 0 1 0 15
1 3 0 0 1 70
Now let’s add these dummy variables for interaction between yr_rnd and mealcat to our model. We can all add a test statement to test the overall interaction. The output shows that the interaction effect is not significant.
proc reg data=mealxynd_elemapi; model api00=yr_rnd mealcat1 mealcat2 mealxynd1 mealxynd2; test mealxynd1=mealxynd2=0; run; quit;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 5 6204728 1240946 261.61 <.0001
Error 394 1868944 4743.51314
Corrected Total 399 8073672
Root MSE 68.87317 R-Square 0.7685
Dependent Mean 647.62250 Adj R-Sq 0.7656
Coeff Var 10.63477
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 521.49254 8.41420 61.98 <.0001
yr_rnd year round school 1 -33.49254 11.77129 -2.85 0.0047
mealcat1 1 288.19295 10.44284 27.60 <.0001
mealcat2 1 123.78097 10.55185 11.73 <.0001
mealxynd1 1 -40.76438 29.23118 -1.39 0.1639
mealxynd2 1 -18.24763 22.25624 -0.82 0.4128
The REG Procedure
Model: MODEL1
Test 1 Results for Dependent Variable api00
Mean
Source DF Square F Value Pr > F
Numerator 2 5291.75936 1.12 0.3288
Denominator 394 4743.51314
It is important to note how the meaning of the coefficients change in the presence of these interaction terms. For example, in the prior model, with only main effects, we could interpret Byr_rnd as the difference between the year round and non year round schools. However, now that we have added the interaction term, the term Byr_rnd represents the difference between cell3 and cell6, or the difference between the year round and non-year round schools when mealcat=3 (because mealcat=3 was the omitted group). The presence of an interaction would imply that the difference between year round and non-year round schools depends on the level of mealcat. The interaction terms Bmealxynd1 and Bmealxynd2 represent the extent to which the difference between the year round/non year round schools changes when mealcat=1 and when mealcat=2 (as compared to the reference group, mealcat=3). For example the term Bmealxynd1 represents the difference between year round and non-year round for mealcat=1 versus the difference for mealcat=3. In other words, Bmealxynd1 in this design is (cell1-cell4) – (cell3-cell6), or it represents how much the effect of yr_rnd differs between mealcat=1 and mealcat=3.
Below we have shown the predicted values for the six cells in terms of the coefficients in the model. If you compare this to the main effects model, you will see that the predicted values are the same except for the addition of mealxynd1 (in cell 4) and mealxynd2 (in cell 5).
mealcat=1 mealcat=2 mealcat=3
-------------------------------------------------
yr_rnd=0 Intercept Intercept Intercept
+Bmealcat1 +Bmealcat2
-------------------------------------------------
yr_rnd=1 Intercept Intercept Intercept
+Byr_rnd +Byr_rnd +Byr_rnd
+Bmealcat1 +Bmealcat2
+Bmealxynd1 +Bmealxynd2
It can be very tricky to interpret these interaction terms if you wish to form specific comparisons. For example, if you wanted to perform a test of the simple main effect of yr_rnd when mealcat=1, i.e., comparing compare cell1 with cell4, you would want to compare Intercept+ mealcat1 versus Intercept + mealcat1 + yr_rnd + mealxynd1 and since Intercept and Imealcat1 would drop out, we would test
proc reg data=mealxynd_elemapi; model api00=yr_rnd mealcat1 mealcat2 mealxynd1 mealxynd2; test yr_rnd + mealxynd1=0; run; quit;
Test 1 Results for Dependent Variable api00
Mean
Source DF Square F Value Pr > F
Numerator 1 36536 7.70 0.0058
Denominator 394 4743.51314
This test is significant, indicating that the effect of yr_rnd is significant for the mealcat = 1 group.
As we will see, such tests can be more easily done via anova using proc glm.
3.5.2 Using anova
Constructing these interactions can be easier when using the proc glm. We can also avoid manually coding our dummy variables. As you see below, the proc glm gives us the test of the overall main effects and interactions without the need to perform subsequent test commands.
proc glm data="c:sasregelemapi2"; class mealcat; model api00=yr_rnd mealcat yr_rnd*mealcat /ss3; run; quit;
Sum of Source DF Squares Mean Square F Value Pr > F Model 5 6204727.822 1240945.564 261.61 <.0001 Error 394 1868944.176 4743.513 Corrected Total 399 8073671.998 R-Square Coeff Var Root MSE api00 Mean 0.768514 10.63477 68.87317 647.6225 Source DF Type III SS Mean Square F Value Pr > F yr_rnd 1 99617.371 99617.371 21.00 <.0001 mealcat 2 3903569.804 1951784.902 411.46 <.0001 yr_rnd*mealcat 2 10583.519 5291.759 1.12 0.3288
We can also obtain parameter estimate by using the model option solution, which we will skip as we have seen before. It is easy to perform tests of simple main effects using the lsmeans statement shown below.
proc glm data="c:sasregelemapi2"; class yr_rnd mealcat; model api00=yr_rnd mealcat yr_rnd*mealcat /ss3; lsmeans yr_rnd*mealcat / slice=mealcat; run; quit;
The GLM Procedure
Least Squares Means
yr_rnd*mealcat Effect Sliced by mealcat for api00
Sum of
mealcat DF Squares Mean Square F Value Pr > F
1 1 36536 36536 7.70 0.0058
2 1 35593 35593 7.50 0.0064
3 1 38402 38402 8.10 0.0047
The results from above show us the effect of yr_rnd at each of the three levels of mealcat. We can see that the comparison for mealcat = 1 matches those we computed above using the test statement, however, it was much easier and less error prone using the lsmeans statement.
Although this section has focused on how to handle analyses involving interactions, these particular results show no indication of interaction. We could decide to omit interaction terms from future analyses having found the interactions to be non-significant. This would simplify future analyses, however including the interaction term can be useful to assure readers that the interaction term is non-significant.
3.6 Continuous and categorical variables
3.6.1 Using proc reg
Say that we wish to analyze both continuous and categorical variables in one analysis. For example, let’s include yr_rnd and some_col in the same analysis. We can also plot the predicted values against some_col using plot statement.
proc reg data="c:sasregelemapi2"; model api00 = yr_rnd some_col; run; quit;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 2 2072202 1036101 68.54 <.0001
Error 397 6001470 15117
Corrected Total 399 8073672
Root MSE 122.95143 R-Square 0.2567
Dependent Mean 647.62250 Adj R-Sq 0.2529
Coeff Var 18.98505
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 637.85807 13.50332 47.24 <.0001
yr_rnd year round school 1 -149.15906 14.87519 -10.03 <.0001
some_col parent some college 1 2.23569 0.55287 4.04 <.0001
proc reg data="c:sasregelemapi2";
model api00 = yr_rnd some_col;
output out=pred pred=p;
run;
quit;
symbol1 c=blue v=circle h=.8;
symbol2 c=red v=circle h=.8;
axis1 label=(r=0 a=90) minor=none;
axis2 minor=none;
proc gplot data=pred;
plot p*some_col=yr_rnd /vaxis=axis1 haxis=axis2;
run;
quit;
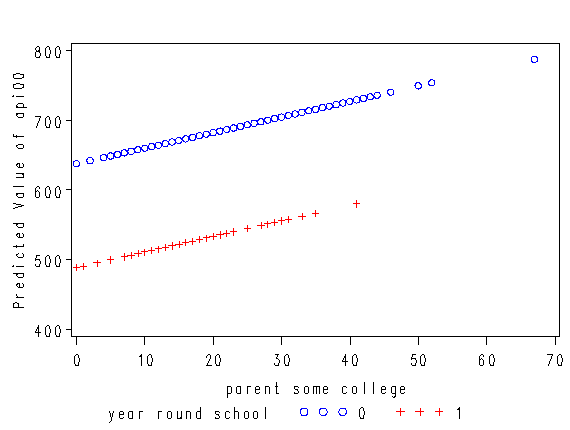
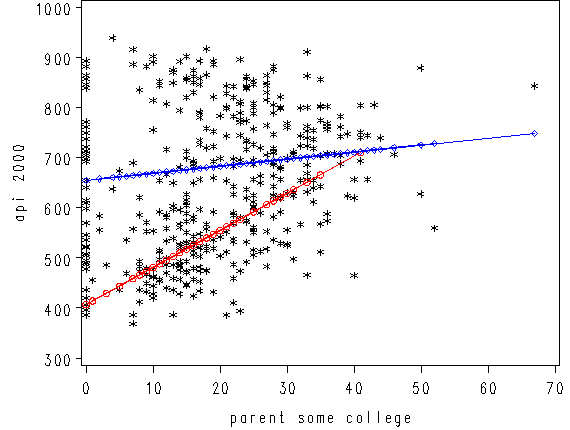
The coefficient for some_col indicates that for every unit increase in some_col the api00 score is predicted to increase by 2.23 units. This is the slope of the lines shown in the above graph. The graph has two lines, one for the year round schools and one for the non-year round schools. The coefficient for yr_rnd is -149.16, indicating that as yr_rnd increases by 1 unit, the api00 score is expected to decrease by about 149 units. As you can see in the graph, the top line is about 150 units higher than the lower line. You can see that the intercept is 637 and that is where the upper line crosses the Y axis when X is 0. The lower line crosses the line about 150 units lower at about 487.
3.6.2 Using proc glm
We can run this analysis using the proc glm for anova. The proc glm assumes that the independent variables are continuous. Thus, we need to use the class statement to specify which variables should be considered as categorical variables.
proc glm data="c:sasregelemapi2"; class yr_rnd; model api00=yr_rnd some_col /solution ss3; run; quit;
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 2 2072201.839 1036100.919 68.54 <.0001
Error 397 6001470.159 15117.053
Corrected Total 399 8073671.998
R-Square Coeff Var Root MSE api00 Mean
0.256662 18.98505 122.9514 647.6225
Source DF Type III SS Mean Square F Value Pr > F
yr_rnd 1 1519992.669 1519992.669 100.55 <.0001
some_col 1 247201.276 247201.276 16.35 <.0001
Standard
Parameter Estimate Error t Value Pr > |t|
Intercept 488.6990076 B 15.51331180 31.50 <.0001
yr_rnd 0 149.1590647 B 14.87518847 10.03 <.0001
yr_rnd 1 0.0000000 B . . .
some_col 2.2356887 0.55286556 4.04 <.0001
NOTE: The X'X matrix has been found to be singular, and a generalized inverse
was used to solve the normal equations. Terms whose estimates are
followed by the letter 'B' are not uniquely estimable.
If we square the t-values from the proc reg (above), we would find that they match those F-values of the proc glm. One thing you may notice that the parameter estimates above do not look quite the same as we did using proc reg. This is due to how proc glm processes a categorical (class) variable. We can get the same result if we code our class variable differently. This is shown below.
data temp; set "c:sasregelemapi2"; yrn=1-yr_rnd; run; proc glm data=temp; class yrn; model api00=yrn some_col /solution ss3; run; quit;
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 2 2072201.839 1036100.919 68.54 <.0001
Error 397 6001470.159 15117.053
Corrected Total 399 8073671.998
R-Square Coeff Var Root MSE api00 Mean
0.256662 18.98505 122.9514 647.6225
Source DF Type III SS Mean Square F Value Pr > F
yrn 1 1519992.669 1519992.669 100.55 <.0001
some_col 1 247201.276 247201.276 16.35 <.0001
Standard
Parameter Estimate Error t Value Pr > |t|
Intercept 637.8580723 B 13.50332419 47.24 <.0001
yrn 0 -149.1590647 B 14.87518847 -10.03 <.0001
yrn 1 0.0000000 B . . .
some_col 2.2356887 0.55286556 4.04 <.0001
NOTE: The X'X matrix has been found to be singular, and a generalized inverse
was used to solve the normal equations. Terms whose estimates are
followed by the letter 'B' are not uniquely estimable.
3.7 Interactions of Continuous by 0/1 Categorical variables
Above we showed an analysis that looked at the relationship between some_col and api00 and also included yr_rnd. We saw that this produced a graph where we saw the relationship between some_col and api00 but there were two regression lines, one higher than the other but with equal slope. Such a model assumed that the slope was the same for the two groups. Perhaps the slope might be different for these groups. Let’s run the regressions separately for these two groups beginning with the non-year round schools.
proc reg data="c:sasregelemapi2"; model api00 = some_col; where yr_rnd=0; run; quit;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 84701 84701 4.91 0.0274
Error 306 5273592 17234
Corrected Total 307 5358293
Root MSE 131.27818 R-Square 0.0158
Dependent Mean 684.53896 Adj R-Sq 0.0126
Coeff Var 19.17760
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 655.11030 15.23704 42.99 <.0001
some_col parent some college 1 1.40943 0.63576 2.22 0.0274
symbol1 i=none c=black v=circle h=0.5;
symbol2 i=join c=red v=dot h=0.5;
proc reg data="c:sasregelemapi2";
model api00 = some_col;
where yr_rnd=0;
plot (api00 predicted.)*some_col /overlay;
run;
quit;
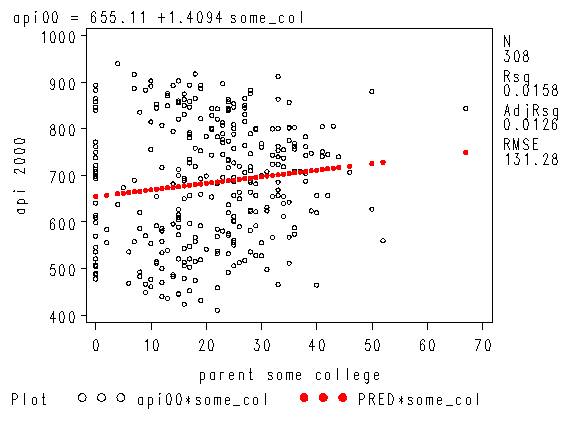
Likewise, let’s look at the year round schools and we will use the same symbol statements as above.
symbol1 i=none c=black v=circle h=0.5; symbol2 i=join c=red v=dot h=0.5; proc reg data="c:sasregelemapi2"; model api00 = some_col; where yr_rnd=1; plot (api00 predicted.)*some_col /overlay; run; quit;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 1 373644 373644 65.08 <.0001
Error 90 516735 5741.49820
Corrected Total 91 890379
Root MSE 75.77267 R-Square 0.4196
Dependent Mean 524.03261 Adj R-Sq 0.4132
Coeff Var 14.45953
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 407.03907 16.51462 24.65 <.0001
some_col parent some college 1 7.40262 0.91763 8.07 <.0001
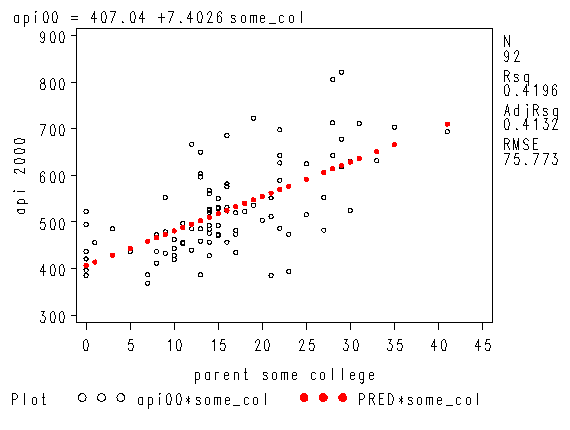
Note that the slope of the regression line looks much steeper for the year round schools than for the non-year round schools. This is confirmed by the regression equations that show the slope for the year round schools to be higher (7.4) than non-year round schools (1.3). We can compare these to see if these are significantly different from each other by including the interaction of some_col by yr_rnd, an interaction of a continuous variable by a categorical variable.
3.7.1 Computing interactions manually
We will start by manually computing the interaction of some_col by yr_rnd. Let’s start fresh and use the elemapi2 data file which should be sitting in your "c:sasreg" directory.
Next, let’s make a variable that is the interaction of some college (some_col) and year round schools (yr_rnd) called yrxsome.
data yrxsome_elemapi; set "c:sasregelemapi2"; yrxsome = yr_rnd*some_col; run;
We can now run the regression that tests whether the coefficient for some_col is significantly different for year round schools and non-year round schools. Indeed, the yrxsome interaction effect is significant.
proc reg data=yrxsome_elemapi; model api00 = some_col yr_rnd yrxsome; run; quit;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 3 2283345 761115 52.05 <.0001
Error 396 5790327 14622
Corrected Total 399 8073672
Root MSE 120.92161 R-Square 0.2828
Dependent Mean 647.62250 Adj R-Sq 0.2774
Coeff Var 18.67162
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 655.11030 14.03499 46.68 <.0001
some_col parent some college 1 1.40943 0.58560 2.41 0.0165
yr_rnd year round school 1 -248.07124 29.85895 -8.31 <.0001
yrxsome 1 5.99319 1.57715 3.80 0.0002
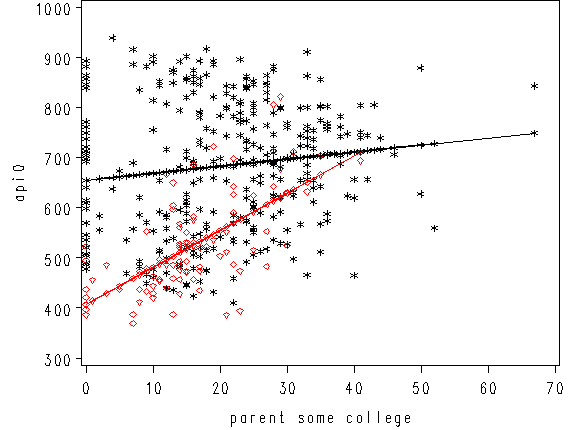
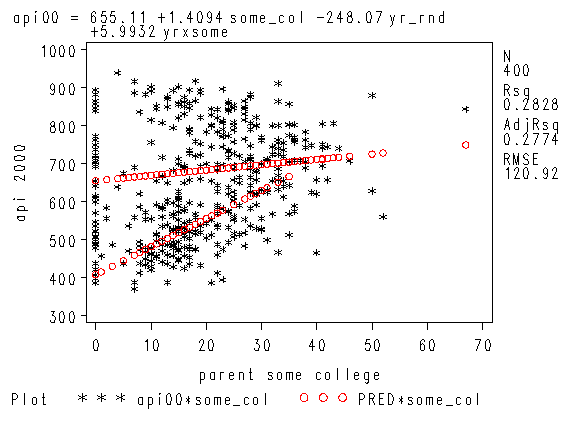
We can then save the predicted values to a data set and graph the predicted values for the two types of schools by some_col. You can see how the two lines have quite different slopes, consistent with the fact that the yrxsome interaction was significant.
proc reg data=yrxsome_elemapi; model api00 = some_col yr_rnd yrxsome; output out=temp pred=p; run; quit; axis1 label=(r=0 a=90) minor=none; axis2 minor = none; proc gplot data=temp; plot p*some_col=yr_rnd / haxis=axis2 vaxis=axis1; run; quit;
We can also create a plot including the data points. There are two ways of doing this and we’ll show both ways and their graphs here. One is to use the plot statement in proc reg.
symbol1 c=black v=star h=0.8; symbol2 c=red v=circle i=join h=0.8; proc reg data=yrxsome_elemapi; model api00 = some_col yr_rnd yrXsome; plot (api00 predicted.)*some_col/overlay; run; quit;
The other is to use proc gplot where we have more control over the look of the graph. In order to use proc gplot, we have to create a data set including the predicted value. This is done using the output statement in proc reg. In order to distinguish between the two groups of year-round schools and non-year-round schools we will do another data step where two variables of predicted values are created for each of the group.
proc reg data=yrxsome_elemapi; model api00 = some_col yr_rnd yrxsome; plot (api00 predicted.)*some_col/overlay; run; quit; data temp1; set temp; if yr_rnd=1 then p1=p; if yr_rnd=0 then p0=p; run; axis1 label=(r=0 a=90) minor=none; axis2 minor = none; symbol1 c=black v=star h=0.8; symbol2 c=red v=circle i=join h=0.8; symbol3 c=blue v=diamond i=join h=0.8; proc gplot data=temp1; plot (api00 p1 p0)*some_col / overlay haxis=axis2 vaxis=axis1; run; quit;
We can further enhance it so the data points are marked with different symbols. The graph above used the same kind of symbols for the data points for both types of schools. Let’s make separate variables for the api00 scores for the two types of schools called api0 for the non-year round schools and api1 for the year round schools.
data temp1; set temp; if yr_rnd=1 then do api1=api00; p1=p; end; if yr_rnd=0 then do api0=api00; p0=p; end; run;
We can then make the same graph as above except show the points differently for the two types of schools. Below we use stars for the non-year round schools, and diamonds for the year round schools.
goptions reset=all; axis1 label=(r=0 a=90) minor=none; axis2 minor = none; symbol1 c=black v=star h=0.8; symbol2 c=red v=diamond h=0.8; symbol3 c=black v=star i=join h=0.8; symbol4 c=red v=diamond i=join h=0.8; proc gplot data=temp1; plot api0*some_col=1 api1*some_col=2 p0*some_col=3 p1*some_col= 4 / overlay haxis=axis2 vaxis=axis1; run; quit;
Let’s quickly run the regressions again where we performed separate regressions for the two groups. We can first sort the data set by yr_rnd and make use of the by statement in the proc reg to perform separate regressions for the two groups. We also use the ODS (output delivery system) of SAS 8 to output the parameter estimate to a data set and print it out to compare the result.
proc sort data=yrxsome_elemapi;
by yr_rnd;
run;
ods listing close; /*stop output to appear in the output window*/
ods output ParameterEstimates=reg_some_col
(keep = yr_rnd Variable estimate );
proc reg data=yrxsome_elemapi;
by yr_rnd;
model api00=some_col;
run;
quit;
ods output close;
ods listing; /*put output back to the output window*/
proc print data=reg_some_col noobs;
run;
yr_rnd Variable Estimate 0 Intercept 655.11030 0 some_col 1.40943 1 Intercept 407.03907 1 some_col 7.40262
Now, let’s show the regression for both types of schools with the interaction term.
proc reg data=yrxsome_elemapi; model api00 = some_col yr_rnd yrxsome; output out=temp pred=p; run; quit;
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 655.11030 14.03499 46.68 <.0001
some_col parent some college 1 1.40943 0.58560 2.41 0.0165
yr_rnd year round school 1 -248.07124 29.85895 -8.31 <.0001
yrxsome 1 5.99319 1.57715 3.80 0.0002
Note that the coefficient for some_col in the combined analysis is the same as the coefficient for some_col for the non-year round schools? This is because non-year round schools are the reference group. Then, the coefficient for the yrxsome interaction in the combined analysis is the Bsome_col for the year round schools (7.4) minus Bsome_col for the non year round schools (1.41) yielding 5.99. This interaction is the difference in the slopes of some_col for the two types of schools, and this is why this is useful for testing whether the regression lines for the two types of schools are equal. If the two types of schools had the same regression coefficient for some_col, then the coefficient for the yrxsome interaction would be 0. In this case, the difference is significant, indicating that the regression lines are significantly different.
So, if we look at the graph of the two regression lines we can see the difference in the slopes of the regression lines (see graph below). Indeed, we can see that the non-year round schools (the solid line) have a smaller slope (1.4) than the slope for the year round schools (7.4). The difference between these slopes is 5.99, which is the coefficient for yrxsome.
3.7.2 Computing interactions with proc glm
We can also run a model just like the model we showed above using the proc glm. We can include the terms yr_rnd some_col and the interaction yr_rnr*some_col. Thus we can avoid a data step.
proc glm data="c:sasregelemapi2"; model api00 = yr_rnd some_col yr_rnd*some_col /ss3; run; quit;
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 3 2283345.485 761115.162 52.05 <.0001
Error 396 5790326.513 14622.037
Corrected Total 399 8073671.998
R-Square Coeff Var Root MSE api00 Mean
0.282814 18.67162 120.9216 647.6225
Source DF Type III SS Mean Square F Value Pr > F
yr_rnd 1 1009279.986 1009279.986 69.02 <.0001
some_col 1 84700.858 84700.858 5.79 0.0165
yr_rnd*some_col 1 211143.646 211143.646 14.44 0.0002
Standard
Parameter Estimate Error t Value Pr > |t|
Intercept 655.1103031 14.03499037 46.68 <.0001
yr_rnd -248.0712373 29.85894895 -8.31 <.0001
some_col 1.4094272 0.58560219 2.41 0.0165
yr_rnd*some_col 5.9931903 1.57714998 3.80 0.0002
In this section we found that the relationship between some_col and api00 depended on whether the school was from year round schools or from non-year round schools. For the schools from year round schools, the relationship between some_col and api00 was significantly stronger than for those from non-year round schools. In general, this type of analysis allows you to test whether the strength of the relationship between two continuous variables varies based on the categorical variable.
3.8 Continuous and categorical variables, interaction with 1/2/3 variable
The prior examples showed how to do regressions with a continuous variable and a categorical variable that has two levels. These examples will extend this further by using a categorical variable with three levels, mealcat.
3.8.1 Manually creating dummy variables
We can use a data step to create all the dummy variables needed for the interaction of mealcat and some_col just as we did before for mealcat. With the dummy variables, we can use proc reg for the regression analysis. We’ll use mealcat1 as the reference group.
data mxcol_elemapi;
set "c:sasregelemapi2";
array mealdum(3) mealcat1-mealcat3;
array mxcol(3) mxcol1-mxcol3;
do i = 1 to 3;
mealdum(i)=(mealcat=i);
mxcol(i)=mealdum(i)*some_col;
end;
drop i;
run;
proc reg data=mxcol_elemapi;
model api00 = some_col mealcat2 mealcat3 mxcol2 mxcol3;
run;
quit;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 5 6212307 1242461 263.00 <.0001
Error 394 1861365 4724.27696
Corrected Total 399 8073672
Root MSE 68.73338 R-Square 0.7695
Dependent Mean 647.62250 Adj R-Sq 0.7665
Coeff Var 10.61319
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 825.89370 11.99182 68.87 <.0001
some_col parent some college 1 -0.94734 0.48737 -1.94 0.0526
mealcat2 1 -239.02998 18.66502 -12.81 <.0001
mealcat3 1 -344.94758 17.05743 -20.22 <.0001
mxcol2 1 3.14094 0.72929 4.31 <.0001
mxcol3 1 2.60731 0.89604 2.91 0.0038
The interaction now has two terms (mxcol2 and mxcol3). To get an overall test of this interaction, we can use the test command.
proc reg data=mxcol_elemapi; model api00 = some_col mealcat2 mealcat3 mxcol2 mxcol3; test mxcol2=mxcol3=0; run; quit;
Test 1 Results for Dependent Variable api00
Mean
Source DF Square F Value Pr > F
Numerator 2 48734 10.32 <.0001
Denominator 394 4724.27696
These results indicate that the overall interaction is indeed significant. This means that the regression lines from the three groups differ significantly. As we have done before, let’s compute the predicted values and make a graph of the predicted values so we can see how the regression lines differ.
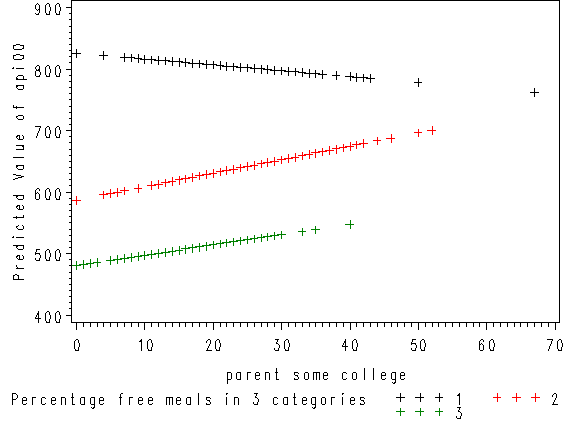
proc reg data=mxcol_elemapi; model api00 = some_col mealcat2 mealcat3 mxcol2 mxcol3; output out=pred predicted=p; run; quit; goptions reset=all; axis1 label=(r=0 a=90); proc gplot data=pred; plot p*some_col=mealcat /vaxis=axis1; run; quit;
Since we had three groups, we get three regression lines, one for each category of mealcat. The solid line is for group 1, the dashed line for group 2, and the dotted line is for group 3.
Group 1 was the omitted group, therefore the slope of the line for group 1 is the coefficient for some_col which is -.94. Indeed, this line has a downward slope. If we add the coefficient for some_col to the coefficient for mxcol2 we get the coefficient for group 2, i.e., 3.14 + (-.94) yields 2.2, the slope for group 2. Indeed, group 2 shows an upward slope. Likewise, if we add the coefficient for some_col to the coefficient for mxcol3 we get the coefficient for group 3, i.e., 2.6 + (-.94) yields 1.66, the slope for group 3,. So, the slopes for the 3 groups are
group 1: -0.94 group 2: 2.2 group 3: 1.66
The test of the coefficient in the parameter estimates for mxcol2 tested whether the coefficient for group 2 differed from group 1, and indeed this was significant. Likewise, the test of the coefficient for mxcol3 tested whether the coefficient for group 3 differed from group 1, and indeed this was significant. What did the test of the coefficient some_col test? This coefficient represents the coefficient for group 1, so this tested whether the coefficient for group 1 (-0.94) was significantly different from 0. This is probably a non-interesting test.
The comparisons in the above analyses don’t seem to be as interesting as comparing group 1 versus 2 and then comparing group 2 versus 3. These successive comparisons seem much more interesting. We can do this by making group 2 the omitted group, and then each group would be compared to group 2.
proc reg data=mxcol_elemapi; model api00 = some_col mealcat1 mealcat3 mxcol1 mxcol3; run; quit;
Analysis of Variance
Sum of Mean
Source DF Squares Square F Value Pr > F
Model 5 6212307 1242461 263.00 <.0001
Error 394 1861365 4724.27696
Corrected Total 399 8073672
Root MSE 68.73338 R-Square 0.7695
Dependent Mean 647.62250 Adj R-Sq 0.7665
Coeff Var 10.61319
Parameter Estimates
Parameter Standard
Variable Label DF Estimate Error t Value Pr > |t|
Intercept Intercept 1 586.86372 14.30311 41.03 <.0001
some_col parent some college 1 2.19361 0.54253 4.04 <.0001
mealcat1 1 239.02998 18.66502 12.81 <.0001
mealcat3 1 -105.91760 18.75450 -5.65 <.0001
mxcol1 1 -3.14094 0.72929 -4.31 <.0001
mxcol3 1 -0.53364 0.92720 -0.58 0.5653
Now, the test of mxcol1 tests whether the coefficient for group 1 differs from group 2, and it does. Then, the test of mxcol3 tests whether the coefficient for group 3 significantly differs from group 2, and it does not. This makes sense given the graph and given the estimates of the coefficients that we have, that -.94 is significantly different from 2.2 but 2.2 is not significantly different from 1.66.
3.8.2 Using proc glm
We can perform the same analysis using the proc glm command, as shown below. The proc glm allows us to avoid dummy coding for either the categorical variable mealcat and for the interaction term of mealcat and some_col. The tricky part is to control the reference group.
proc glm data="c:sasregelemapi2"; class mealcat; model api00=some_col mealcat some_col*mealcat /solution ss3; run; quit;
Sum of
Source DF Squares Mean Square F Value Pr > F
Model 5 6212306.876 1242461.375 263.00 <.0001
Error 394 1861365.121 4724.277
Corrected Total 399 8073671.998
R-Square Coeff Var Root MSE api00 Mean
0.769452 10.61319 68.73338 647.6225
Source DF Type III SS Mean Square F Value Pr > F
some_col 1 36366.366 36366.366 7.70 0.0058
mealcat 2 2012065.492 1006032.746 212.95 <.0001
some_col*mealcat 2 97468.169 48734.084 10.32 <.0001
Standard
Parameter Estimate Error t Value Pr > |t|
Intercept 480.9461176 B 12.13062708 39.65 <.0001
some_col 1.6599700 B 0.75190859 2.21 0.0278
mealcat 1 344.9475807 B 17.05743173 20.22 <.0001
mealcat 2 105.9176024 B 18.75449819 5.65 <.0001
mealcat 3 0.0000000 B . . .
some_col*mealcat 1 -2.6073085 B 0.89604354 -2.91 0.0038
some_col*mealcat 2 0.5336362 B 0.92720142 0.58 0.5653
some_col*mealcat 3 0.0000000 B . . .
NOTE: The X'X matrix has been found to be singular, and a generalized inverse
was used to solve the normal equations. Terms whose estimates are
followed by the letter 'B' are not uniquely estimable.
Because the default order for categorical variables is their numeric values, glm omits the third category. On the other hand, the analysis we showed in previous section omitted the second category, the parameter estimates will not be the same. You can compare the results from below with the results above and see that the parameter estimates are not the same. Because group 3 is dropped, that is the reference category and all comparisons are made with group 3. Other than default order, proc glm also allows freq count order, which in our case is the same as the default order since group 3 has the most count.
These analyses showed that the relationship between some_col and api00 varied, depending on the level of mealcat. In comparing group 1 with group 2, the coefficient for some_col was significantly different, but there was no difference in the coefficient for some_col in comparing groups 2 and 3.
3.9 Summary
This chapter covered some techniques for analyzing data with categorical variables, especially, manually constructing indicator variables and using the proc glm. Each method has its advantages and disadvantages, as described below.
Manually constructing indicator variables can be very tedious and even error prone. For very simple models, it is not very difficult to create your own indicator variables, but if you have categorical variables with many levels and/or interactions of categorical variables, it can be laborious to manually create indicator variables. However, the advantage is that you can have quite a bit of control over how the variables are created and the terms that are entered into the model.
The proc glm approach eliminates the need to create indicator variables making it easy to include variables that have lots of categories, and making it easy to create interactions by allowing you to include terms like some_col*mealcat. It can be easier to perform tests of simple main effects with the proc glm. However, the proc glm is not very flexible in letting you choose which category is the omitted category.
As you will see in the next chapter, the regress command includes additional options like the robust option and the cluster option that allow you to perform analyses when you don’t exactly meet the assumptions of ordinary least squares regression. In such cases, the regress command offers features not available in the anova command and may be more advantageous to use.
3.10 For more information
- SAS/Stat Manual
- Proc Reg and Proc GLM
- Web Links
- Creating Dummy Variables
- Models with interactions of continuous and categorical variables