Introduction
Power analysis is the name given to the process for determining the sample size for a research study. The technical definition of power is that it is the probability of detecting a “true” effect when it exists. Many students think that there is a simple formula for determining sample size for every research situation. However, the reality it that there are many research situations that are so complex that they almost defy rational power analysis. In most cases, power analysis involves a number of simplifying assumptions, in order to make the problem tractable, and running the analyses numerous times with different variations to cover all of the contingencies.
In this unit we will try to illustrate the power analysis process using a simple four group design.
Description of the Experiment
We wish to conduct a study in the area of mathematics education involving different teaching methods to improve standardized math scores in local classrooms. The study will include four different teaching methods and use fourth grade students who are randomly sampled from a large urban school district and are then random assigned to the four different teaching methods.
Here are the four different teaching methods which will be examined: 1) The traditional teaching method where the classroom teacher explains the concepts and assigns homework problems from the textbook; 2) the intensive practice method, in which students fill out additional work sheets both before and after school; 3) the computer assisted method, in which students learn math concepts and skills from using various computer based math learning programs; and, 4) the peer assistance learning method, which pairs each fourth grader with a fifth grader who helps them learn the concepts followed by the student teaching the same material to another student in their group.
Students will stay in their math learning groups for an entire academic year. At the end of the Spring semester all students will take the Multiple Math Proficiency Inventory (MMPI). This standardized test has a mean for fourth graders of 550 with a standard deviation of 80.
The experiment is designed so that each of the four groups will have the same sample size. One of the important questions we need to answer in designing the study is, how many students will be needed in each group?
The Power Analysis
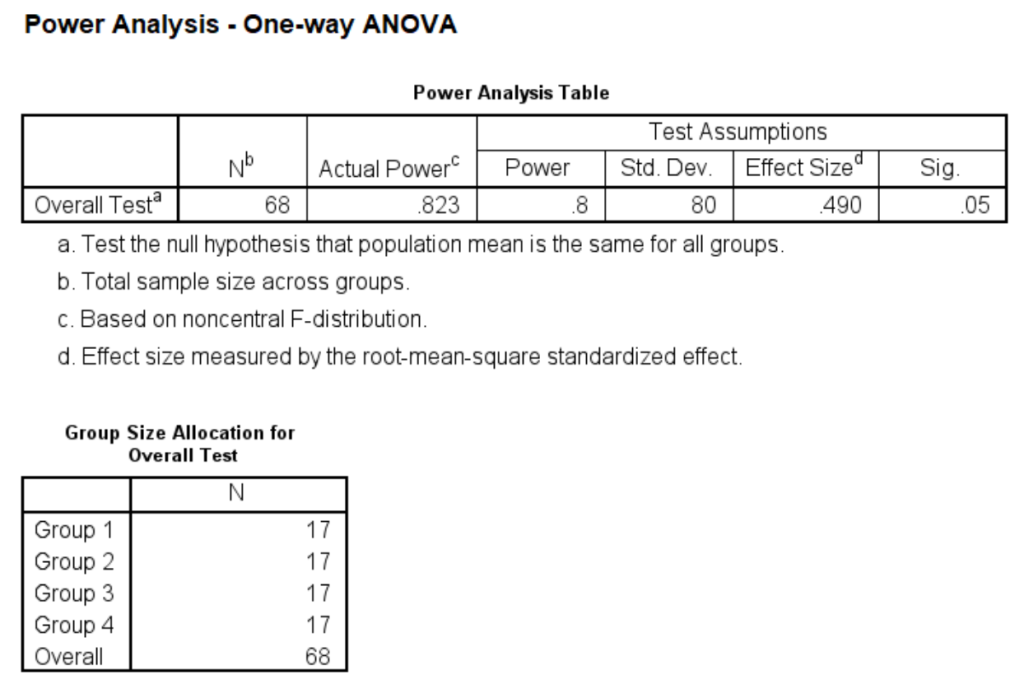
In order to answer this question, we will need to make some assumptions and some educated guesses about the data. First, we will assume that the standard deviation for each of the four groups will be equal and will be equal to the national value of 80. Further, we expect, because of prior research, that the traditional teaching group (Group 1) will have the lowest mean score and that the peer assistance group (Group 4) will have the highest mean score on the MMPI. In fact, we expect that Group 1 will have a mean of 550 and that Group 4 will have mean that is greater by 1.2 standard deviations, i.e., the mean will equal at least 646. For the sake of simplicity, we will assume that the means of the other two groups will be equal to the grand mean.
We will make use of SPSS’s command power oneway anova to do the power analysis. As stated above, there are four groups, a=4. We will set alpha = 0.05, and we will compute the effect size, delta = (largest_mean – smallest_mean)/standard_deviation. Hence, delta = (646-550)/80 = 1.2 . The standard deviation we use is the pooled within-group standard deviation, i.e., the square root of the mean square error for the ANOVA table.
power oneway anova
/parameters power=.8 pooled_sd=80 group_weights=1 1 1 1 group_means=550 598 598 646
significance=0.05.
The table above shows that we can achieve a power of 0.823 with 17 students per group.
While 17 students per group sound like a fine number of subjects if everything works out as planned, we should consider what would occur if things do not work out as planned. Let’s say that the treatment effect is not a large 1.2 but a more modest .75.
power oneway anova
/parameters power=.8 pooled_sd=80 group_weights=1 1 1 1 group_means=550 580 580 610
significance=0.05.
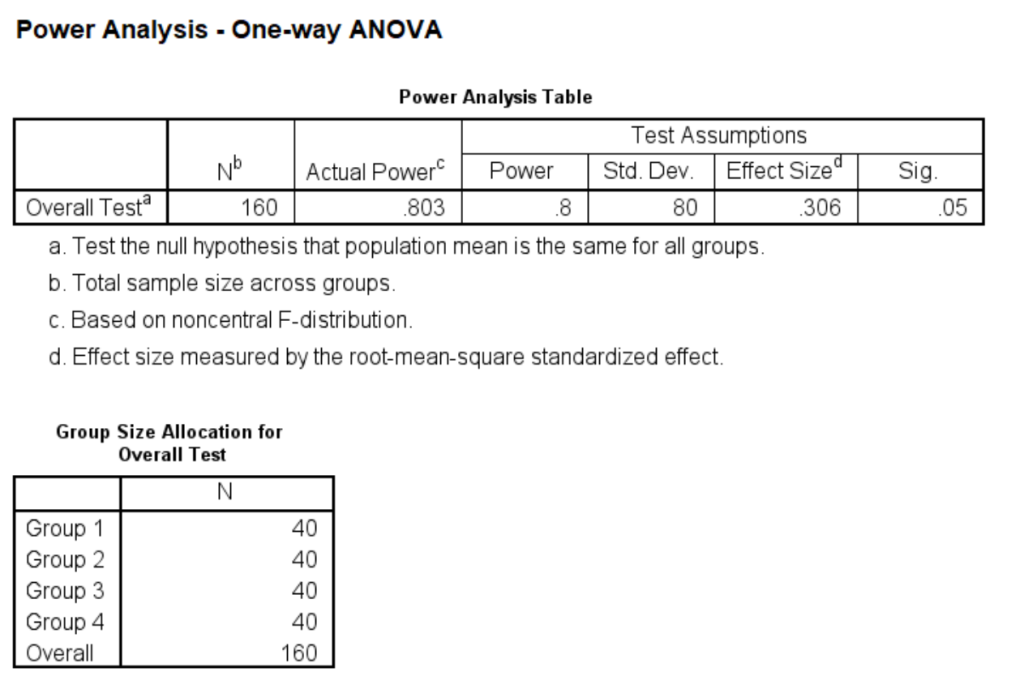
Forty students per group gives us a power just above 0.8.
The effect size of 0.75 is considered moderate. Finally, just to be safe, we should see what sample size would be needed if the there was a small effect size of, say, 0.25.
power oneway anova
/parameters power=.8 pooled_sd=80 group_weights=1 1 1 1 group_means=550 560 560 570
significance=0.05.
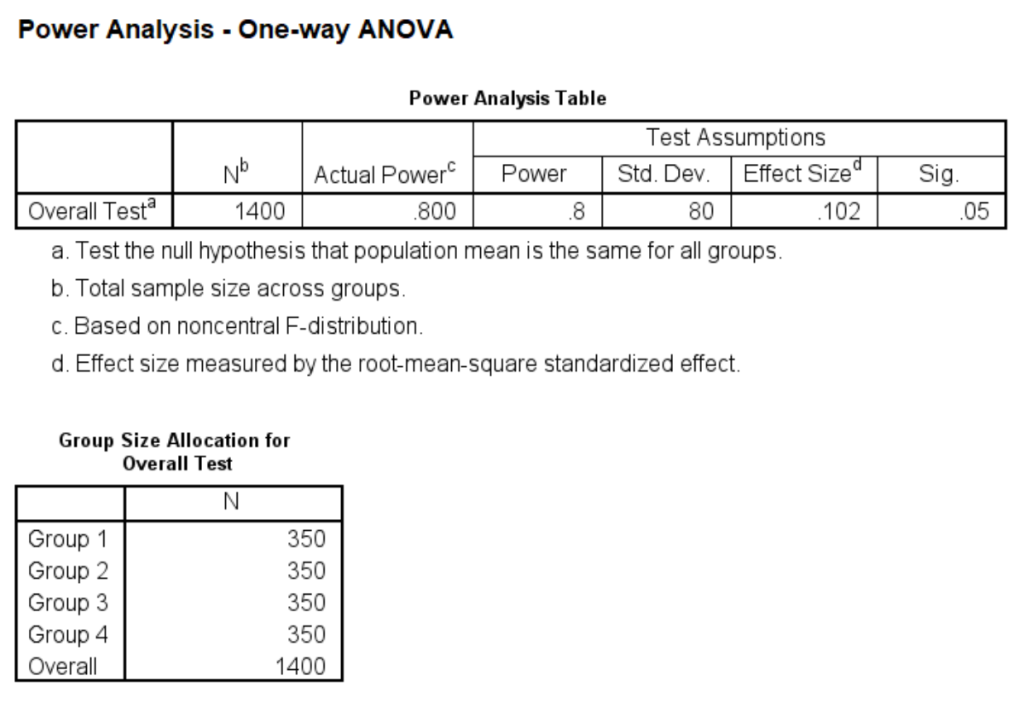
An N of about 350 per group is needed to obtain a power of 0.8 when the effect size is 0.25.
Here are the sample sizes per group that we have come up with in our power analysis: 17 (best case scenario), 40 (medium effect size), and 350 (almost the worst case scenario). Even though we expect a large effect, we will shoot for a sample size of approximately 40 students per group. For one thing, it is all that our research budget will allow and the school district won’t allow us to use more than 200 students total.
References
Cohen, J. 1988. Statistical Power Analysis for the Behavioral Sciences, Second Edition. Mahwah, NJ: Lawrence Erlbaum Associates.