Version info: Code for this page was tested in IBM SPSS 20.
MANOVA is used to model two or more dependent variables that are continuous with one or more categorical predictor variables.
Please note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and checking, verification of assumptions, model diagnostics or potential follow-up analyses.
Examples of one-way multivariate analysis of variance
Example 1.
A researcher randomly assigns 33 subjects to one of three groups. The first group receives technical dietary information interactively from an on-line website. Group 2 receives the same information from a nurse practitioner, while group 3 receives the information from a video tape made by the same nurse practitioner. The researcher looks at three different ratings of the presentation, difficulty, usefulness and importance, to determine if there is a difference in the modes of presentation. In particular, the researcher is interested in whether the interactive website is superior because that is the most cost-effective way of delivering the information.
Example 2. A clinical psychologist recruits 100 people who suffer from panic disorder into his study. Each subject receives one of four types of treatment for eight weeks. At the end of treatment, each subject participates in a structured interview, during which the clinical psychologist makes three ratings: physiological, emotional and cognitive. The clinical psychologist wants to know which type of treatment most reduces the symptoms of the panic disorder as measured on the physiological, emotional and cognitive scales. (This example was adapted from Grimm and Yarnold, 1995, page 246.)
Description of the data
Let’s pursue Example 1 from above.
We have a data file, manova.sav, with 33 observations on three response variables. The response variables are ratings called useful, difficulty and importance. Level 1 of the group variable is the treatment group, level 2 is control group 1 and level 3 is control group 2.
Let’s look at the data. It is always a good idea to start with descriptive statistics.
get file='d:\data\manova.sav' . descriptives variables=difficulty useful importance.
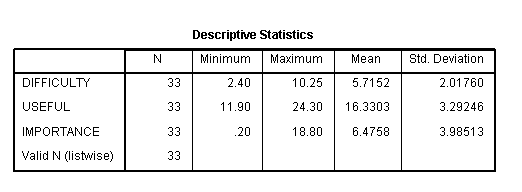
frequencies variables=group.
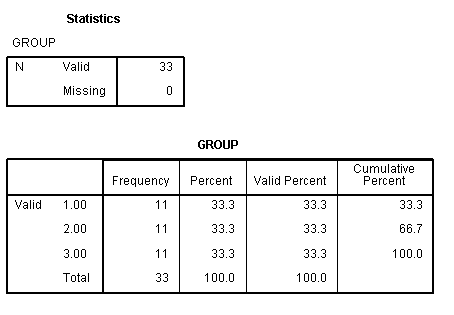
means tables=difficulty useful importance by group.
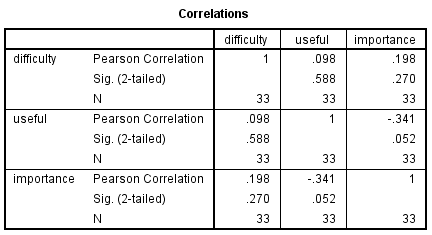
correlations variables=difficulty useful importance.
Analysis methods you might consider
Below is a list of some analysis methods you may have encountered. Some of the methods listed are quite reasonable, while others have either fallen out of favor or have limitations.
- MANOVA – This is a good option if there are two or more continuous dependent variables and one categorical predictor variable.
- Discriminant function analysis – This is a reasonable option and is equivalent to a one-way MANOVA.
- The data could be reshaped into long format and analyzed as a multilevel model.
- Separate univariate ANOVAs – You could analyze these data using separate univariate ANOVAs for each response variable. The univariate ANOVA will not produce multivariate results utilizing information from all variables simultaneously. In addition, separate univariate tests are generally less powerful because they do not take into account the inter-correlation of the dependent variables.
One-way MANOVA
We will start by running the manova command. After the categorical predictor variable group, we need to specify the minimum and maximum values of that variable in parentheses.
manova difficulty useful importance by group(1,3).
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
The default error term in MANOVA has been changed from WITHIN CELLS to
WITHIN+RESIDUAL. Note that these are the same for all full factorial designs.
* * * * * * * * * * * * * * * * * A n a l y s i s o f V a r i a n c e * * * * * * * * * * * * * * * * *
33 cases accepted.
0 cases rejected because of out-of-range factor values.
0 cases rejected because of missing data.
3 non-empty cells.
1 design will be processed.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
* * * * * * * * * * * * * * * * * A n a l y s i s o f V a r i a n c e -- Design 1 * * * * * * * * * * * * * * * * *
EFFECT .. GROUP
Multivariate Tests of Significance (S = 2, M = 0, N = 13 )
Test Name Value Approx. F Hypoth. DF Error DF Sig. of F
Pillais .47667 3.02483 6.00 58.00 .012
Hotellings .89723 4.03753 6.00 54.00 .002
Wilks .52579 3.53823 6.00 56.00 .005
Roys .47146
Note.. F statistic for WILKS' Lambda is exact.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
EFFECT .. GROUP (Cont.)
Univariate F-tests with (2,30) D. F.
Variable Hypoth. SS Error SS Hypoth. MS Error MS F Sig. of F
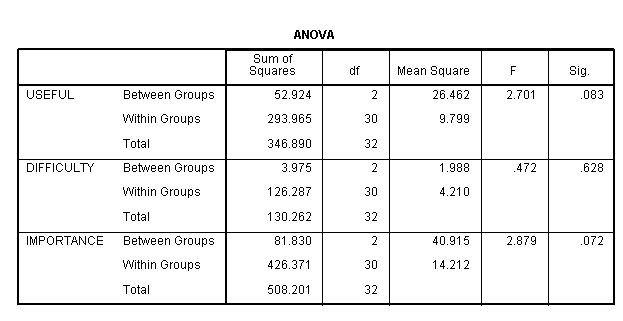
DIFFICUL 3.97515 126.28728 1.98758 4.20958 .47216 .628
USEFUL 52.92424 293.96544 26.46212 9.79885 2.70053 .083
IMPORTAN 81.82969 426.37090 40.91485 14.21236 2.87882 .072
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Abbreviated Extended
Name Name
DIFFICUL DIFFICULTY
IMPORTAN IMPORTANCE
- At the top of the output, we can see that all 33 cases in our dataset are used in the analysis.
- Next we see a table of the multivariate tests. All of the tests of the overall model are statistically significant. For more information on the various multivariate tests, please see our Annotated Output: SPSS MANOVA.
- In the third part of the output, we see the tests of the individual outcome variables. Individually, none of the outcome variables is statistically significant at the .05 level of alpha.
- Finally, we see legend showing us how SPSS abbreviated the names of some of the outcome variables.
We will begin by comparing the treatment group (group 1) to an average of the control groups (groups 2 and 3). This tests the hypothesis that the mean of the control groups equals the treatment group. We will also compare control group 1 (group 2) to control group 2 (group 3). The first hypothesis is given on the second line of the contrast subcommand, and the second hypothesis is given on the third line of the contrast subcommand.
manova difficulty useful importance by group(1,3) /contrast(group) = special (1 1 1 2 -1 -1 0 1 -1) /design = group(1) group(2).< some output omitted > * * * * * * * * * * * * * * * * * A n a l y s i s o f V a r i a n c e -- Design 1 * * * * * * * * * * * * * * * * * EFFECT .. GROUP(1) Multivariate Tests of Significance (S = 1, M = 1/2, N = 13 ) Test Name Value Exact F Hypoth. DF Error DF Sig. of F Pillais .47101 8.31034 3.00 28.00 .000 Hotellings .89039 8.31034 3.00 28.00 .000 Wilks .52899 8.31034 3.00 28.00 .000 Roys .47101 Note.. F statistics are exact. - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - EFFECT .. GROUP(1) (Cont.) Univariate F-tests with (1,30) D. F. Variable Hypoth. SS Error SS Hypoth. MS Error MS F Sig. of F DIFFICUL 3.73470 126.28728 3.73470 4.20958 .88719 .354 USEFUL 52.74242 293.96544 52.74242 9.79885 5.38251 .027 IMPORTAN 80.30060 426.37090 80.30060 14.21236 5.65005 .024 < some output omitted >
- These results indicate that group 1 is statistically significantly different from the average of groups 2 and 3.
< some output omitted >* * * * * * * * * * * * * * * * * A n a l y s i s o f V a r i a n c e -- Design 1 * * * * * * * * * * * * * * * * * EFFECT .. GROUP(2) Multivariate Tests of Significance (S = 1, M = 1/2, N = 13 ) Test Name Value Exact F Hypoth. DF Error DF Sig. of F Pillais .00679 .06381 3.00 28.00 .979 Hotellings .00684 .06381 3.00 28.00 .979 Wilks .99321 .06381 3.00 28.00 .979 Roys .00679 Note.. F statistics are exact. - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - EFFECT .. GROUP(2) (Cont.) Univariate F-tests with (1,30) D. F. Variable Hypoth. SS Error SS Hypoth. MS Error MS F Sig. of F DIFFICUL .24045 126.28728 .24045 4.20958 .05712 .813 USEFUL .18182 293.96544 .18182 9.79885 .01856 .893 IMPORTAN 1.52909 426.37090 1.52909 14.21236 .10759 .745 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -< some output omitted >
- The results indicate that control group 1 is not statistically significantly different from control group 2.
We can use the pmeans subcommand to obtain adjusted predicted values for each of the groups. In the first table below, we get the predicted means for the dependent variable difficulty. In the next two tables, we get the predicted means for the dependent variables useful and importance. These values can be helpful in seeing where differences between levels of the predictor variable are and describing the model.
manova difficulty useful importance by group(1,3) /pmeans.< some output omitted >- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Adjusted and Estimated Means Variable .. DIFFICULTY Factor Code Obs. Mean Adj. Mean Est. Mean Raw Resid. Std. Resid. GROUP 1 6.19091 6.19091 6.19091 .00000 .00000 GROUP 2 5.58182 5.58182 5.58182 .00000 .00000 GROUP 3 5.37273 5.37273 5.37273 .00000 .00000 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Adjusted and Estimated Means (Cont.) Variable .. USEFUL Factor Code Obs. Mean Adj. Mean Est. Mean Raw Resid. Std. Resid. GROUP 1 18.11818 18.11818 18.11818 .00000 .00000 GROUP 2 15.52727 15.52727 15.52727 .00000 .00000 GROUP 3 15.34545 15.34545 15.34545 .00000 .00000 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Adjusted and Estimated Means (Cont.) Variable .. IMPORTANCE Factor Code Obs. Mean Adj. Mean Est. Mean Raw Resid. Std. Resid. GROUP 1 8.68182 8.68182 8.68182 .00000 .00000 GROUP 2 5.10909 5.10909 5.10909 .00000 .00000 GROUP 3 5.63636 5.63636 5.63636 .00000 .00000 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -< some output omitted >
In each of the three tables above, we see that the predicted means for groups 2 and 3 are very similar; the predicted mean for group 1 is higher than those for groups 2 and 3.
In the example below, we obtain the differences in the means for each of the dependent variables for each of the control groups (groups 2 and 3) compared to the treatment group (group 1). With respect to the dependent variable difficulty, the difference between the means for control group 1 versus the treatment group is approximately -0.61 (5.58 – 6.19). The difference between the means for control group 2 versus the treatment group is approximately -0.82 (5.37 – 6.19).
manova difficulty useful importance by group(1,3) /contrast(group) = special(1 1 1 -1 1 0 -1 0 1).< some output omitted >- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Estimates for DIFFICULTY --- Individual univariate .9500 confidence intervals GROUP Parameter Coeff. Std. Err. t-Value Sig. t Lower -95% CL- Upper 2 -.6090908051 .87486 -.69622 .49165 -2.39579 1.17761 3 -.8181818182 .87486 -.93522 .35714 -2.60488 .96852 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Estimates for USEFUL --- Individual univariate .9500 confidence intervals GROUP Parameter Coeff. Std. Err. t-Value Sig. t Lower -95% CL- Upper 2 -2.5909088308 1.33477 -1.94109 .06169 -5.31687 .13505 3 -2.7727272727 1.33477 -2.07731 .04643 -5.49869 -.04676 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Estimates for IMPORTANCE --- Individual univariate .9500 confidence intervals GROUP Parameter Coeff. Std. Err. t-Value Sig. t Lower -95% CL- Upper 2 -3.5727272291 1.60750 -2.22253 .03393 -6.85569 -.28977 3 -3.0454544317 1.60750 -1.89452 .06783 -6.32841 .23750 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -< some output omitted >
Finally, let’s run separate univariate ANOVAs.
oneway useful difficulty importance by group.
While none of the three ANOVAs were statistically significant at the alpha = .05 level, in particular, the F-ratio for difficulty was less than 1.
Things to consider
- One of the assumptions of MANOVA is that the response variables come from group populations that are multivariate normal distributed. This means that each of the dependent variables is normally distributed within group, that any linear combination of the dependent variables is normally distributed, and that all subsets of the variables must be multivariate normal. With respect to Type I error rate, MANOVA tends to be robust to minor violations of the multivariate normality assumption.
- The homogeneity of population covariance matrices (a.k.a. sphericity) is another assumption. This implies that the population variances and covariances of all dependent variables must be equal in all groups formed by the independent variables.
- Small samples can have low power, but if the multivariate normality assumption is met, the MANOVA is generally more powerful than separate univariate tests.
- There are at least five types of follow-up analyses that can be done after a statistically significant MANOVA. These include multiple univariate ANOVAs, stepdown analysis, discriminant analysis, dependent variable contribution, and multivariate contrasts.
See also
References
- Grimm, L. G. and Yarnold, P. R. (editors). 1995. Reading and Understanding Multivariate Statistics. Washington, D.C.: American Psychological Association.
- Huberty, C. J. and Olejnik, S. 2006. Applied MANOVA and Discriminant Analysis, Second Edition. Hoboken, New Jersey: John Wiley and Sons, Inc.
- Stevens, J. P. 2002. Applied Multivariate Statistics for the Social Sciences, Fourth Edition. Mahwah, New Jersey: Lawrence Erlbaum Associates, Inc.
- Tatsuoka, M. M. 1971. Multivariate Analysis: Techniques for Educational and Psychological Research. New York: John Wiley and Sons.