Table 2.3, page 25: A data set with a perfect nonlinear relationship between Y and X, yet Cor(X,Y) = 0
get file 'D:p025a.sav'. list.
y x
1 -7
14 -6
25 -5
34 -4
41 -3
46 -2
49 -1
50 0
49 1
46 2
41 3
34 4
25 5
14 6
1 7
Number of cases read: 15 Number of cases listed: 15
Figure 2.2, page 25: A scatter plot of Y versus X in Table 2.3
graph /scatter = x with y.
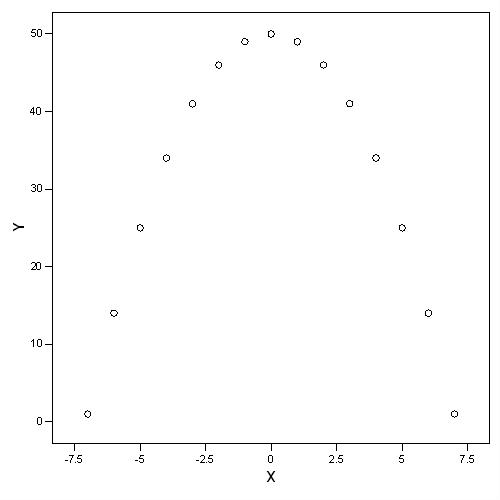
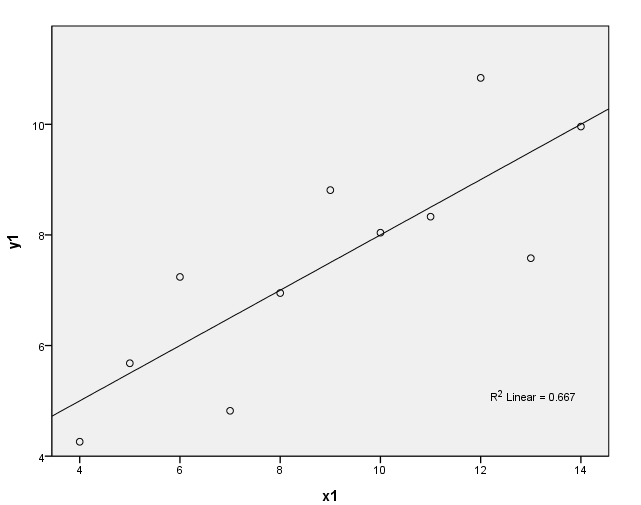
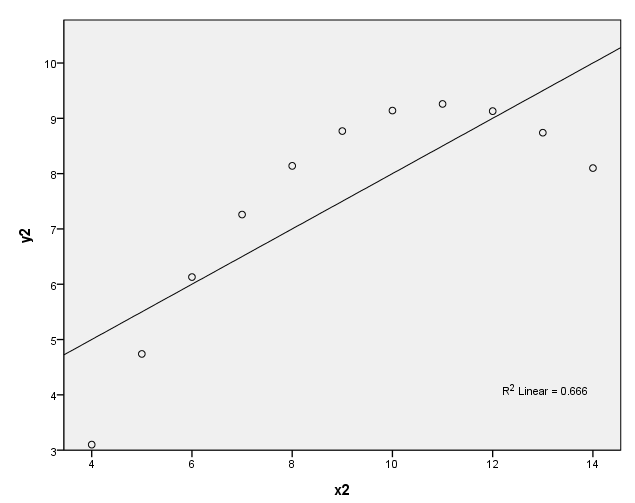
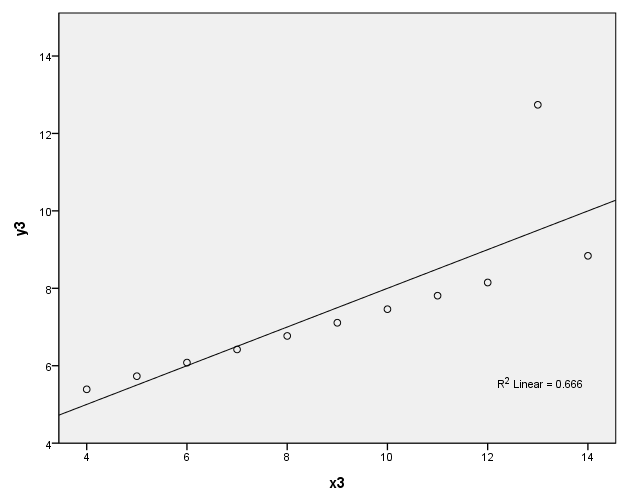
Table 2.4, page 25 Anscombe’s Quartet: Four data sets having same values of summary statistics
get file 'D:p025b.sav'.
list.
y1 x1 y2 x2 y3 x3 y4 x4
8.04 10 9.14 10 7.46 10 6.58 8
6.95 8 8.14 8 6.77 8 5.76 8
7.58 13 8.74 13 12.74 13 7.71 8
8.81 9 8.77 9 7.11 9 8.84 8
8.33 11 9.26 11 7.81 11 8.47 8
9.96 14 8.10 14 8.84 14 7.04 8
7.24 6 6.13 6 6.08 6 5.25 8
4.26 4 3.10 4 5.39 4 12.50 19
10.84 12 9.13 12 8.15 12 5.56 8
4.82 7 7.26 7 6.42 7 7.91 8
5.68 5 4.74 5 5.73 5 6.89 8
Number of cases read: 11 Number of cases listed: 11
Figure 2.3, page 26: Scatter plots of the data in Table 2.4 with the fitted lines
graph (a)
formats y1 x1 y2 x2 y3 x3 y4 x4 (f2.0).
GGRAPH
/GRAPHDATASET NAME="GraphDataset" VARIABLES= y1 x1
/GRAPHSPEC SOURCE=INLINE
INLINETEMPLATE=["<addFitLine type='linear' target='pair'/> " ].
BEGIN GPL
SOURCE: s=userSource( id( "GraphDataset" ) )
DATA: y1=col( source(s), name( "y1" ) )
DATA: x1=col( source(s), name( "x1" ) )
GUIDE: axis( dim( 1 ), label( "x1" ) )
GUIDE: axis( dim( 2 ), label( "y1" ) )
ELEMENT: point( position( ( X1_Var * Y_Var ) ) )
END GPL.
graph (b)
GGRAPH /GRAPHDATASET NAME="GraphDataset" VARIABLES= y2 x2 /GRAPHSPEC SOURCE=INLINE INLINETEMPLATE=["<addFitLine type='linear' target='pair'/> "]. BEGIN GPL SOURCE: s=userSource( id( "GraphDataset" ) ) DATA: y2=col( source(s), name( "y2" ) ) DATA: x2=col( source(s), name( "x2" ) ) GUIDE: axis( dim( 1 ), label( "x2" ) ) GUIDE: axis( dim( 2 ), label( "y2" ) ) ELEMENT: point( position( (x2 * y2 ) ) ) END GPL.
graph (c)
GGRAPH /GRAPHDATASET NAME="GraphDataset" VARIABLES= y3 x3 /GRAPHSPEC SOURCE=INLINE INLINETEMPLATE=["<addFitLine type='linear' target='pair'/> " ]. BEGIN GPL SOURCE: s=userSource( id( "GraphDataset" ) ) DATA: y3=col( source(s), name( "y3" ) ) DATA: x3=col( source(s), name( "x3" ) ) GUIDE: axis( dim( 1 ), label( "x3" ) ) GUIDE: axis( dim( 2 ), label( "y3" ) ) ELEMENT: point( position( ( x3 * y3 ) ) ) END GPL.
graph (d)
GGRAPH
/GRAPHDATASET NAME="GraphDataset" VARIABLES= y4 x4
/GRAPHSPEC SOURCE=INLINE INLINETEMPLATE=["<addFitLine type='linear' target='pair'/> "].
BEGIN GPL
SOURCE: s=userSource( id( "GraphDataset" ) )
DATA: y4=col( source(s), name( "y4" ) )
DATA: x4=col( source(s), name("x4") )
GUIDE: axis( dim( 1 ), label( "x4" ) )
GUIDE: axis( dim( 2 ), label( "y4" ) )
ELEMENT: point( position( ( x4 * y4 ) ) )
END GPL.
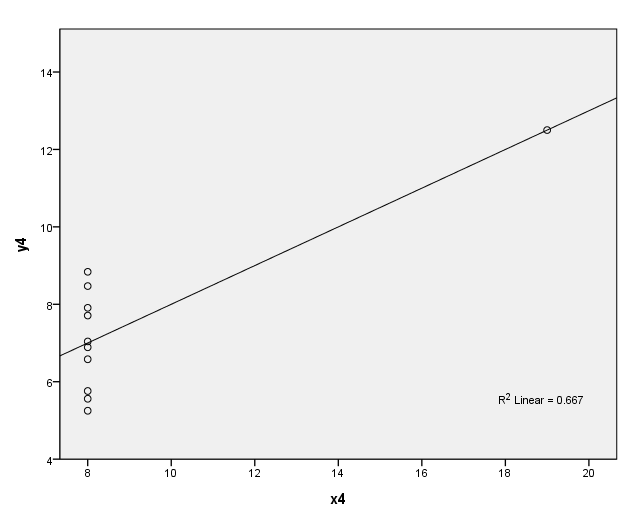
Table 2.5, page 27 length of service calls (in minutes) and number of units repaired
get file 'D:p027.sav'. list.
minutes units
23 1
29 2
49 3
64 4
74 4
87 5
96 6
97 6
109 7
119 8
149 9
145 9
154 10
166 10
Number of cases read: 14 Number of cases listed: 14
Table 2.6, Page 28: Quantities needed for the computation of the correlation
coefficient between the
length of service calls, Y and the number of units repaired, X
compute const = 1.
exe.
aggregate outfile "d:p027ag.sav"
/break =const
/ymean = mean(minutes)
/xmean = mean(units).
match files file = *
/table = "d:p027ag.sav"
/by const.
exe.
compute yd = minutes - ymean.
compute xd = units - xmean.
compute yd2 = yd**2.
compute xd2 = xd**2.
compute xyd = xd*yd.
exe.
list minutes units yd to xyd.
minutes units yd xd yd2 xd2 xyd
23 1 -74.21 -5.00 5507.76 25.00 371.07
29 2 -68.21 -4.00 4653.19 16.00 272.86
49 3 -48.21 -3.00 2324.62 9.00 144.64
64 4 -33.21 -2.00 1103.19 4.00 66.43
74 4 -23.21 -2.00 538.90 4.00 46.43
87 5 -10.21 -1.00 104.33 1.00 10.21
96 6 -1.21 .00 1.47 .00 .00
97 6 -.21 .00 .05 .00 .00
109 7 11.79 1.00 138.90 1.00 11.79
119 8 21.79 2.00 474.62 4.00 43.57
149 9 51.79 3.00 2681.76 9.00 155.36
145 9 47.79 3.00 2283.47 9.00 143.36
154 10 56.79 4.00 3224.62 16.00 227.14
166 10 68.79 4.00 4731.47 16.00 275.14
Number of cases read: 14 Number of cases listed: 14
descriptive variables = minutes to xyd
/statistics = sum.
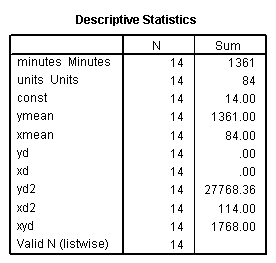
Figure 2.4, page 26 computer repair data: scatter plot of minutes versus units
graph /scatter units with minutes.
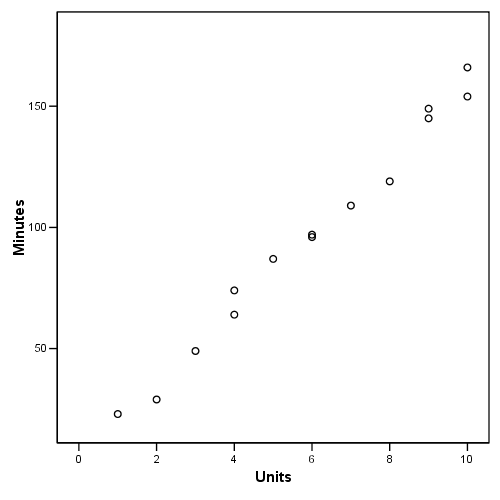
Table 2.7, page 32 the fitted values of, yhat, and the ordinary least squares residuals, e, for the repair data
regression /dependent = minutes /method = enter units /save resid (e) pred (yhat) sepred (semu).
list units yhat e.
units yhat e
1 19.67043 3.32957
2 35.17920 -6.17920
3 50.68797 -1.68797
4 66.19674 -2.19674
4 66.19674 7.80326
5 81.70551 5.29449
6 97.21429 -1.21429
6 97.21429 -.21429
7 112.72306 -3.72306
8 128.23183 -9.23183
9 143.74060 5.25940
9 143.74060 1.25940
10 159.24937 -5.24937
10 159.24937 6.75063
Number of cases read: 14 Number of cases listed: 14
Figure 2.5, page 32 plot of minutes versus units with the fitted least squares regression line
GGRAPH
/GRAPHDATASET NAME="GraphDataset" VARIABLES= minutes units
/GRAPHSPEC SOURCE=INLINE
INLINETEMPLATE=["<addFitLine type='linear' target='pair'/> "].
BEGIN GPL
SOURCE: s=userSource( id( "GraphDataset" ) )
DATA: minutes=col( source(s), name( "minutes" ) )
DATA: units=col( source(s), name( "units" ) )
GUIDE: axis( dim( 1 ), label( "units" ) )
GUIDE: axis( dim( 2 ), label( "minutes" ) )
ELEMENT: point( position( ( units * minutes ) ) )
END GPL.
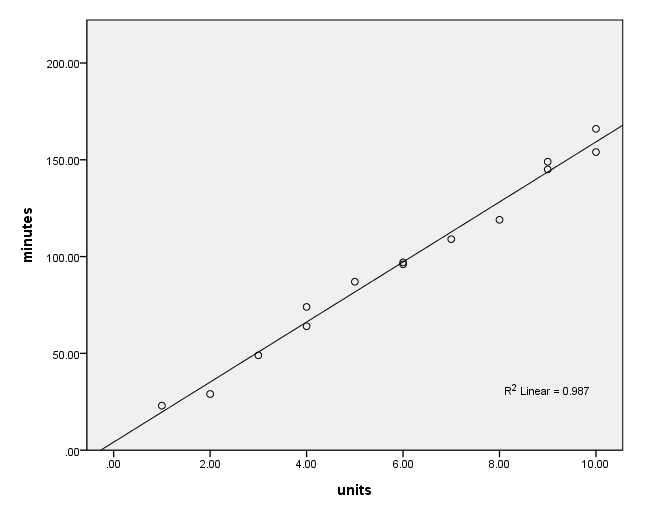
Table 2.8, page 36 regression output for the computer repair data
regression /statistics coef /dependent = minutes /method = enter units.
Standard error for mean prediction, page 39
list units minutes semu.
units minutes semu
1 23 2.90717
2 29 2.48124
3 49 2.09082
4 64 1.75969
4 74 1.75969
5 87 1.52692
6 96 1.44100
6 97 1.44100
7 109 1.52692
8 119 1.75969
9 149 2.09082
9 145 2.09082
10 154 2.48124
10 166 2.48124
Number of cases read: 14 Number of cases listed: 14
Correlations, page 43
correlations variables = minutes units yhat.
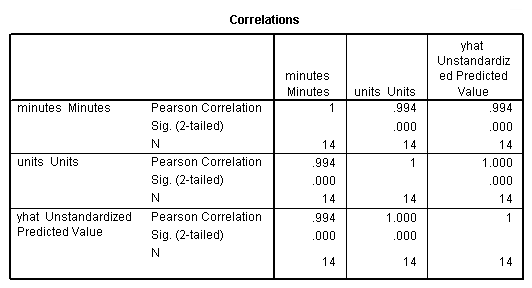
NOTE: (.994)^2 = .987 = R^2
