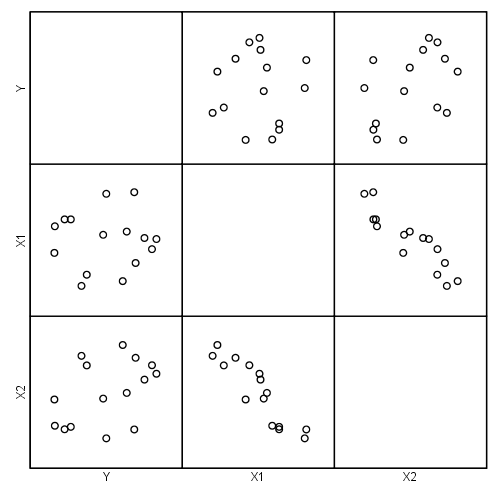
Figure 4.1, page 95 .
Duplicating Figure 2.3 from Chapter 2
get file 'D:p095.sav'.
graph /scatterplot(matrix) = y x1 x2.
correlations variables = y x1 x2.
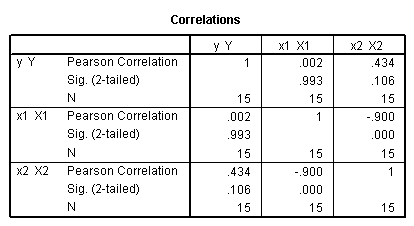
Table 4.2, page 95: Hamilton’s (1987) data
list.
y x1 x2 12.37 2.23 9.66 12.66 2.57 8.94 12.00 3.87 4.40 11.93 3.10 6.64 11.06 3.39 4.91 13.03 2.83 8.52 13.13 3.02 8.04 11.44 2.14 9.05 12.86 3.04 7.71 10.84 3.26 5.11 11.20 3.39 5.05 11.56 2.35 8.51 10.83 2.76 6.59 12.63 3.90 4.90 12.46 3.16 6.96 Number of cases read: 15 Number of cases listed: 15
Regression coefficients for page 95.
regression /dependent = y /method enter = x1.


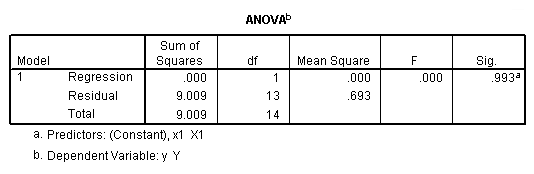
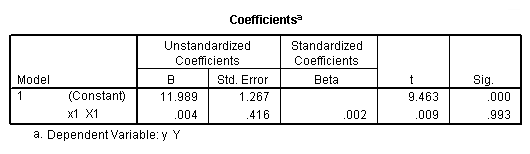
regression /dependent = y /method enter = x2.


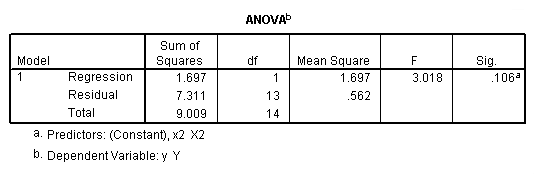
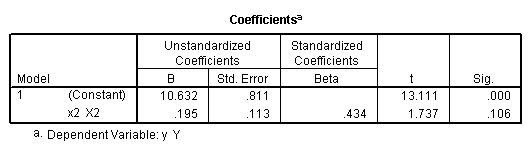
regression /dependent = y /method enter = x1 x2.


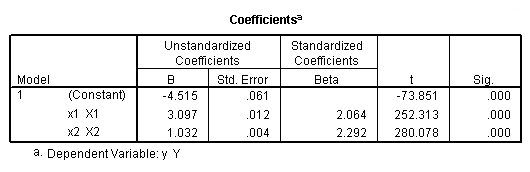
Table 4.2, page 99: New York Rivers Data: The t-test for the individual coefficients. None of the observations deleted.
get file 'D:p010.sav'.
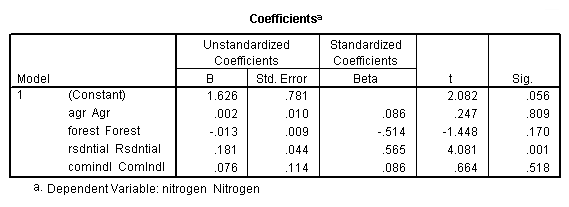
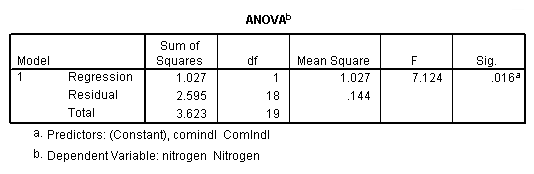
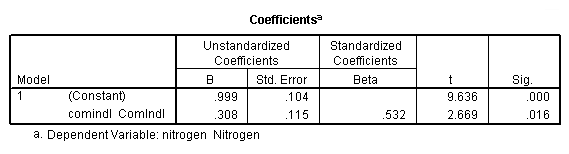
regression /dependent = nitrogen /method enter = agr forest rsdntial comindl.

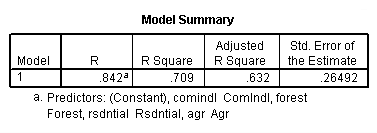
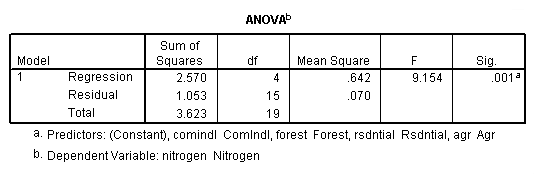
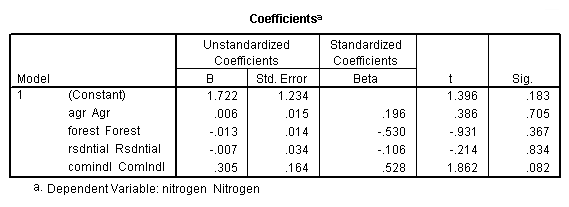
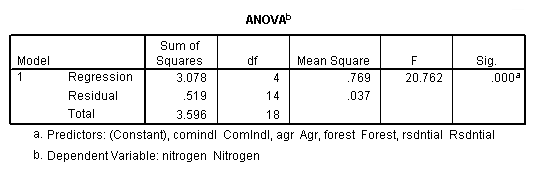
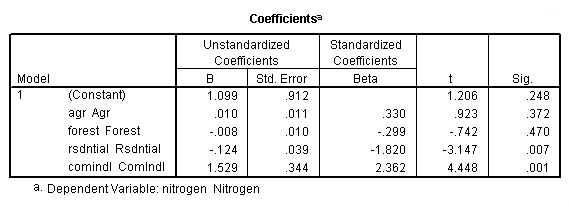
Neversink deleted.
temporary. select if (river ~= "Neversink"). regression /dependent = nitrogen /method enter = agr forest rsdntial comindl.

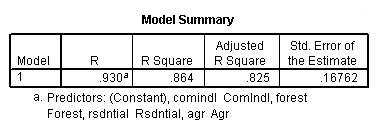
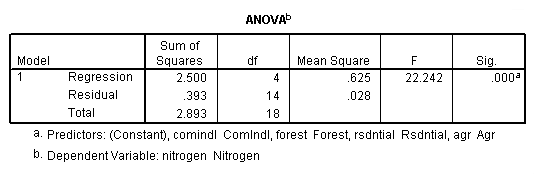
Hackensack deleted
temporary. select if (river ~= "Hackensack"). regression /dependent = nitrogen /method enter = agr forest rsdntial comindl.

Equation (4.18), page 102: also generate the residual and leverage for Table 4.3 and Figure 4.6
regression /dependent = nitrogen /method enter = comindl /save sresid(ri) lever(pi).


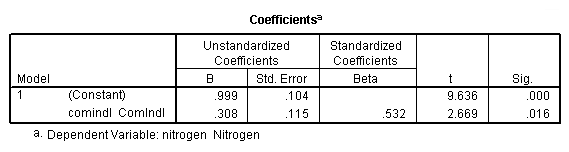
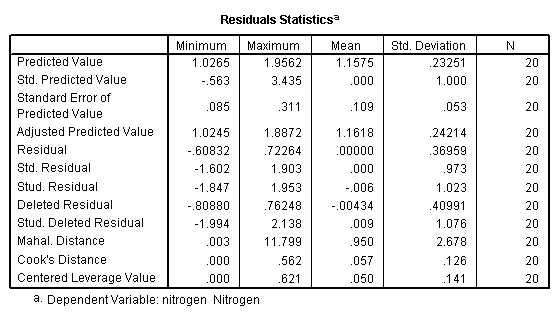
Figure 4.5, page 102: New York Rivers Data: Scatter plot of Y versus X4
compute i = $casenum. exe. formats i (f2.0).
GGRAPH
/GRAPHDATASET NAME="GraphDataset" VARIABLES= nitrogen comindl i
/GRAPHSPEC SOURCE=INLINE
INLINETEMPLATE=["<addFitLine type='linear' target='pair'/> " ].
BEGIN GPL
SOURCE: s=userSource( id( "GraphDataset" ) )
DATA: nitrogen=col( source(s), name( "nitrogen" ) )
DATA: comindl=col( source(s), name( "comindl" ) )
DATA: PointLabel = col( source(s), name( "i" ), unit.category() )
GUIDE: axis( dim( 1 ), label( "comindl" ) )
GUIDE: axis( dim( 2 ), label( "nitrogen" ) )
SCALE: linear( dim( 1 ), min(0.1), max(3.1) )
SCALE: linear( dim( 2 ), min(0.5), max(2.5) )
ELEMENT: point( position( comindl * nitrogen ), label( PointLabel ) )
END GPL.
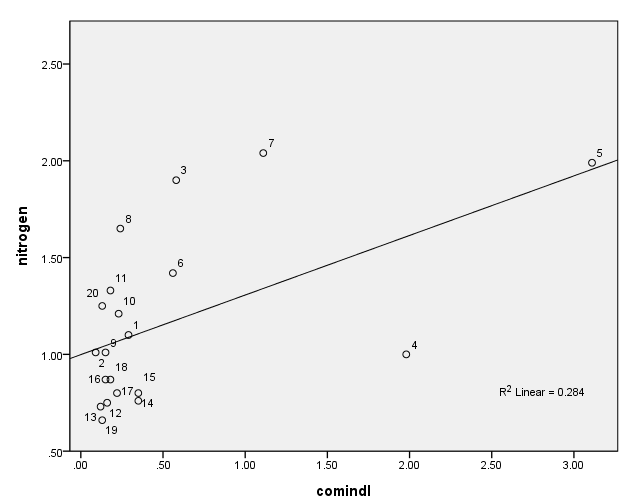
Table 4.3, page 103: New York Rivers Data: The standardized residuals, ri, and the leverage values, pii from fitting model 4.18.
NOTE: The leverage values do not match the book since they are calculated as the centered leverage values.
list i ri pi.
i ri pi
1.00 .03228 .00469
2.00 -.04502 .01670
3.00 1.95292 .00038
4.00 -1.84723 .19787
5.00 .15529 .62101
6.00 .67231 .00018
7.00 1.92326 .03261
8.00 1.56562 .00700
9.00 -.09515 .01232
10.00 .38082 .00752
11.00 .74924 .01038
12.00 -.81033 .01166
13.00 -.83246 .01443
14.00 -.82939 .00253
15.00 -.93761 .00253
16.00 -.47590 .01232
17.00 -.72323 .00806
18.00 -.50049 .01038
19.00 -1.03103 .01371
20.00 .57473 .01371
Number of cases read: 20 Number of cases listed: 20
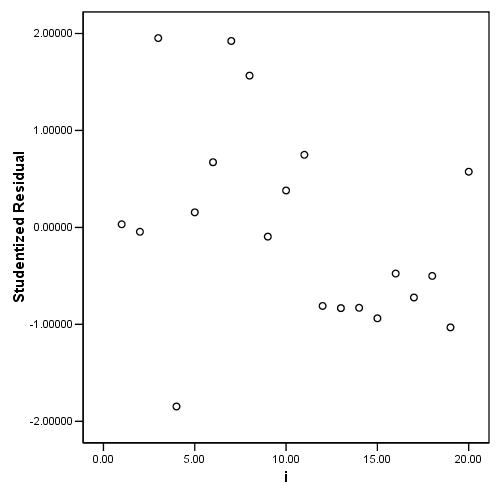
Figure 4.6, page 103: Index plots of (a) the standardized residuals, ri and (b) the leverage values pi.
(a)
graph /scatterplot= i with ri.
(b)
graph /scatterplot = i with pi.
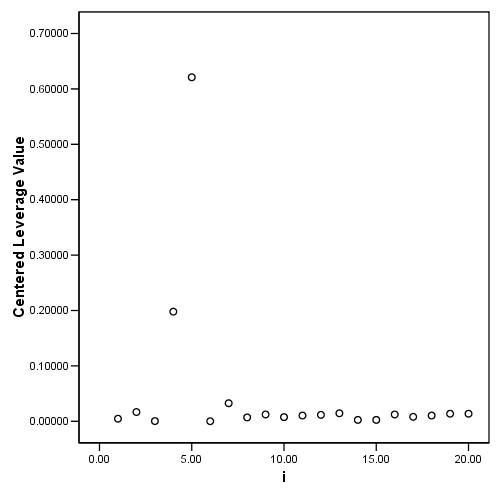
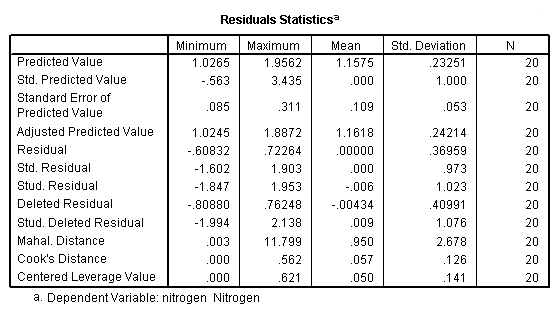
Table 4.4 and Figure 4.7 page 106
regression /dependent = nitrogen /method enter = comindl /save cook(c) dffit(dfits) resid(e).


Compute hadi. Since hadi is constructed using the leverage and not getting accurate leverage numbers, not calculating hadi.
compute d = e/1.6110. compute hadi = (pi/(1-pi)) +((2)/(1-pi))*(d**2/(1-d**2)) . exe. list i c dfits hadi.
i c dfits hadi
1.00 .00003 .00069 .00
2.00 .00007 -.00118 .02
3.00 .10118 .03834 .50
4.00 .56225 -.20047 .66
5.00 .02459 .06898 1.64
6.00 .01194 .01315 .05
7.00 .16653 .06299 .51
8.00 .07408 .03490 .30
9.00 .00030 -.00233 .01
10.00 .00443 .00857 .02
11.00 .01804 .01772 .07
12.00 .02157 -.01959 .08
13.00 .02386 -.02106 .09
14.00 .01907 -.01699 .08
15.00 .02437 -.01921 .10
16.00 .00753 -.01163 .04
17.00 .01612 -.01643 .06
18.00 .00805 -.01184 .04
19.00 .03617 -.02578 .13
20.00 .01124 .01437 .05
Number of cases read: 20 Number of cases listed: 20
graph (a)
graph /scatterplot = i with c.
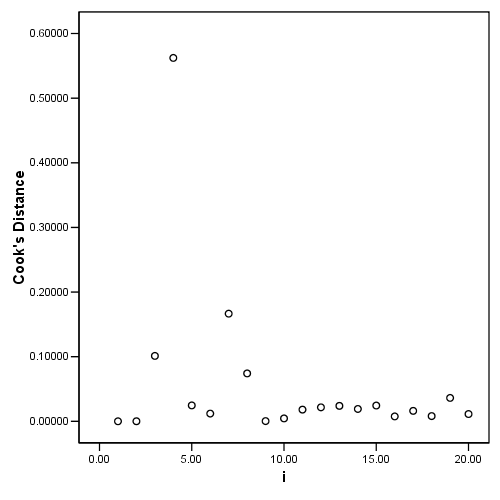
graph (b)
graph /scatterplot = i with dfits.
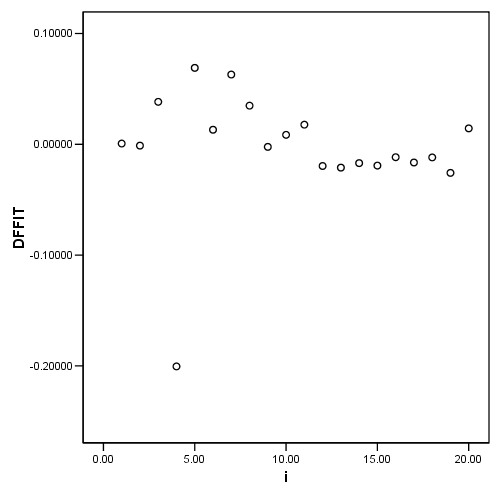
graph (c)
graph /scatterplot = i with hadi.
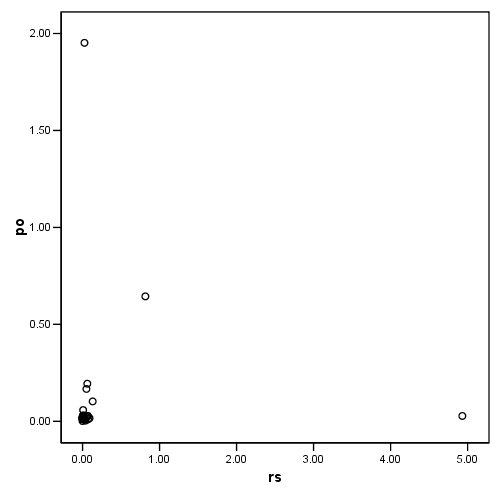
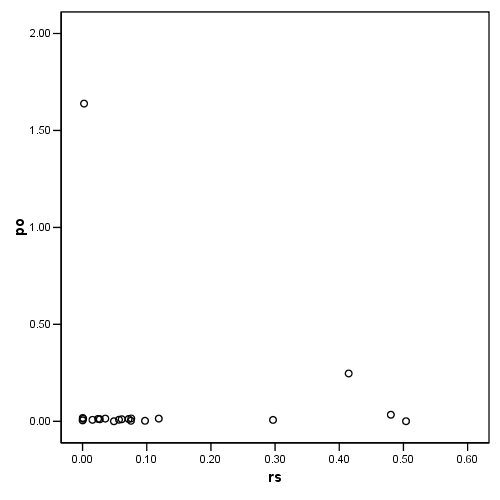
Figure 4.8, page 108: Potential-Residual Plot
compute po = (pi/(1-pi)). compute rs = ((2)/(1-pi))*(d**2/(1-d**2)). exe. graph /scatterplot = rs with po.
Equation (4.25), bottom of page 111
get file 'D:p112.sav'.
regression /dependent = time /method enter = distance climb.


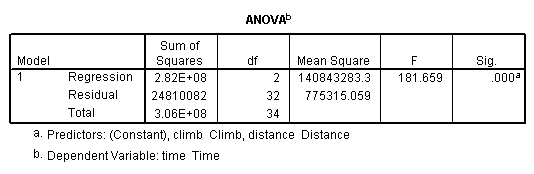
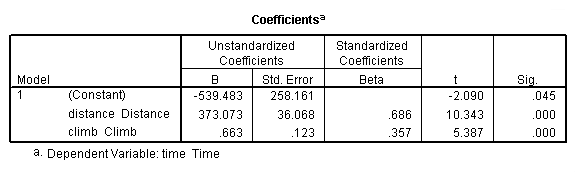
Table 4.5, page 112: Scottish Hills Race Data
list. hillrace time distance climb Greenmantle New Year Dash 965 2.50 650 Carnethy 2901 6.00 2500 Craig Dunain 2019 6.00 900 Ben Rha 2736 7.50 800 Ben Lomond 3736 8.00 3070 Goatfell 4393 8.00 2866 Bens of Jura 12277 16.00 7500 Cairnpapple 2182 6.00 800 Scolty 1785 5.00 800 Traprain Law 2385 6.00 650 Lairig Ghru 11560 28.00 2100 Dollar 2583 5.00 2000 Lomonds of Fife 3900 9.50 2200 Cairn Table 2648 6.00 500 Eildon Two 1616 4.50 1500 Cairngorm 4335 10.00 3000 Seven Hills of Edinburgh 5905 14.00 2200 Knock Hill 4719 3.00 350 Black Hill 1045 4.50 1000 Creag Beag 1954 5.50 600 Kildoon 957 3.00 300 Meall Ant-Suiche 1674 3.50 1500 Half Ben Nevis 2859 6.00 2200 Cow Hill 1076 2.00 900 North Berwick Law 1121 3.00 600 Creag Dubh 1573 4.00 2000 Burnswark 2066 6.00 800 Largo 1714 5.00 950 Criffel 3030 6.50 1750 Achmony 1257 5.00 500 Ben Nevis 5135 10.00 4400 Knockfarrel 1943 6.00 600 Two Breweries Fell 10215 18.00 5200 Cockleroi 1686 4.50 850 Moffat Chase 9590 20.00 5000 Number of cases read: 35 Number of cases listed: 35
Figure 4.10, page 113. Rotating plot for the Scottish Hills Race Data
compute id = $casenum. exe. formats id (f2.0).
GGRAPH
/GRAPHDATASET NAME="GraphDataset" VARIABLES= time distance climb id
/GRAPHSPEC SOURCE=INLINE
INLINETEMPLATE=["<addDataLabels><labeling variable='percent'><format suffix='%'/></labeling></addDataLabels>"].
BEGIN GPL
SOURCE: s=userSource( id( "GraphDataset" ) )
DATA: time=col( source(s), name( "time" ) )
DATA: distance=col( source(s), name( "distance" ) )
DATA: climb=col( source(s), name( "climb" ) )
DATA: id = col( source(s), name( "id" ), unit.category() )
COORD: rect( dim( 1,2,3 ) )
GUIDE: axis( dim( 1 ), label( "climb" ), start(0.0), delta(8000))
GUIDE: axis( dim( 2 ), label( "distance" ), start(0.0), delta(30) )
GUIDE: axis( dim( 3 ), label( "time" ), start(0.0), delta(12000) )
SCALE: linear( dim( 1 ), min(0), max(8000) )
SCALE: linear( dim( 2 ), min(0), max(30) )
SCALE: linear( dim( 3 ), min(0), max(12000) )
ELEMENT: point( position( ( climb * distance * time ) ), label( id ) )
END GPL.
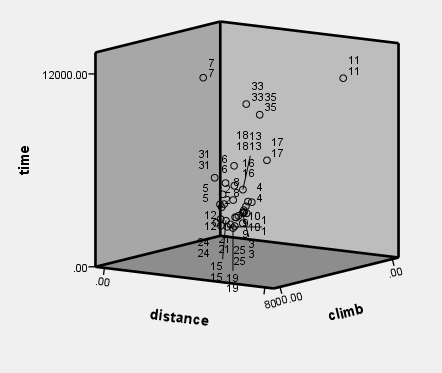
Figure 4.11, page 114. Added-variable plots for (a) distance and (b) climb
regression /dependent = time /method enter = distance climb /partialplot all /save resid(e) lever(pi).

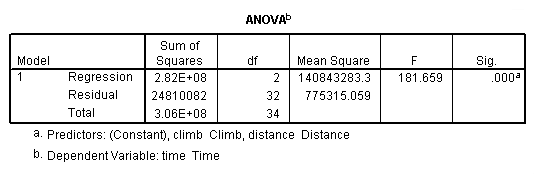
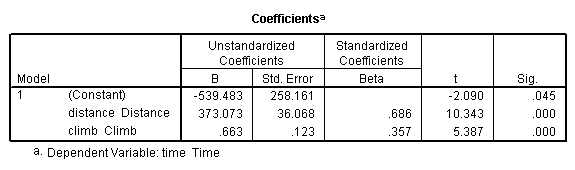

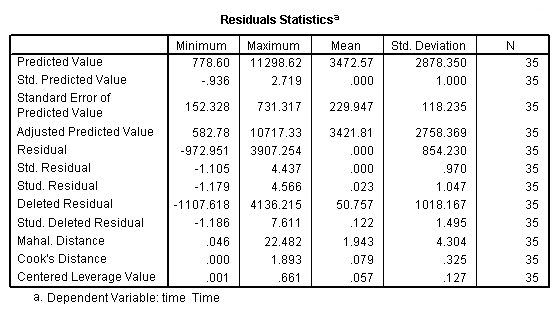
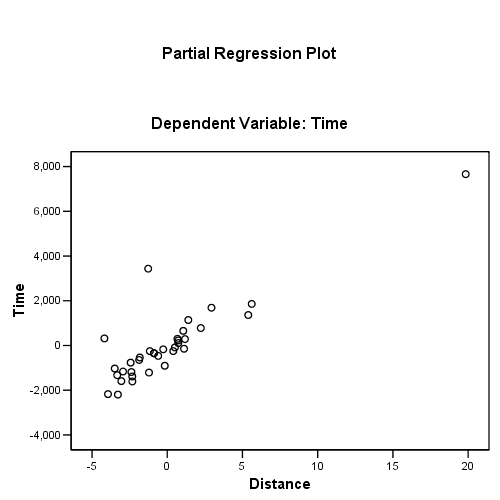
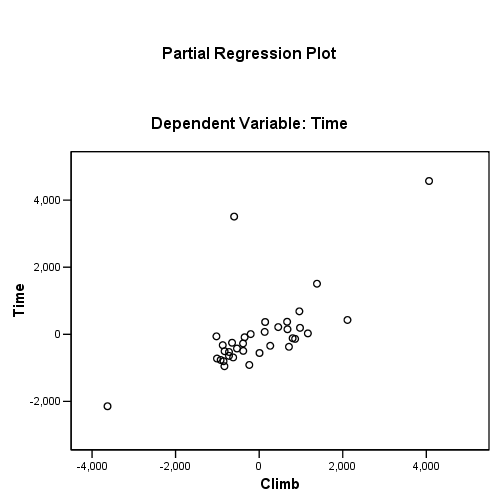
using the regression coefficients for calculating the residual plus component plot
compute rpc_dist = e + 373.073*distance. compute rpc_climb = e + .663*climb. exe.
Figure 4.12(a), page 114
Note: The graph in the book is incorrect; please see errata.
graph /scatterplot = distance with rpc_dist.
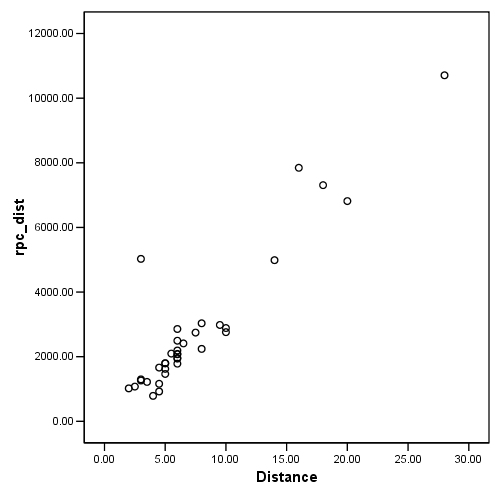
Figure 4.12(b), page 114
Note: The graph in the book is incorrect; please see errata.
graph /scatterplot = climb with rpc_climb.
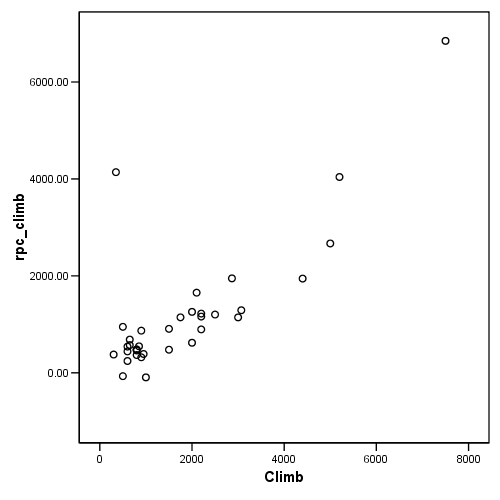
Figure 4.13, page 114. Potential-Residual plot
compute d = e/sqrt(24810082). compute po = (pi/(1-pi)). compute rs = ((3)/(1-pi))*(d**2/(1-d**2)). exe. graph /scatterplot = rs with po.