Many data sets have missing values. However, having lots of missing values can be problematic, as most statistical procedures (e.g., regression) will do a casewise deletion of cases with missing values. This means that the procedure works runs on only the cases with complete data, and that may be a fraction of the cases in the data set. Hence, finding out the number of missing values each variable has can be important. Let’s look at the following data set.
LANDVAL IMPROVAL TOTVAL SALEPRIC SALTOAPR
30000 64831 94831 118500 1.25
30000 50765 80765 93900 .
46651 18573 65224 . 1.16
45990 91402 . 184000 1.34
42394 . 40575 168000 1.43
. 3351 51102 169000 1.12
63596 2182 65778 . 1.26
56658 53806 10464 255000 1.21
51428 72451 . . 1.18
93200 . 4321 422000 1.04
76125 78172 54297 290000 1.14
. 61934 16294 237000 1.10
65376 34458 . 286500 1.43
42400 . 57446 . .
40800 92606 33406 168000 1.26
1. Number of missing values versus number of non-missing values
The first thing to do is find out how many missing values each variable has. We can use the frequencies command with the format=notable subcommand.
FREQUENCIES VARIABLES=landval improval totval salepric saltoapr /FORMAT=NOTABLE /ORDER= ANALYSIS .

Now we know the number of missing values in each variable: the variable salepric has four and saltoapr has two missing values. This will help us to identify variables that may have a large number of missing values, and perhaps we may want exclude those from analysis.
2. Number of missing values in each observation
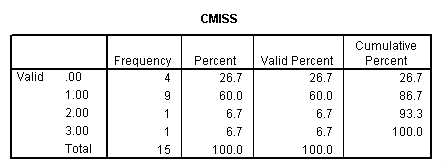
We can also look at the distribution of missing values across observations. For example we use the count command to create a new variable called cmiss, which counts the number of missing values across each observation. Looking at its frequency table, we know that there are four observations with no missing values, nine observations with one missing value, one observation with two missing values and one observation with three missing values.
COUNT cmiss = landval improval totval salepric saltoapr (MISSING). FREQUENCIES VARIABLES=cmiss /ORDER= ANALYSIS .
3. Patterns of missing values
We can also look at the patterns of missing values. We can recode each variable into a dummy variable such that 1 is missing and 0 is non-missing. Then we use the aggregate command to compute the frequency for each pattern of missing data.
RECODE landval improval totval salepric saltoapr (MISSING=1) (ELSE=0) INTO land1 impr1 totv1 sale1 salt1 . AGGREGATE /OUTFILE='AGGR.SAV' /BREAK=land1 impr1 totv1 sale1 salt1 /N_BREAK=N.File AGGR.SAV has the following variables and observations.LAND1 IMPR1 TOTV1 SALE1 SALT1 N_BREAK .00 .00 .00 .00 .00 4 .00 .00 .00 .00 1.00 1 .00 .00 .00 1.00 .00 2 .00 .00 1.00 .00 .00 2 .00 .00 1.00 1.00 .00 1 .00 1.00 .00 .00 .00 2 .00 1.00 .00 1.00 1.00 1 1.00 .00 .00 .00 .00 2
Now we see that there are four observations with no missing values, one observation with one missing value in variable saltoapr, two observations with missing value in variable salepric and one observation with missing values in both variable totval and salepric, etc.
