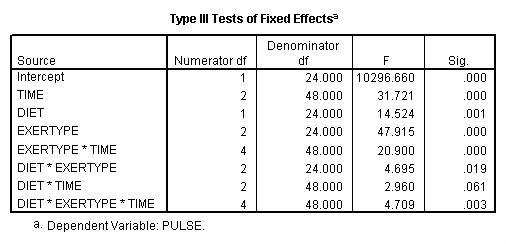
It can be rather tricky to program the test subcommand when there are higher order interactions (e.g., three-way interactions, four-way interactions, etc.) included in the mixed model. Let’s look at an example where we are using the mixed command in a repeated measures model. The data set exercise was used in our seminar on repeated measures. The data set consists of people who were randomly assigned to two different diets: low-fat and not low-fat, as well as three different types of exercise: at rest, walking leisurely and running. Their pulse rate was measured at three different time points during their assigned exercise: at 1 minute, 15 minutes and 30 minutes. We included all three variables in our mixed model: diet which has two levels, exertype which has three levels and time which also has three levels. Even though time is a repeated factor we can treat it in the same manner as the other variables when we want to test the various contrasts and interaction contrasts that may be of interest. Finally, we will present an example of how to program the test subcommand for interaction contrasts involving a three-way interaction.
Contrasts for one variable
mixed pulse by diet exertype time /fixed = time diet exertype /repeated = time | subject(id) covtype(arh1) /test = 'exertype 12v3' exertype -.5 -.5 1.
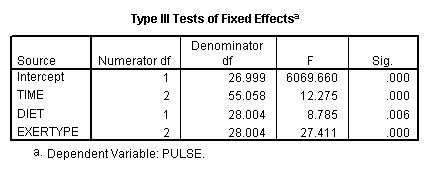
Let’s look at an example where the mixed model includes only the main effects of diet, exertype and time. From the graph we see that there might be a difference between exertype level 3 and the two other levels of exertype. Therefore, we will use a reverse Helmert coding for exertype in the test subcommand in order to test this particular contrast. For more information on reverse Helmert coding and other contrast coding systems please refer to chapter 5 in our webbook on regression.
The contrast coding:
|
exertype level 1 |
-1/2 |
|
exertype level 2 |
-1/2 |
|
exertype level 3 |
1 |
mixed pulse by diet exertype time /fixed = time diet exertype /repeated = time | subject(id) covtype(ar1) /test = 'exertype 12v3' exertype -.5 -.5 1.
The two-way model including the interaction of exertype and diet
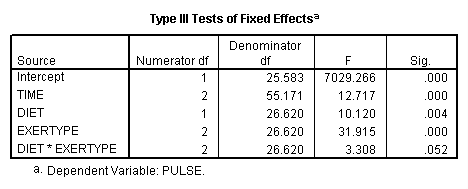
Let us look at testing the same contrast, but this time we will use a different model which will include an interaction between exertype and diet. In order to implement the test of the contrast, we have to introduce the idea of distributing the contrast coding of lower order terms on the higher order terms. In other words, when we have higher order terms which include the term being tested, such as the two-way interaction of exertype and diet, then we need to include these higher order terms in the test subcommand with the appropriate contrast coding as well as the contrast coding for the main effect being tested. The diet*exertype interaction is coded as d1e1 d1e2 d1e3 d2e1 d2e2 d2e3, where d# = coding for diet level # and e# = coding for exertype level # and d#e# is the product of the two. Since we are not contrast coding diet, we just want the “weight” for each level of diet to be equal; hence, we assign both levels of diet the same “weight” of 1/2 because there are two levels of diet. The order of the factors is determined by the order in which they appear in the mixed command. In this particular case, diet appears before exertype in the mixed command, and thus with our coding system for diet and exertype we would have the following coding for the interaction:
d1e1 = 1/2*-1/2 = -1/4 d1e2 = 1/2*-1/2 = -1/4 d1e3 = 1/2*1 = 1/2 d2e1 = 1/2*-1/2 = -1/4 d2e2 = 1/2*-1/2 = -1/4 d2e3 = 1/2*1 = 1/2
In order to more easily understand the coding for the interaction, it might help to visualize it as a matrix which equals the product of the code for diet as a column matrix and the contrast coding of exertype as a row matrix.
| exertype level 1 = -1/2 | exertype level 2 = -1/2 | exertype level 3 = 1 | |
| diet level 1 = 1/2 |
1/2*-1/2 = -1/4 |
1/2*-1/2 = -1/4 |
1/2*1 = 1/2 |
| diet level 2 = 1/2 |
1/2*-1/2 = -1/4 |
1/2*-1/2 = -1/4 |
1/2*1 = 1/2 |
Now the test subcommand will include both exertype with its contrast coding and the interaction of exertype*diet with its contrast coding. Note that the fixed subcommand reflects the change in the model to include the interaction of diet and exertype.
mixed pulse by diet exertype time /fixed = time diet exertype diet*exertype /repeated = time | subject(id) covtype(ar1) /test = 'exertype 12v3' exertype -.5 -.5 1 diet*exertype -1/4 -1/4 1/2 -1/4 -1/4 1/2.
The three-way model including the interaction of exertype*time and the three-way interaction
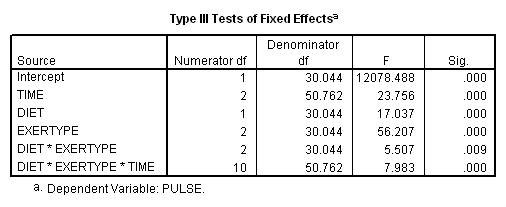
Let’s consider testing the same contrast for exertype but using a model that includes the interaction of exertype and time as well as the three-way interaction of diet*exertype*time. In this case we will need to include three terms in our test subcommand: the main effect of exertype, the interaction diet*exertype and the three-way interaction diet*exertype*time, each with their appropriate contrast coding. The coding of exertype will be the same as in the one-way example.
The exertype*time interaction is coded as e1t1 e1t2 e1t3 e2t1 e2t2 e2t3 e3t1 e3t2 e3t3, where e# = coding for exertype level # and t# = coding for time level # and e#t# is the product of the two. Since we are not contrast coding time, we just want the “weight” for each level of time to be equal; hence, we assign all three levels of time the same “weight” of 1/3. The order of the factors is determined by the order in which they appear in the mixed command. In this particular case exertype appears before time in the mixed command, and thus with our coding system for exertype and time we would have the following coding for the interaction:
e1t1 = 1/3*-1/2 = -1/6 e1t2 = 1/3*-1/2 = -1/6 e1t3 = 1/3*-1/2 = -1/6 e2t1 = 1/3*-1/2 = -1/6 e2t2 = 1/3*-1/2 = -1/6 e2t3 = 1/3*-1/2 = -1/6 e3t1 = 1/3*1 = 1/3 e3t2 = 1/3*1 = 1/3 e3t3 = 1/3*1 = 1/3
In order to more easily understand the coding for the interaction, it might help to visualize it as a matrix which equals the product of the contrast code for exertype as a column matrix and the coding of time as a row matrix.
| time level 1 = 1/3 | time level 2 = 1/3 | time level 3 = 1/3 | |
| exertype level 1 = -1/2 |
1/3*-1/2 = -1/6 |
1/3*-1/2 = -1/6 |
1/3*-1/2 = -1/6 |
| exertype level 2 = -1/2 |
1/3*-1/2 = -1/6 |
1/3*-1/2 = -1/6 |
1/3*-1/2 = -1/6 |
| exertype level 3 = 1 |
1/3*1 = 1/3 |
1/3*1 = 1/3 |
1/3*1 = 1/3 |
The contrast coding for the three-way interaction is slightly more complicated. The diet*exertype*time interaction is coded as d1e1t1 d1e1t2 d1e1t3 d1e2t1 d1e2t2 d1e2t3 d1e3t1 d1e3t2 d1e3t3 d2e1t1 d2e1t2 d2e1t3 d2e2t1 d2e2t2 d2e2t3 d2e3t1 d2e3t2 d2e3t3. For this code d# = coding for diet level #, e# = coding for exertype level #, t# = coding for time level # and d#e#t# is the product of the three. Since we are only contrasting levels of exertype and not levels of either diet or time, we want to code each level of diet to be “weighted” equally, so they are both coded as 1/2; likewise, we want to code each level of time to be “weighted” equally, so all three levels of time are coded as 1/3. In this case the coding for the interaction is:
d1e1t1 = 1/2*-1/2*1/3 = -1/12 d1e1t2 = 1/2*-1/2*1/3 = -1/12
d1e1t3 = 1/2*-1/2*1/3 = -1/12 d1e2t1 = 1/2*-1/2*1/3 = -1/12
d1e2t2 = 1/2*-1/2*1/3 = -1/12 d1e2t3 = 1/2*-1/2*1/3 = -1/12
d1e3t1 = 1/2*1*1/3 = 1/6 d1e3t2 = 1/2*1*1/3 = 1/6 d1e3t3 = 1/2*1*1/3 = 1/6
d2e1t1 = 1/2*-1/2*1/3 = -1/12 d2e1t2 = 1/2*-1/2*1/3 = -1/12 d2e1t3 = 1/2*-1/2*1/3 = -1/12 d2e2t1 = 1/2*-1/2*1/3 = -1/12 d2e2t2 = 1/2*-1/2*1/3 = -1/12 d2e2t3 = 1/2*-1/2*1/3 = -1/12 d2e3t1 = 1/2*1*1/3 = 1/6 d2e3t2 = 1/2*1*1/3 = 1/6
d2e3t3 = 1/2*1*1/3 = 1/6
This can be more conveniently visualized as matrices. The coding for time, which is the last factor in the mixed command, can be thought of as the row matrix that is multiplied by the coding for exertype which is the second to last factor in the mixed command and which can be thought of as the column matrix. The matrix which is the product is then multiplied by the coding for each level of diet which appears before exertype and time in the mixed command.
For diet level 1 = 1/2:
| time level 1 = 1/3 | time level 2 = 1/3 | time level 3 = 1/3 | |
| exertype level 1 = -1/2 | 1/2*-1/2*1/3 = -1/12 | 1/2*-1/2*1/3 = -1/12 | 1/2*-1/2*1/3 = -1/12 |
| exertype level 2 = -1/2 | 1/2*-1/2*1/3 = -1/12 | 1/2*-1/2*1/3 = -1/12 | 1/2*-1/2*1/3 = -1/12 |
| exertype level 3 = 1 | 1/2*1*1/3 = 1/6 | 1/2*1*1/3 = 1/6 | 1/2*1*1/3 = 1/6 |
For diet level 2 = 1/2:
| time level 1 = 1/3 | time level 2 = 1/3 | time level 3 = 1/3 | |
| exertype level 1 = -1/2 | 1/2*-1/2*1/3 = -1/12 | 1/2*-1/2*1/3 = -1/12 | 1/2*-1/2*1/3 = -1/12 |
| exertype level 2 = -1/2 | 1/2*-1/2*1/3 = -1/12 | 1/2*-1/2*1/3 = -1/12 | 1/2*-1/2*1/3 = -1/12 |
| exertype level 3 = 1 | 1/2*1*1/3 = 1/6 | 1/2*1*1/3 = 1/6 | 1/2*1*1/3 = 1/6 |
mixed pulse by diet exertype time /fixed = time diet exertype diet*exertype diet*exertype*time /repeated = time | subject(id) covtype(ar1) /test = 'exertype 12v3' exertype -.5 -.5 1 diet*exertype -1/4 -1/4 1/2 -1/4 -1/4 1/2 diet*exertype*time -1/12 -1/12 -1/12 -1/12 -1/12 -1/12 1/6 1/6 1/6 -1/12 -1/12 -1/12 -1/12 -1/12 -1/12 1/6 1/6 1/6.
Interaction contrasts
The model including only two-way interactions
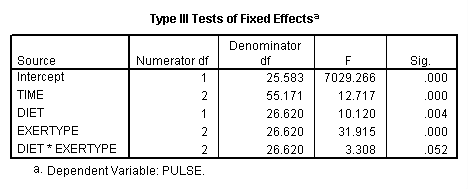
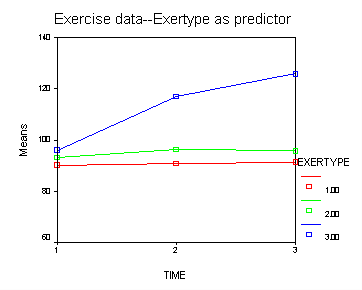
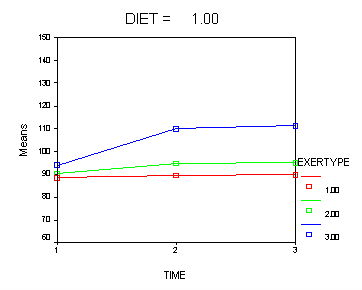
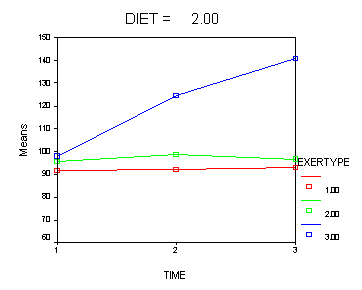
Let’s consider an interaction contrast involving diet and exertype in a mixed model which includes diet, exertype, time and all the two-way interactions. From the graphs we see that exertype level 3 is higher than both levels 1 and 2 for both diets but that level 3 increases at different rates depending on which diet is considered. We would like to contrast exertype level 3 in diet 2 with the other groups in order to see if they are really different from the other groups. In order to accomplish, this we will need to use an interaction contrast where exertype is coded with a reverse Helmert coding contrasting level three versus levels 1 and 2 and diet has a contrasts coding contrasting level1 versus level 2. For more information on reverse Helmert coding and other contrast coding systems please refer to chapter 5 in our webbook on regression.
The contrast coding:
|
exertype level 1 |
-1/2 |
|
exertype level 2 |
-1/2 |
|
exertype level 3 |
1 |
|
diet level 1 |
1 |
|
diet level 2 |
-1 |
The diet*exertype interaction is coded as d1e1 d1e2 d1e3 d2e1 d2e2 d2e3, where d# = coding for diet level # and e# = coding for exertype level # and d#e# is the product of the two. The contrast coding for diet is level 1 = 1 and level 2 = -1 and the contrast coding for exertype is the same as in the previous example, namely, level 1 = -1/2, level 2 = -1/2 and level 3 = 1. The order of the factors is determined by the order in which they appear in the mixed command. In this particular case diet appears before exertype in the mixed command, and thus with our coding system for diet and exertype, we would have the following coding for the interaction:
d1e1 = 1*-1/2 = -1/2 d1e2 = 1*-1/2 = -1/2 d1e3 = 1*1 = 1 d2e1 = -1*-1/2 = 1/2 d2e2 = -1*-1/2 = 1/2 d2e3 = -1*1 = -1
In order to more easily understand the coding for the interaction, it might help to visualize it as a matrix which equals the product of the code for diet as a column matrix and the contrast coding of exertype as a row matrix.
| exertype level 1 = -1/2 | exertype level 2 = -1/2 | exertype level 3 = 1 | |
| diet level 1 = 1 |
1*-1/2 = -1/2 |
1*-1/2 = -1/2 |
1*1 = 1 |
| diet level 2 = -1 |
-1*-1/2 = 1/2 |
-1*-1/2 = 1/2 |
-1*1 = -1 |
We don’t need to include any other terms besides the interaction diet*exertype since the model does not include any higher order terms that contain diet*exertype. If a term, such as the interaction exertype*time, contains only part of the interaction being tested, then it is not included in the test subcommand. Only those higher order terms, which contain the complete term diet*exertype being tested are included.
mixed pulse by diet exertype time /fixed = diet exertype time diet*exertype /repeated = time | subject(id) covtype(ar1) /test = 'exertype 12v3 & diet 1v2' diet*exertype -.5 -.5 1 .5 .5 -1.
Let’s test the same interaction contrast but now we will consider a model that includes all two-way interactions and the three-way interaction. Just as in the previous example we now have to “distribute” the contrast coding of the lower order term across the higher order terms. In other words, the test subcommand will include the contrast coding for the interaction of diet*exertype that we developed in the above example. We also have to include the three-way interaction with the appropriate contrast coding because the three-way interaction includes the term, namely diet*exertype, being tested.
The contrast coding for the three-way interaction is slightly more complicated. The diet*exertype*time interaction is coded as d1e1t1 d1e1t2 d1e1t3 d1e2t1 d1e2t2 d1e2t3 d1e3t1 d1e3t2 d1e3t3 d2e1t1 d2e1t2 d2e1t3 d2e2t1 d2e2t2 d2e2t3 d2e3t1 d2e3t2 d2e3t3. In this code, d# = coding for diet level #, e# = coding for exertype level #, t# = coding for time level # and d#e#t# is the product of the three. The contrast coding for exertype is level 1 = -1/2, level 2 = -1/2 and level 3 = 1; the contrast coding for diet is level 1 = 1 and level 2 = -1. Since we are not implementing a contrast for time we want to code each level of time to be “weighted” equally, so all three levels are coded as 1/3. Note that the coding is very similar to the second example in the contrast section of this FAQ, but that instead of coding diet as 1/2 for each level, we are now giving diet a contrast coding because we are testing in interaction contrast. In this case the coding for the interaction is:
d1e1t1 = 1*-1/2*1/3 = -1/6 d1e1t2 = 1*-1/2*1/3 = -1/6 d1e1t3 = 1*-1/2*1/3 = -1/6 d1e2t1 = 1*-1/2*1/3 = -1/6 d1e2t2 = 1*-1/2*1/3 = -1/6 d1e2t3 = 1*-1/2*1/3 = -1/6 d1e3t1 = 1*1*1/3 = 1/3 d1e3t2 = 1*1*1/3 = 1/3 d1e3t3 = 1*1*1/3 = 1/3
d2e1t1 = -1*-1/2*1/3 = 1/6 d2e1t2 = -1*-1/2*1/3 = 1/6 d2e1t3 = -1*-1/2*1/3 = 1/6 d2e2t1 = -1*-1/2*1/3 = 1/6 d2e2t2 = -1*-1/2*1/3 = 1/6 d2e2t3 = -1*-1/2*1/3 = 1/6 d2e3t1 = -1*1*1/3 = –1/3 d2e3t2 = -1*1*1/3 = –1/3 d2e3t3 = -1*1*1/3 = –1/3
This can be more conveniently visualized as matrices. The coding for time which is the last factor in the mixed command can be thought of as the row matrix that is multiplied by the coding for exertype which is the second to last factor in the mixed command and which can be thought of as the column matrix. The matrix which is the product is then multiplied by the coding for each level of diet which appears before exertype and time in the mixed command.
For diet level 1 = 1:
| time level 1 = 1/3 | time level 2 = 1/3 | time level 3 = 1/3 | |
| exertype level 1 = -1/2 | 1*-1/2*1/3 = -1/6 | 1*-1/2*1/3 = -1/6 | 1*-1/2*1/3 = -1/6 |
| exertype level 2 = -1/2 | 1*-1/2*1/3 = -1/6 | 1*-1/2*1/3 = -1/6 | 1*-1/2*1/3 = -1/6 |
| exertype level 3 = 1 | 1*1*1/3 = 1/3 | 1*1*1/3 = 1/3 | 1*1*1/3 = 1/3 |
For diet level 2 = -1:
| time level 1 = 1/3 | time level 2 = 1/3 | time level 3 = 1/3 | |
| exertype level 1 = -1/2 | -1*-1/2*1/3 = 1/6 | -1*-1/2*1/3 = 1/6 | -1*-1/2*1/3 = 1/6 |
| exertype level 2 = -1/2 | -1*-1/2*1/3 = 1/6 | -1*-1/2*1/3 = 1/6 | -1*-1/2*1/3 = 1/6 |
| exertype level 3 = 1 | -1*1*1/3 = –1/3 | -1*1*1/3 = –1/3 | -1*1*1/3 = –1/3 |
mixed pulse by diet exertype time /fixed = time diet exertype time*exertype diet*exertype time*diet diet*exertype*time /repeated = time | subject(id) covtype(cs) /test = 'exertype 12v3, diet 1v2' diet*exertype -.5 -.5 1 .5 .5 -1 diet*exertype*time -1/6 -1/6 -1/6 -1/6 -1/6 -1/6 1/3 1/3 1/3 1/6 1/6 1/6 1/6 1/6 1/6 -1/3 -1/3 -1/3.