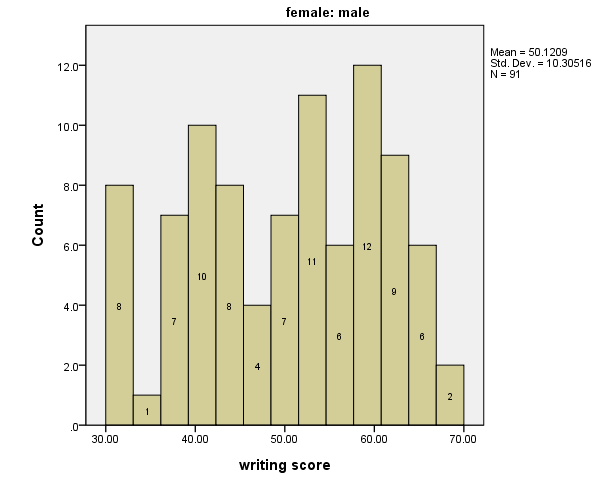
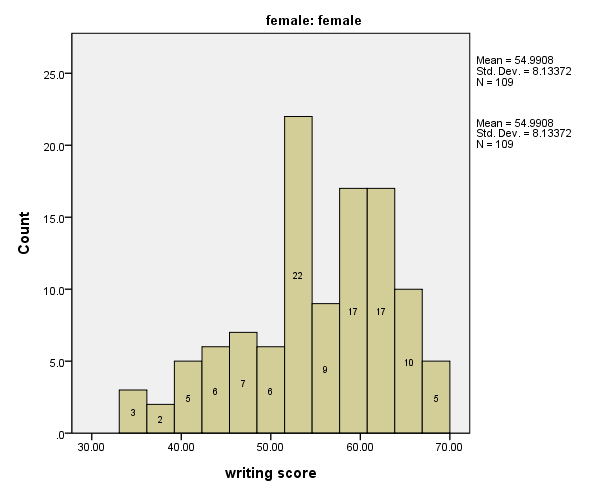
An alternative test to the classic t-test is the Kolmogorov-Smirnov test for equality of distributional functions. In a simple example, we’ll see if the distribution of writing test scores across gender are equal using the hsb2 data set. We’ll first do histograms of writing scores by gender.
get file = 'c:/hsb2.sav'.
sort cases by female.
split file by female.
GGRAPH
/GRAPHDATASET NAME="iGraphDataset" VARIABLES= write
/GRAPHSPEC SOURCE=INLINE
INLINETEMPLATE=["<addDataLabels><labeling variable='percent'></labeling></addDataLabels>"].
BEGIN GPL
SOURCE: s=userSource( id( "iGraphDataset" ) )
DATA: Y_Var=col( source(s), name( "$count" ) )
DATA:write=col( source(s), name( "write" ) )
GUIDE: axis( dim( 1 ), label( "writing score" ) )
GUIDE: axis( dim( 2 ), label( "Count" ) )
ELEMENT: interval( position( summary.count( bin.rect(write * 1, binCount( 13 ) ) ) ) )
END GPL.
split file off. npar test /k-s = write by female(1 0).
From the test (Kolmogorov-Smirnov Z = 1.738, p = .005), it is apparent that the writing scores do not have
the same distributional function across gender.