1. Contrived example, odds ratio of 2
Below we have a data file with information about families containing the husband’s income (in thousands of dollars) ranging from 10,000 to 12,000, and whether the wife works, 1 if the wife does work, and 0 if the wife does not work.
data list list /inc wifework. begin data. 10 0 10 1 10 1 11 0 11 1 11 1 11 1 11 1 12 0 12 1 12 1 12 1 12 1 12 1 12 1 12 1 12 1 end data.
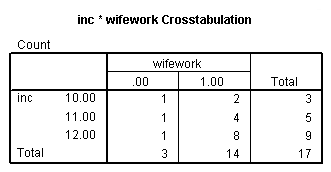
You might notice that for families earning $10,000, there are 2 wives who work and 1 who does not, for families earning $11,000 there are 4 wives who work, and 1 who does not, and for families earning $12,000 there are 8 wives who work, and 1 who does not. We can confirm this using crosstabs.
crosstabs inc by wifework.
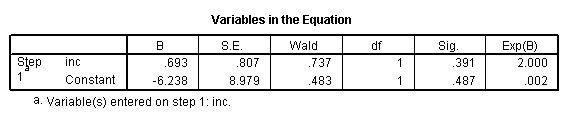
Let’s run a logistic regression predicting wifework from inc. You can see below that the Odds Ratio predicting wifework from inc is 2 (in the right-most column labeled "Exp(B)"). But what does this mean? The definition of an odds ratio tells us that for every unit increase in inc, the odds of the wife working increases by a factor of 2.
logistic regression wifework /method = enter inc.
Let us explore what this means. At the heart of this is the odds ratio, but let’s first start with looking at the odds of the wife working at each level of inc, as shown below.
Number Number not Odds Income Working Working of Working 10 2 1 2 / 1 = 2 11 4 1 4 / 1 = 4 12 8 1 8 / 1 = 8
Suppose we compare the odds of working for those earning $10k (2) with those earning $11k (4). If we divide the odds for those earning $11k by the odds for those earning $10k, we get 4 / 2 = 2. Likewise, if we divide the odds of working for those earning $12k by the odds of working for those earning $11k, we get 8 / 4 = 2. Notice that when income increased by 1 unit ($1000) the odds of working increased by a factor of 2. This is what an odds ratio is. In this example, when we increase income by 1 unit, the odds of the wife working increases by a factor of 2.
Another way to compute odds is by using probabilities. For example, families that earn $10k have a probability of .666 of the wife working (1 / 3), and a probability of .333 of the wife NOT working. If we divide the probability of working by the probability of not working, we get the same result as we got before, an odds of 2. This is illustrated in the table below.
Odds Income P(work) P(not work) of Working 10 2/3=.666 1/3=.333 .666 / .333 = 2 11 4/5=.800 1/5=.200 .800 / .200 = 4 12 8/9=.888 1/9=.111 .888 / .111 = 8
Note that we get the same odds whether we used the number working or the prob(working). The second method is the more traditional method, and the one we will use from this point forward.
Understanding coefficients
In addition to looking at odds ratios, you can also look at coefficients. The coefficients are the estimates from the regression equation predicting logits. We get the estimates in the column labeled "B".
logistic regression wifework /method = enter inc.
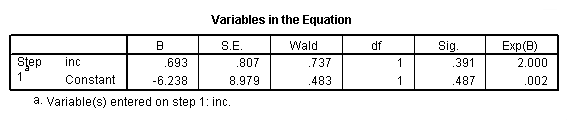
The equation shown obtains the predicted log(odds of wife working) = -6.2383 + inc * .6931 Let’s predict the log(odds of wife working) for income of $10k.
-6.2383 + 10 * .6931 = .6927
We can take the exponential of this to convert the log odds to odds. Taking the exponential of .6927 yields 1.999 or 2. This was the odds we found for a wife working in a family earning $10k.
We can convert the odds to a probability. The formula for converting an odds to probability is probability = odds / (1 + odds). We see the predicted probability of a wife working when the family earns $10k is .666.
2 / (1 + 2) = .66666667
By the way, if we take the exponential of a coefficient, it is the odds ratio.
2. contrived example, odds ratio of 1.1
Below we explore another example, except in this case the odds ratio is 1.1 . Like before, there is a variable called inc that represents the income of the family, and wifework that is 1 if the wife works, 0 if she does not. Below we use the file.
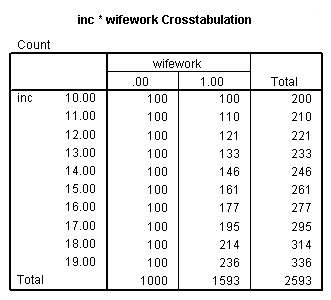
data list list /inc wifework freq. begin data. 10 0 100 10 1 100 11 0 100 11 1 110 12 0 100 12 1 121 13 0 100 13 1 133 14 0 100 14 1 146 15 0 100 15 1 161 16 0 100 16 1 177 17 0 100 17 1 195 18 0 100 18 1 214 19 0 100 19 1 236 end data.
weight by freq.
Below we use the crosstabs command to look at the number of wives who work (and don’t work) for each level of income. For example, there were 233 families earning $13,000, of which 133 had working wives and 100 had non-working wives.
crosstabs inc by wifework.
Let’s perform a logistic regression predicting wifework from inc.
logistic regression wifework /method = enter inc.

This time we get an odds ratio of 1.1. Let’s see how we would interpret this.
-------------------------------------------------------------------------------
Dependent variable: wifework Command: logistic
-------------------------------------------------------------------------------
----------+-----------
inc | exp(xb)
----------+-----------
10 | .999386
11 | 1.09935
12 | 1.20932
13 | 1.33029
14 | 1.46335
15 | 1.60973
16 | 1.77075
17 | 1.94788
18 | 2.14272
19 | 2.35705
----------+-----------
Key: exp(xb) = exp(xb)
We see that the odds of the wife working for inc of 10 is .999 (let’s say 1.0). The odds ratio of 1.1 tells us that the odds of the wife working should go up by a factor of 1.1 for ever unit increase in inc. Let’s see how this works. If the family makes $11,000, the odds of the wife working will be 1.1 times greater or 1.1. If the family makes $12,000 the odds will again be 1.1 times greater or 1.1 * 1.1 or 1.21. If a family makes $13,000 the odds will again be 1.1 times greater or 1.3 * 1.1 = 1.33.
Say that we wanted to know the odds of the wife working if we increased income by an additional 5 units ($5,000) to be $18,000. The odds would go up by 1.15 = 1.61 times. So we would multiple the odds at $13,000 (1.33) by 1.61 = 2.14. So the odds of a wife working if the husband earns $18,000 is predicted to be 1.61, just as shown in the table above.
This shows that you can interpret the odds ratio in a couple of ways.
1. For a one unit change in the predictor, the odds of a wife working increases by the odds ratio.
2. For an x unit change in the predictor, the odds of a wife working increases by the odds ratio to the x power, odds-ratiox.
2. Contrived example with odds ratio of 1.5
Here is another example like the ones above, except that the odds ratio is 1.5.
clear use oddsrat3 , clear
Here we show the number of wives who work, and don’t work at each level of income.
tabulate inc wifework
| wifework
inc | 0 1 | Total
-----------+----------------------+----------
10 | 100 100 | 200
11 | 100 150 | 250
12 | 100 225 | 325
13 | 100 338 | 438
14 | 100 506 | 606
15 | 100 759 | 859
16 | 100 1139 | 1239
17 | 100 1709 | 1809
18 | 100 2563 | 2663
19 | 100 3844 | 3944
-----------+----------------------+----------
Total | 1000 11333 | 12333
Below we perform a logistic regression. We see that the odds ratio is 1.5.
logistic wifework inc
Logit estimates Number of obs = 12333
LR chi2(1) = 1041.24
Prob > chi2 = 0.0000
Log likelihood = -2949.9768 Pseudo R2 = 0.1500
------------------------------------------------------------------------------
wifework | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
inc | 1.499958 .0191732 31.718 0.000 1.462846 1.538012
------------------------------------------------------------------------------
We can use the adjust command with the exp option to get the predicted odds of the wife working at each level of income. We can see that for every unit increase in inc, the odds of the wife working increases by a factor of 1.5. Try taking any of the odds ratios and multiplying it by 1.5 and you will get the odds ratio for the next level of income, e.g. taking the odds for income of 11 is 1.5, and multiplying that by 1.5 gives 2.25, which is the odds of working for an income of 12.
adjust , by(inc) exp
-------------------------------------------------------------------------------
Dependent variable: wifework Command: logistic
-------------------------------------------------------------------------------
----------+-----------
inc | exp(xb)
----------+-----------
10 | 1.00019
11 | 1.50025
12 | 2.25031
13 | 3.37537
14 | 5.06291
15 | 7.59415
16 | 11.3909
17 | 17.0859
18 | 25.6281
19 | 38.4411
----------+-----------
Key: exp(xb) = exp(xb)
3. Contrived example, odds ratio of .66667
All the examples we have looked at so far have had odds ratios that are greater than one. When the odds ratio is over 1, the odds of, say the wife working, increases as the predictor increases. On the other hand, if the odds ratio is less than one, the odds of the wife working decreases as the predictor increases.
clear
use oddsrat4 , clear
tabulate inc wifework
| wifework
inc | 0 1 | Total
-----------+----------------------+----------
10 | 100 3844 | 3944
11 | 100 2563 | 2663
12 | 100 1709 | 1809
13 | 100 1139 | 1239
14 | 100 759 | 859
15 | 100 506 | 606
16 | 100 338 | 438
17 | 100 225 | 325
18 | 100 150 | 250
19 | 100 100 | 200
-----------+----------------------+----------
Total | 1000 11333 | 12333
We indeed see that the odds ratio is .666.
logistic wifework inc
Logit estimates Number of obs = 12333
LR chi2(1) = 1041.24
Prob > chi2 = 0.0000
Log likelihood = -2949.9768 Pseudo R2 = 0.1500
------------------------------------------------------------------------------
wifework | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
inc | .6666852 .0085219 -31.718 0.000 .6501901 .6835989
------------------------------------------------------------------------------
We can get the odds of the wife working using the adjust command. You can see that the odds of the wife working go down as income increases. In fact, the income goes down by a factor of .666.
adjust , by(inc) exp
-------------------------------------------------------------------------------
Dependent variable: wifework Command: logistic
-------------------------------------------------------------------------------
----------+-----------
inc | exp(xb)
----------+-----------
10 | 38.4411
11 | 25.6281
12 | 17.0859
13 | 11.3909
14 | 7.59415
15 | 5.06291
16 | 3.37537
17 | 2.25031
18 | 1.50025
19 | 1.00019
----------+-----------
Key: exp(xb) = exp(xb)
For an income of 10, the odds of the wife working are 38.4411. If we multiply this by the odds ratio of .6666 we get get 25.62, which is the odds of a wife working when the husband earns 11.
When the odds ratio for inc is more than 1, an increase in inc increased the odds of the wife working. When the odds ratio for inc is less than one, an increase in inc leads to a decreased odss of the wife working. If the odds ratio for inc is exactly 1, the odds of the wife working would not change when income changes.
5. Contrived example, 2 groups 1.1, and 1.5
Let us combine the data files from example 2 (where the odds ratio was 1.1) and example 3 (where the odds ratio was 1.5). Also, let’s assume that example 2 was composed of families without children, and example 3 was from families with children. Below we combine the files, making child 0 for the data from example 2 and child 1 for the data from example 3.
use oddsrat2, clear gen child = 0 append using oddsrat3 replace child = 1 if child == . (12333 real changes made)
We know from running the previous logistic regressions that the odds ratio was 1.1 for the group with children, and 1.5 for the families without children. Below we run a logistic regression and see that the odds ratio for inc is between 1.1 and 1.5 at about 1.32.
logistic wifework inc child
Logit estimates Number of obs = 14926
LR chi2(2) = 2187.87
Prob > chi2 = 0.0000
Log likelihood = -4785.5667 Pseudo R2 = 0.1861
------------------------------------------------------------------------------
wifework | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
inc | 1.320337 .0128444 28.565 0.000 1.295401 1.345754
child | 4.624184 .2583505 27.409 0.000 4.144565 5.159305
------------------------------------------------------------------------------
We know that the odds ratio of 1.32 is too high for those without children (who had an odds ratio of 1.1), and too low for those with children (who had an odds ratio of 1.5).
Below we create an interaction term by multiplying inc and child creating incchild.
generate incchild = inc*child
We now include incchild as a term in the regression.
logistic wifework inc child incchild
Logit estimates Number of obs = 14926
LR chi2(3) = 2446.43
Prob > chi2 = 0.0000
Log likelihood = -4656.2835 Pseudo R2 = 0.2080
------------------------------------------------------------------------------
wifework | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
inc | 1.100029 .0156951 6.682 0.000 1.069693 1.131225
child | .0450401 .0130882 -10.669 0.000 .0254828 .0796069
incchild | 1.363563 .0261209 16.188 0.000 1.313316 1.415732
------------------------------------------------------------------------------
The odds ratio for inc of 1.1 is the same as the odds ratio for the group without children (when children=0). This tells us that for families with no children, every unit increase in income increases the odds of the wife working increases by a factor of 1.1.
The odds ratio for the term incchild is 1.36, which tells us that for families with children, for every unit increase in income the odds of the wife working increases by an additional factor of 1.36. So, for families with children, for a unit increase in income, the odds of the wife working increases by 1.1 times 1.36 which is 1.5 (1.496 rounds to 1.5). This is as we saw above, that for families with children, the odds ratio was 1.5.
We can confirm the odds ratio by looking at the odds of women working separately for those with children, and without children. Let’s use the prediction formula to confirm the results described above. We can compare the odds of the wife working for those earning $12,000 and $13,000 for those without children.
display exp( _b[_cons] + 12*_b[inc] + 0*_b[child] + 0 * _b[incchild] )
1.2093207
display exp( _b[_cons] + 13*_b[inc] + 0*_b[child] + 0 * _b[incchild] )
1.3302875
We see that this odds ratio is 1.1, as we expected.
display 1.33 / 1.21
1.0991736
Likewise, let’s use the equation to make the predictions for those with children, comparing those earning $12,000 and those earning $13,000.
display exp( _b[_cons] + 12*_b[inc] + 1*_b[child] + 12 * _b[incchild] )
2.2503079
display exp( _b[_cons] + 13*_b[inc] + 1*_b[child] + 13 * _b[incchild] )
3.3753679
We see that this odds ratio is 1.5, as we expected.
display 3.375 / 2.25
1.5
Concluding comments
In these examples, we have tried to help make it easier to understand an interpret odds ratios. We have fabricated data with certain odds ratios making data that fits perfectly. If this were linear OLS regression, it would be like making up X and Y data and making up data that fits a line perfectly. When you analyze your data, it will not fit perfectly so you won’t see the kind of perfect relationships we have shown. But, when you analyze your data the predicted values will be like the examples we have explored. The difference is that in the examples we considered here, the data fit the predicted values exactly. In your data, there will be discrepancies between the predicted and actual values.
