This page shows an example of a canonical correlation analysis with footnotes explaining the output in SPSS. A researcher has collected data on three psychological variables, four academic variables (standardized test scores) and gender for 600 college freshman. She is interested in how the set of psychological variables relates to the academic variables and gender. In particular, the researcher is interested in how many dimensions are necessary to understand the association between the two sets of variables.
We have a data file, https://stats.idre.ucla.edu/wp-content/uploads/2016/02/mmr.sav, with 600 observations on eight variables. The psychological variables are locus of control, self-concept and motivation. The academic variables are standardized test scores in reading, writing, math and science. Additionally, the variable female is a zero-one indicator variable with the one indicating a female student. The researcher is interested in the relationship between the psychological variables and the academic variables, with gender considered as well. Canonical correlation analysis aims to find pairs of linear combinations of each group of variables that are highly correlated. These linear combinations are called canonical variates. Each canonical variate is orthogonal to the other canonical variates except for the one with which its correlation has been maximized. The possible number of such pairs is limited to the number of variables in the smallest group. In our example, there are three psychological variables and more than three academic variables. Thus, a canonical correlation analysis on these sets of variables will generate three pairs of canonical variates.
To begin, let’s read in and summarize the dataset.
get file='d:\data\mmr.sav'. descriptives variables=locus_of_control self_concept motivation read write math science female /statistics=mean stddev min max.
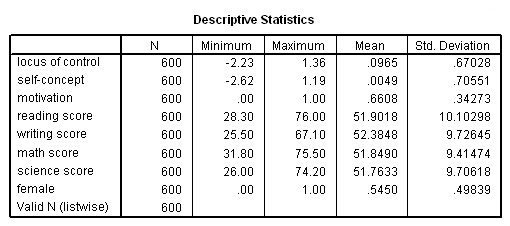
These descriptives indicate that there are not any missing values in the data and suggest the different scales the different variables. We can proceed with the canonical correlation analysis without worries of missing data, keeping in mind that our variables differ widely in scale.
SPSS performs canonical correlation using the manova command with the discrim option. The manova command is one of the SPSS commands that can only be accessed via syntax; there is not a sequence of pull-down menus or point-and-clicks that could arrive at this analysis.
Due to the length of the output, we will be omitting some of the output that is extraneous to our canonical correlation analysis and making comments in several places along the way.
In the manova command, we first list the variables in our psychological group (locus_of_control, self_concept and motivation). Then, after the SPSS keyword with, we list the variables in our academic group (read, write, math, science and female). SPSS refers to the first group of variables as the “dependent variables” and the second group of variables as the “covariates”. This follows manova convention.
manova locus_of_control self_concept motivation with read write math science female / discrim all alpha(1) / print=sig(eigen dim).
...[additional output omitted]...
* * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * *
EFFECT .. WITHIN CELLS Regression
Multivariate Tests of Significance (S = 3, M = 1/2, N = 295 )
Test Name Value Approx. F Hypoth. DF Error DF Sig. of F
Pillais .25425 11.00057 15.00 1782.00 .000
Hotellings .31430 12.37633 15.00 1772.00 .000
Wilks .75436 11.71573 15.00 1634.65 .000
Roys .21538
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Eigenvalues and Canonical Correlations
Root No. Eigenvalue Pct. Cum. Pct. Canon Cor. Sq. Cor
1 .274 87.336 87.336 .464 .215
2 .029 9.185 96.522 .168 .028
3 .011 3.478 100.000 .104 .011
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Dimension Reduction Analysis
Roots Wilks L. F Hypoth. DF Error DF Sig. of F
1 TO 3 .75436 11.71573 15.00 1634.65 .000
2 TO 3 .96143 2.94446 8.00 1186.00 .003
3 TO 3 .98919 2.16461 3.00 594.00 .091
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
...[additional output omitted]...
* * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * *
Raw canonical coefficients for DEPENDENT variables
Function No.
Variable 1 2 3
locus_of 1.254 -.621 .662
self_con -.351 -1.188 -.827
motivati 1.262 2.027 -2.000
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Standardized canonical coefficients for DEPENDENT variables
Function No.
Variable 1 2 3
locus_of .840 -.417 .444
self_con -.248 -.838 -.583
motivati .433 .695 -.686
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Correlations between DEPENDENT and canonical variables
Function No.
Variable 1 2 3
locus_of .904 -.390 .176
self_con .021 -.709 -.705
motivati .567 .351 -.745
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Variance in dependent variables explained by canonical variables
CAN. VAR. Pct Var DE Cum Pct DE Pct Var CO Cum Pct CO
1 37.980 37.980 8.180 8.180
2 25.910 63.889 .727 8.907
3 36.111 100.000 .391 9.297
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Raw canonical coefficients for COVARIATES
Function No.
COVARIATE 1 2 3
read .045 -.005 -.021
write .036 .042 -.091
math .023 .004 -.009
science .005 -.085 .110
female .632 1.085 1.795
* * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * *
Standardized canonical coefficients for COVARIATES
CAN. VAR.
COVARIATE 1 2 3
read .451 -.050 -.216
write .349 .409 -.888
math .220 .040 -.088
science .049 -.827 1.066
female .315 .541 .894
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Correlations between COVARIATES and canonical variables
CAN. VAR.
Covariate 1 2 3
read .840 -.359 -.135
write .877 .065 -.255
math .764 -.298 -.148
science .658 -.677 .230
female .364 .755 .543
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Variance in covariates explained by canonical variables
CAN. VAR. Pct Var DE Cum Pct DE Pct Var CO Cum Pct CO
1 11.305 11.305 52.488 52.488
2 .701 12.006 24.994 77.482
3 .098 12.104 9.066 86.548
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
...[additional output omitted]...
Data Summary, Eigenvalues and Hypothesis Tests
* * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * * EFFECT .. WITHIN CELLS Regression Multivariate Tests of Significance (S = 3, M = 1/2, N = 295 ) Test Name Valuee Approx. Ff Hypoth. DFg Error DFg Sig. of Fh Pillaisa .25425 11.00057 15.00 1782.00 .000 Hotellingsb .31430 12.37633 15.00 1772.00 .000 Wilksc .75436 11.71573 15.00 1634.65 .000 Roysd .21538 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Eigenvalues and Canonical Correlations Root No.i Eigenvaluej Pct.k Cum. Pct.l Canon Cor.m Sq. Corn 1 .274 87.336 87.336 .464 .215 2 .029 9.185 96.522 .168 .028 3 .011 3.478 100.000 .104 .011 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Dimension Reduction Analysis Rootso Wilks L.p Ff Hypoth. DFg Error DFg Sig. of Fh 1 TO 3 .75436 11.71573 15.00 1634.65 .000 2 TO 3 .96143 2.94446 8.00 1186.00 .003 3 TO 3 .98919 2.16461 3.00 594.00 .091
a. Pillais – This is Pillai’s trace, one of the four multivariate statistics calculated by SPSS to test the null hypothesis that the canonical correlations are zero (which, in turn, means that there is no linear relationship between the two specified groups of variables). Pillai’s trace is the sum of the squared canonical correlations, which can be found in the next section of output (see superscript n): 0.4642 + 0.1682 + 0.1042 = 0.25425.
b. Hotellings – This is the Hotelling-Lawley trace. It is very similar to Pillai’s trace and can be calculated as the sum of the values of (canonical correlation2/(1-canonical correlation2)). We can calculate 0.4642 /(1- 0.4642) + 0.1682/(1-0.1682) + 0.1042/(1-0.1042) = 0.31430.
c. Wilks – This is Wilks’ lambda, another multivariate statistic calculated by SPSS. It is the product of the values of (1-canonical correlation2). In this example, our canonical correlations are 0.4641, 0.1675, and 0.1040 so the Wilks’ Lambda is (1- 0.4642)*(1-0.1682)*(1-0.1042) = 0.75436.
d. Roys – This is Roy’s greatest root. It can be calculated from the largest eigenvalue: largest eigenvalue/(1 + largest eigenvalue). Because it is based on a maximum, it can behave differently from the other three test statistics. In instances where the other three are not statistically significant and Roy’s is statistically significant, the effect should be considered to be not statistically significant.
e. Value – This is the value of the multivariate test listed in the prior column.
f. (Approx.) F – These are the F values associated with the various tests that are included in SPSS’s output. For the multivariate tests, the F values are approximate.
g. Hypoth. DF, Error DF – These are the degrees of freedom used in determining the F values. Note that there are instances in which the degrees of freedom may be a non-integer because these degrees of freedom are calculated using the mean squared errors, which are often non-integers.
h. Sig. of F – This is the p-value associated with the F value of a given test statistic. The null hypothesis that our two sets of variables are not linearly related is evaluated with regard to this p-value. For a given alpha level, such as 0.05, if the p-value is less than alpha, the null hypothesis is rejected. If not, then we fail to reject the null hypothesis.
i. Root No. – This is the rank of the given eigenvalue (largest to smallest). There are as many roots as there were variables in the smaller of the two variable sets. In this example, our set of psychological variables contains three variables and our set of academic variables contains five variables. Thus the smaller variable set contains three variables and the analysis generates three roots.
j. Eigenvalue – These are the eigenvalues of the product of the model matrix and the inverse of the error matrix. These eigenvalues can also be calculated using the squared canonical correlations. The largest eigenvalue is equal to largest squared correlation /(1- largest squared correlation); 0.215/(1-0.215) = 0.274. These calculations can be completed for each correlation to find the corresponding eigenvalue. The relative size of the eigenvalues reflect how much of the variance in the canonical variates can be explained by the corresponding canonical correlation. Thus, the eigenvalue corresponding to the first correlation is greatest, and all subsequent eigenvalues are smaller.
k. Pct. – This is the percent of the sum of the eigenvalues represented by a given eigenvalue. The sum of the three eigenvalues is (0.2745+0.0289+0.0109) = 0.3143. Then, the proportions can be calculated: 0.2745/0.3143 = 0.8734, 0.0289/0.3143 = 0.0919, and 0.0109/0.3143 = 0.0348. This is the proportion of explained variance in the canonical variates attributed to a given canonical correlation.
l. Cum. Pct. – This is the cumulative sum of the percents.
m. Canon Cor. – These are the Pearson correlations of the pairs of canonical variates. The first pair of variates, a linear combination of the psychological measurements and a linear combination of the academic measurements, has a correlation coefficient of 0.464. The second pair has a correlation coefficient of 0.168, and the third pair 0.104. Each subsequent pair of canonical variates is less correlated. These can be interpreted as any other Pearson correlations. That is, the square of the correlation represents the proportion of the variance in one group’s variate explained by the other group’s variate.
n. Sq. Cor – These are the squares of the canonical correlations. For example, (0.464*0.464) = 0.215.
o. Roots – This is the set of roots included in the null hypothesis being tested. The null hypothesis is that all of the correlations associated with the roots in the given set are equal to zero in the population. By testing these different sets of roots, we are determining how many dimensions are required to describe the relationship between the two groups of variables. Because each root is less informative than the one before it, unnecessary dimensions will be associated with the smallest eigenvalues. Thus, we start our test with the full set of roots and then test subsets generated by omitting the greatest root in the previous set. Here, we first tested all three roots, then roots two and three, and then root three alone.
p. Wilks L. – Here, the Wilks lambda test statistic is used for testing the null hypothesis that the given canonical correlation and all smaller ones are equal to zero in the population. Each value can be calculated as the product of the values of (1-canonical correlation2) for the set of canonical correlations being tested. In this example, our canonical correlations are 0.464, 0.168 and 0.104, so the value for testing that all three of the correlations are zero is (1- 0.4642)*(1-0.1682)*(1-0.1042) = 0.75436. To test that the two smaller canonical correlations, 0.168 and 0.104, are zero in the population, the value is (1-0.1682)*(1-0.1042) = 0.96143. The value for testing that the smallest canonical correlation is zero is (1-0.1042) = 0.98919.
Canonical Coefficients, Correlations, and Variance Explained
* * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * * Raw canonical coefficients for DEPENDENT variablesq Function No. Variable 1 2 3 locus_of 1.254 -.621 .662 self_con -.351 -1.188 -.827 motivati 1.262 2.027 -2.000 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Standardized canonical coefficients for DEPENDENT variablesr Function No. Variable 1 2 3 locus_of .840 -.417 .444 self_con -.248 -.838 -.583 motivati .433 .695 -.686 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Correlations between DEPENDENT and canonical variabless Function No. Variable 1 2 3 locus_of .904 -.390 .176 self_con .021 -.709 -.705 motivati .567 .351 -.745 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Variance in dependent variables explained by canonical variablest CAN. VAR. Pct Var DE Cum Pct DE Pct Var CO Cum Pct CO 1 37.980 37.980 8.180 8.180 2 25.910 63.889 .727 8.907 3 36.111 100.000 .391 9.297 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Raw canonical coefficients for COVARIATESq Function No. COVARIATE 1 2 3 read .045 -.005 -.021 write .036 .042 -.091 math .023 .004 -.009 science .005 -.085 .110 female .632 1.085 1.795 * * * * * * A n a l y s i s o f V a r i a n c e -- design 1 * * * * * * Standardized canonical coefficients for COVARIATESr CAN. VAR. COVARIATE 1 2 3 read .451 -.050 -.216 write .349 .409 -.888 math .220 .040 -.088 science .049 -.827 1.066 female .315 .541 .894 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Correlations between COVARIATES and canonical variabless CAN. VAR. Covariate 1 2 3 read .840 -.359 -.135 write .877 .065 -.255 math .764 -.298 -.148 science .658 -.677 .230 female .364 .755 .543 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - Variance in covariates explained by canonical variablesu CAN. VAR. Pct Var DE Cum Pct DE Pct Var CO Cum Pct CO 1 11.305 11.305 52.488 52.488 2 .701 12.006 24.994 77.482 3 .098 12.104 9.066 86.548 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
q. Raw canonical coefficients for DEPENDENT/COVARIATE variables – These are the raw canonical coefficients. They define the linear relationship between the variables in a given group and the canonical variates. They can be interpreted in the same manner as regression coefficients, assuming the canonical variate as the outcome variable. For example, a one unit increase in locus_of_control leads to a 1.254 unit increase in the first variate of the psychological measurements, and a one unit increase in read score leads to a 0.045 unit increase in the first variate of the academic measurements. Recall that our variables varied in scale. This is reflected in the varied scale of these raw coefficients.
r. Standardized canonical coefficients for DEPENDENT/COVARIATE variables – These are the standardized canonical coefficients. This means that, if all of the variables in the analysis are rescaled to have a mean of zero and a standard deviation of 1, the coefficients generating the canonical variates would indicate how a one standard deviation increase in the variable would change the variate. For example, an increase of one standard deviation in locus_of_control would lead to a 0.840 standard deviation increase in the first variate of the psychological measurements, and an increase of one standard deviation in read would lead to a 0.451 standard deviation increase in the first variate of the academic measurements.
s. Correlations between DEPENDENT/COVARIATE variables and canonical variables – These are the correlations between each variable in a group and the group’s canonical variates. For example, we can see in the “dependent” variables that locus_of_control has a Pearson correlation of 0.904 with the first psychological variate, -0.390 with the second psychological variate, and 0.176 with the third psychological variate. In the “covariates” section, we can see that read has a Pearson correlation of 0.840 with the first academic variate, -0.359 with the second academic variate, and -0.135 with the third academic variate.
t. Variance in dependent variables explained by canonical variables – This is the degree to which the canonical variates of both the dependent variables (DE) and covariates (CO) can explain the standardized variability in the dependent variables. For both sets of canonical variates, the percent and cumulative percent of variability explained by each variate is displayed.
u. Variance in covariates explained by canonical variables – This is the degree to which the canonical variates of both the dependent variables (DE) and covariates (CO) can explain the standardized variability in the covariates. For both sets of canonical variates, the percent and cumulative percent of variability explained by each variate is displayed.
For further information on canonical correlation analysis in SPSS, see the corresponding Data Analysis Example page.
