The t-test procedure performs t-tests for one sample, two samples and paired observations. The single-sample t-test compares the mean of the sample to a given number (which you supply). The independent samples t-test compares the difference in the means from the two groups to a given value (usually 0). In other words, it tests whether the difference in the means is 0. The dependent-sample or paired t-test compares the difference in the means from the two variables measured on the same set of subjects to a given number (usually 0), while taking into account the fact that the scores are not independent. In our examples, we will use the hsb2 data set.
Single sample t-test
The single sample t-test tests the null hypothesis that the population mean is equal to the number specified by the user. SPSS calculates the t-statistic and its p-value under the assumption that the sample comes from an approximately normal distribution. If the p-value associated with the t-test is small (0.05 is often used as the threshold), there is evidence that the mean is different from the hypothesized value. If the p-value associated with the t-test is not small (p > 0.05), then the null hypothesis is not rejected and you can conclude that the mean is not different from the hypothesized value.
In this example, the t-statistic is 4.140 with 199 degrees of freedom. The corresponding two-tailed p-value is .000, which is less than 0.05. We conclude that the mean of variable write is different from 50.
get file "C:\data\hsb2.sav".
t-test /testval=50 variables=write.
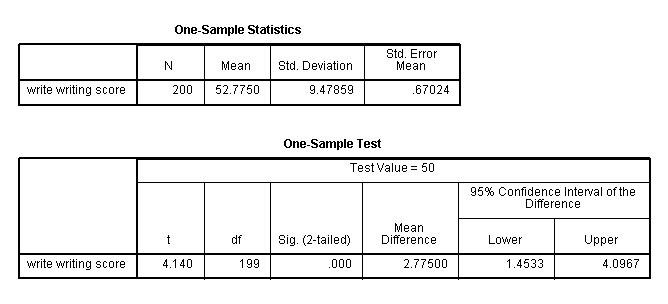
One-Sample Statistics
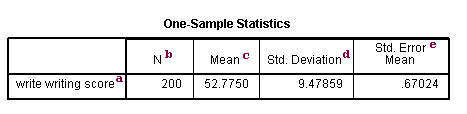
a. – This is the list of variables. Each variable that was listed on the variables= statement in the above code will have its own line in this part of the output.
b. N – This is the number of valid (i.e., non-missing) observations used in calculating the t-test.
c. Mean – This is the mean of the variable.
d. Std. Deviation – This is the standard deviation of the variable.
e. Std. Error Mean – This is the estimated standard deviation of the sample mean. If we drew repeated samples of size 200, we would expect the standard deviation of the sample means to be close to the standard error. The standard deviation of the distribution of sample mean is estimated as the standard deviation of the sample divided by the square root of sample size: 9.47859/(sqrt(200)) = .67024.
Test statistics
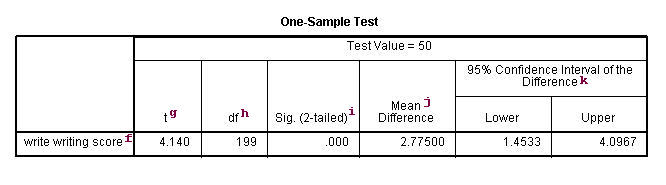
f. – This identifies the variables. Each variable that was listed on the variables= statement will have its own line in this part of the output. If a variables= statement is not specified, t-test will conduct a t-test on all numerical variables in the dataset.
g. t – This is the Student t-statistic. It is the ratio of the difference between the sample mean and the given number to the standard error of the mean: (52.775 – 50) / .6702372 = 4.1403. Since the standard error of the mean measures the variability of the sample mean, the smaller the standard error of the mean, the more likely that our sample mean is close to the true population mean. This is illustrated by the following three figures.
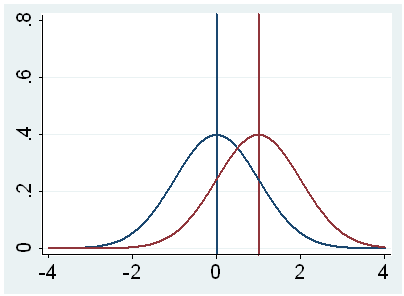
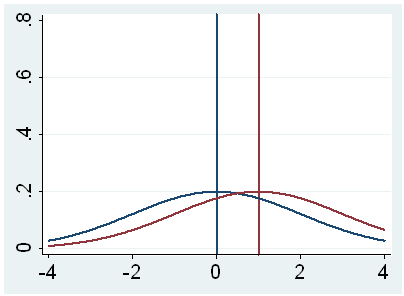
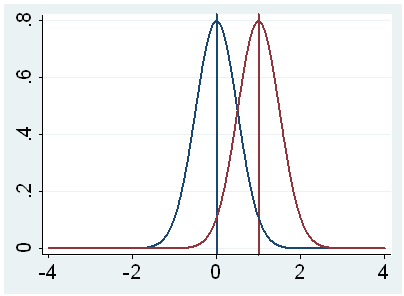
In all three cases, the difference between the population means is the same. But with large variability of sample means, second graph, two populations overlap a great deal. Therefore, the difference may well come by chance. On the other hand, with small variability, the difference is more clear as in the third graph. The smaller the standard error of the mean, the larger the magnitude of the t-value and therefore, the smaller the p-value.
h. df – The degrees of freedom for the single sample t-test is simply the number of valid observations minus 1. We lose one degree of freedom because we have estimated the mean from the sample. We have used some of the information from the data to estimate the mean, therefore it is not available to use for the test and the degrees of freedom accounts for this.
i. Sig (2-tailed)– This is the two-tailed p-value evaluating the null against an alternative that the mean is not equal to 50. It is equal to the probability of observing a greater absolute value of t under the null hypothesis. If the p-value is less than the pre-specified alpha level (usually .05 or .01) we will conclude that mean is statistically significantly different from zero. For example, the p-value is smaller than 0.05. So we conclude that the mean for write is different from 50.
j. Mean Difference – This is the difference between the sample mean and the test value.
k. 95% Confidence Interval of the Difference – These are the lower and upper bound of the confidence interval for the mean. A confidence interval for the mean specifies a range of values within which the unknown population parameter, in this case the mean, may lie. It is given by
![]()
where s is the sample deviation of the observations and N is the number of valid observations. The t-value in the formula can be computed or found in any statistics book with the degrees of freedom being N-1 and the p-value being 1-alpha/2, where alpha is the confidence level and by default is .95.
Paired t-test
A paired (or “dependent”) t-test is used when the observations are not independent of one another. In the example below, the same students took both the writing and the reading test. Hence, you would expect there to be a relationship between the scores provided by each student. The paired t-test accounts for this. For each student, we are essentially looking at the differences in the values of the two variables and testing if the mean of these differences is equal to zero.
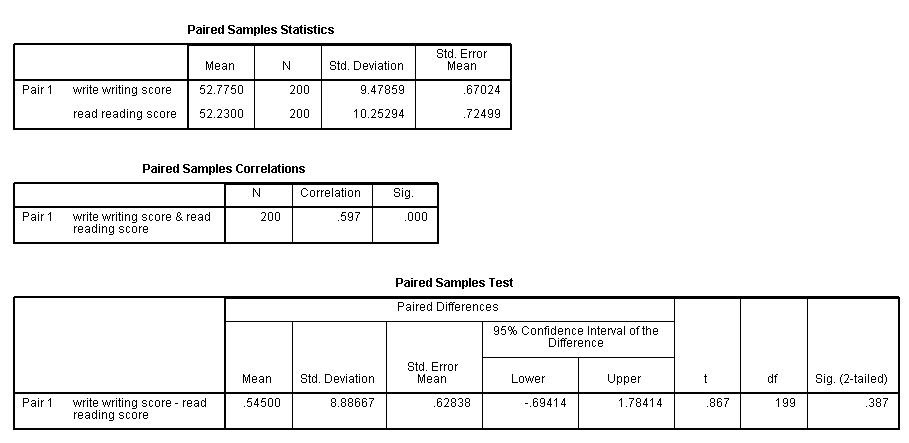
In this example, the t-statistic is 0.8673 with 199 degrees of freedom. The corresponding two-tailed p-value is 0.3868, which is greater than 0.05. We conclude that the mean difference of write and read is not different from 0.
t-test pairs=write with read (paired).
Summary statistics
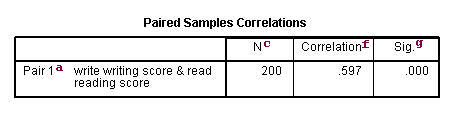
a. – This is the list of variables.
b. Mean – These are the respective means of the variables.
c. N – This is the number of valid (i.e., non-missing) observations used in calculating the t-test.
d. Std. Deviation – This is the standard deviations of the variables.
e. Std Error Mean – Standard Error Mean is the estimated standard deviation of the sample mean. This value is estimated as the standard deviation of one sample divided by the square root of sample size: 9.47859/sqrt(200) = .67024, 10.25294/sqrt(200) = .72499. This provides a measure of the variability of the sample mean.
f. Correlation – This is the correlation coefficient of the pair of variables indicated. This is a measure of the strength and direction of the linear relationship between the two variables. The correlation coefficient can range from -1 to +1, with -1 indicating a perfect negative correlation, +1 indicating a perfect positive correlation, and 0 indicating no correlation at all. (A variable correlated with itself will always have a correlation coefficient of 1.) You can think of the correlation coefficient as telling you the extent to which you can guess the value of one variable given a value of the other variable. The .597 is the numerical description of how tightly around the imaginary line the points lie. If the correlation was higher, the points would tend to be closer to the line; if it was smaller, they would tend to be further away from the line.
g. Sig – This is the p-value associated with the correlation. Here, correlation is significant at the .05 level.
Test statistics
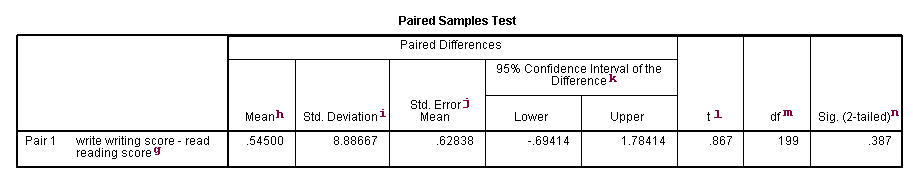
g. writing score-reading score – This is the value measured within each subject: the difference between the writing and reading scores. The paired t-test forms a single random sample of the paired difference. The mean of these values among all subjects is compared to 0 in a paired t-test.
h. Mean – This is the mean within-subject difference between the two variables.
i. Std. Deviation – This is the standard deviation of the mean paired difference.
j. Std Error Mean – This is the estimated standard deviation of the sample mean. This value is estimated as the standard deviation of one sample divided by the square root of sample size: 8.88667/sqrt(200) = .62838. This provides a measure of the variability of the sample mean.
k. 95% Confidence Interval of the Difference – These are the lower and upper bound of the confidence interval for the mean difference. A confidence interval for the mean specifies a range of values within which the unknown population parameter, in this case the mean, may lie. It is given by
![]()
where s is the sample deviation of the observations and N is the number of valid observations. The t-value in the formula can be computed or found in any statistics book with the degrees of freedom being N-1 and the p-value being 1-alpha/2, where alpha is the confidence level and by default is .95.
l. t – This is the t-statistic. It is the ratio of the mean of the difference to the standard error of the difference: (.545/.62838).
m. degrees of freedom – The degrees of freedom for the paired observations is simply the number of observations minus 1. This is because the test is conducted on the one sample of the paired differences.
n. Sig. (2-tailed) – This is the two-tailed p-value computed using the t distribution. It is the probability of observing a greater absolute value of t under the null hypothesis. If the p-value is less than the pre-specified alpha level (usually .05 or .01, here the former) we will conclude that mean difference between writing score and reading score is statistically significantly different from zero. For example, the p-value for the difference between the two variables is greater than 0.05 so we conclude that the mean difference is not statistically significantly different from 0.
Independent group t-test
This t-test is designed to compare means of same variable between two groups. In our example, we compare the mean writing score between the group of female students and the group of male students. Ideally, these subjects are randomly selected from a larger population of subjects. The test assumes that variances for the two populations are the same. The interpretation for p-value is the same as in other type of t-tests.
In this example, the t-statistic is -3.7341 with 198 degrees of freedom. The corresponding two-tailed p-value is 0.0002, which is less than 0.05. We conclude that the difference of means in write between males and females is different from 0.
t-test groups=female(0 1) /variables=write.
Summary statistics
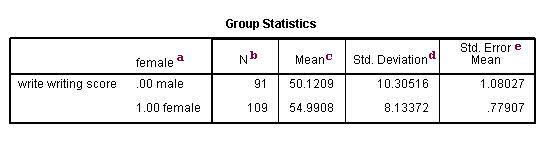
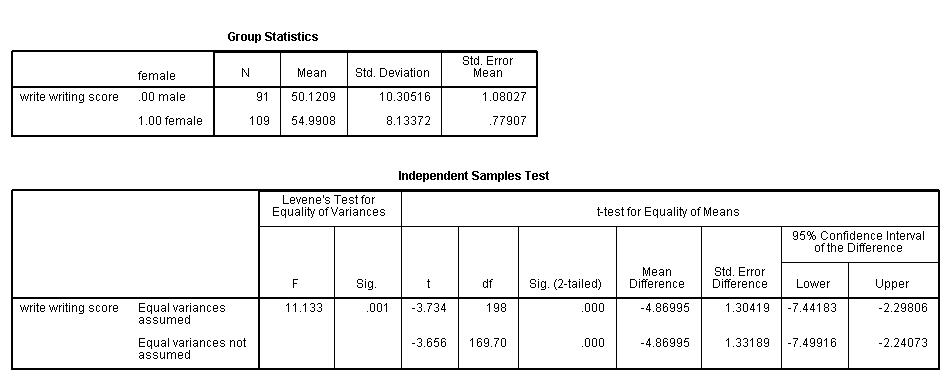
a. female – This column gives categories of the independent variable female. This variable is necessary for doing the independent group t-test and is specified by the t-test groups= statement.
b. N – This is the number of valid (i.e., non-missing) observations in each group.
c. Mean – This is the mean of the dependent variable for each level of the independent variable.
d. Std. Deviation – This is the standard deviation of the dependent variable for each of the levels of the independent variable.
e. Std. Error Mean – This is the standard error of the mean, the ratio of the standard deviation to the square root of the respective number of observations.
Test statistics
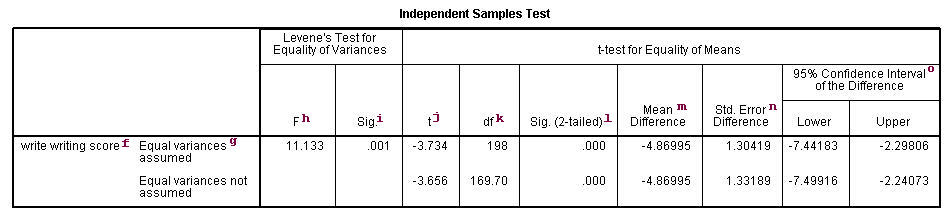
f. – This column lists the dependent variable(s). In our example, the dependent variable is write (labeled “writing score”).
g. – This column specifies the method for computing the standard error of the difference of the means. The method of computing this value is based on the assumption regarding the variances of the two groups. If we assume that the two populations have the same variance, then the first method, called pooled variance estimator, is used. Otherwise, when the variances are not assumed to be equal, the Satterthwaite’s method is used.
h. F– This column lists Levene’s test statistic. Assume \(k\) is the number of groups, \(N\) is the total number of observations, and \(N_i\) is the number of observations in each \(i\)-th group for dependent variable \(Y_{ij}\). Then Levene’s test statistic is defined as
\begin{equation} W = \frac{(N-k)}{(k-1)} \frac{\sum_{i=1}^{k} N_i (\bar{Z}_{i.}-\bar{Z}_{..})^2}{\sum_{i=1}^{k}\sum_{j=1}^{N_i}(Z_{ij}-\bar{Z}_{i.})^2} \end{equation}
\begin{equation} Z_{ij} = |Y_{ij}-\bar{Y}_{i.}| \end{equation}
where \(\bar{Y}_{i.}\) is the mean of the dependent variable and \(\bar{Z}_{i.}\) is the mean of \(Z_{ij}\) for each \(i\)-th group respectively, and \(\bar{Z}_{..}\) is the grand mean of \(Z_{ij}\).
i. Sig. – This is the two-tailed p-value associated with the null that the two groups have the same variance. In our example, the probability is less than 0.05. So there is evidence that the variances for the two groups, female students and male students, are different. Therefore, we may want to use the second method (Satterthwaite variance estimator) for our t-test.
j. t – These are the t-statistics under the two different assumptions: equal variances and unequal variances. These are the ratios of the mean of the differences to the standard errors of the difference under the two different assumptions: (-4.86995 / 1.30419) = -3.734, (-4.86995/1.33189) = -3.656.
k. df – The degrees of freedom when we assume equal variances is simply the sum of the two sample sizes (109 and 91) minus 2. The degrees of freedom when we assume unequal variances is calculated using the Satterthwaite formula.
l. Sig. (2-tailed) – The p-value is the two-tailed probability computed using the t distribution. It is the probability of observing a t-value of equal or greater absolute value under the null hypothesis. For a one-tailed test, halve this probability. If the p-value is less than our pre-specified alpha level, usually 0.05, we will conclude that the difference is significantly different from zero. For example, the p-value for the difference between females and males is less than 0.05 in both cases, so we conclude that the difference in means is statistically significantly different from 0.
m. Mean Difference – This is the difference between the means.
n. Std Error Difference – Standard Error difference is the estimated standard deviation of the difference between the sample means. If we drew repeated samples of size 200, we would expect the standard deviation of the sample means to be close to the standard error. This provides a measure of the variability of the sample mean. The Central Limit Theorem tells us that the sample means are approximately normally distributed when the sample size is 30 or greater. Note that the standard error difference is calculated differently under the two different assumptions.
o. 95% Confidence Interval of the Difference – These are the lower and upper bound of the confidence interval for the mean difference. A confidence interval for the mean specifies a range of values within which the unknown population parameter, in this case the mean, may lie. It is given by
![]()
where s is the sample deviation of the observations and N is the number of valid observations. The t-value in the formula can be computed or found in any statistics book with the degrees of freedom being N-1 and the p-value being 1-width/2, where width is the confidence level and by default is .95.
