The syntax file for this seminar.
There are a number of situations that can arise when the analysis includes between groups effects as well as within subject effects. We start by showing 4 example analyses using measurements of depression over 3 time points broken down by 2 treatment groups. In the first example we see that the two groups differ in depression but neither group changes over time. In the second example the two groups grow in depression but at the same rate over time. In the third example, the two groups start off being quite different in depression but over time the groups get closer in their level of depression. The fourth example shows the groups starting off at the same level of depression, and one group group increases over time whereas the other group decreases over time.
Note that in the interest of making learning the concepts easier we have taken the liberty of using only a very small portion of the voluminous output that SPSS provides and we have inserted the graphs in the beginning of the output rather than at the end.
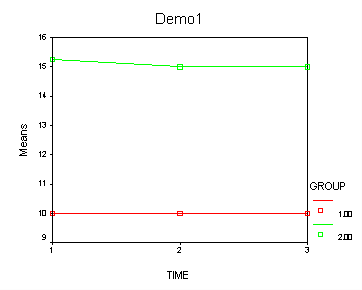
Demo Analysis #1
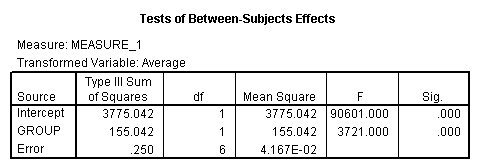
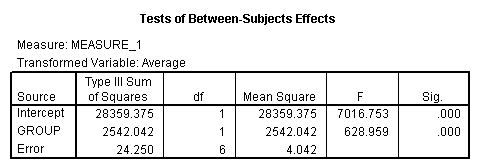
The between groups test indicates that there the variable group is significant, consequently in the graph we see that the lines for the two groups are rather far apart. The within subject test indicate that there is not a significant time effect, in other words, the groups do not change in depression over time. In the graph we see that the groups have lines that are flat, i.e. the slopes of the lines are approximately equal to zero. Also, since the lines are parallel, we are not surprised that there is no interaction.
<Abbreviated output from GLM command>
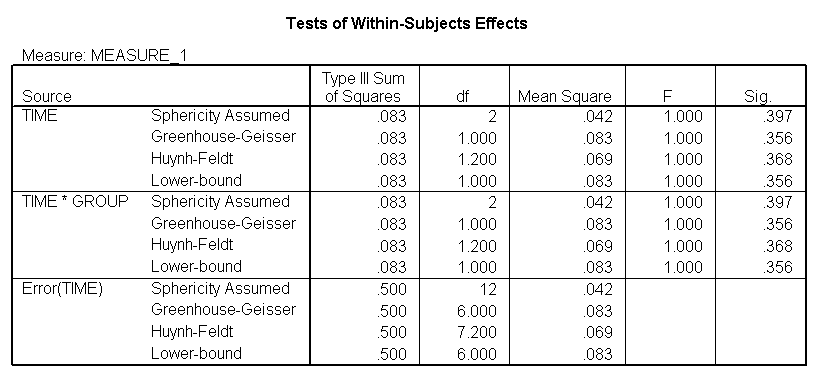
Demo Analysis #2
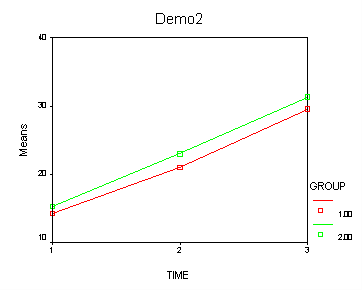
The between groups test indicates that there the variable group is not significant, consequently in the graph we see that the lines for the two groups are rather close together. The within subject test indicate that there is a significant time effect, in other words, the groups do change in depression over time. In the graph we see that the groups have lines that increase over time. Again, the lines are parallel consistent with the finding that the interaction is not significant.
<Abbreviated output from GLM command>
Demo Analysis #3
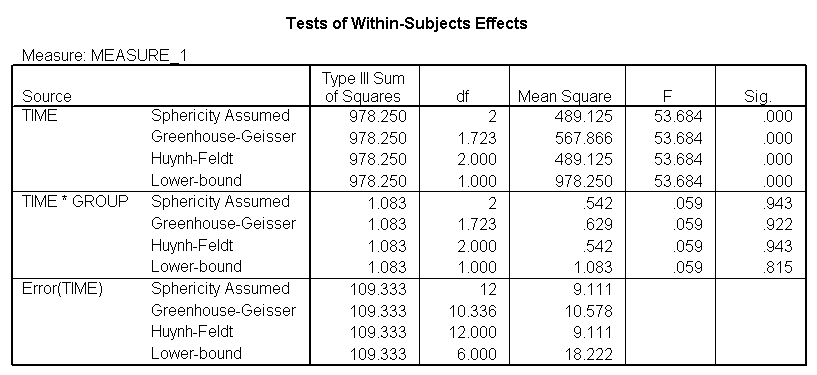
The between groups test indicates that there the variable group is significant, consequently in the graph we see that the lines for the two groups are rather far apart. The within subject test indicate that there is a significant time effect, in other words, the groups do change over time, both groups are getting less depressed over time. Moreover, the interaction of time and group is significant which means that the groups are changing over time but are changing in different ways, which means that in the graph the lines will not be parallel. In the graph we see that the groups have non-parallel lines that decrease over time and are getting progressively closer together over time.
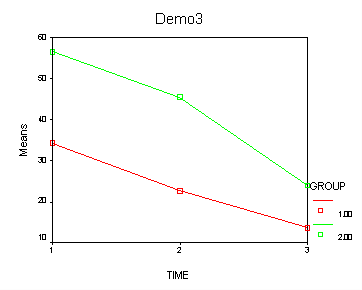
<Abbreviated output from GLM command>
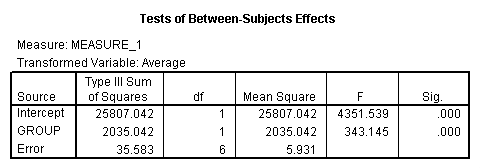
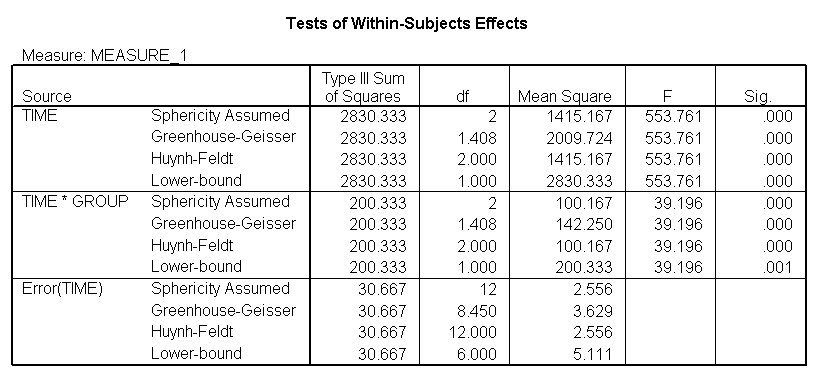
Demo Analysis #4
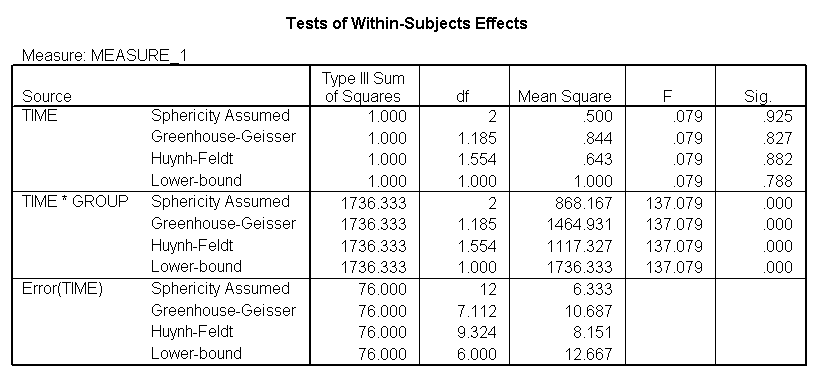
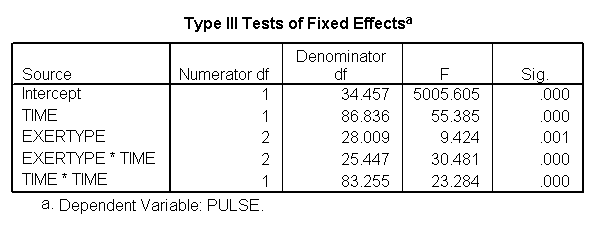
The within subject test indicate that the interaction of time and group is significant. The main effect of time is not significant. However, the significant interaction indicates that the groups are changing over time and they are changing in different ways, in other words, in the graph the lines of the groups will not be parallel. The between groups test indicates that there the variable group is significant. In the graph for this particular case we see that one group is increasing in depression over time and the other group is decreasing in depression over time.
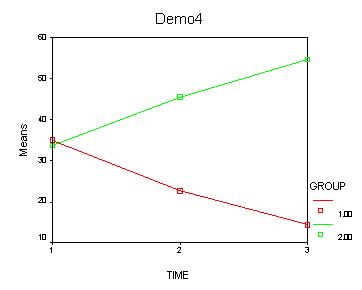
<Abbreviated output from GLM command>
Exercise data examples
The data consists of people who were randomly assigned to two different diets: low-fat and not low-fat and three different types of exercise: at rest, walking leisurely and running. Their pulse rate was measured at three different time points during their assigned exercise: at 1 minute, 15 minutes and 30 minutes.
data list free / id exertype diet time1 time2 time3. begin data. 1 1 1 85 85 88 2 1 1 90 92 93 3 1 1 97 97 94 4 1 1 80 82 83 5 1 1 91 92 91 6 1 2 83 83 84 7 1 2 87 88 90 8 1 2 92 94 95 9 1 2 97 99 96 10 1 2 100 97 100 11 2 1 86 86 84 12 2 1 93 103 104 13 2 1 90 92 93 14 2 1 95 96 100 15 2 1 89 96 95 16 2 2 84 86 89 17 2 2 103 109 90 18 2 2 92 96 101 19 2 2 97 98 100 20 2 2 102 104 103 21 3 1 93 98 110 22 3 1 98 104 112 23 3 1 98 105 99 24 3 1 87 132 120 25 3 1 94 110 116 26 3 2 95 126 143 27 3 2 100 126 140 28 3 2 103 124 140 29 3 2 94 135 130 30 3 2 99 111 150 end data.
Exercise example, model 1 (time and diet)
Let us first consider the model including diet as the group variable. The graph below suggests that the pulse rate is growing over time. The pulse rates may vary for the 2 diets and it is possible that the pulse rate is growing faster for the “green” diet than the “red” diet.
title "Exercise example model 1, time and diet". GLM time1 time2 time3 BY diet /WSFACTOR = time 3 /WSDESIGN=time /DESIGN=diet /EMMEANS=tables( time*diet) /PLOT = PROFILE( time*diet).
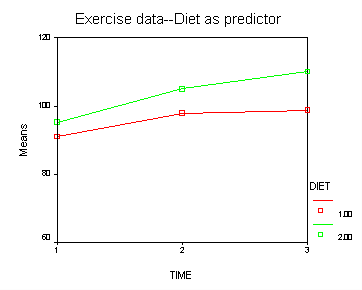
Looking at the results from the manova test the effect of time is significant but the interaction of time and diet is not significant. The between subject test of the effect of diet is also not significant. Consequently, in the graph we have lines that are not flat, in fact, they are actually increasing over time, which was expected since the effect of time was significant. Furthermore, the lines are approximately parallel which was anticipated since the interaction was not significant.

Exercise example, model 2 (time and exercise type)
Next, let us consider the model including exertype as the group variable.
title "Exercise example model 2, time and exertype". GLM time1 time2 time3 BY exertype /WSFACTOR = time 3 /WSDESIGN=time /DESIGN=exertype /EMMEANS=tables( time*exertype) /PLOT = profile( time*exertype).
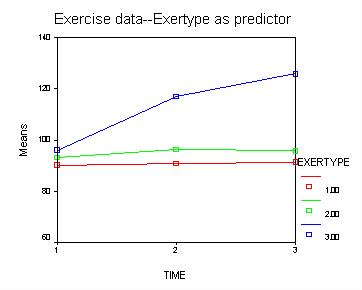
The interaction of time and exertype is significant as is the effect of time. The between subject test of the effect of exertype is also significant. Consequently, in the graph we have lines that are not parallel which we expected since the interaction was significant. Furthermore, we see that some of the lines that are rather far apart and at least one line is not horizontal which was anticipated since exertype and time were both significant. The output for this analysis is omitted.
Further Issues
Missing Data
- Compare GLM and Mixed on Missing Data
Variance-Covariance Structures
- Discuss “univariate” vs. “multivariate” tests.
- Discuss “sphericity” and test of sphericity.
Independence
As though analyzed using between subjects analysis.
s2 0 s2 0 0 s2
Compound Symmetry
The univariate tests assumes that the variance-covariance structure has compound symmetry. There is a single Variance (represented by s2) for all 3 of the time points and there is a single covariance (represented by s1) for each of the pairs of trials. This is illustrated below.
s2 s1 s2 s1 s1 s2
Unstructured
The manova tests assumes that each variance and covariance is unique, see below, referred to as an unstructured
covariance matrix. Each trial has its own variance (e.g. s12 is the variance of trial 1) and each pair of trials has its own covariance (e.g. s21 is the covariance of trial 1 and trial2).
s12 s21 s22 s31 s32 s32
We can use the sphericity test to indicate which is most appropriate: the manova or the univariate test. The null hypothesis test of the test of sphericity is: the variance-covariance structure has the Huynh-Feldt structure, so called Type H structure. If the sphericity test is not significant then we can not reject that null hypothesis that the variance-covariance structure has Type H structure. A Type H structure is a variance-covariance structure more general than compound symmetry structure that allows the use of the univariate tests. If, however, the sphericity test is significant then we reject that the variance-covariance structure has a Type H structure and it is most appropriate to use the results from the manova test or alternatively use the corrections for the univariate test. It is very important, however, to note that the sphericity test is overly sensitive. It is very likely to reject compound symmetry when the data only slightly deviates from compound symmetry, so in actuality this test could be very deceiving and may be best ignored.
Autoregressive
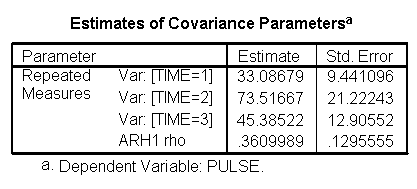
Another common covariance structure which is frequently observed in repeated measures data is an autoregressive structure, which recognizes that observations which are more proximate are more correlated than measures that are more distant
s2 sr s2 sr2 sr s2
Huynh-Feldt Variances
This is a circular matrix that satisfies the condition: si2 + sj2 – sij = 2l.
s12
(s12+ s22)/2 – l s22 (s12+ s32)/2 – l (s22+ s32)/2 – l s32
However, we cannot use this kind of covariance structure in a traditional repeated measures analysis, but we can use the MIXED command for such an analysis.
For a complete list of all variance-covariance structures that SPSS supports in the mixed command please see refer to the SPSS manual.
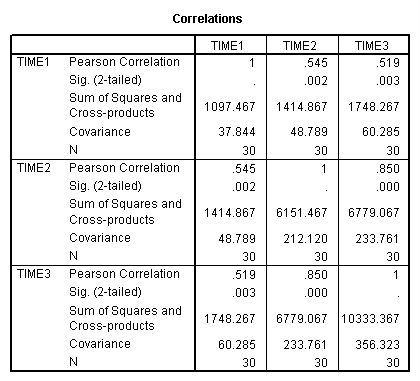
Let’s look at the correlations, variances and covariances for the exercise data.
CORRELATIONS /VARIABLES=time1 time2 time3 /STATISTICS XPROD.
Exercise example, model 2 using MIXED Command
Even though we are very impressed with our results so far, we are not completely convinced that the variance-covariance structure really has compound symmetry. In order to compare models with different variance-covariance structures we have to use proc mixed and try the different structures that we think our data might have. However, in order to use proc mixed we must reshape our data from its wide form to a long form.
VARSTOCASES /MAKE pulse from time1 TO time3 /INDEX = time(3). print / id exertype diet time pulse. execute.
Looking at the first 14 observations of the long dataset.
1 1.00 1.00 1 85.00
1 1.00 1.00 2 85.00
1 1.00 1.00 3 88.00
2 1.00 1.00 1 90.00
2 1.00 1.00 2 92.00
2 1.00 1.00 3 93.00
3 1.00 1.00 1 97.00
3 1.00 1.00 2 97.00
3 1.00 1.00 3 94.00
4 1.00 1.00 1 80.00
4 1.00 1.00 2 82.00
4 1.00 1.00 3 83.00
5 1.00 1.00 1 91.00
5 1.00 1.00 2 92.00
Compound Symmetry
The first model we will look at is one using compound symmetry for the variance-covariance structure. This model should confirm the results of the univariate tests that we obtained through glm and we will be able to obtain fit statistics that we will use for comparisons with our models that assume other variance-covariance structures.
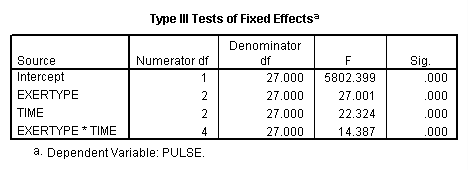
title "model 2, compound symmetry". MIXED pulse BY exertype time /FIXED = exertype time exertype*time /REPEATED = time | SUBJECT(id) COVTYPE(cs).

Unstructured
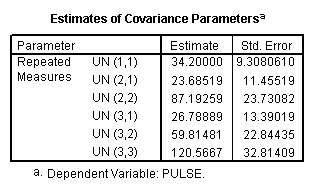
We now try an unstructured covariance matrix.
title "model 2, unstructured". MIXED pulse BY exertype time /FIXED = exertype time exertype*time /REPEATED = time | SUBJECT(id) COVTYPE(un).

Autoregressive
From previous studies we suspect that our data might actually have an auto-regressive variance-covariance structure so this is the model we will look at next. However, for our data the auto-regressive variance-covariance structure does not fit our data much better than the compound symmetry does (AIC of 594.8 vs. 594.1).
title "model 2, autoregressive". MIXED pulse BY exertype time /FIXED = exertype time exertype*time /REPEATED = time | SUBJECT(id) COVTYPE(ar1).


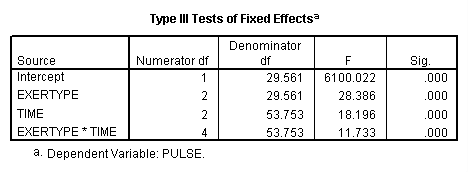
These results are exactly the same as those from the compound symmetry model. It is very important to explore different variance-covariance structures where we have fit statistics indicating how well the models fit compared to each other.
Model comparison (comparing to Compound Symmetry)
| Model | AIC | -2RLL | Parms (df + 1) | Diff -2RLL (vs. CS) | Diff in df (vs. CS) | p value for Diff (from a chi square dist) |
| Compound Symmetry | 594.8 | 590.8 | 2 | |||
| Unstructured | 589.7 | 577.7 | 6 | 13.1 | 4 | .01 |
| Autoregressive | 594.1 | 590.1 | 2 | .7 | 0 | na |
| (from SAS PROC MIXED) Autoregressive Heterogenous Variances | 587.8 | 579.8 | 4 | 11 | 2 | 0.027 |
The two most promising structures are Autoregressive Heterogeneous Variances and Unstructured.
Exercise example, model 3 (time, diet and exertype) Using the GLM command
Looking at models including only diet or exertype separately does not answer all our questions. We would also like to know if the people on the low-fat diet who engage in running have lower pulse rates than the people participating in the not low-fat diet who are not running. In order to address these types of questions we need to look at a model that includes the interaction of diet and exertype. Let us first look at the model including both diet and exertype using the glm command which means we have to use the wide data again. If we are not satisfied with the choice of compound symmetry or unstructured variance-covariance structure then we can return to the mixed command.
In the graph of exertype by diet we see that for the low-fat diet (diet=1) group the pulse rate for the two exercise types: at rest and walking, are very close together and they are almost flat whereas the running group has a higher pulse rate that increases over time. For the not low-fat diet (diet=2) group the same two exercise types: at rest and walking, are also very close together and almost flat. For this group, however, the pulse rate for the running group increases greatly over time and the increase is much steeper than the increase of the running group in the low-fat diet group.
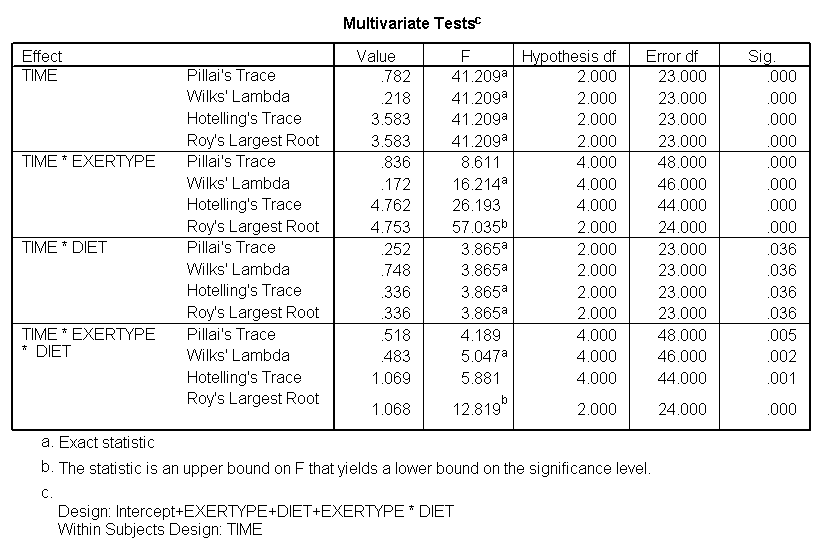
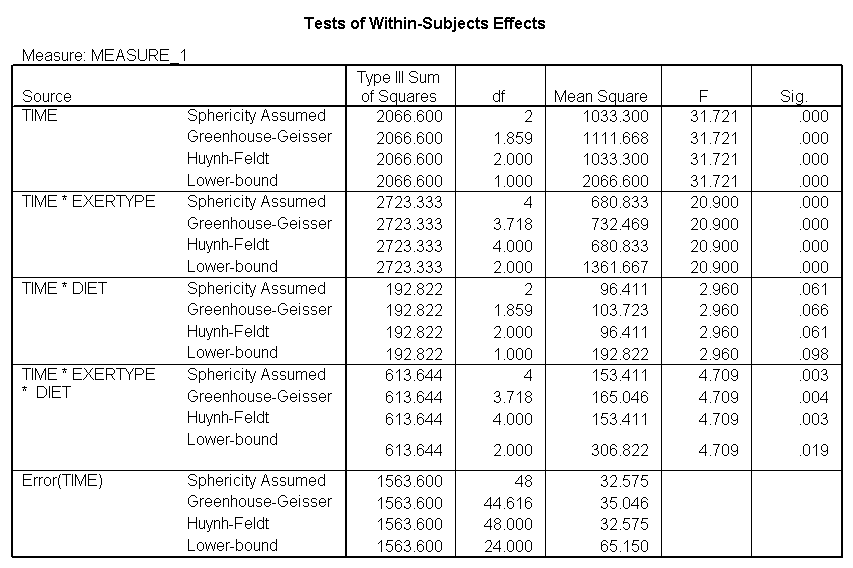
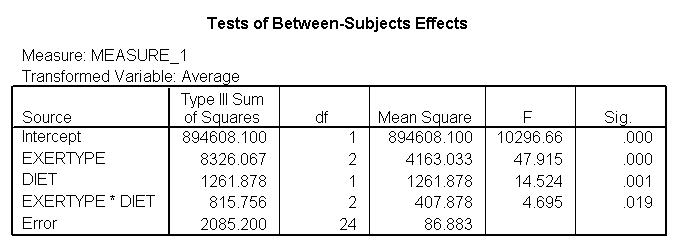
The test of sphericity is not significant so it is appropriate to look at the results from the univariate tests. The univariate tests indicate that there is a three-way interaction between diet, exertype and time. In other words, the pulse rate will depend on which diet you follow, the exercise type you engage in and at what time during the exercise that you measure the pulse. The interactions of time and exertype and diet and exertype are also significant as are the main effects of diet and exertype.
title "model 3, time exertype and diet". GLM time1 time2 time3 BY exertype diet /WSFACTOR=time 3 /WSDESIGN=time /PLOT = profile(time*exertype*diet ) .
Looking at the graphs of exertype by diet.
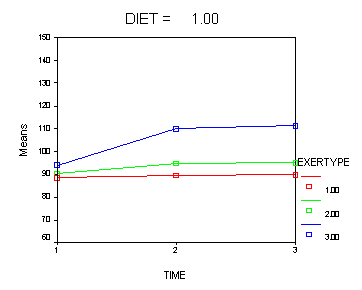
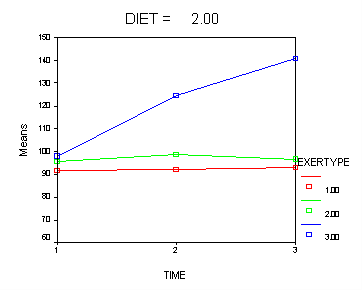

Exercise example, model 3 (time, diet and exertype) Using the MIXED command
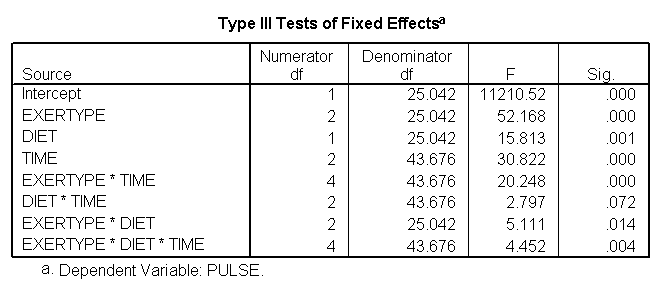
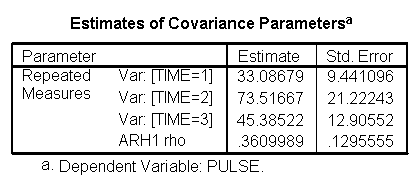
For the mixed model we will use the autoregressive heterogeneous variances variance-covariance structure since we previously observed that this is the structure that appears to fit the data the best (see discussion of variance-covariance structures). We do not expect to find a great change in which factors will be significant but we do expect to have a model that has a better fit than the glm model. The graphs are exactly the same as the glm model and we find that the same factors are significant. However, since the model has a better fit we can be more confident in the estimate of the standard errors and therefore we can be more confident in the tests and in the findings of significant factors. The model has a better fit than the model which only includes exertype and time because both the -2Log Likelihood and the AIC has decrease dramatically. The -2 Log Likelihood decreased from 579.8 for the model including only exertype and time to 505.3 for the current model; the AIC decreased from 587.8 for the model including only exertype and time to 513.3 for the current model.
MIXED pulse BY exertype diet time
/FIXED = exertype diet time exertype*time diet*time diet*exertype
exertype*diet*time
/REPEATED = time | SUBJECT(id) COVTYPE(arh1).

Contrasts and interaction contrasts for model 3
From the graphs in the above analysis we see that the runners (exertype level 3) have a pulse rate that is increases much quicker than the pulse rates of the two other groups. We would like to know if there is a statistically significant difference between the changes over time in the pulse rate of the runners versus the change over time in the pulse rate of the walkers and the “rest-ers” (the people at rest) across diet groups and across time. Furthermore, we suspect that there might be a difference in pulse rate over time and across exercise type between the two diet groups. But to make matters even more complicated we would like to test if the runners in the low fat diet group are statistically significantly different from all the other groups (i.e. the runners in the non-low fat diet, the walkers and the “rest-ers” in both diet groups). Since we are being ambitious we also want to test if the runners in the low fat diet group (diet=1) are different from the runners in the non-low fat diet group (diet=2). These contrasts are all tested using the test subcommand.
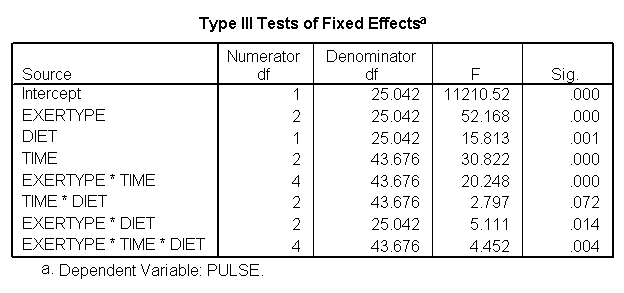
In the following example we are testing whether the pulse rate of exertype groups 1 and 2 is significantly different from the pulse rate of exertype group 3 (the runners). We are conducting this test across both time and diet. The results are contained in the table labeled “Contrast Estimates” which are the results of the test subcommand and here we note that the runners are indeed statistically significantly different from the other two groups (p < .0001). Since we are conducting a test involving exertype we have to include the coding scheme for all interactions which involve exertype. This is the reason why we have included the coding for the interaction diet*exertype, exertype*time and exertype*time*diet in the test subcommand. Note: The only change in the results from the model in the above example is the inclusion of the “Contrast Estimates” table and we will therefore omit them in the subsequent examples.
*exertype 12 v 3.
*include all interactions involving exertype.
MIXED pulse BY exertype time diet
/FIXED = exertype diet time exertype*time diet*time diet*exertype
exertype*diet*time
/REPEATED = time | SUBJECT(id) COVTYPE(arh1)
/test= 'exer 12 v 3' exertype -1/2 -1/2 1
exertype*diet -1/4 -1/4
-1/4 -1/4
1/2 1/2
exertype*time -1/6 -1/6 -1/6
-1/6 -1/6 -1/6
1/3 1/3 1/3
exertype*time*diet
-1/12 -1/12
-1/12 -1/12
-1/12 -1/12
-1/12 -1/12
-1/12 -1/12
-1/12 -1/12
1/6 1/6
1/6 1/6
1/6 1/6.


In the following example we are testing if exertype group 1 is different from exertype group 2 across both time and diet. From the results we conclude that they are not statistically significantly different from each other at the 0.05 level (p = 0.07).
*exertype 1 v 2.
*include all interactions involving exertype.
MIXED pulse BY exertype time diet
/FIXED = exertype diet time exertype*time diet*time diet*exertype
exertype*diet*time
/REPEATED = time | SUBJECT(id) COVTYPE(arh1)
/test= 'exer 1 v 2' exertype -1 1 0
exertype*diet -1/2 -1/2
1/2 1/2
0 0
exertype*time -1/3 -1/3 -1/3
1/3 1/3 1/3
0 0 0
exertype*time*diet
-1/6 -1/6
-1/6 -1/6
-1/6 -1/6
1/6 1/6
1/6 1/6
1/6 1/6
0 0
0 0
0 0.

In the following example we are testing if there is a significant difference between the two diets across time and exertype. From the results we conclude that the two diets are indeed statistically significantly different (p = 0.001).
*diet 1 v 2.
*include all interactions involving diet.
MIXED pulse BY exertype time diet
/FIXED = exertype diet time exertype*time diet*time diet*exertype
exertype*diet*time
/REPEATED = time | SUBJECT(id) COVTYPE(arh1)
/test= 'diet 1 v 2' diet -1 1
exertype*diet -1/3 1/3
-1/3 1/3
-1/3 1/3
time*diet -1/3 1/3
-1/3 1/3
-1/3 1/3
exertype*time*diet
-1/9 1/9
-1/9 1/9
-1/9 1/9
-1/9 1/9
-1/9 1/9
-1/9 1/9
-1/9 1/9
-1/9 1/9
-1/9 1/9.

In the following example we are testing if there is a difference across diets between the differences of exertype group 1 and 2 versus exertype group 3. This kind of contrast is known as an interaction contrast and for more details about these type of interactions please refer to Design and Analysis by G. Keppel. From the results we see that there is indeed a significant differences across diets between exertype group 1 and 2 and exertype group 3 (p = 0.004).
*diet 1 v 2 & exertype 12 v 3.
*include all interactions including exertype*diet.
MIXED pulse BY exertype time diet
/FIXED = exertype diet time exertype*time diet*time diet*exertype
exertype*diet*time
/REPEATED = time | SUBJECT(id) COVTYPE(arh1)
/test= 'diet 1 v 2 and exertype 12 v 3'
exertype*diet -1/2 1/2
-1/2 1/2
1 -1
exertype*time*diet
-1/6 1/6
-1/6 1/6
-1/6 1/6
-1/6 1/6
-1/6 1/6
-1/6 1/6
1/3 -1/3
1/3 -1/3
1/3 -1/3.

In the following example we are testing the difference between the diets for exertype group 3 (the runners). From the results we see that there is a statistically significant difference between the diets (p < 0.001).
*diet 1 v 2 for runners only (exertype group 3).
*include all interactions invovling diet.
MIXED pulse BY exertype time diet
/FIXED = exertype diet time exertype*time diet*time diet*exertype
exertype*diet*time
/REPEATED = time | SUBJECT(id) COVTYPE(arh1)
/test= 'diet 1 v 2 runners only' diet 1 -1
exertype*diet 0 0
0 0
1 -1
time*diet 1/3 -1/3
1/3 -1/3
1/3 -1/3
exertype*time*diet
0 0
0 0
0 0
0 0
0 0
0 0
1/3 -1/3
1/3 -1/3
1/3 -1/3.

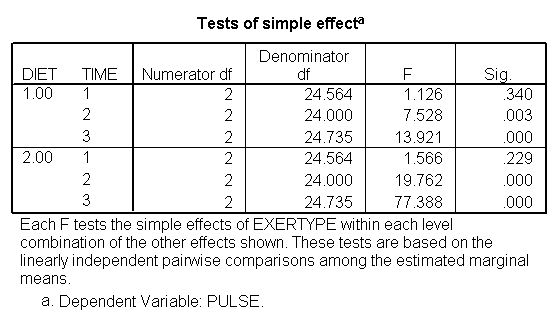
It is also possible to look at the differences among groups at each level of another variable and in order to do so we have to utilize the emmeans subcommand with the compare option. In the following example, the first emmeans subcommand tests for differences among the exertype groups at each level of diet across all levels of time; the second emmeans subcommand tests for differences in groups of exertype for each time point across both levels of diet; the third emmeans subcommand tests for differences in groups of exertype for each combination of time and diet levels. The results of the first emmeans subcommand indicate that there is a differences in the means for each level of exertype when we are considering only the people in diet = 1 (p < 0.001) and when we are considering only the people in diet = 2 (p < 0.001). The results of the second emmeans subcommand indicate that at time = 1 there is no differences in the means of the pulse rate for the different exertype groups; at time = 2 there is a difference among the means of the exertype groups (p < 0.001); at time = 3 there is also a difference among the means of pulse rate of the exertype groups (p < 0.001). The results of the third emmeans subcommand indicates that for diet = 1 and time = 1 there is no significant difference across the exertype groups (p = .34); for diet = 1 and time = 2 there is a significant difference across the exertype groups (p = 0.003); for diet = 1 and time = 3 there is a significant difference across the exertype groups(p < 0.001). The results of the third emmeans subcommand also indicates that for diet = 2 and time = 1 there is no significant difference across the exertype groups (p = .229); for diet = 2 and time = 2 there is a significant difference across the exertype groups (p < 0.001); for diet = 2 and time = 3 there is a significant difference across the exertype groups(p < 0.001). To summarize these results we could say that at the first time point the three exertype groups have mean pulse rates that are not significantly different regardless of which diet they are following. For the other time points there are significant differences between the mean pulse rates for the three exertype groups and that these differences exists in both diet groups.
*The first emmeans subcommand is testing the differences among
exertype for each level of diet.
*The second emmeans subcommand is testing for differences at each
time point.
*The 3rd emmeans subcommand tests for differences in groups of
exertype for each combination of time and diet levels.
MIXED pulse BY exertype diet time
/FIXED = exertype diet time exertype*time diet*time diet*exertype
exertype*diet*time
/REPEATED = time | SUBJECT(id) COVTYPE(arh1)
/emmeans = tables(exertype*diet) compare(exertype)
/emmeans = tables(exertype*time) compare(exertype)
/emmeans = tables(exertype*diet*time) compare(exertype).


Unequally Spaced Time Points
Modeling Time as a Linear Predictor of Pulse
We have another study which is very similar to the one previously discussed except that in this new study the pulse measurements were not taken at regular time points. In this study a baseline pulse measurement was obtained at time = 0 for every individual in the study. However, subsequent pulse measurements were taken at less regular time intervals. The second pulse measurements were taken at approximately 2 minutes (120 seconds); the third pulse measurement was obtained at approximately 5 minutes (300 seconds); and the fourth and final pulse measurement was obtained at approximately 10 minutes (600 seconds). The data for this study is displayed below in the study2 data file.
data list free / id timec exertype diet pulse time. begin data. 1 1 1 1 90 0 1 2 1 1 92 228 1 3 1 1 93 296 1 4 1 1 93 639 2 1 1 1 90 0 2 2 1 1 92 56 2 3 1 1 93 434 2 4 1 1 93 538 3 1 1 1 97 0 3 2 1 1 97 150 3 3 1 1 94 295 3 4 1 1 94 541 4 1 1 1 80 0 4 2 1 1 82 121 4 3 1 1 83 256 4 4 1 1 83 575 5 1 1 1 91 0 5 2 1 1 92 161 5 3 1 1 91 252 5 4 1 1 91 526 6 1 1 2 83 0 6 2 1 2 83 73 6 3 1 2 84 320 6 4 1 2 84 570 7 1 1 2 87 0 7 2 1 2 88 40 7 3 1 2 90 325 7 4 1 2 90 730 8 1 1 2 92 0 8 2 1 2 94 205 8 3 1 2 95 276 8 4 1 2 95 761 9 1 1 2 97 0 9 2 1 2 99 57 9 3 1 2 96 244 9 4 1 2 96 695 10 1 1 2 100 0 10 2 1 2 97 143 10 3 1 2 100 296 10 4 1 2 100 722 11 1 2 1 86 0 11 2 2 1 86 83 11 3 2 1 84 262 11 4 2 1 84 566 12 1 2 1 93 0 12 2 2 1 103 116 12 3 2 1 104 357 12 4 2 1 104 479 13 1 2 1 90 0 13 2 2 1 92 191 13 3 2 1 93 280 13 4 2 1 93 709 14 1 2 1 95 0 14 2 2 1 96 112 14 3 2 1 100 219 14 4 2 1 100 367 15 1 2 1 89 0 15 2 2 1 96 96 15 3 2 1 95 339 15 4 2 1 95 639 16 1 2 2 84 0 16 2 2 2 86 92 16 3 2 2 89 351 16 4 2 2 89 508 17 1 2 2 103 0 17 2 2 2 109 196 17 3 2 2 114 213 17 4 2 2 120 634 18 1 2 2 92 0 18 2 2 2 96 117 18 3 2 2 101 227 18 4 2 2 101 614 19 1 2 2 97 0 19 2 2 2 98 70 19 3 2 2 100 295 19 4 2 2 100 515 20 1 2 2 102 0 20 2 2 2 104 165 20 3 2 2 103 302 20 4 2 2 103 792 21 1 3 1 93 0 21 2 3 1 98 100 21 3 3 1 110 396 21 4 3 1 115 498 22 1 3 1 98 0 22 2 3 1 104 104 22 3 3 1 112 310 22 4 3 1 117 518 23 1 3 1 98 0 23 2 3 1 105 148 23 3 3 1 118 208 23 4 3 1 121 677 24 1 3 1 87 0 24 2 3 1 122 171 24 3 3 1 127 320 24 4 3 1 133 633 25 1 3 1 94 0 25 2 3 1 110 57 25 3 3 1 116 268 25 4 3 1 119 657 26 1 3 2 95 0 26 2 3 2 126 163 26 3 3 2 143 382 26 4 3 2 147 501 27 1 3 2 100 0 27 2 3 2 126 70 27 3 3 2 140 347 27 4 3 2 148 737 28 1 3 2 103 0 28 2 3 2 124 61 28 3 3 2 140 263 28 4 3 2 143 588 29 1 3 2 94 0 29 2 3 2 135 164 29 3 3 2 130 353 29 4 3 2 137 560 30 1 3 2 99 0 30 2 3 2 111 114 30 3 3 2 140 362 30 4 3 2 148 501 end data.
In order to get a better understanding of the data we will look at a scatter plot of the data with lines connecting the points for each individual.
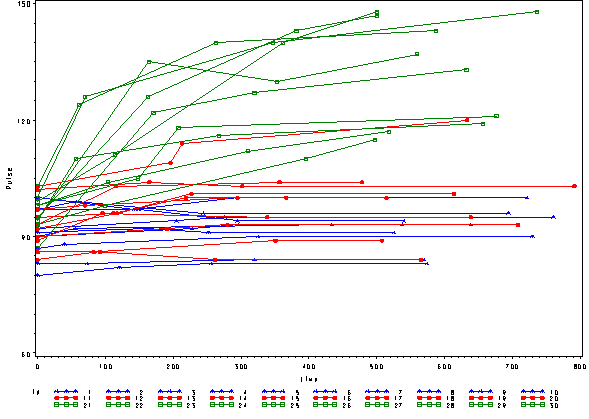
This is a situation where multilevel modeling excels for the analysis of data with irregularly spaced time points. The multilevel model with time as a linear effect is illustrated in the following equations.
Level 1 (time): Pulse = β0j + β1j (Time) + rij
Level 2 (person): β0j = γ00 + γ01(Exertype) + u0j Level 2 (person): β1j = γ10 + γ11(Exertype) + u1j
Substituting the level 2 model into the level 1 model we get the following single equations. Note: The random components have been placed in square brackets.
Pulse = γ00 + γ01(Exertype) + γ10(Time) + γ11(Exertype*time) + [ u0j + u1j(Time) + rij ]
Since this model contains both fixed and random components, it can be analyzed in the mixed command as shown below.
*linear model. mixed pulse with time by exertype /fixed = time exertype time*exertype /random = intercept time | subject(id).



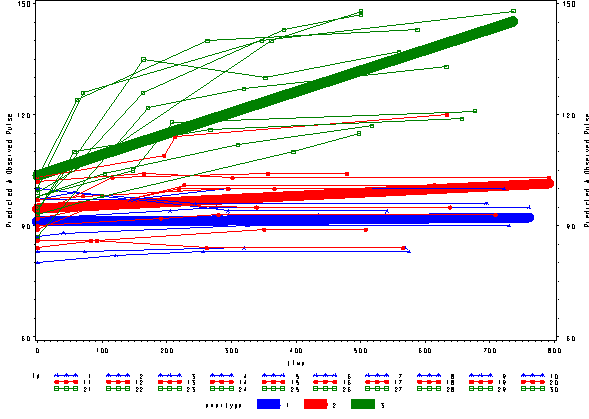
In order to access how well the model with time as a linear effect fits the model we have plotted the predicted and the observed values in one plot. As we can easily see the this model is not an optimal model since the green line is fitting curved data with a straight line. All the predicted lines are straight lines since we fitted time to as a linear effect.
Note: Currently it is not possible to produce these types of graphs with the mixed command in SPSS version 11. The graphs in this section were all produced by SAS. Please refer to the seminar Repeated Measures using SAS for the code.
Modeling Time as a Quadratic Predictor of Pulse
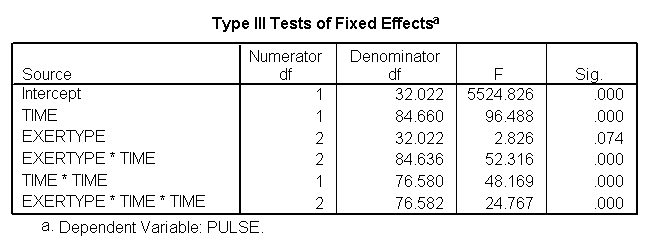
To model the quadratic effect of time, we add time*time to the model. We see that term is significant.
*quadratic mode. mixed pulse with time by exertype /fixed = time exertype time*exertype time*time /random = intercept time | subject(id).

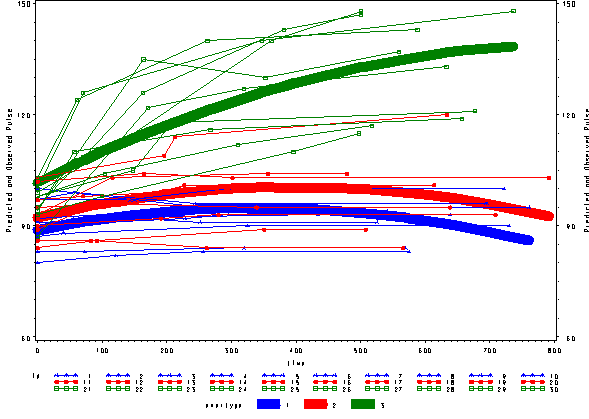
Again, we can plot the predicted values against the actual values of pulse. We see that this model fits better, but it appears that the predicted values for the green group have too little curvature and the red and blue group have too much curvature.
Modeling Time as a Quadratic Predictor of Pulse, Interacting by Exertype
We can include an interaction of time*time*exertype to indicate that the different exercises not only show different linear trends over time, but that they also show different quadratic trends over time, as shown below. The time*time*exertype term is significant.
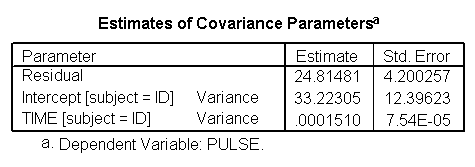
*Modeling time as quadratic and interacting with exertype. mixed pulse with time by exertype /fixed = time exertype time*exertype time*time time*time*exertype /random = intercept time | subject(id).


Below we see the predicted and actual values and see that this model fits much better. The green curve hugs the data from the green group much better and the blue and red groups are much flatter, fitting their data much better as well.
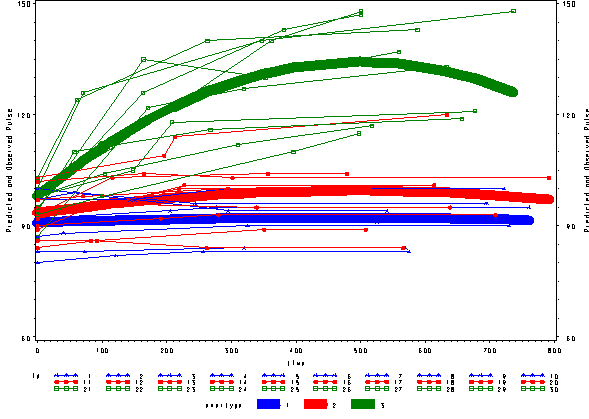
For more information:
- SPSS Library: Comparing Methods of Analyzing Repeated Measures Data
- SPSS Textbook Examples: Design and Analysis- A Researchers Handbook (3rd Edition)
- SPSS Library: An Overview of SPSS GLM (courtesy of SPSS)
- SPSS Library: MANOVA and GLM (courtesy of SPSS)
- SPSS Library: Understanding and Interpreting Parameter Estimates in Regression and ANOVA (courtesy of SPSS)
- SPSS Library: How do I handle interactions of continuous and categorical variables?
- SPSS Library: Advanced Issues in Using and Understanding SPSS MANOVA (courtesy of SPSS)