Using postgr3 with multiple regression, no interactions
Using postgr3 with multiple regression, with interactions
More on options when using postgr3
postgr3 with other estimation models
This page will illustrate the use of postgr3
for making graphs after estimation commands. You can obtain postgr3 over the
internet by typing search postgr3 (see
How can I use the search command to search for programs and get additional
help? for more information about using search).
NOTE! You must install the
spostado utilities before postgr3 will work
properly. You can download spostado by typing search spostado
We also recommend obtaining the latest version of xi3 which compliments postgr3. You can download xi3 from within Stata by typing search xi3 (see How can I use the search command to search for programs and get additional help? for more information about using search). For postgr3 to work properly you need Stata 8 and your Stata should be up to date (i.e., you need to have recently run the update all command in Stata).
In these examples, we will use the hsb2 data file which you can get like this.
use https://stats.idre.ucla.edu/stat/stata/notes/hsb2, clear
Using postgr3 with multiple regression, no interactions
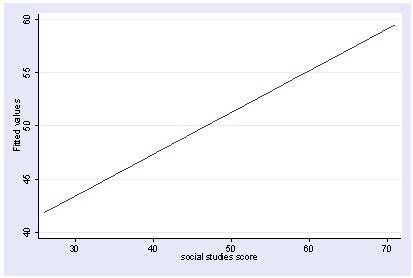
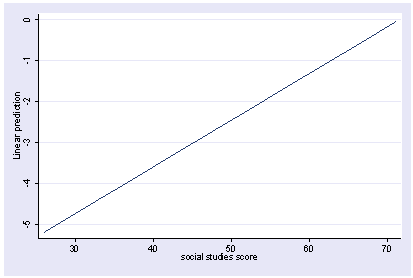
We can do a multiple regression and then show how the predicted values vary as a function of socst holding other variables constant at their mean. Note how we precede the regress command with xi3. This is because xi3 and postgr3 work together as a team.
xi3: regress read female ses socst science Source | SS df MS Number of obs = 200 -------------+------------------------------ F( 4, 195) = 56.33 Model | 11214.2588 4 2803.5647 Prob > F = 0.0000 Residual | 9705.16119 195 49.7700574 R-squared = 0.5361 -------------+------------------------------ Adj R-squared = 0.5266 Total | 20919.42 199 105.122714 Root MSE = 7.0548 ------------------------------------------------------------------------------ read | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- female | -.3283535 1.026784 -0.32 0.749 -2.35338 1.696673 ses | .4767216 .7469296 0.64 0.524 -.9963759 1.949819 socst | .3941527 .054806 7.19 0.000 .2860642 .5022413 science | .4418034 .0584274 7.56 0.000 .3265726 .5570343 _cons | 7.866209 3.125707 2.52 0.013 1.701677 14.03074 ------------------------------------------------------------------------------ postgr3 socst Variables left asis: socst Holding female constant at .545 Holding ses constant at 2.055 Holding science constant at 51.85
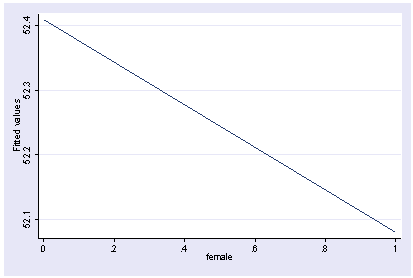
We can show how the predicted values vary as a function of female holding other variables constant at their mean.
postgr3 female Variables left asis: female Holding ses constant at 2.055 Holding socst constant at 52.405 Holding science constant at 51.85
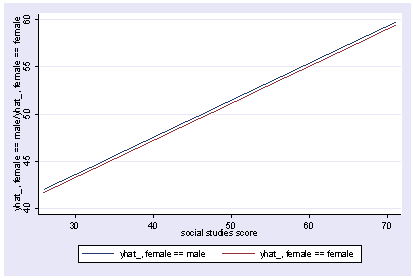
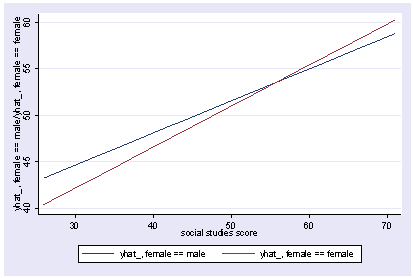
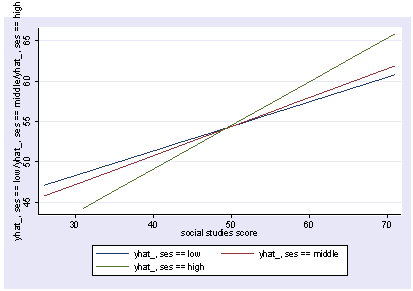
We can also show how the predicted values vary as a function of socst and female, holding other variables constant at their mean.
postgr3 socst, by(female) Variables left asis: socst female Holding ses constant at 2.055 Holding science constant at 51.85
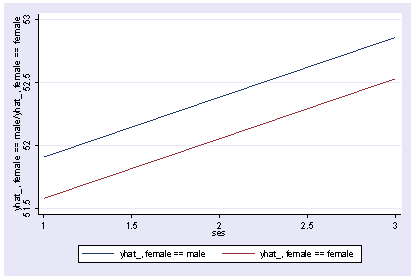
Or we can show how the predicted values vary by ses and female, holding other variables constant at their mean.
postgr3 ses, by(female) Variables left asis: ses female Holding socst constant at 52.405 Holding science constant at 51.85
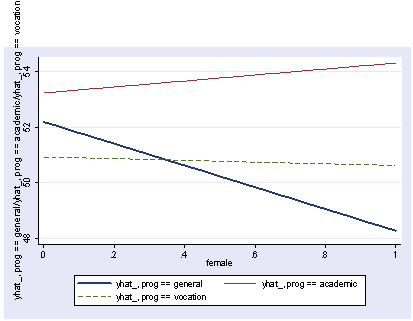
Using postgr3 with multiple regression, with interactions
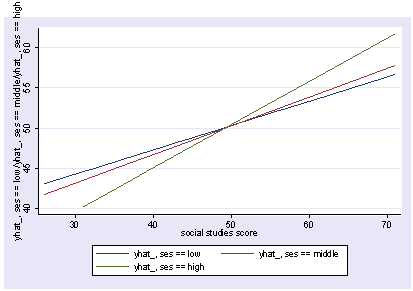
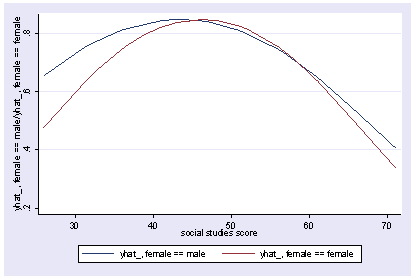
If we wish to include categorical variables (especially interactions), we then use xi3 for coding the categorical variables. Although it permits a wide variety of coding schemes (see help xi3) we will just use regular dummy coding indicated by the i. prefix. We wull run the above model with an interaction of socst and female and show the graph of the interaction, holding other variables constant at their mean.
xi3: regress read i.female*socst ses science i.female _Ifemale_0-1 (naturally coded; _Ifemale_0 omitted) i.female*socst _IfemXsocst_# (coded as above) Source | SS df MS Number of obs = 200 -------------+------------------------------ F( 5, 194) = 45.29 Model | 11267.2025 5 2253.4405 Prob > F = 0.0000 Residual | 9652.2175 194 49.7536985 R-squared = 0.5386 -------------+------------------------------ Adj R-squared = 0.5267 Total | 20919.42 199 105.122714 Root MSE = 7.0536 ------------------------------------------------------------------------------ read | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- _Ifemale_1 | -5.363727 4.988108 -1.08 0.284 -15.20161 4.474156 socst | .3453355 .0724033 4.77 0.000 .2025369 .4881342 _IfemXsocs~1 | .096356 .0934081 1.03 0.304 -.0878697 .2805817 ses | .5139953 .7476804 0.69 0.493 -.9606305 1.988621 science | .4425136 .0584219 7.57 0.000 .32729 .5577372 _cons | 10.27643 3.902047 2.63 0.009 2.580547 17.97231 ------------------------------------------------------------------------------ postgr3 socst, by(female) Variables left asis: socst _Ifemale_1 _IfemXsocst_1 Holding ses constant at 2.055 Holding science constant at 51.85
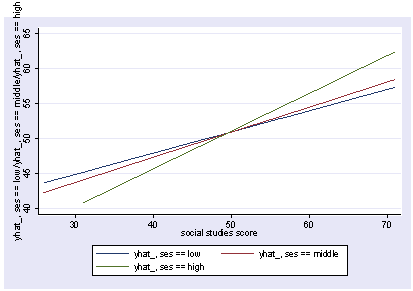
We can use reverse helmert coding on ses (which compares 2 vs 1 and 3 vs 12) and interact that by socst and then use postgr3 to show this interaction, holding other variables constant.
xi3: regress read r.ses*socst female science
r.ses _Ises_1-3 (naturally coded; _Ises_1 omitted)
r.ses*socst _IsesXsocst_# (coded as above)
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 7, 192) = 32.99
Model | 11421.7692 7 1631.68131 Prob > F = 0.0000
Residual | 9497.65083 192 49.4669314 R-squared = 0.5460
-------------+------------------------------ Adj R-squared = 0.5294
Total | 20919.42 199 105.122714 Root MSE = 7.0333
------------------------------------------------------------------------------
read | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Ises_2 | -2.790321 6.033969 -0.46 0.644 -14.6917 9.111058
_Ises_3 | -10.3084 6.228643 -1.65 0.100 -22.59375 1.976956
socst | .4011395 .0560911 7.15 0.000 .2905057 .5117734
_IsesXsocs~2 | .0552476 .1203009 0.46 0.647 -.1820334 .2925285
_IsesXsocs~3 | .2089692 .1119203 1.87 0.063 -.011782 .4297204
female | -.196438 1.033133 -0.19 0.849 -2.234185 1.841309
science | .4375687 .0582931 7.51 0.000 .3225916 .5525459
_cons | 8.327722 3.304713 2.52 0.013 1.809518 14.84593
------------------------------------------------------------------------------
postgr3 socst, by(ses)
Variables left asis: socst _Ises_2 _Ises_3 _IsesXsocst_2 _IsesXsocst_3
Holding female constant at .545
Holding science constant at 51.85
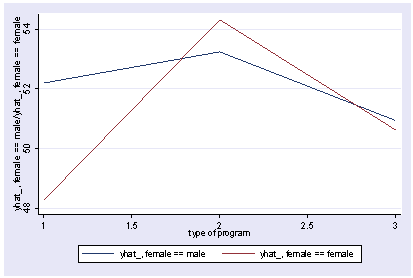
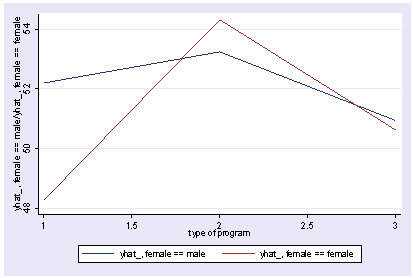
We can use reverse helmert coding on prog and look at the interaction with female using xi3 and then show the interaction with postgr3.
xi3: regress read r.prog*i.female socst science r.prog _Iprog_1-3 (naturally coded; _Iprog_1 omitted) i.female _Ifemale_0-1 (naturally coded; _Ifemale_0 omitted) r.prog*i.female _IproXfem_#_# (coded as above) Source | SS df MS Number of obs = 200 -------------+------------------------------ F( 7, 192) = 36.05 Model | 11879.6717 7 1697.09595 Prob > F = 0.0000 Residual | 9039.74835 192 47.0820227 R-squared = 0.5679 -------------+------------------------------ Adj R-squared = 0.5521 Total | 20919.42 199 105.122714 Root MSE = 6.8616 ------------------------------------------------------------------------------ read | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- _Iprog_2 | 1.044267 1.826394 0.57 0.568 -2.558106 4.64664 _Iprog_3 | -1.78684 1.78787 -1.00 0.319 -5.313229 1.739548 _Ifemale_1 | -1.053392 1.058655 -1.00 0.321 -3.141479 1.034694 _IproXfe~2_1 | 5.005482 2.45381 2.04 0.043 .1655968 9.845368 _IproXfe~3_1 | 1.114799 2.312977 0.48 0.630 -3.447309 5.676906 socst | .339437 .0561575 6.04 0.000 .2286722 .4502018 science | .4448466 .0568237 7.83 0.000 .3327678 .5569255 _cons | 11.27162 3.240477 3.48 0.001 4.880115 17.66313 ------------------------------------------------------------------------------ postgr3 prog, by(female) Variables left asis: _Iprog_2 _Iprog_3 _Ifemale_1 _IproXfem_2_1 _IproXfem_3_1 Holding socst constant at 52.405 Holding science constant at 51.85
More on options when using postgr3
Let us consider this regression model with an interaction term for ses and socst.
xi3: regress read r.ses*socst female science
r.ses _Ises_1-3 (naturally coded; _Ises_1 omitted)
r.ses*socst _IsesXsocst_# (coded as above)
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 7, 192) = 32.99
Model | 11421.7692 7 1631.68131 Prob > F = 0.0000
Residual | 9497.65083 192 49.4669314 R-squared = 0.5460
-------------+------------------------------ Adj R-squared = 0.5294
Total | 20919.42 199 105.122714 Root MSE = 7.0333
------------------------------------------------------------------------------
read | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Ises_2 | -2.790321 6.033969 -0.46 0.644 -14.6917 9.111058
_Ises_3 | -10.3084 6.228643 -1.65 0.100 -22.59375 1.976956
socst | .4011395 .0560911 7.15 0.000 .2905057 .5117734
_IsesXsocs~2 | .0552476 .1203009 0.46 0.647 -.1820334 .2925285
_IsesXsocs~3 | .2089692 .1119203 1.87 0.063 -.011782 .4297204
female | -.196438 1.033133 -0.19 0.849 -2.234185 1.841309
science | .4375687 .0582931 7.51 0.000 .3225916 .5525459
_cons | 8.327722 3.304713 2.52 0.013 1.809518 14.84593
------------------------------------------------------------------------------
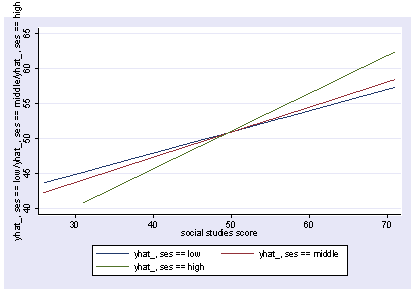
As we have seen, we can show the interaction with postgr3 like below.
postgr3 socst, by(ses) Variables left asis: socst _Ises_2 _Ises_3 _IsesXsocst_2 _IsesXsocst_3 Holding female constant at .545 Holding science constant at 51.85
We can use the x option to show the predicted values with other variables held constant at different values than the mean. For example, we can show the predicted values for females with science scores of 60.
postgr3 socst, by(ses) x(female=1 science=60) Variables left asis: socst _Ises_2 _Ises_3 _IsesXsocst_2 _IsesXsocst_3 Holding female constant at 1 Holding science constant at 60
If we use the x option to show the predicted values for females and make no reference to science, then science will be held at the overall mean of science (for males and females). Instead, we can use rest(grmean) to indicate that the rest of the variables should be held at the group mean as indicated by the x variable. So, if we did summarize if female==1 and got that mean for science it would be 50.69. As you see below, science is held constant at that value, the mean for females.
postgr3 socst, by(ses) x(female=1) rest(grmean) Variables left asis: socst _Ises_2 _Ises_3 _IsesXsocst_2 _IsesXsocst_3 Holding female constant at 1 Holding science constant at 50.697248
We can show a table of the predicted values using the table option, as shown below. Note that missing values are indicated where no observations were present (the graph is omitted to save space).
postgr3 socst, by(ses) x(female=1) rest(grmean) table
Variables left asis: socst _Ises_2 _Ises_3 _IsesXsocst_2 _IsesXsocst_3
Holding female constant at 1
Holding science constant at 50.697248
predict yhat_,
(option xb assumed; fitted values)
Means of Fitted values
social |
studies | ses
score | low middle high | Total
-----------+---------------------------------+----------
26 | 43.046452 41.692566 . | 42.595156
31 | 44.565746 43.488102 40.196571 | 42.93463
32 | 44.869606 . . | 44.869606
33 | 45.173466 . . | 45.173466
36 | 46.085045 45.283634 42.898834 | 45.286063
37 | 46.388905 . . | 46.388905
39 | . . 44.520191 | 44.520191
41 | 47.60434 47.07917 45.601097 | 47.117067
42 | . . 46.141548 | 46.141548
43 | 48.212059 . . | 48.212059
44 | 48.515919 . . | 48.515919
46 | 49.123638 48.874702 48.30336 | 48.825146
47 | . . 48.843811 | 48.843811
48 | 49.731358 . . | 49.731358
51 | 50.642933 50.670238 51.005619 | 50.695648
52 | . 51.029346 51.546074 | 51.28771
56 | 52.162231 52.465775 53.707882 | 52.787533
57 | 52.466091 . . | 52.466091
58 | . 53.183987 . | 53.183987
61 | 53.681526 54.261307 56.410145 | 55.202913
66 | 55.200825 56.056843 59.112404 | 57.604936
71 | 56.720119 57.852375 61.814667 | 59.691989
-----------+---------------------------------+----------
Total | 49.524473 51.040686 54.322879 | 51.636212
If we show the predicted values by 2 categorical variables, we might also want to show a table of the predicted values, for example broken down by prog and female as illustrated below.
xi3: regress read r.prog*i.female socst science
r.prog _Iprog_1-3 (naturally coded; _Iprog_1 omitted)
i.female _Ifemale_0-1 (naturally coded; _Ifemale_0 omitted)
r.prog*i.female _IproXfem_#_# (coded as above)
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 7, 192) = 36.05
Model | 11879.6717 7 1697.09595 Prob > F = 0.0000
Residual | 9039.74835 192 47.0820227 R-squared = 0.5679
-------------+------------------------------ Adj R-squared = 0.5521
Total | 20919.42 199 105.122714 Root MSE = 6.8616
------------------------------------------------------------------------------
read | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Iprog_2 | 1.044267 1.826394 0.57 0.568 -2.558106 4.64664
_Iprog_3 | -1.78684 1.78787 -1.00 0.319 -5.313229 1.739548
_Ifemale_1 | -1.053392 1.058655 -1.00 0.321 -3.141479 1.034694
_Ipr2Xfe1 | 5.005482 2.45381 2.04 0.043 .1655968 9.845368
_Ipr3Xfe1 | 1.114799 2.312977 0.48 0.630 -3.447309 5.676906
socst | .339437 .0561575 6.04 0.000 .2286722 .4502018
science | .4448466 .0568237 7.83 0.000 .3327678 .5569255
_cons | 11.27162 3.240477 3.48 0.001 4.880115 17.66313
------------------------------------------------------------------------------
postgr3 prog, by(female) table
Variables left asis: _Iprog_2 _Iprog_3 _Ifemale_1 _IproXfem_2_1 _IproXfem_3_1
Holding socst constant at 52.405
Holding science constant at 51.85
Means of Fitted values
type of | female
program | male female | Total
-----------+----------------------+----------
general | 52.198593 48.270859 | 50.103801
academic | 53.242859 54.32061 | 53.838188
vocation | 50.933884 50.623692 | 50.76638
-----------+----------------------+----------
Total | 52.418287 52.072804 | 52.229999
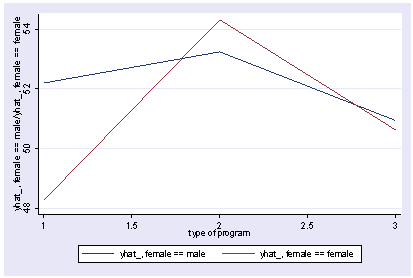
However, the table is not in the same orientation as the graph, so you can use the table2 option to swap the rows and columns of the table and to make it better correspond with the graph.
postgr3 prog, by(female) table2 Variables left asis: _Iprog_2 _Iprog_3 _Ifemale_1 _IproXfem_2_1 _IproXfem_3_1 Holding socst constant at 52.405 Holding science constant at 51.85
Means of Fitted values
| type of program
female | general academic vocation | Total
-----------+---------------------------------+----------
male | 52.198593 53.242859 50.933884 | 52.418287
female | 48.270859 54.32061 50.623692 | 52.072804
-----------+---------------------------------+----------
Total | 50.103801 53.838188 50.76638 | 52.229999
We can add graph options to make the graph look better. For example, below we add the clpattern() and the clwidth() options to control the line pattern and line width.
postgr3 female, by(prog) clpattern(l l dash ) clwidth(thick . .) Variables left asis: _Ifemale_1 _Iprog_2 _Iprog_3 _Ipr2Xfe1 _Ipr3Xfe1 Holding socst constant at 52.405 Holding science constant at 51.85
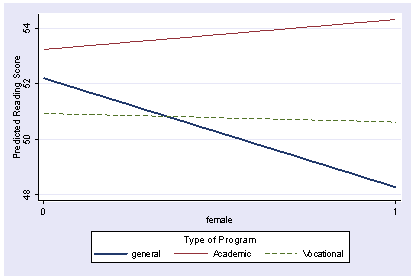
We can add additional graph options to make the graph look nicer. We add lagend options, and change the ytitle and labels for the x axis below to improve the look of the graph.
postgr3 female, by(prog) clpattern(l l dash ) clwidth(thick . .) /// legend(subtitle(Type of Program) order(1 "general" 2 "Academic" 3 "Vocational") rows(1) ) /// ytitle(Predicted Reading Score) xlabel(0 1) Variables left asis: _Ifemale_1 _Iprog_2 _Iprog_3 _Ipr2Xfe1 _Ipr3Xfe1 Holding socst constant at 52.405 Holding science constant at 51.85
Say we want to include a squared term, say socst and socst2.
gen socst2 = socst*socst
xi3: regress read r.prog*i.female socst socst2 science
r.prog _Iprog_1-3 (naturally coded; _Iprog_1 omitted)
i.female _Ifemale_0-1 (naturally coded; _Ifemale_0 omitted)
r.prog*i.female _IproXfem_#_# (coded as above)
Source | SS df MS Number of obs = 200
-------------+------------------------------ F( 8, 191) = 32.48
Model | 12057.4759 8 1507.18449 Prob > F = 0.0000
Residual | 8861.9441 191 46.3976131 R-squared = 0.5764
-------------+------------------------------ Adj R-squared = 0.5586
Total | 20919.42 199 105.122714 Root MSE = 6.8116
------------------------------------------------------------------------------
read | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Iprog_2 | .8859053 1.814874 0.49 0.626 -2.693866 4.465676
_Iprog_3 | -2.339243 1.79712 -1.30 0.195 -5.883994 1.205508
_Ifemale_1 | -.9018447 1.053779 -0.86 0.393 -2.980384 1.176695
_Ipr2Xfe1 | 4.74971 2.439411 1.95 0.053 -.061935 9.561356
_Ipr3Xfe1 | 1.508573 2.304899 0.65 0.514 -3.037751 6.054898
socst | -.4043657 .3840249 -1.05 0.294 -1.16184 .3531089
socst2 | .0074461 .0038037 1.96 0.052 -.0000565 .0149488
science | .4234667 .0574567 7.37 0.000 .3101355 .5367979
_cons | 29.99129 10.08915 2.97 0.003 10.09083 49.89176
------------------------------------------------------------------------------
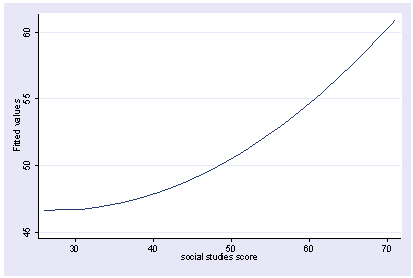
If we want to view the results as a function of socst, we would not want socst2 to be held constant. In fact, we would want that to vary as is, so we would include socst and socst2 in the asis option to prevent postgr3 from trying to hold them constant.
postgr3 socst, asis(socst socst2) Variables left asis: socst socst2 Holding _Iprog_2 constant at .15 Holding _Iprog_3 constant at -.08333333 Holding _Ifemale_1 constant at .545 Holding _IproXfem_2_1 constant at .085 Holding _IproXfem_3_1 constant at -.04666667 Holding science constant at 51.85
postgr3 with other estimation models
Although all of the examples up to now have used regression models via the regress command, postgr3 can be used with a wide variety of estimation commands, including logit, probit, ologit, mlogit, and more. Here are some examples.
We will create a variable called goodread which is 1 if the reading score is over 60.
gen goodread = read > 60
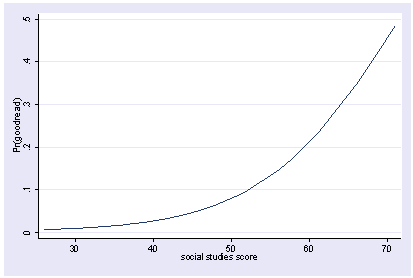
We can then use logit with and show the predicted values by socst. The y axis is showing predicted probabilities.
xi3: logit goodread i.female socst science i.female _Ifemale_0-1 (naturally coded; _Ifemale_0 omitted) Iteration 0: log likelihood = -109.04953 Iteration 1: log likelihood = -75.950592 Iteration 2: log likelihood = -69.751911 Iteration 3: log likelihood = -68.82564 Iteration 4: log likelihood = -68.792504 Iteration 5: log likelihood = -68.792448 Logit estimates Number of obs = 200 LR chi2(3) = 80.51 Prob > chi2 = 0.0000 Log likelihood = -68.792448 Pseudo R2 = 0.3692 ------------------------------------------------------------------------------ goodread | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- _Ifemale_1 | -.0075975 .4446729 -0.02 0.986 -.8791404 .8639453 socst | .1140219 .027665 4.12 0.000 .0597994 .1682443 science | .1479431 .0340121 4.35 0.000 .0812806 .2146056 _cons | -15.81825 2.477648 -6.38 0.000 -20.67435 -10.96215 ------------------------------------------------------------------------------ postgr3 socst Variables left asis: socst Holding _Ifemale_1 constant at .545 Holding science constant at 51.85
If we wished, we could show the predicted values as logits by specifying the predict option. The predict option accepts the same values as would follow the comma after the predict command.
postgr3 socst, predict(xb) Variables left asis: socst Holding _Ifemale_1 constant at .545 Holding science constant at 51.85
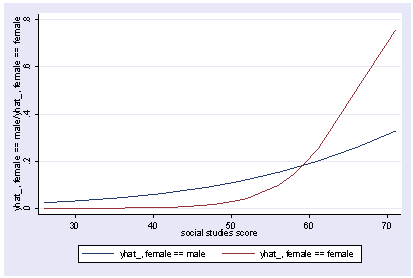
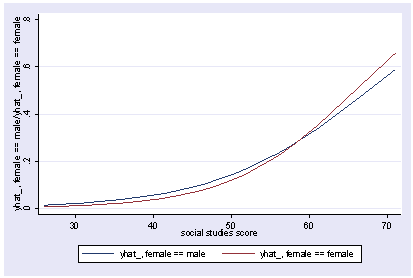
We can include an interaction of female and socst and show the predicted values holding science constant at its mean.
xi3: logit goodread i.female*socst science i.female _Ifemale_0-1 (naturally coded; _Ifemale_0 omitted) i.female*socst _IfemXsocst_# (coded as above) Iteration 0: log likelihood = -109.04953 Iteration 1: log likelihood = -75.075084 Iteration 2: log likelihood = -67.681437 Iteration 3: log likelihood = -65.89615 Iteration 4: log likelihood = -65.703276 Iteration 5: log likelihood = -65.700115 Iteration 6: log likelihood = -65.700114 Logit estimates Number of obs = 200 LR chi2(4) = 86.70 Prob > chi2 = 0.0000 Log likelihood = -65.700114 Pseudo R2 = 0.3975 ------------------------------------------------------------------------------ goodread | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- _Ifemale_1 | -9.307788 4.19752 -2.22 0.027 -17.53478 -1.0808 socst | .0662987 .0307774 2.15 0.031 .0059761 .1266214 _IfeXso | .1571849 .0698483 2.25 0.024 .0202846 .2940851 science | .1479992 .0339313 4.36 0.000 .081495 .2145033 _cons | -13.10211 2.579092 -5.08 0.000 -18.15704 -8.047181 ------------------------------------------------------------------------------ postgr3 socst, by(female) Variables left asis: socst _Ifemale_1 _IfemXsocst_1 Holding science constant at 51.85
We can include an interaction of 2 categorical variables and show the predicted probabilities along with a table.
xi3: logit goodread i.ses*i.female socst science i.ses _Ises_1-3 (naturally coded; _Ises_1 omitted) i.female _Ifemale_0-1 (naturally coded; _Ifemale_0 omitted) i.ses*i.female _IsesXfem_#_# (coded as above) Iteration 0: log likelihood = -109.04953 Iteration 1: log likelihood = -72.980799 Iteration 2: log likelihood = -66.566231 Iteration 3: log likelihood = -65.555596 Iteration 4: log likelihood = -65.512747 Iteration 5: log likelihood = -65.512645 Logit estimates Number of obs = 200 LR chi2(7) = 87.07 Prob > chi2 = 0.0000 Log likelihood = -65.512645 Pseudo R2 = 0.3992 ------------------------------------------------------------------------------ goodread | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- _Ises_2 | -1.062254 .9440273 -1.13 0.260 -2.912514 .7880054 _Ises_3 | -1.289494 1.022621 -1.26 0.207 -3.293795 .7148073 _Ifemale_1 | -1.164263 1.074516 -1.08 0.279 -3.270276 .9417497 _Ise2Xfe1 | .4015754 1.245133 0.32 0.747 -2.038841 2.841992 _Ise2Xfe1 | 2.195925 1.305186 1.68 0.092 -.3621935 4.754043 socst | .1279548 .0310952 4.11 0.000 .0670093 .1889003 science | .1330011 .0345899 3.85 0.000 .0652062 .2007959 _cons | -14.73353 2.553764 -5.77 0.000 -19.73881 -9.728241 ------------------------------------------------------------------------------ postgr3 ses, by(female) table2 Variables left asis: _Ises_2 _Ises_3 _Ifemale_1 _IsesXfem_2_1 _IsesXfem_3_1 Holding socst constant at 52.405 Holding science constant at 51.85---------------------------------------- | ses female | low middle high ----------+----------------------------- male | .243801 .100272 .0815519 female | .0914369 .0494117 .1994422 ----------------------------------------
We can create a 3 level variable for read called readcat that will be 1 if less than 40, 2 if between 40 and 60, and 3 if over 60. We can then use ologit to predict this 3 level variable.
generate readcat = read recode readcat 0/40=1 60/100=3 40/60=2
We then run ologit as shown below.
xi3: ologit readcat i.female*socst science
i.female _Ifemale_0-1 (naturally coded; _Ifemale_0 omitted)
Iteration 0: log likelihood = -180.15028
Iteration 1: log likelihood = -131.10376
Iteration 2: log likelihood = -125.59369
Iteration 3: log likelihood = -125.01305
Iteration 4: log likelihood = -125.00309
Iteration 5: log likelihood = -125.00309
Ordered logit estimates Number of obs = 200
LR chi2(4) = 110.29
Prob > chi2 = 0.0000
Log likelihood = -125.00309 Pseudo R2 = 0.3061
------------------------------------------------------------------------------
readcat | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Ifemale_1 | -1.37027 1.629177 -0.84 0.400 -4.563398 1.822858
socst | .1031981 .0242797 4.25 0.000 .0556107 .1507855
_Ife1Xso | .0234216 .0303904 0.77 0.441 -.0361425 .0829857
science | .1103603 .0217462 5.07 0.000 .0677386 .152982
-------------+----------------------------------------------------------------
_cut1 | 7.708743 1.391748 (Ancillary parameters)
_cut2 | 12.68828 1.676964
------------------------------------------------------------------------------
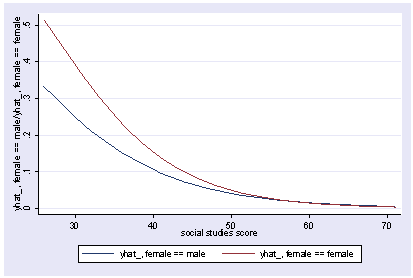
Since this model has multiple outcomes, we need to use the outcome option to indicate which outcome we want to graph when we use postgr3. Below we graph the first outcome (readcat=1).
postgr3 socst, by(female) outcome(1) Variables left asis: socst _Ifemale_1 _IfemXsocst_1 Holding science constant at 51.85
and we show the graph for readcat=2.
postgr3 socst, by(female) outcome(2) Variables left asis: socst _Ifemale_1 _IfemXsocst_1 Holding science constant at 51.85
and we show the graph for readcat=3.
postgr3 socst, by(female) outcome(3) Variables left asis: socst _Ifemale_1 _IfemXsocst_1 Holding science constant at 51.85
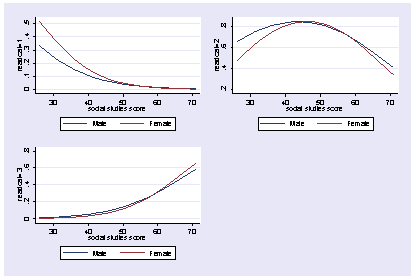
We can show these graphs as one graph like this.
postgr3 socst, by(female) outcome(1) y title("readcat=1") ///
legend(order(1 "Male" 2 "Female)) saving(g1)
Variables left asis: socst _Ifemale_1 _IfemXsocst_1
Holding science constant at 51.85
<graph omitted to save space>
postgr3 socst, by(female) outcome(2) ytitle("readcat=2") ///
legend(order(1 "Male" 2 "Female)) saving(g2)
Variables left asis: socst _Ifemale_1 _IfemXsocst_1
Holding science constant at 51.85
<graph omitted to save space>
postgr3 socst, by(female) outcome(2) ytitle("readcat=3") ///
legend(order(1 "Male" 2 "Female)) saving(g3)
Variables left asis: socst _Ifemale_1 _IfemXsocst_1
Holding science constant at 51.85
<graph omitted to save space>
We can then use graph using to show all 3 graphs together.
graph combine g1.gph g2.gph g3.gph
We would use a similar strategy if we had used mlogit.
The use of postgr3 is also possible for an estimation command like quantile regression. Below we run qreg predicting the median reading score.
xi3: qreg read i.ses*i.female science
i.ses _Ises_1-3 (naturally coded; _Ises_1 omitted)
i.female _Ifemale_0-1 (naturally coded; _Ifemale_0 omitted)
i.ses*i.female _IsesXfem_#_# (coded as above)
Iteration 1: WLS sum of weighted deviations = 1256.0231
Iteration 1: sum of abs. weighted deviations = 1253.2
Iteration 2: sum of abs. weighted deviations = 1253.2
Iteration 3: sum of abs. weighted deviations = 1251.6
Iteration 4: sum of abs. weighted deviations = 1246.8
note: alternate solutions exist
Iteration 5: sum of abs. weighted deviations = 1246
Iteration 6: sum of abs. weighted deviations = 1246
Iteration 7: sum of abs. weighted deviations = 1246
Median regression Number of obs = 200
Raw sum of deviations 1684 (about 50)
Min sum of deviations 1246 Pseudo R2 = 0.2601
------------------------------------------------------------------------------
read | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
_Ises_2 | -1.6 4.074188 -0.39 0.695 -9.63565 6.435649
_Ises_3 | 1.6 4.329626 0.37 0.712 -6.939458 10.13946
_Ifemale_1 | -1.8 4.295426 -0.42 0.676 -10.272 6.672005
_IsesXfe~2_1 | 1.8 5.128867 0.35 0.726 -8.315826 11.91583
_IsesXfe~3_1 | 1.8 5.572955 0.32 0.747 -9.191716 12.79172
science | .6 .1008242 5.95 0.000 .4011412 .7988588
_cons | 21.8 6.08162 3.58 0.000 9.805028 33.79497
------------------------------------------------------------------------------
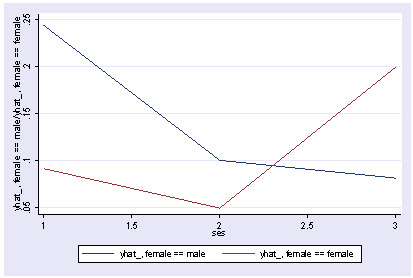
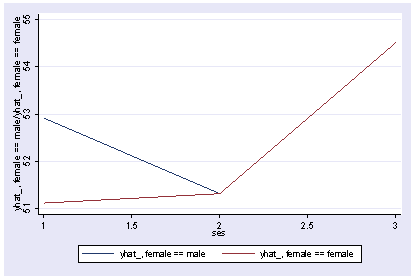
We can show the predicted medians by ses and female as shown below.
postgr3 ses, by(female) Variables left asis: _Ises_2 _Ises_3 _Ifemale_1 _IsesXfem_2_1 _IsesXfem_3_1 Holding science constant at 51.85