_Change_me_to_your_model | Stata Data Analysis Examples

Examples of _your_model

Example 1.

Example 2.

Example 3.

Description of the Data

_Describe_your_data_in_this_section, in Stata, all the data sets should be read in from the internet by using

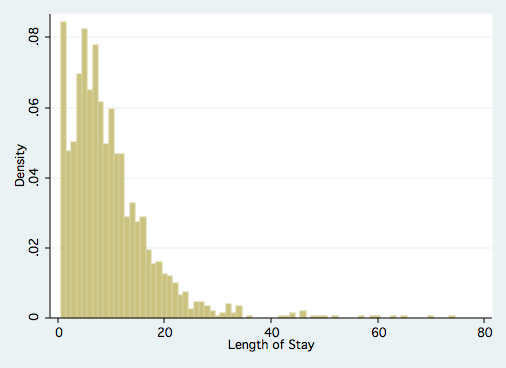
Let’s look at the data.

use https://stats.idre.ucla.edu/stat/stata/notes/hsb2, clear

summarize stay

    Variable |       Obs        Mean    Std. Dev.       Min        Max
-------------+--------------------------------------------------------
        stay |      1493    9.728734    8.132908          1         74

histogram stay, discrete

Some Strategies You Might Be Tempted To Try

Before we show how you can analyze these data with a zero-truncated negative binomial analysis, let’s consider some other methods that you might use.

Enter your words here.
Here is another point of interest.

Stata Zero-Truncated Negative Binomial Analysis

ztnb stay age hmo died

Fitting Zero-truncated poisson model:

(output omitted)

Sample Write-Up of the Analysis

Before we begin the sample write-up we need to get the output into a form more acceptable for publication. In order to go back to the non-exponentiated version of the coefficients we will quietly rerun the ztnb command. The estout command (search estout by Ben Jann of ETH Zurich), will get us close to what we want.

quietly ztnb

estout, cells(b(star fmt(%8.2f)) se(par fmt(%8.2f))) stats(ll chi2, fmt(%8.2f))

        b/se
stay    
age     -0.02
        (0.01)
hmo     -0.15*
        (0.06)
died    -0.22***
        (0.05)
_cons   2.41***
        (0.08)
lnalpha 
_cons   -0.57***
        (0.07)
ll      -4755.28
chi2    25.29

With a little bit of manual editing we can produce an acceptable table of the output. I also manually added the likelihood ratio test for alpha from the non-robust ztnb.

model        
stay             
age               -0.02
                  (0.01)
hmo               -0.15*
                  (0.06)
died              -0.22***
                  (0.05)
constant           2.41***
                  (0.07) 

likelihood ratio
   test for
   alpha        4307.04
log psuedo-
   likelihood  -6908.80
chi-squared       25.29

legend: coefficient/(standard error)  *** p<0.001

The zero-truncated negative binomial regression model predicting length of hospital stay from age, hmo membership and death during the hospital stay was statistically significant (chi-squared = 25.29, df = 3, p<.001). The likelihood ratio test for alpha, the over dispersion parameter, was significant (chi-squared = 4307.04, df = 1, p<.001) indicating that the zero-truncated negative binomial model is preferred over a zero-truncated poisson model. The predictors hmo and died were each statically significant. The effect of age was not significant at the .05 level.

For these data the expected log count for those enrolled in an hmo was -0.15 that of those not so enrolled. This amounts to a difference of about 1.25 days. Patients who died during the hospital stay had an expected log count difference of -0.22 or almost two days.

Cautions, Flies in the Ointment

It is not recommended that zero-truncated negative binomial models be applied to small samples. What constitutes a small sample does not to seem to be clearly defined in the literature.