Version info: Code for this page was tested in Stata 12.
Exact logistic regression is used to model binary outcome variables in which the log odds of the outcome is modeled as a linear combination of the predictor variables. It is used when the sample size is too small for a regular logistic regression (which uses the standard maximum-likelihood-based estimator) and/or when some of the cells formed by the outcome and categorical predictor variable have no observations. The estimates given by exact logistic regression do not depend on asymptotic results.
Please note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and checking, verification of assumptions, model diagnostics or potential follow-up analyses.
Example of exact logistic regression
Suppose that we are interested in the factors that influence whether or not a high school senior is admitted into a very competitive engineering school. The outcome variable is binary (0/1): admit or not admit. The predictor variables of interest include student gender and whether or not the student took Advanced Placement calculus in high school. Because the response variable is binary, we need to use a model that handles 0/1 outcome variables correctly. Also, because of the number of students involved is small, we will need a procedure that can perform the estimation with a small sample size.
Description of the data
The data for this exact logistic data analysis include the number of students admitted, the total number of applicants broken down by gender (the variable female), and whether or not they had taken AP calculus (the variable apcalc). Since the dataset is so small, we will read it in directly.
clear
input female apcalc admit num
0 0 0 7
0 0 1 1
0 1 0 3
0 1 1 7
1 0 0 5
1 0 1 1
1 1 0 0
1 1 1 6
end
Let’s look at some frequency tables. We will specify the variable num as the frequency weight.
tabulate female apcalc [fw=num] | apcalc female | 0 1 | Total -----------+----------------------+---------- 0 | 8 10 | 18 1 | 6 6 | 12 -----------+----------------------+---------- Total | 14 16 | 30 tabulate female admit [fw=num] | admit female | 0 1 | Total -----------+----------------------+---------- 0 | 10 8 | 18 1 | 5 7 | 12 -----------+----------------------+---------- Total | 15 15 | 30 tabulate apcalc admit [fw=num] | admit apcalc | 0 1 | Total -----------+----------------------+---------- 0 | 12 2 | 14 1 | 3 13 | 16 -----------+----------------------+---------- Total | 15 15 | 30table female apcalc admit, content(sum num) ------------------------------------ | admit and apcalc | ---- 0 --- ---- 1 --- female | 0 1 0 1 ----------+------------------------- 0 | 7 3 1 7 1 | 5 0 1 6 ------------------------------------
The tables reveal that 30 students applied for the Engineering program. Of those, 15 were admitted and 15 were denied admission. There were 18 male and 12 female applicants. Sixteen of the applicants had taken AP calculus and 14 had not. Note that all of the females who took AP calculus were admitted, versus only about half the males.
Analysis methods you might consider
Below is a list of some analysis methods you may have encountered. Some of the methods listed are quite reasonable, while others have either fallen out of favor or have limitations.
- Exact logistic regression – This technique is appropriate because the outcome variable is binary, the sample size is small, and some cells are empty.
- Regular logistic regression – Due to the small sample size and the presence of cells with no subjects, regular logistic regression is not advisable, and it might not even be estimable.
- Two-way contingency tables – You may need to use the exact option to get the Fisher’s exact test due to small expected values.
Exact logistic regression
Let’s run the exact logistic analysis using the exlogistic command. We will use the coef option to have the results displayed as logistic regression coefficients (in the log odds metric), rather than the default of odds ratios. As before, we will use num as the frequency weight.
exlogistic admit female apcalc [fw=num], coef
Enumerating sample-space combinations:
observation 1: enumerations = 2
observation 2: enumerations = 4
observation 3: enumerations = 16
observation 4: enumerations = 56
observation 5: enumerations = 282
observation 6: enumerations = 536
observation 7: enumerations = 123
Exact logistic regression Number of obs = 30
Model score = 13.81227
Pr >= score = 0.0005
---------------------------------------------------------------------------
admit | Coef. Suff. 2*Pr(Suff.) [95% Conf. Interval]
-------------+-------------------------------------------------------------
female | 1.360521 7 0.4557 -1.128988 5.367999
apcalc | 3.3387 13 0.0006 1.10166 7.265928
---------------------------------------------------------------------------
- The first part of the output is the log, which shows how many records are generated as each observation is processed. For example, for observation 6 there are 536 unique combinations of the joint distribution for female and apcalc conditioned on the total number of cases. Note that the log lists only seven observations. This is because we input only eight lines of data, and one of those has a count (num) of 0. We use num as a frequency weight to expand the number of observations to 30.
- On the right side of the header information, we see that 30 observations were used in this analysis. We can also see that the overall model is statistically significant. The test of the overall model is a chi-square score, which is why it is called "model score".
- In the table we see the coefficients, the sufficient statistic, the probability, labeled 2*Pr(Suff.), and the 95% confidence interval for the coefficient. The sufficient statistics are single-parameter tests of the null hypothesis that the coefficient equals 0 versus a two-sided alternative. The p-values and confidence intervals are computed from the exact conditional distributions. Note that unlike the estimates given in a regular logistic regression, which would be calculated simultaneously, the estimate of each independent variable is calculated separately with all of the other independent variables conditioned out.
- The variable female is not statistically significant, but the variable apcalc is. For every one unit change in apcalc, the expected log odds of admission (admit) increases by 3.34. The intercept is not included in the output because its sufficient statistic was conditioned out when creating the joint distribution of female and apcalc.
We can issue the exlogistic command without the coef option to see the results displayed as odds ratios.
exlogistic
Exact logistic regression Number of obs = 30
Model score = 13.81227
Pr >= score = 0.0005
---------------------------------------------------------------------------
admit | Odds Ratio Suff. 2*Pr(Suff.) [95% Conf. Interval]
-------------+-------------------------------------------------------------
female | 3.898225 7 0.4557 .3233604 214.4334
apcalc | 28.18247 13 0.0006 3.009156 1430.713
---------------------------------------------------------------------------
The odds for an applicant who had taken AP calculus was about 28.2 times greater than for one who had not taken the course.
We can also obtain the standard errors of the odds ratios using the estat se command.
estat se
-------------------------------------
admit | Odds Ratio Std. Err.
-------------+-----------------------
female | 3.898225 4.560112
apcalc | 28.18247 31.70723
-------------------------------------
You can use the test(score) or test(prob) option to have either the score test or probabilities test displayed. Below we show the probabilities test.
exlogistic, coef test(prob)
Exact logistic regression Number of obs = 30
Model prob. = .0000632
Pr <= prob. = 0.0005
---------------------------------------------------------------------------
admit | Coef. Prob. Pr<=Prob. [95% Conf. Interval]
-------------+-------------------------------------------------------------
female | 1.360521 .1925039 0.3401 -1.128988 5.367999
apcalc | 3.3387 .0002831 0.0003 1.10166 7.265928
---------------------------------------------------------------------------
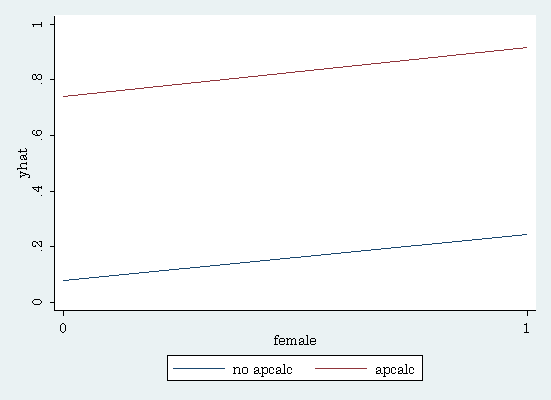
We can also graph the predicted probabilities. To do this, we will create a new variable called yhat and set it equal to missing. Then we will replace the missing values for each combination of female and apcalc. Finally, we will use the twoway command to create the graph.
gen yhat = . estat predict, at(female=1 apcalc=1) replace yhat= r(pred) if female ==1 & apcalc==1 estat predict, at(female=0 apcalc=1) replace yhat= r(pred) if female ==0 & apcalc==1 estat predict, at(female=1 apcalc=0) replace yhat= r(pred) if female ==1 & apcalc==0 estat predict, at(female=0 apcalc=0) replace yhat= r(pred) if female ==0 & apcalc==0 twoway (line yhat female if apcalc==0) (line yhat female if apcalc==1), /// xlabel(0 1) ylabel(0(.2)1, nogrid) legend(label(1 "no apcalc") label(2 "apcalc"))
Things to consider
- Firth logit may be helpful if you have separation in your data. You can use search to download the user-written firthlogit command (search firthlogit) (see How can I use the search command to search for programs and get additional help? for more information about using search).
- Exact logistic regression is an alternative to conditional logistic regression if you have stratification, since both condition on the number of positive outcomes within each stratum. The estimates from these two analyses will be different because clogit conditions only on the intercept term, while exlogistic conditions on the sufficient statistics of the other regression parameters as well as the intercept term.
See also
- Stata help for exlogistic
- Stata manual entry for exlogistic, see [R] exlogistic
References
- Collett, D. Modeling Binary Data, Second Edition. Boca Raton: Chapman and Hall.
- Cox, D. R. and Snell, E. J. (1989). Analysis of Binary Data, Second Edition. Boca Raton: Chapman and Hall.
- Hirji, K. F. (2005). Exact Analysis of Discrete Data. Boca Raton: Chapman and Hall.