Version info: Code for this page was tested in Stata 17.
Zero-inflated negative binomial regression is for modeling count variables with excessive zeros and it is usually for over-dispersed count outcome variables. Furthermore, theory suggests that the excess zeros are generated by a separate process from the count values and that the excess zeros can be modeled independently.
Please note: The purpose of this page is to show how to use various data analysis commands. It does not cover all aspects of the research process which researchers are expected to do. In particular, it does not cover data cleaning and checking, verification of assumptions, model diagnostics or potential follow-up analyses.
Examples of zero-inflated negative binomial regression
Example 1.
School administrators study the attendance behavior of high school juniors at two schools. Predictors of the number of days of absence include gender of the student and standardized test scores in math and language arts.
Example 2.
The state wildlife biologists want to model how many fish are being caught by fishermen at a state park. Visitors are asked how long they stayed, how many people were in the group, were there children in the group and how many fish were caught. Some visitors do not fish, but there is no data on whether a person fished or not. Some visitors who did fish did not catch any fish so there are excess zeros in the data because of the people that did not fish.
Description of the data
Let’s pursue Example 2 from above. The data set used in this example is from Stata.
We have data on 250 groups that went to a park. Each group was questioned before leaving the park about how many fish they caught (count), how many children were in the group (child), how many people were in the group (persons), and whether or not they brought a camper to the park (camper). The outcome variable of interest will be the number of fish caught. Even though the question about the number of fish caught was asked to everyone, it does not mean that everyone went fishing. What would be the reason for someone to report a zero count? Was it because this person was unlucky and didn’t catch any fish, or was it because this person didn’t go fishing at all? If a person didn’t go fishing, the outcome would be always zero. Otherwise, if a person went to fishing, the count could be zero or non-zero. So we can see that there seemed to be two processes that would generate zero counts: unlucky in fishing or didn’t go fishing.
Let’s first look at the data. We will start with reading in the data and the descriptive statistics and plots. This helps us understand the data and give us some hint on how we should model the data.
webuse fish summarize count child persons camperVariable | Obs Mean Std. Dev. Min Max -------------+-------------------------------------------------------- count | 250 3.296 11.63503 0 149 child | 250 .684 .8503153 0 3 persons | 250 2.528 1.11273 1 4 camper | 250 .588 .4931824 0 1 histogram count, discrete freqtab1 child persons camper -> tabulation of child child | Freq. Percent Cum. ------------+----------------------------------- 0 | 132 52.80 52.80 1 | 75 30.00 82.80 2 | 33 13.20 96.00 3 | 10 4.00 100.00 ------------+----------------------------------- Total | 250 100.00 -> tabulation of persons persons | Freq. Percent Cum. ------------+----------------------------------- 1 | 57 22.80 22.80 2 | 70 28.00 50.80 3 | 57 22.80 73.60 4 | 66 26.40 100.00 ------------+----------------------------------- Total | 250 100.00 -> tabulation of camper camper | Freq. Percent Cum. ------------+----------------------------------- 0 | 103 41.20 41.20 1 | 147 58.80 100.00 ------------+----------------------------------- Total | 250 100.00
tabstat count, by(camper) stats(mean v n) Summary for variables: count by categories of: camper camper | mean variance N ---------+------------------------------ 0 | 1.524272 21.05578 103 1 | 4.537415 212.401 147 ---------+------------------------------ Total | 3.296 135.3739 250 ----------------------------------------
We can see from the table of descriptive statistics above that the variance of the outcome variable is quite large relative to the means. This might be an indication of over-dispersion.
Analysis methods you might consider
Before we show how you can analyze this with a zero-inflated negative binomial analysis, let’s consider some other methods that you might use.
- OLS Regression – You could try to analyze these data using OLS regression. However, count data are highly non-normal and are not well estimated by OLS regression.
- Zero-inflated Poisson Regression – Zero-inflated Poisson regression does better when the data are not over-dispersed, i.e. when variance is not much larger than the mean.
- Ordinary Count Models – Poisson or negative binomial models might be more appropriate if there are not excess zeros.
Zero-inflated negative binomial regression
A zero-inflated model assumes that zero outcome is due to two different processes. For instance, in the example of fishing presented here, the two processes are that a subject has gone fishing vs. not gone fishing. If not gone fishing, the only outcome possible is zero. If gone fishing, it is then a count process. The two parts of the a zero-inflated model are a binary model, usually a logit model to model which of the two processes the zero outcome is associated with and a count model, in this case, a negative binomial model, to model the count process. The expected count is expressed as a combination of the two processes. Taking the example of fishing again, E(#of fish caught=k) = prob(not gone fishing )*0 + prob(gone fishing)*E(y=k|gone fishing).
Now let’s build up our model. We are going to use the variables child and camper to model the count in the part of negative binomial model and the variable persons in the logit part of the model. The Stata command is shown below. We treat variable camper as a categorical variable by putting a prefix “-i.-” in front of the variable name. This will make the post estimations easier. We have included the zip option, which provides a likelihood ratio test of alpha=0 (basically zinb versus zip).
zinb count child i.camper, inflate(persons) zip
Fitting constant-only model:
Iteration 0: log likelihood = -519.33992
Iteration 1: log likelihood = -471.96077
Iteration 2: log likelihood = -465.38193
Iteration 3: log likelihood = -464.39882
Iteration 4: log likelihood = -463.92704
Iteration 5: log likelihood = -463.79248
Iteration 6: log likelihood = -463.75773
Iteration 7: log likelihood = -463.7518
Iteration 8: log likelihood = -463.75119
Iteration 9: log likelihood = -463.75118
Fitting full model:
Iteration 0: log likelihood = -463.75118 (not concave)
Iteration 1: log likelihood = -440.43162
Iteration 2: log likelihood = -434.96651
Iteration 3: log likelihood = -433.49903
Iteration 4: log likelihood = -432.89949
Iteration 5: log likelihood = -432.89091
Iteration 6: log likelihood = -432.89091
Zero-inflated negative binomial regression Number of obs = 250
Inflation model: logit Nonzero obs = 108
Zero obs = 142
LR chi2(2) = 61.72
Log likelihood = -432.8909 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
count | Coefficient Std. err. z P>|z| [95% conf. interval]
-------------+----------------------------------------------------------------
count |
child | -1.515255 .1955912 -7.75 0.000 -1.898606 -1.131903
1.camper | .8790514 .2692731 3.26 0.001 .3512857 1.406817
_cons | 1.371048 .2561131 5.35 0.000 .8690758 1.873021
-------------+----------------------------------------------------------------
inflate |
persons | -1.666563 .6792833 -2.45 0.014 -2.997934 -.3351922
_cons | 1.603104 .8365065 1.92 0.055 -.036419 3.242626
-------------+----------------------------------------------------------------
/lnalpha | .9853533 .17595 5.60 0.000 .6404975 1.330209
-------------+----------------------------------------------------------------
alpha | 2.678758 .4713275 1.897425 3.781834
------------------------------------------------------------------------------
Likelihood-ratio test of alpha=0: chibar2(01) = 1197.43 Pr>=chibar2 = 0.0000
The output has a few components which are explained below.
- It begins with the iteration log giving the values of the log likelihoods starting with a model that has no predictors and intercept set to zero for the inflated model.
- The last value in the log is the final value of the log likelihood for the full model and is repeated below.
- Next comes the header information. On the right-hand side the number of observations used (316) is given along with the likelihood ratio chi-squared. This compares the full model to a model without count predictors, giving a difference of two degrees of freedom.
- This is followed by the p-value for the chi-square. The model, as a whole, is statistically significant.
- Below the header, you will find the negative binomial regression coefficients for each of the variables along with standard errors, z-scores, p-values and 95% confidence intervals for the coefficients.
- Following these are logit coefficients for predicting excess zeros along with their standard errors, z-scores, p-values and confidence intervals.
- Additionally, there will be an estimate of the natural log of the over dispersion coefficient, alpha, along with the untransformed value. If the alpha coefficient is zero then the model is better estimated using an Poisson regression model.
- Below the various coefficients you will find the results of the zip
option.
- The zip option tests the zero-inflated negative binomial model versus the zero-inflated Poisson model. A significant likelihood ratio test for alpha=0 indicates that the zinb model is preferred to the zip model.
Looking through the results of regression parameters we see the following:
- The predictors child and camper in the part of the negative binomial regression model predicting number of fish caught (count) are both significant predictors.
- The predictor person in the part of the logit model predicting excessive zeros is statistically significant.
- For these data, the expected change in log(count) for a one-unit increase in child is -1.515255 holding other variables constant.
- A camper (camper = 1) has an expected log(count) of 0.879051 higher than that of a non-camper (camper = 0) holding other variables constant.
- The log odds of being an excessive zero would decrease by 1.67 for every additional person in the group. In other words, the more people in the group the less likely that the zero would be due to not gone fishing. Put it plainly, the larger the group the person was in, the more likely that the person went fishing.
- We can see at the bottom of our model that the likelihood ratio test that alpha = 0 is significantly different from zero. This suggests that our data are over-dispersed and that a zero-inflated negative binomial model is more appropriate than a zero-inflated Poisson model.
Now, just to be on the safe side, let’s rerun the zinb command with the robust option in order to obtain robust standard errors for the Poisson regression coefficients.
zinb count child i.camper, inflate(persons) robust
Fitting constant-only model:
Iteration 0: log pseudolikelihood = -519.33992
Iteration 1: log pseudolikelihood = -471.96077
Iteration 2: log pseudolikelihood = -465.38193
Iteration 3: log pseudolikelihood = -464.39882
Iteration 4: log pseudolikelihood = -463.92704
Iteration 5: log pseudolikelihood = -463.79248
Iteration 6: log pseudolikelihood = -463.75773
Iteration 7: log pseudolikelihood = -463.7518
Iteration 8: log pseudolikelihood = -463.75119
Iteration 9: log pseudolikelihood = -463.75118
Fitting full model:
Iteration 0: log pseudolikelihood = -463.75118 (not concave)
Iteration 1: log pseudolikelihood = -440.43162
Iteration 2: log pseudolikelihood = -434.96651
Iteration 3: log pseudolikelihood = -433.49903
Iteration 4: log pseudolikelihood = -432.89949
Iteration 5: log pseudolikelihood = -432.89091
Iteration 6: log pseudolikelihood = -432.89091
Zero-inflated negative binomial regression Number of obs = 250
Nonzero obs = 108
Zero obs = 142
Inflation model = logit Wald chi2(2) = 40.16
Log pseudolikelihood = -432.8909 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
| Robust
count | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
count |
child | -1.515255 .2417504 -6.27 0.000 -1.989077 -1.041432
1.camper | .8790514 .471303 1.87 0.062 -.0446855 1.802788
_cons | 1.371048 .3902521 3.51 0.000 .6061682 2.135928
-------------+----------------------------------------------------------------
inflate |
persons | -1.666563 .4314861 -3.86 0.000 -2.51226 -.8208658
_cons | 1.603104 .6665327 2.41 0.016 .2967236 2.909484
-------------+----------------------------------------------------------------
/lnalpha | .9853533 .2157394 4.57 0.000 .5625119 1.408195
-------------+----------------------------------------------------------------
alpha | 2.678758 .5779135 1.755075 4.088567
------------------------------------------------------------------------------
Using the robust option has resulted in some change in the model chi-square, which is now a Wald chi-square. This statistic is based on log pseudo-likelihoods instead of log-likelihoods. The model is still statistically significant.
The robust standard errors attempt to adjust for heterogeneity in the model.
Now, let’s try to understand the model better by using some of the post estimation commands. First off, we use the predict command with the pr option to get the predicted probability of being “an excessive zero” due to not having gone fishing. We then look the distribution of the predicted probability by the number of persons in the group. We can see that the larger the group, the smaller the probability, meaning the more likely that the person went fishing.
predict p, pr table persons, con(mean p)---------------------- persons | mean(p) ----------+----------- 1 | .4841405 2 | .1505847 3 | .0324023 4 | .0062859 ----------------------
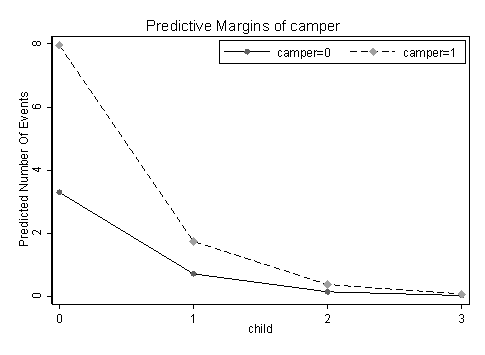
Finally, we will use the margins command to get the predicted number of fish caught, comparing campers with non-campers given different number of children and marginsplot to visualize the information produced by the margins command.
margins camper, at(child=(0(1)3))Predictive margins Number of obs = 250 Model VCE : Robust Expression : Predicted number of events, predict() 1._at : child = 0 2._at : child = 1 3._at : child = 2 4._at : child = 3 ------------------------------------------------------------------------------ | Delta-method | Margin Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- _at#camper | 1 0 | 3.302878 1.294607 2.55 0.011 .7654961 5.840261 1 1 | 7.955358 2.056003 3.87 0.000 3.925667 11.98505 2 0 | .7258149 .3452292 2.10 0.036 .049178 1.402452 2 1 | 1.748208 .3534415 4.95 0.000 1.055475 2.44094 3 0 | .1594994 .1028401 1.55 0.121 -.0420634 .3610623 3 1 | .3841725 .1394934 2.75 0.006 .1107704 .6575747 4 0 | .0350504 .0297846 1.18 0.239 -.0233263 .093427 4 1 | .0844228 .0492046 1.72 0.086 -.0120164 .180862 ------------------------------------------------------------------------------ marginsplot, noci scheme(s1mono) legend(position(1) ring(0))
Notice that by default the margins command fixed the expected predicted probability of being an excessive zero at its mean. For instance, here is an alternative way for producing the same predicted count given camper = 0 /1 and child = 0.
sum pr local mean_pr = r(mean) margins camper, at(child=0) expression(exp(predict(xb))*(1-`mean_pr'))Predictive margins Number of obs = 250 Model VCE : RobustExpression : exp(predict(xb))*(1-.1615949432440102) at : child = 0------------------------------------------------------------------------------ | Delta-method | Margin Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- camper | 0 | 3.302879 1.288955 2.56 0.010 .7765726 5.829184 1 | 7.955358 2.180409 3.65 0.000 3.681835 12.22888 ------------------------------------------------------------------------------
Things to consider
Here are some issues that you may want to consider in the course of your research analysis.
- Question about the over-dispersion parameter is in general a tricky one. A large over-dispersion parameter could be due to a miss-specified model or could be due to a real process with over-dispersion. Adding an over-dispersion problem does not necessarily improve a miss-specified model.
- The zinb model has two parts, a negative binomial count model and the logit model for predicting excess zeros, so you might want to review these Data Analysis Example pages, Negative Binomial Regression and Logit Regression.
- Since zinb has both a count model and a logit model, each of the two models should have good predictors. The two models do not necessarily need to use the same predictors.
- Problems of perfect prediction, separation or partial separation can occur in the logistic part of the zero-inflated model.
- Count data often use exposure variable to indicate the number of times the event could have happened. You can incorporate exposure into your model by using the exposure() option.
- It is not recommended that zero-inflated negative binomial models be applied to small samples. What constitutes a small sample does not seem to be clearly defined in the literature.
- Pseudo-R-squared values differ from OLS R-squareds, please see FAQ: What are pseudo R-squareds? for a discussion on this issue.
- In times past, the Vuong test had been used to test whether a zero-inflated negative binomial model or a negative binomial model (without the zero-inflation) was a better fit for the data. However, this test is no longer considered valid. Please see The Misuse of The Vuong Test For Non-Nested Models to Test for Zero-Inflation by Paul Wilson for further information.
See Also
References
- Cameron, A. Colin and Trivedi, P.K. (2009) Microeconometrics using Stata. College Station, TX: Stata Press.
- Long, J. Scott, & Freese, Jeremy (2006). Regression Models for Categorical Dependent Variables Using Stata (Second Edition). College Station, TX: Stata Press.
- Long, J. Scott (1997). Regression Models for Categorical and Limited Dependent Variables. Thousand Oaks, CA: Sage Publications.
Last updated on October 12, 2011