Table 1.1, page 3.
use chdage.dta, clear
(Hosmer and Lemeshow - from chapter 1)
gen agrp=age
recode agrp 20/29=1 30/34=2 35/39=3 40/44=4 45/49=5 50/54=6 55/59=7 60/69=8
(100 changes made)
list id age agrp chd
id age agrp chd
1. 1 20 1 0
2. 2 23 1 0
3. 3 24 1 0
4. 4 25 1 0
5. 5 25 1 1
6. 6 26 1 0
7. 7 26 1 0
8. 8 28 1 0
9. 9 28 1 0
10. 10 29 1 0
11. 11 30 2 0
12. 12 30 2 0
13. 13 30 2 0
14. 14 30 2 0
15. 15 30 2 0
16. 16 30 2 1
17. 17 32 2 0
18. 18 32 2 0
19. 19 33 2 0
20. 20 33 2 0
21. 21 34 2 0
22. 22 34 2 0
23. 23 34 2 1
24. 24 34 2 0
25. 25 34 2 0
26. 26 35 3 0
27. 27 35 3 0
28. 28 36 3 0
29. 29 36 3 1
30. 30 36 3 0
31. 31 37 3 0
32. 32 37 3 1
33. 33 37 3 0
34. 34 38 3 0
35. 35 38 3 0
36. 36 39 3 0
37. 37 39 3 1
38. 38 40 4 0
39. 39 40 4 1
40. 40 41 4 0
41. 41 41 4 0
42. 42 42 4 0
43. 43 42 4 0
44. 44 42 4 0
45. 45 42 4 1
46. 46 43 4 0
47. 47 43 4 0
48. 48 43 4 1
49. 49 44 4 0
50. 50 44 4 0
51. 51 44 4 1
52. 52 44 4 1
53. 53 45 5 0
54. 54 45 5 1
55. 55 46 5 0
56. 56 46 5 1
57. 57 47 5 0
58. 58 47 5 0
59. 59 47 5 1
60. 60 48 5 0
61. 61 48 5 1
62. 62 48 5 1
63. 63 49 5 0
64. 64 49 5 0
65. 65 49 5 1
66. 66 50 6 0
67. 67 50 6 1
68. 68 51 6 0
69. 69 52 6 0
70. 70 52 6 1
71. 71 53 6 1
72. 72 53 6 1
73. 73 54 6 1
74. 74 55 7 0
75. 75 55 7 1
76. 76 55 7 1
77. 77 56 7 1
78. 78 56 7 1
79. 79 56 7 1
80. 80 57 7 0
81. 81 57 7 0
82. 82 57 7 1
83. 83 57 7 1
84. 84 57 7 1
85. 85 57 7 1
86. 86 58 7 0
87. 87 58 7 1
88. 88 58 7 1
89. 89 59 7 1
90. 90 59 7 1
91. 91 60 8 0
92. 92 60 8 1
93. 93 61 8 1
94. 94 62 8 1
95. 95 62 8 1
96. 96 63 8 1
97. 97 64 8 0
98. 98 64 8 1
99. 99 65 8 1
100. 100 69 8 1
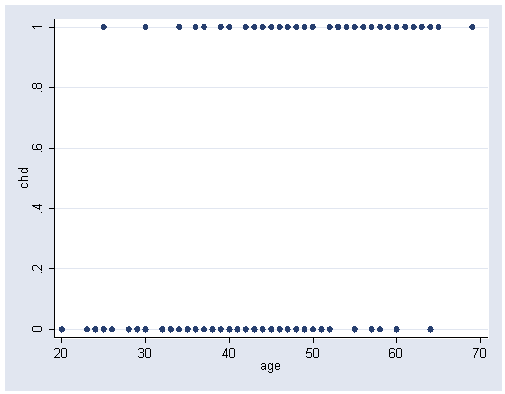
Figure 1.1, page 4.
graph twoway scatter chd age, xlabel(20(10)70) ylabel(0(.2)1)
Table 1.2, page 4.
sort agrp
collapse (count) tot=chd (sum) present=chd, by(agrp)
gen prop = present / tot
gen absent = tot - present
gen count = present + absent
list agrp count absent present prop
agrp count absent present prop
1. 1 10 9 1 .1
2. 2 15 13 2 .1333333
3. 3 12 9 3 .25
4. 4 15 10 5 .3333333
5. 5 13 7 6 .4615385
6. 6 8 3 5 .625
7. 7 17 4 13 .7647059
8. 8 10 2 8 .8
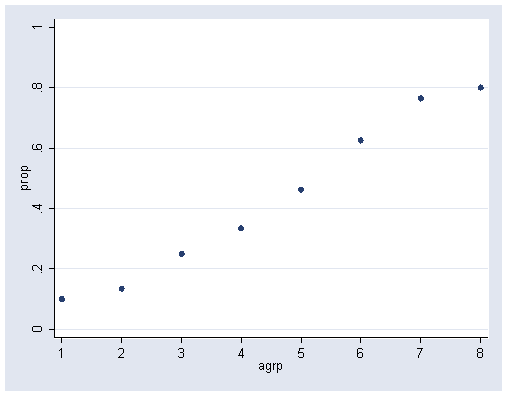
Figure 1.2, page 5.
graph twoway scatter prop agrp, ylabel(0(.2)1) xlabel(1(1)8)
Table 1.3, page 10.
use chdage.dta, clear
(Hosmer and Lemeshow - from chapter 1)
logistic chd age, coef
Logit estimates Number of obs = 100
LR chi2(1) = 29.31
Prob > chi2 = 0.0000
Log likelihood = -53.676546 Pseudo R2 = 0.2145
------------------------------------------------------------------------------
chd | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | .1109211 .0240598 4.61 0.000 .0637647 .1580776
_cons | -5.309453 1.133655 -4.68 0.000 -7.531376 -3.087531
------------------------------------------------------------------------------
or you could use
logit chd age
Iteration 0: log likelihood = -68.331491
Iteration 1: log likelihood = -54.170558
Iteration 2: log likelihood = -53.681645
Iteration 3: log likelihood = -53.676547
Iteration 4: log likelihood = -53.676546
Logit estimates Number of obs = 100
LR chi2(1) = 29.31
Prob > chi2 = 0.0000
Log likelihood = -53.676546 Pseudo R2 = 0.2145
------------------------------------------------------------------------------
chd | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
age | .1109211 .0240598 4.61 0.000 .0637647 .1580776
_cons | -5.309453 1.133655 -4.68 0.000 -7.531376 -3.087531
------------------------------------------------------------------------------
Table 1.4, page 20.
* Stata 8 code.
vce
* Stata 9 code and output.
estat vce
Covariance matrix of coefficients of logit model
e(V) | age _cons
-------------+------------------------
age | .00057888
_cons | -.02667702 1.2851728