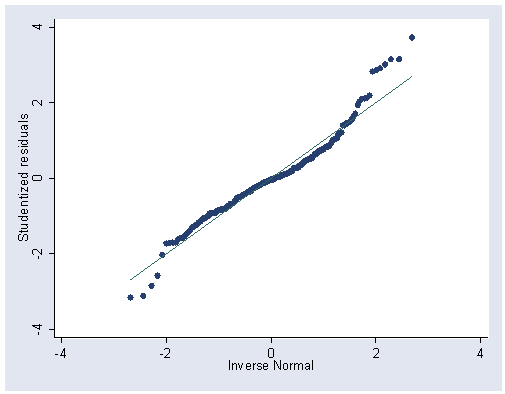
Figure 12.1, figure 12.2 and table 12.1, page 297-299 on data file ornstein. We skip the section on confidence envelopes. We only have the usual normal quantile plots without the confidence envelopes.
use https://stats.idre.ucla.edu/stat/stata/examples/ara/ornstein, clear
tab sector, gen(sect) /*generate dummy variables*/
(Output omitted here)
tab nation, gen(nat)/*generate dummy variables*/
(Output omitted here)
gen asset1=sqrt(assets)/*generate a new regressor*/
regress intrlcks asset1 nat2-nat4 sect1-sect5 sect7-sect10
Source | SS df MS Number of obs = 248
---------+------------------------------ F( 13, 234) = 34.11
Model | 41816.5529 13 3216.65791 Prob > F = 0.0000
Residual | 22069.8342 234 94.3155309 R-squared = 0.6545
---------+------------------------------ Adj R-squared = 0.6354
Total | 63886.3871 247 258.64934 Root MSE = 9.7116
------------------------------------------------------------------------------
intrlcks | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
asset1 | .2517892 .0185222 13.594 0.000 .2152976 .2882808
nat2 | -1.158915 2.664005 -0.435 0.664 -6.407413 4.089584
nat3 | -4.444009 2.649276 -1.677 0.095 -9.66349 .7754719
nat4 | -8.089053 1.481003 -5.462 0.000 -11.00686 -5.171248
sect1 | -1.199539 2.04038 -0.588 0.557 -5.219402 2.820323
sect2 | -14.37594 5.576992 -2.578 0.011 -25.36347 -3.388413
sect3 | -5.12563 4.698778 -1.091 0.276 -14.38294 4.131683
sect4 | -5.698507 2.925712 -1.948 0.053 -11.46261 .065596
sect5 | -2.430237 4.014109 -0.605 0.545 -10.33865 5.478175
sect7 | -.8668517 2.63433 -0.329 0.742 -6.056886 4.323183
sect8 | .3422809 2.012105 0.170 0.865 -3.621874 4.306436
sect9 | -.3810376 2.819743 -0.135 0.893 -5.936365 5.17429
sect10 | 5.151303 2.682082 1.921 0.056 -.1328104 10.43542
_cons | 4.190453 1.846039 2.270 0.024 .5534732 7.827433
------------------------------------------------------------------------------
predict student, rstudent
qnorm student
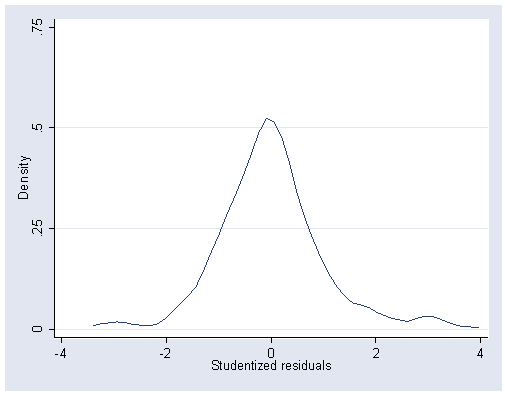
Figure 12.1 (b) on page 297.
kdensity student, ylabel(0(.25).75)
gen inlck=sqrt(intrlcks+1)
regress inlck asset1 nat2-nat4 sect1-sect5 sect7-sect10
Source | SS df MS Number of obs = 248
---------+------------------------------ F( 13, 234) = 24.89
Model | 477.296638 13 36.715126 Prob > F = 0.0000
Residual | 345.199855 234 1.47521306 R-squared = 0.5803
---------+------------------------------ Adj R-squared = 0.5570
Total | 822.496493 247 3.32994531 Root MSE = 1.2146
------------------------------------------------------------------------------
inlck | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
asset1 | .0260108 .0023165 11.229 0.000 .021447 .0305747
nat2 | -.1139589 .3331737 -0.342 0.733 -.7703624 .5424445
nat3 | -.5266014 .3313317 -1.589 0.113 -1.179376 .1261729
nat4 | -1.105112 .1852217 -5.966 0.000 -1.470027 -.740197
sect1 | -.0567192 .2551801 -0.222 0.824 -.5594633 .4460249
sect2 | -2.250759 .6974864 -3.227 0.001 -3.624915 -.8766039
sect3 | -.7399749 .5876526 -1.259 0.209 -1.897741 .417791
sect4 | -.0880438 .3659042 -0.241 0.810 -.8089313 .6328437
sect5 | -.2453168 .5020245 -0.489 0.626 -1.234382 .7437487
sect7 | .1479077 .3294624 0.449 0.654 -.5011839 .7969993
sect8 | .3562041 .2516439 1.416 0.158 -.139573 .8519811
sect9 | .3540146 .3526512 1.004 0.316 -.3407624 1.048792
sect10 | .7860363 .3354345 2.343 0.020 .1251788 1.446894
_cons | 2.329308 .2308748 10.089 0.000 1.874449 2.784167
------------------------------------------------------------------------------
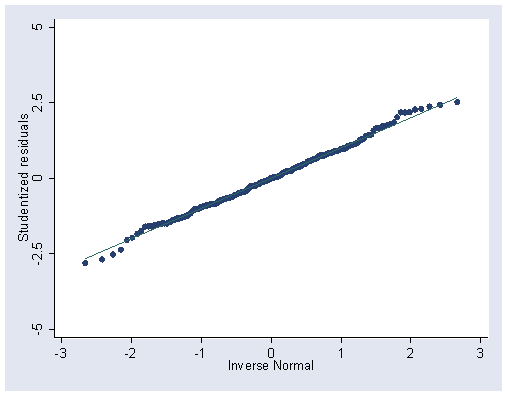
predict student1, rstudent
qnorm student1, ylabel(-5(2.5)5) xlabel(-3(1)3)
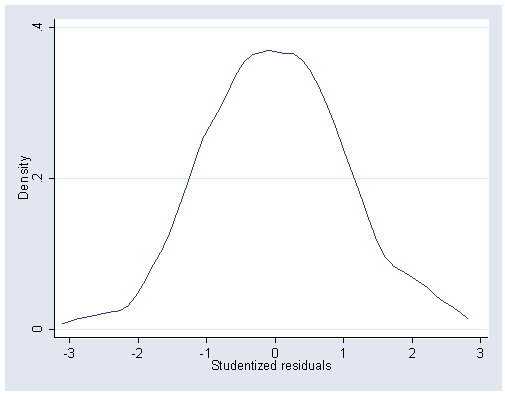
Figure 12.2 (b), page 299.
kdensity student1, xlabel(-3(1)3) ylabel(0 .2 .4)
Remark: Combining the results from the two regression procedures, we get the result for Table 12.1, page 298.
Figure 12.3 (a) on page 303 on data file ornstein.
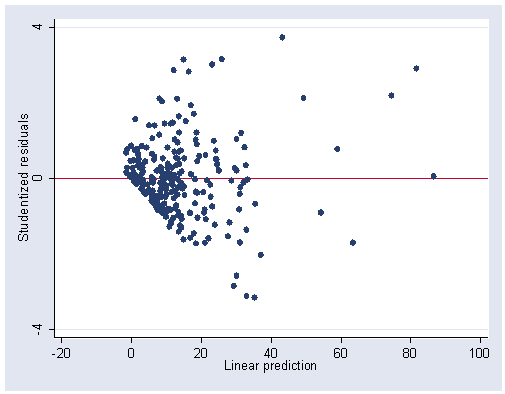
regress intrlcks asset1 nat2-nat4 sect1-sect5 sect7-sect10 (Output omitted here.) predict fitted1, xb /*use student residuals from the first regression in previous section*/ graph twoway scatter student fitted1, yline(0) ylabel(-4 0 4) xlabel(-20(20)100)
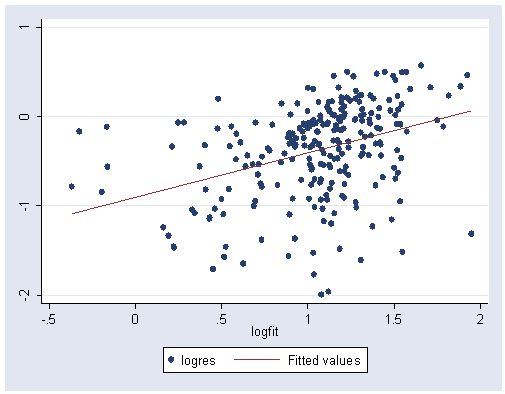
Figure 12.3 (b) on page 303.
gen logfit=log10(2+fitted1) gen logres = log10(abs(student)) graph twoway (scatter logres logfit)(lfit logres logfit), ylabel(-2(1)1)
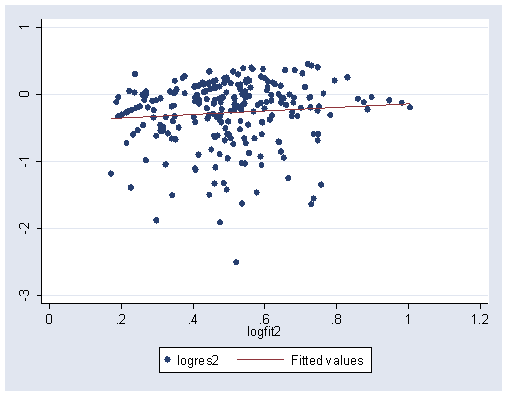
regress inlck asset1 nat2-nat4 sect1-sect5 sect7-sect10 (Output omitted here) predict fitted2, xb gen logfit2=log10(fitted2) gen logres2=log10(abs(student1)) graph twoway (scatter logres2 logfit2)(lfit logres2 logfit2), ylabel(-3(1)1) xlabel(0(.2)1.2)
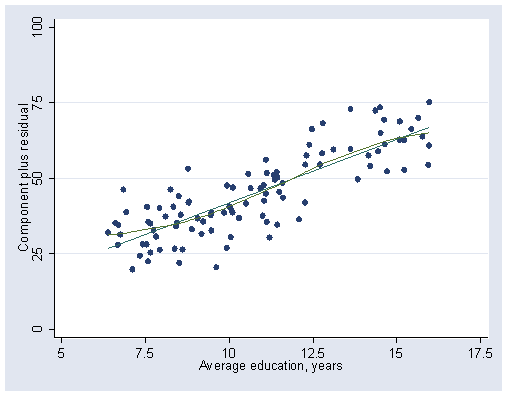
Figure 12.6 (a), (b) and (c) on page 312. Notice that procedure cprplot gives partial residual plot and we use the lowess option to get the nonparametric-regression smoothing shown in the book.
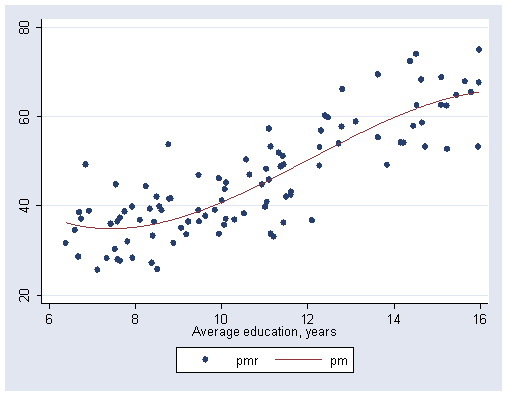
use https://stats.idre.ucla.edu/stat/stata/examples/ara/prestige, clear (From Fox, Applied Regression Analysis. Use 'notes' command for source of data) regress prestige percwomn educat income (Output omitted here.) cprplot educat, lowess ylabel(0(25)100) xlabel(5(2.5)17.5)
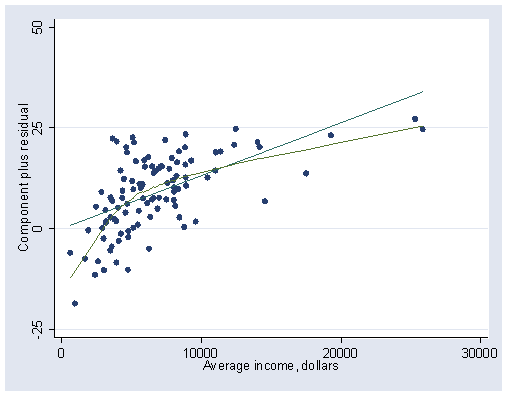
cprplot income, lowess ylabel(-25(25)50) xlabel(0(10000)30000)
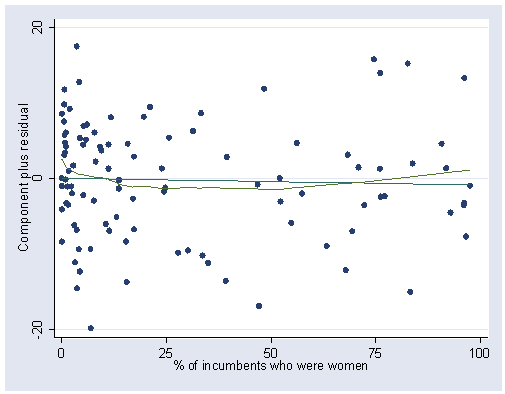
cprplot percwomn, lowess ylabel(-20 0 20) xlabel(0(25)100)
Formula in the middle of page 313 still using the data file prestige.
gen loginc=log10(income)/log10(2)
gen edu2=educat*educat
gen edu3=edu2*educat
gen w2=percwomn*percwomn
regress prestige loginc percwomn w2 educat edu2 edu3
Source | SS df MS Number of obs = 102
---------+------------------------------ F( 6, 95) = 94.46
Model | 25603.6492 6 4267.27487 Prob > F = 0.0000
Residual | 4291.77689 95 45.1765988 R-squared = 0.8564
---------+------------------------------ Adj R-squared = 0.8474
Total | 29895.4261 101 295.994318 Root MSE = 6.7214
------------------------------------------------------------------------------
prestige | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
loginc | 8.783331 1.272748 6.901 0.000 6.256608 11.31005
percwomn | -.179323 .085088 -2.108 0.038 -.3482439 -.010402
w2 | .0025001 .0009245 2.704 0.008 .0006648 .0043354
educat | -29.92002 15.25152 -1.962 0.053 -60.19811 .3580668
edu2 | 2.915935 1.414413 2.062 0.042 .1079704 5.723901
edu3 | -.0806755 .0422082 -1.911 0.059 -.1644694 .0031185
_cons | 20.83852 56.89955 0.366 0.715 -92.12136 133.7984
------------------------------------------------------------------------------
predict res2, r
summarize income percwomn /*get mean for income and percwomn*/
Variable | Obs Mean Std. Dev. Min Max
---------+-----------------------------------------------------
income | 102 6797.902 4245.922 611 25879
percwomn | 102 28.97902 31.72493 0 97.51
gen pm=20.8+8.78*log10(6797.902)/log10(2)-0.179*28.979+0.0025*28.979*28.979-29.9*educat+2.91*edu2-.0807*edu3
gen pmr=res2 + pm
graph twoway scatter pmr pm educat, connect(i l) sort msymbol(O i O)
Table 12.2 on page 319.
use https://stats.idre.ucla.edu/stat/stata/examples/ara/vocab, clear (From Fox, Applied Regression Analysis. Use 'notes' command for source of data) regress vocab educ Source | SS df MS Number of obs = 968 ---------+------------------------------ F( 1, 966) = 318.92 Model | 1175.11129 1 1175.11129 Prob > F = 0.0000 Residual | 3559.41351 966 3.68469307 R-squared = 0.2482 ---------+------------------------------ Adj R-squared = 0.2474 Total | 4734.52479 967 4.89609596 Root MSE = 1.9196 (Further output omitted.) xi: regress vocab i.educ i.educ Ieduc_0-20 (naturally coded; Ieduc_0 omitted) Source | SS df MS Number of obs = 968 ---------+------------------------------ F( 19, 948) = 18.13 Model | 1261.69388 19 66.4049413 Prob > F = 0.0000 Residual | 3472.83091 948 3.66332374 R-squared = 0.2665 ---------+------------------------------ Adj R-squared = 0.2518 Total | 4734.52479 967 4.89609596 Root MSE = 1.914 (Further output omitted)
With the results from these two regressions, we can calculate the nonlinear effect as follows.
display 1261.69399-1175.11129/*Sum of Squares for nonlinear effect*/ 86.5827 display (86.57/18)/(3472.8/948)/*F-value*/ 1.3128753 display fprob(18, 948, 1.31)/*p-value*/ .17255134
The first part is on Box-Cox transformation on the dependent variable using the data file ornstein, calculation on page 323 and 324.
use https://stats.idre.ucla.edu/stat/stata/examples/ara/ornstein, clear
gen dep=intrlcks+1 /*This is the dependent variable used through the example.*/
gen asset1=sqrt(assets) /*regressor obtained from independent variable assets. */
gen logy=ln(dep) /*To get geometric mean suggested in the footnote.*/
egen c1=mean(logy) /*Contiue on geometric mean*/
gen c=exp(c1)
display c /* showing geometric mean of the dependent variable*/
8.2501268
gen cv=dep*(ln(dep/c)-1) /*generate constructed variable*/
xi: regress dep asset1 i.nation i.sector cv
i.nation Inatio_1-4 (Inatio_1 for nation==CAN omitted)
i.sector Isect_1-10 (Isect_1 for sector==AGR omitted)
Source | SS df MS Number of obs = 248
---------+------------------------------ F( 14, 233) = 103.67
Model | 55048.7339 14 3932.05242 Prob > F = 0.0000
Residual | 8837.65321 233 37.9298421 R-squared = 0.8617
---------+------------------------------ Adj R-squared = 0.8534
Total | 63886.3871 247 258.64934 Root MSE = 6.1587
------------------------------------------------------------------------------
dep | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
asset1 | .0699101 .0152576 4.582 0.000 .0398497 .0999705
Inatio_2 | -.1373967 1.690291 -0.081 0.935 -3.467603 3.19281.....(continued)
cv | .5850363 .0313226 18.678 0.000 .5233246 .646748
_cons | 11.38911 1.132516 10.056 0.000 9.15783 13.62039
------------------------------------------------------------------------------
test cv=0
( 1) cv = 0.0
F( 1, 233) = 348.86
Prob > F = 0.0000
display 1-_coef[cv]
.41496366
A couple of new programs have been developed for Stata that deal with Box-Cox and Box-Tidwell transform. We will show how to use them here. The first procedure is boxcox, which is available in Stata 7. This procedure finds the maximum likelihood estimate of the parameter(s) of Box-Cox transform.
xi: boxcox dep asset1 i.nation i.sector, model(lhsonly)
i.nation _Ination_1-4 (_Ination_1 for nation==CAN omitted)
i.sector _Isector_1-10 (_Isector_1 for sector==AGR omitted)
Estimating comparison model
Iteration 0: log likelihood = -1040.2744
Iteration 1: log likelihood = -917.82824
Iteration 2: log likelihood = -909.0709
Iteration 3: log likelihood = -909.05843
Iteration 4: log likelihood = -909.05843
Estimating full model
Iteration 0: log likelihood = -908.4755
Iteration 1: log likelihood = -820.15739
Iteration 2: log likelihood = -819.63494
Iteration 3: log likelihood = -819.6349
Number of obs = 248
LR chi2(13) = 178.85
Log likelihood = -819.6349 Prob > chi2 = 0.000
------------------------------------------------------------------------------
dep | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
/theta | .3063002 .0528239 5.80 0.000 .2027673 .4098331
------------------------------------------------------------------------------
Estimates of scale-variant parameters
----------------------------
| Coef.
-------------+--------------
Notrans |
asset1 | .0299857
_Ination_2 | -.1459837
_Ination_3 | -.6117602
_Ination_4 | -1.407129
_Isector_2 | -2.923013
_Isector_3 | -.9114291
_Isector_4 | .1482129
_Isector_5 | -.2716637
_Isector_6 | .0036382
_Isector_7 | .3405276
_Isector_8 | .5982639
_Isector_9 | .6550884
_Isector_10 | 1.048606
_cons | 2.115848
-------------+--------------
/sigma | 1.525277
----------------------------
---------------------------------------------------------
Test Restricted LR statistic P-Value
H0: log likelihood chi2 Prob > chi2
---------------------------------------------------------
theta = -1 -1063.8257 488.38 0.000
theta = 0 -835.82415 32.38 0.000
theta = 1 -908.4755 177.68 0.000
---------------------------------------------------------
The Box-Tidwell transformation on page 325 using data file prestige.
use https://stats.idre.ucla.edu/stat/stata/examples/ara/prestige, clear gen w2=percwomn*percwomn gen linc =income*ln(income) gen ledu =educat*ln(educat) regress prestige percwomn w2 educat income (Output omitted.) gen b1=_coef[educat] gen b2=_coef[income] regress prestige percwomn w2 educat income linc ledu (Output omitted.) gen d1=_coef[ledu] gen d2=_coef[linc] display 1+d1/b1 /*frist-step approximation on educat*/ 2.2435437 display 1+d2/b2 /*first-step approximation on income*/ -.91030351
We now use the procedure boxtid to get the fully iterated MLEs of the transformation parameters for educat and income. The boxtid command can be downloaded within Stata by typing search boxtid (see How can I use the search command to search for programs and get additional help? for more information about using search), as shown below.
boxtid regress prestige percwomn w2 educat income, df(percwomn w2:1)
Iteration 0: Deviance = 675.2403
Iteration 1: Deviance = 674.8334 (change = -.4068906)
Iteration 2: Deviance = 674.8169 (change = -.0164992)
Iteration 3: Deviance = 674.8155 (change = -.0014157)
Iteration 4: Deviance = 674.8154 (change = -.0001051)
-> gen double Ieduc__1 = educat^2.1939-182.7 if e(sample)
-> gen double Ieduc__2 = educat^2.1939*ln(educat)-433.7 if e(sample)
-> gen double Iinco__1 = X^-0.0375-1.015 if e(sample)
-> gen double Iinco__2 = X^-0.0375*ln(X)+.3916 if e(sample)
(where: X = income/10000)
-> gen double Iperc__1 = percwomn-28.98 if e(sample)
-> gen double Iw2__1 = w2-1836 if e(sample)
[Total iterations: 8]
Box-Tidwell regression model
Source | SS df MS Number of obs = 102
---------+------------------------------ F( 6, 95) = 90.29
Model | 25435.2987 6 4239.21644 Prob > F = 0.0000
Residual | 4460.12743 95 46.9487098 R-squared = 0.8508
---------+------------------------------ Adj R-squared = 0.8414
Total | 29895.4261 101 295.994318 Root MSE = 6.8519
------------------------------------------------------------------------------
prestige | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
Ieduc__1 | .0984751 .1767093 0.557 0.579 -.2523372 .4492873
Ieduc_p1 | -.0001244 .060728 -0.002 0.998 -.1206846 .1204359
Iinco__1 | -333.2435 1640.086 -0.203 0.839 -3589.226 2922.739
Iinco_p1 | .1065035 59.25056 0.002 0.999 -117.5207 117.7337
Iperc__1 | -.1658225 .0903862 -1.835 0.070 -.3452618 .0136168
Iw2__1 | .0024899 .000972 2.562 0.012 .0005603 .0044195
_cons | 47.51562 1.063237 44.690 0.000 45.40483 49.62641
------------------------------------------------------------------------------
educat | 3.806089 .3444647 11.049 Nonlin. dev. 5.019 (P = 0.031)
p1 | 2.193927 .6218453 3.528
------------------------------------------------------------------------------
income | .0011613 .00028 4.147 Nonlin. dev. 26.178 (P = 0.000)
p1 | -.0375134 .1638984 -0.229
------------------------------------------------------------------------------
Deviance: 674.815.
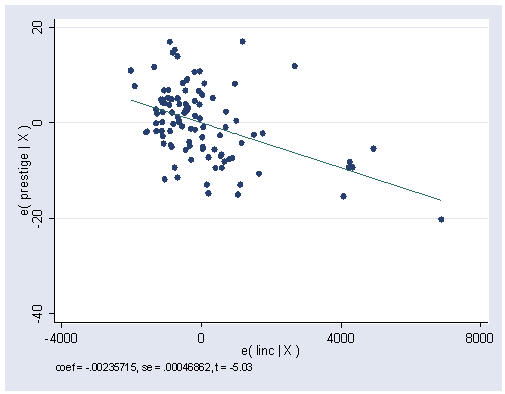
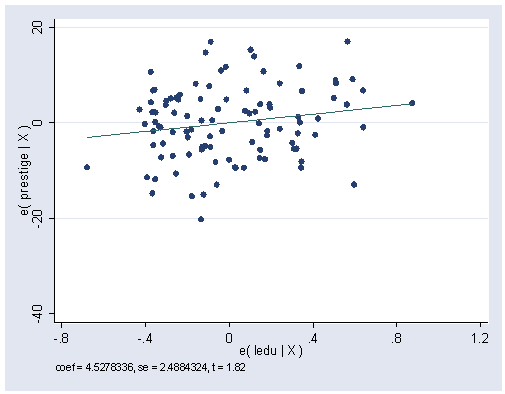
Figure 12.10. (a) and (b) on page 326 using the data file prestige. The constructed-variable plot in this case is the added variable plot for the constructed variable X*log(X).
regress prestige percwomn w2 educat income (Output omitted) avplot linc, ylabel(-40(20)20) xlabel(-4000(4000)8000)
avplot ledu, ylabel(-40(20)20) xlabel(-.8(.4)1.2)
use https://stats.idre.ucla.edu/stat/stata/examples/ara/ornstein, clear
gen asset1=sqrt(assets)
gen y=intrlcks+1
xi: regress y asset1 i.nation i.sector /*generate residuals*/
(Output omitted)
predict res, r
predict fitted, xb
gen res2=res*res
egen m= mean(res2)
gen u=res2/m /*generate U_i**/
regress u fitted
Source | SS df MS Number of obs = 248
---------+------------------------------ F( 1, 246) = 45.73
Model | 147.64882 1 147.64882 Prob > F = 0.0000
Residual | 794.296284 246 3.22884668 R-squared = 0.1567
---------+------------------------------ Adj R-squared = 0.1533
Total | 941.945104 247 3.81354293 Root MSE = 1.7969
------------------------------------------------------------------------------
u | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
fitted | .0594211 .0087872 6.762 0.000 .0421134 .0767288
_cons | .1336017 .1715663 0.779 0.437 -.2043246 .4715279
------------------------------------------------------------------------------
display 147.6488/2
73.8244
egen ybar=mean(fitted)
display 1-0.5*0.0594*ybar
.56695483
xi: regress u asset1 i.nation i.sector
i.nation Inatio_1-4 (Inatio_1 for nation==CAN omitted)
i.sector Isect_1-10 (Isect_1 for sector==AGR omitted)
Source | SS df MS Number of obs = 248
---------+------------------------------ F( 13, 234) = 4.04
Model | 172.590223 13 13.276171 Prob > F = 0.0000
Residual | 769.35488 234 3.28784137 R-squared = 0.1832
---------+------------------------------ Adj R-squared = 0.1379
Total | 941.945104 247 3.81354293 Root MSE = 1.8132
(More output omitted)