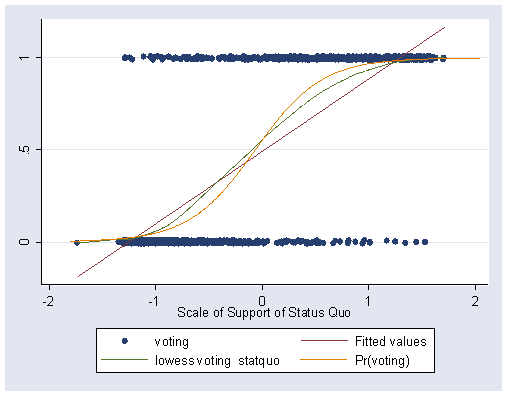
Figure 15.1 on page 440 on the data file chile.
use https://stats.idre.ucla.edu/stat/stata/examples/ara/chile, clear gen voting=1 if (intvote==1) replace voting = 0 if (intvote==2) logistic voting statquo predict pred, p graph twoway (scatter voting statquo, jitter(1)) (lfit voting statquo) /// (lowess voting statquo, bwidth(.4)) (scatter pred statquo, connect(l) msymbol(i) sort), /// ylabel(0 .5 1)
Table 15.1 and 15.2 on page 452 using the data file womenlf.
use https://stats.idre.ucla.edu/stat/stata/examples/ara/womenlf, clear
* Generating a new work status variable and an interaction variable
gen ws = 1 if( workstat==1 | workstat==2)
replace ws=0 if ( workstat==0)
gen ik = husbinc*chilpres
* Contrast between model 1 and 0 is the overall likelihood ratio of
* model 1 and the p-value is the overall Prob > chi2
xi: logistic ws husbinc i.chilpres i.region ik /*model 1 */
(Some output omitted here.)
Logit estimates Number of obs = 263
LR chi2(7) = 39.61
Prob > chi2 = 0.0000
Log likelihood = -158.27076 Pseudo R2 = 0.1112
(More output is omitted.)
lrtest, saving(m1)/* saving for further contrast test */
display -2*e(ll) /* displaying deviance */
316.54152
logistic ws /* model 0 */
display -2*e(ll)/* displaying deviance */
356.15089
xi: logistic ws husbinc i.chilpres i.region /* model 2 */
display -2*e(ll)
317.30107
lrtest, saving(m2)
lrtest, using(m1) /* contrast 2-1 */
Logistic: likelihood-ratio test chi2(1) = 0.76
Prob > chi2 = 0.3835
xi: logistic ws husbinc ik i.chilpres /* model 3 */
display -2*e(ll)
319.12422
lrtest, using(m1)/* constrast 3-1 */
Logistic: likelihood-ratio test chi2(4) = 2.58
Prob > chi2 = 0.6299
xi: logistic ws husbinc i.region /* model 4 */
display -2*e(ll)
347.84936
lrtest, using(m2)/* contrast 4-2 */
Logistic: likelihood-ratio test chi2(1) = 30.55
Prob > chi2 = 0.0000
xi: logistic ws i.chilpres i.region /* model 5 */
display -2*e(ll)
322.4267
lrtest, using(m2)/* contrast 5-2 */
Logistic: likelihood-ratio test chi2(1) = 5.13
Prob > chi2 = 0.0236
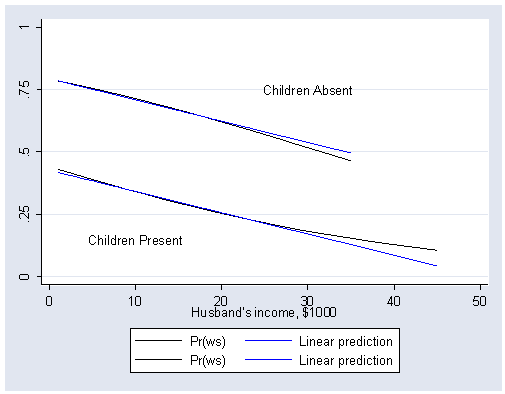
Figure 15.4 and formula on page 453.
xi: logistic ws i.chilpres husbinc
i.chilpres Ichilp_0-1 (naturally coded; Ichilp_0 omitted)
Logit estimates Number of obs = 263
LR chi2(2) = 36.42
Prob > chi2 = 0.0000
Log likelihood = -159.86627 Pseudo R2 = 0.1023
------------------------------------------------------------------------------
ws | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
Ichilp_1 | .2068734 .0604614 -5.391 0.000 .1166622 .3668421
husbinc | .9585741 .0189607 -2.139 0.032 .9221229 .9964661
------------------------------------------------------------------------------
logit
Logit estimates Number of obs = 263
LR chi2(2) = 36.42
Prob > chi2 = 0.0000
Log likelihood = -159.86627 Pseudo R2 = 0.1023
------------------------------------------------------------------------------
ws | Coef. Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
Ichilp_1 | -1.575648 .2922629 -5.391 0.000 -2.148473 -1.002824
husbinc | -.0423084 .0197801 -2.139 0.032 -.0810767 -.0035401
_cons | 1.33583 .3837632 3.481 0.000 .5836677 2.087992
------------------------------------------------------------------------------
predict pw, p
xi: regress ws i.chilpres husbinc
i.chilpres Ichilp_0-1 (naturally coded; Ichilp_0 omitted)
Source | SS df MS Number of obs = 263
---------+------------------------------ F( 2, 260) = 20.43
Model | 8.64321054 2 4.32160527 Prob > F = 0.0000
Residual | 55.0069796 260 .211565306 R-squared = 0.1358
---------+------------------------------ Adj R-squared = 0.1291
Total | 63.6501901 262 .242939657 Root MSE = .45996
------------------------------------------------------------------------------
ws | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
Ichilp_1 | -.3673736 .061906 -5.934 0.000 -.4892745 -.2454727
husbinc | -.0085375 .0039351 -2.170 0.031 -.0162863 -.0007887
_cons | .7936535 .0766814 10.350 0.000 .6426578 .9446491
------------------------------------------------------------------------------
predict lw, xb
graph twoway (scatter pw lw husbinc if chilpres ==1, sort connect(l l) msymbol(i i) clcolor(black blue)) ///
(scatter pw lw husbinc if chilpres ==0, sort connect(l l) msymbol(i i) clcolor(black blue)), ///
ttext(0.15 10 "Children Present") ttext(0.75 30 "Children Absent") ///
ylabel(0(.25)1)
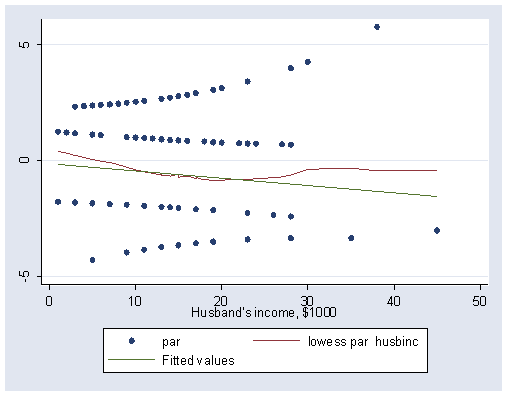
Figure 15.5 on page 459. We can’t get the exact lowess smooth as in the book as it needs more than one iterative reweighting steps as there are outliers in the data and Stata’s command lowess does not have an option on that yet. See the corresponding part of SAS for a better lowess smoothing result.
logistic ws chilpres husbinc predict prob gen par=(ws-prob)/(prob*(1-prob))-.0423*husbinc /*creating partial residual*/ graph twoway (scatter par husbinc) (lowess par husbinc, bwidth(.9)) (lfit par husbinc), /// ylabel(-5 0 5)
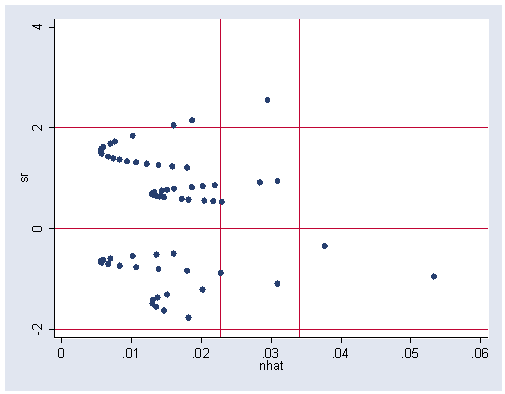
Figure 15.6 on page 461. Notice that in Stata all the diagnostic statistics for logistic regression are adjusted for the number of covariate patterns, so called m-asymptotic instead of n-asymptotic, i.e., for the number of observations. So we have to do some calculations here in order to get the results in the text book.
logistic ws chilpres husbinc predict yhat /*the predicted value*/ gen pr=(ws-yhat)/sqrt(yhat*(1-yhat)) /* generating Pearson residual on a case by case basis */ predict myhat, hat predict pattern, number egen count=count(obs), by(pattern) /*number of obs sharing a c.p.*/ gen nhat=myhat/count /*hat diagonal on per observation basis*/ gen sr = pr/sqrt(1-nhat)/*studentized pearson residual*/ graph twoway scatter sr nhat, ylabel(-2(2)4) yline(-2 0 2) xlabel(0(.01).06) xline(0.0228 .034)
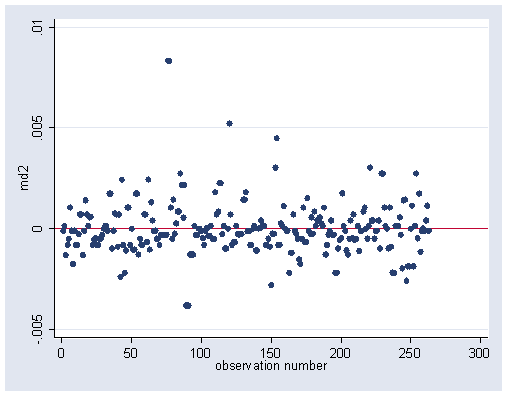
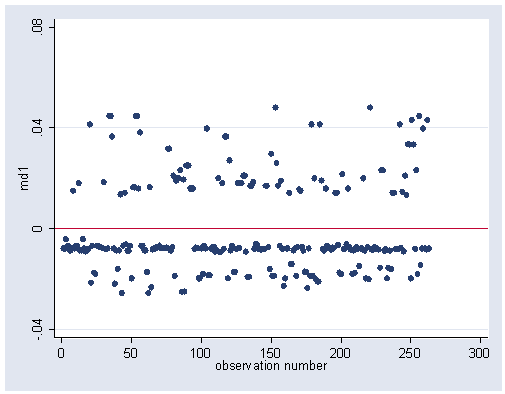
Figure 15.7 (a) and (b) on page 462. Stata does not have built-in command for Dfbeta. We use formula [15.21] to create the required statistics for these figures. This example is continuation of the previous one.
gen id=1 set matsize 300 mkmat chilpres husbinc id, matrix(X) matrix d=e(V)*X' matrix dt=d' svmat dt, name(mydf) gen md2=mydf2*(ws-yhat)/(1-nhat)/*husbincDfbeta*/ graph twoway scatter md2 obs, ylab(-0.005(0.005)0.01) yline(0) xlabel(0(50)300)
gen md1=mydf1*(ws-yhat)/(1-nhat) /*kidDfbeta*/ graph twoway scatter md1 obs, ylabel(-0.04(0.04)0.08) yline(0) xlab(0(50)300)
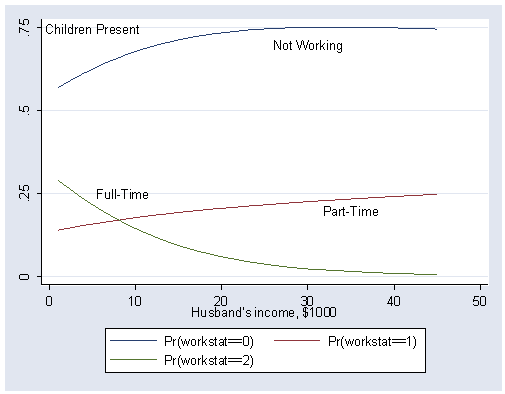
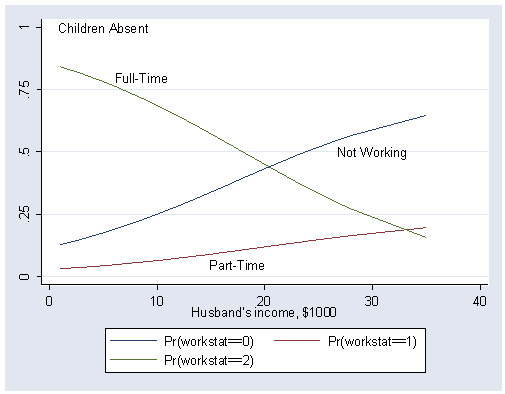
Calculation and Figure 15.8 on page 468 and 469.
mlogit workstat husbinc chilpre, base(0)
Iteration 0: log likelihood = -250.24628
Iteration 1: log likelihood = -214.24438
Iteration 2: log likelihood = -211.495
Iteration 3: log likelihood = -211.44102
Iteration 4: log likelihood = -211.44096
Multinomial regression Number of obs = 263
LR chi2(4) = 77.61
Prob > chi2 = 0.0000
Log likelihood = -211.44096 Pseudo R2 = 0.1551
------------------------------------------------------------------------------
workstat | Coef. Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
parttime |
husbinc | .0068921 .0234548 0.294 0.769 -.0390784 .0528627
chilpres | .0214911 .4690366 0.046 0.963 -.8978037 .940786
_cons | -1.432307 .5924623 -2.418 0.016 -2.593512 -.2711023
---------+--------------------------------------------------------------------
fulltime |
husbinc | -.0972307 .0280958 -3.461 0.001 -.1522975 -.0421639
chilpres | -2.558595 .362199 -7.064 0.000 -3.268492 -1.848698
_cons | 1.982822 .4841771 4.095 0.000 1.033853 2.931792
------------------------------------------------------------------------------
(Outcome workstat==not work is the comparison group)
predict p0 p1 p2
graph twoway (line p0 husbinc if chilpres==1, sort) (line p1 husbinc if chilpres==1, sort) ///
(line p2 husbinc if chilpres==1, sort) , ylabel(0(.25).75) ///
ttext(0.75 5 "Children Present") ttext(0.70 30 "Not Working") ///
ttext(0.25 8.5 "Full-Time") ttext(0.20 35 "Part-Time")
graph twoway (line p0 husbinc if chilpres==0, sort) (line p1 husbinc if chilpres==0, sort) /// (line p2 husbinc if chilpres==0, sort) , ylabel(0(.25)1) /// ttext(1 5 "Children Absent") ttext(0.50 30 "Not Working") /// ttext(0.80 8.5 "Full-Time") ttext(0.05 17.5 "Part-Time")
Calculation on page 473.
gen wk=(workstat==0)
logistic wk husbinc chilpres
Logit estimates Number of obs = 263
LR chi2(2) = 36.42
Prob > chi2 = 0.0000
Log likelihood = -159.86627 Pseudo R2 = 0.1023
------------------------------------------------------------------------------
wk | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
husbinc | 1.043216 .0206349 2.139 0.032 1.003546 1.084454
chilpres | 4.833875 1.412762 5.391 0.000 2.725968 8.57176
------------------------------------------------------------------------------
logit
Logit estimates Number of obs = 263
LR chi2(2) = 36.42
Prob > chi2 = 0.0000
Log likelihood = -159.86627 Pseudo R2 = 0.1023
------------------------------------------------------------------------------
wk | Coef. Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
husbinc | .0423084 .0197801 2.139 0.032 .0035401 .0810767
chilpres | 1.575648 .2922629 5.391 0.000 1.002824 2.148473
_cons | -1.33583 .3837632 -3.481 0.000 -2.087992 -.5836677
------------------------------------------------------------------------------
lrtest, saving(0)
logistic wk chilpres
Logit estimates Number of obs = 263
LR chi2(1) = 31.59
Prob > chi2 = 0.0000
Log likelihood = -162.27945 Pseudo R2 = 0.0887
------------------------------------------------------------------------------
wk | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
chilpres | 4.781119 1.379609 5.422 0.000 2.71589 8.416797
------------------------------------------------------------------------------
lrtest /*test on the bottom of page 473*/
Logistic: likelihood-ratio test chi2(1) = 4.83
Prob > chi2 = 0.0280
gen ptime=.
replace ptime = 0 if (workstat==1)
replace ptime=1 if(workstat==2)
logistic ptime husbinc chilpres
Logit estimates Number of obs = 108
LR chi2(2) = 39.85
Prob > chi2 = 0.0000
Log likelihood = -52.247423 Pseudo R2 = 0.2761
------------------------------------------------------------------------------
ptime | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
husbinc | .898285 .0351699 -2.740 0.006 .8319318 .9699305
chilpres | .0705484 .0381719 -4.900 0.000 .0244301 .2037278
------------------------------------------------------------------------------
logit
Logit estimates Number of obs = 108
LR chi2(2) = 39.85
Prob > chi2 = 0.0000
Log likelihood = -52.247423 Pseudo R2 = 0.2761
------------------------------------------------------------------------------
ptime | Coef. Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
husbinc | -.1072679 .0391522 -2.740 0.006 -.1840048 -.0305309
chilpres | -2.651456 .5410738 -4.900 0.000 -3.711941 -1.59097
_cons | 3.477773 .7671069 4.534 0.000 1.974272 4.981275
------------------------------------------------------------------------------
lrtest, saving(p1)
logistic ptime chilpres
Logit estimates Number of obs = 108
LR chi2(1) = 30.87
Prob > chi2 = 0.0000
Log likelihood = -56.738094 Pseudo R2 = 0.2138
------------------------------------------------------------------------------
ptime | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
chilpres | .0869565 .04288 -4.953 0.000 .0330794 .2285846
------------------------------------------------------------------------------
lrtest, using(p1)/*test on the top of page 474*/
Logistic: likelihood-ratio test chi2(1) = 8.98
Prob > chi2 = 0.0027
Calculation on page 477.
xi: ologit workstat husbinc i.chilpres
i.chilpres Ichilp_0-1 (naturally coded; Ichilp_0 omitted)
Iteration 0: log likelihood = -250.24628
Iteration 1: log likelihood = -221.36758
Iteration 2: log likelihood = -220.83242
Iteration 3: log likelihood = -220.83148
Ordered logit estimates Number of obs = 263
LR chi2(2) = 58.83
Prob > chi2 = 0.0000
Log likelihood = -220.83148 Pseudo R2 = 0.1175
------------------------------------------------------------------------------
workstat | Coef. Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
husbinc | -.0539007 .01949 -2.766 0.006 -.0921004 -.0157009
Ichilp_1 | -1.971957 .2869478 -6.872 0.000 -2.534364 -1.40955
---------+--------------------------------------------------------------------
_cut1 | -1.852037 .3862995 (Ancillary parameters)
_cut2 | -.9409253 .3699303
------------------------------------------------------------------------------
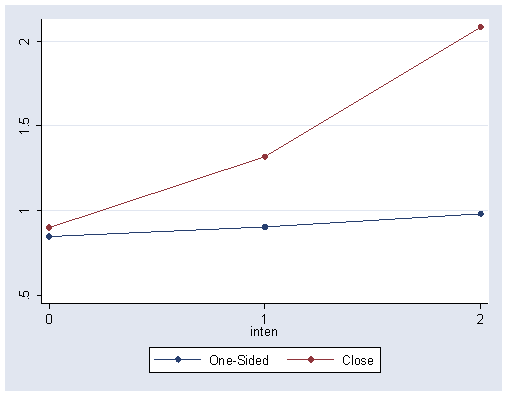
The analysis in this section is based on table 15.3, which is based on data from an example from The American Voter (Campbell, et al., 1960). The first data set we create here is based on table 15.3 for figure 15.3 (page 480).
input logv1 logvc inten 847 .9 0 904 1.318 1 981 2.084 2 end label define scale 0 Weak 1 Medium 2 Strong label values inten scale label variable logv1 "One-Sided" label variable logvc "Close" graph twoway scatter logv1 logvc inten, connect(l l) xlabel(0 1 2)
Now we create another data set below to do the logistic regression and tests over different models. Thus we will have table 15.4 and table 15.5 on page 482.
input perclose inten1 inten2 voted wv
0 0 0 1 91
0 0 0 0 39
0 1 0 1 121
0 1 0 0 49
0 0 1 1 64
0 0 1 0 24
1 0 0 1 214
1 0 0 0 87
1 1 0 1 284
1 1 0 0 76
1 0 1 1 201
1 0 1 0 25
end
gen clspref1=perclose*inten1
gen clspref2=perclose*inten2
logistic voted perclose inten1 inten2 clspref1 clspref2 [fweight=wv]
(Output omitted.)
di -2*e(ll) /*deviance for model 1*/
1356.4343
lrtest, saving(t1)
logistic voted perclose inten1 inten2 [fweight=wv]
(Output omitted.)
di -2*e(ll) /*model 2*/
1363.5529
lrtest, saving(t2)
lrtest, using(t1)/*contrast 2-1*/
Logistic: likelihood-ratio test chi2(2) = 7.12
Prob > chi2 = 0.0285
logistic voted perclose clspref1 clspref2 [fweight=wv]
(Output omitted.)
di -2*e(ll) /*model 3 */
1356.6253
lrtest, saving(t3)
lrtest, using(t1) /*contrast 3-1 */
Logistic: likelihood-ratio test chi2(2) = 0.19
Prob > chi2 = 0.9089
logistic voted inten1 inten2 clspref1 clspref2 [fweight=wv]
(Output omitted.)
di -2*e(ll) /*model 4*/
1356.4869
lrtest, using(t1)
Logistic: likelihood-ratio test chi2(1) = 0.05
Prob > chi2 = 0.8186
logistic voted perclose [fweight=wv]
(Output omitted.)
di -2*e(ll) /*model 5 */
1382.6582
lrtest, using(t2)
Logistic: likelihood-ratio test chi2(2) = 19.11
Prob > chi2 = 0.0001
logistic voted inten1 inten2 [fweight=wv]
(Output omitted.)
di -2*e(ll) /*model 6*/
1371.8382
lrtest, using(t2)
Logistic: likelihood-ratio test chi2(1) = 8.29
Prob > chi2 = 0.0040