Regression analysis middle of page 269. Make measwt by female interaction and then run regression with the interaction.
use https://stats.idre.ucla.edu/stat/stata/examples/ara/davis, clear generate measwt_f = measwt * female regress reptwt measwt female measwt_f Source | SS df MS Number of obs = 183 ---------+------------------------------ F( 3, 179) = 470.41 Model | 30654.7294 3 10218.2431 Prob > F = 0.0000 Residual | 3888.25423 179 21.7220907 R-squared = 0.8874 ---------+------------------------------ Adj R-squared = 0.8856 Total | 34542.9836 182 189.796613 Root MSE = 4.6607 ------------------------------------------------------------------------------ reptwt | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- measwt | .9898221 .0425995 23.236 0.000 .9057602 1.073884 female | 39.96412 3.929322 10.171 0.000 32.21037 47.71787 measwt_f | -.7253627 .0559804 -12.957 0.000 -.8358292 -.6148963 _cons | 1.35864 3.277192 0.415 0.679 -5.108262 7.825541 ------------------------------------------------------------------------------
Save version with error (for use later) as davis_er.
save davis_er, replace file davis_er.dta saved
Regression at bottom of 269. Fix error in case 12, and run the regression from above again. Fix error in case 12.
generate t = measwt in 12 (199 missing values generated) replace measwt = measht in 12 (1 real change made) replace measht = t in 12 (1 real change made) drop t
Make measwt by female interaction again.
replace measwt_f = measwt * female
Run regression.
regress reptwt measwt female measwt_f Source | SS df MS Number of obs = 183 ---------+------------------------------ F( 3, 179) = 2228.78 Model | 33642.3446 3 11214.1149 Prob > F = 0.0000 Residual | 900.638968 179 5.03150261 R-squared = 0.9739 ---------+------------------------------ Adj R-squared = 0.9735 Total | 34542.9836 182 189.796613 Root MSE = 2.2431 ------------------------------------------------------------------------------ reptwt | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- measwt | .9898221 .0205023 48.279 0.000 .9493648 1.030279 female | 1.982518 2.450282 0.809 0.420 -2.852638 6.817673 measwt_f | -.0566831 .0384548 -1.474 0.142 -.1325662 .0191999 _cons | 1.35864 1.577248 0.861 0.390 -1.753752 4.471032 ------------------------------------------------------------------------------
Save corrected version (for use later) as davis_co.
save davis_co, replace file davis_co.dta saved
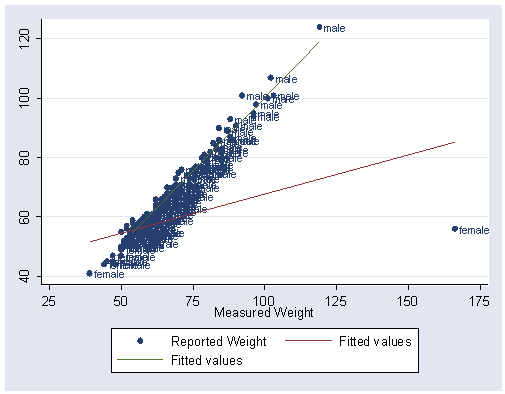
Page 270, figure 11.2. Show graph similar to figure 11.2 showing outlier. Use the data file with the error.
use https://stats.idre.ucla.edu/stat/stata/examples/ara/davis_er, clear
Run the regression.
regress reptwt measwt female measwt_f Source | SS df MS Number of obs = 183 ---------+------------------------------ F( 3, 179) = 470.41 Model | 30654.7294 3 10218.2431 Prob > F = 0.0000 Residual | 3888.25423 179 21.7220907 R-squared = 0.8874 ---------+------------------------------ Adj R-squared = 0.8856 Total | 34542.9836 182 189.796613 Root MSE = 4.6607 ------------------------------------------------------------------------------ reptwt | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- measwt | .9898221 .0425995 23.236 0.000 .9057602 1.073884 female | 39.96412 3.929322 10.171 0.000 32.21037 47.71787 measwt_f | -.7253627 .0559804 -12.957 0.000 -.8358292 -.6148963 _cons | 1.35864 3.277192 0.415 0.679 -5.108262 7.825541 ------------------------------------------------------------------------------
predict yhat graph twoway (scatter reptwt measwt, mlabel(female)) (line yhat measwt if female == 1, sort) /// (line yhat measwt if female == 0, sort), xlabel(25(25)175)
Middle of page 270, regression analysis. (Note errata: last term should be reptwt x female). Stata results match the results in Fox.
generate reptwt_f = reptwt * female (17 missing values generated) regress measwt reptwt female reptwt_f Source | SS df MS Number of obs = 183 ---------+------------------------------ F( 3, 179) = 139.07 Model | 29786.3783 3 9928.79278 Prob > F = 0.0000 Residual | 12779.4359 179 71.3934965 R-squared = 0.6998 ---------+------------------------------ Adj R-squared = 0.6947 Total | 42565.8142 182 233.8781 Root MSE = 8.4495 ------------------------------------------------------------------------------ measwt | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- reptwt | .9689183 .0764096 12.681 0.000 .8181387 1.119698 female | 2.074211 9.297269 0.223 0.824 -16.27214 20.42056 reptwt_f | -.0095251 .1468546 -0.065 0.948 -.2993141 .2802639 _cons | 1.79428 5.923944 0.303 0.762 -9.89547 13.48403 ------------------------------------------------------------------------------
Page 271, make hat value and show largest hat values.
Run the regression.
regress reptwt measwt female measwt_f Source | SS df MS Number of obs = 183 ---------+------------------------------ F( 3, 179) = 470.41 Model | 30654.7294 3 10218.2431 Prob > F = 0.0000 Residual | 3888.25423 179 21.7220907 R-squared = 0.8874 ---------+------------------------------ Adj R-squared = 0.8856 Total | 34542.9836 182 189.796613 Root MSE = 4.6607 ------------------------------------------------------------------------------ reptwt | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- measwt | .9898221 .0425995 23.236 0.000 .9057602 1.073884 female | 39.96412 3.929322 10.171 0.000 32.21037 47.71787 measwt_f | -.7253627 .0559804 -12.957 0.000 -.8358292 -.6148963 _cons | 1.35864 3.277192 0.415 0.679 -5.108262 7.825541 ------------------------------------------------------------------------------
Generate hat values, calling the result myhat.
predict myhat, hat
Middle of page 271, get the largest hat value, .714.
summarize myhat, detail
Leverage
-------------------------------------------------------------
Percentiles Smallest
1% .0099067 .0099067
5% .0099302 .0099067
10% .0101496 .0099067 Obs 200
25% .0110274 .0099067 Sum of Wgt. 200
50% .0131432 Mean .0212232
Largest Std. Dev. .0514178
75% .0185647 .0687759
90% .0285695 .0732077 Variance .0026438
95% .0456122 .1668405 Skewness 12.45924
99% .1200241 .7141857 Kurtosis 166.9527
Lower part of page 271, subject 12 has the hat value over .7.
list subject myhat if myhat > .7
subject myhat
12. 12 .7141857
Page 274, middle of page. Make studentized residual and show largest value.
Make residual.
predict res, rstud (17 missing values generated)
Get the largest studentized residual, -24.3.
summarize res, detail
Studentized residuals
-------------------------------------------------------------
Percentiles Smallest
1% -2.349376 -24.30446
5% -1.466444 -2.349376
10% -.9816217 -2.189853 Obs 183
25% -.5037653 -1.959426 Sum of Wgt. 183
50% -.0284926 Mean -.0961781
Largest Std. Dev. 2.008318
75% .4462518 2.393195
90% 1.040694 2.90657 Variance 4.033341
95% 1.566641 3.081378 Skewness -9.557869
99% 3.081378 3.496628 Kurtosis 116.8471
Subject 12 had the largest residual.
list subject res if res < -24.3
subject res
12. 12 -24.30446
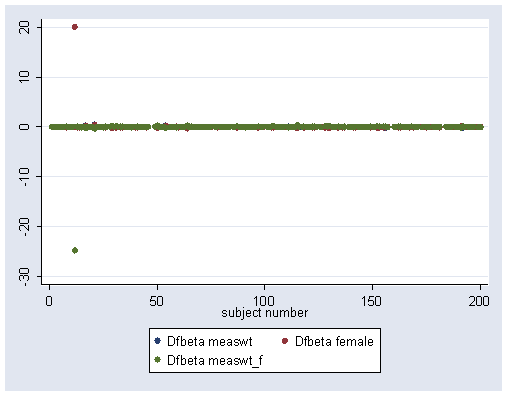
Middle of page 276, computing DFBETA and making index plot (plot described but not shown). The dfbeta command computes the DFBETA for measwt (called DFmeaswt), for female (called DFfemale, and for measwt_f (called DF1).
dfbeta (17 missing values generated) DFmeaswt: DFbeta(measwt) (17 missing values generated) DFfemale: DFbeta(female) (17 missing values generated) DF1: DFbeta(measwt_f)
Index plot shows an observation influencing female and influencing female*measwt.
rename DFmeaswt_f DF1 graph twoway scatter DFmeaswt DFfemale DF1 subject
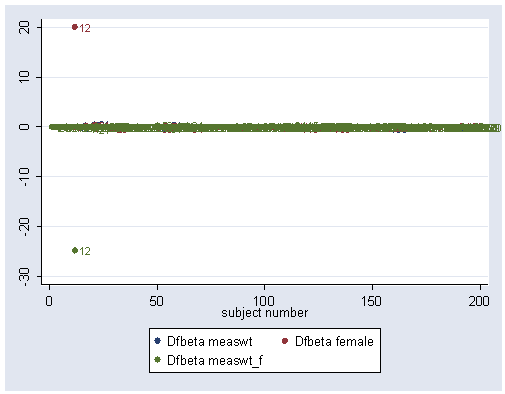
Show same plot, but use subject number as symbol to identify which subject has influential data. It is subject 12.
graph twoway scatter DFmeaswt DFfemale DF1 subject, mlabel(subject subject subject)
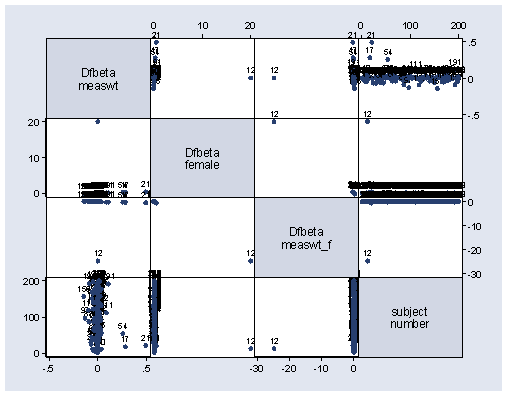
Scatterplot of dfbetas, suggested near bottom page 276.
graph matrix DFmeaswt DFfemale DF1 subject, mlabel(subject)
Bottom part of page 277, computing and showing Cook’s D, DFFITS, DFBETAS.
Already computed DFBETA above using dfbeta command.
Compute Cook’s D.
predict d, cooksd (17 missing values generated)
Compute DFFITS.
predict dfit, dfits (17 missing values generated)
Use summarize to get largest values of cooks d, dffits, dfbeta like bottom of 277.
summarize d dfit DFmeaswt DFfemale DF1 , detail
Cook's D
-------------------------------------------------------------
Percentiles Smallest
1% 2.11e-06 2.11e-06
5% .0000228 2.11e-06
10% .000026 2.11e-06 Obs 183
25% .0001244 .0000157 Sum of Wgt. 183
50% .0007961 Mean .4738773
Largest Std. Dev. 6.351621
75% .0032174 .0651359
90% .0096058 .0701759 Variance 40.34309
95% .0199879 .0856294 Skewness 13.41655
99% .0856294 85.92735 Kurtosis 181.0043
Dfits
-------------------------------------------------------------
Percentiles Smallest
1% -.4308479 -38.41931
5% -.1958499 -.4308479
10% -.1174221 -.296132 Obs 183
25% -.0592021 -.2823458 Sum of Wgt. 183
50% -.0028959 Mean -.2012365
Largest Std. Dev. 2.843795
75% .0560052 .5108672
90% .1362741 .5115646 Variance 8.087169
95% .2121069 .540725 Skewness -13.37203
99% .540725 .6033236 Kurtosis 180.215
DFmeaswt
-------------------------------------------------------------
Percentiles Smallest
1% -.1318417 -.1449406
5% -.059406 -.1318417
10% -.0427876 -.0978029 Obs 183
25% -.0000766 -.0921938 Sum of Wgt. 183
50% -5.92e-16 Mean .0003997
Largest Std. Dev. .0540191
75% 1.22e-16 .1096412
90% .0141305 .2565254 Variance .0029181
95% .0314289 .2809305 Skewness 5.222216
99% .2809305 .4918421 Kurtosis 45.52623
DFfemale
-------------------------------------------------------------
Percentiles Smallest
1% -.2217265 -.2219922
5% -.1140623 -.2217265
10% -.063526 -.2097966 Obs 183
25% -.0294111 -.1823008 Sum of Wgt. 183
50% -.0050063 Mean .0941992
Largest Std. Dev. 1.482754
75% .0039615 .1956965
90% .0166306 .2036534 Variance 2.198559
95% .0342111 .3870315 Skewness 13.38578
99% .3870315 20.02775 Kurtosis 180.4558
DF1
-------------------------------------------------------------
Percentiles Smallest
1% -.3742779 -24.7525
5% -.0256302 -.3742779
10% -.0133058 -.2137802 Obs 183
25% -.0021874 -.1952085 Sum of Wgt. 183
50% .0054611 Mean -.1163372
Largest Std. Dev. 1.832269
75% .0328629 .2331503
90% .0701569 .2636165 Variance 3.35721
95% .1102957 .2943538 Skewness -13.39209
99% .2943538 .3174025 Kurtosis 180.5693
We can see these values for subject 12.
list d dfit DFmeaswt DFfemale DF1 if subject==12
d dfit DFmeaswt DFfemale DF1
12. 85.92735 -38.41931 8.62e-13 20.02775 -24.7525
Top of page 279, computing COVRATIO. We can compute a variable covrat containing the COVRATIO.
predict covrat, covratio (17 missing values generated)
Look at summary stats for covrat.
summarize covrat Variable | Obs Mean Std. Dev. Min Max ---------+----------------------------------------------------- covrat | 183 1.018453 .0833018 .0102869 1.19215
You can see that subject 12 has smallest covrat.
list subject covrat if covrat < .02
subject covrat
12. 12 .0102869
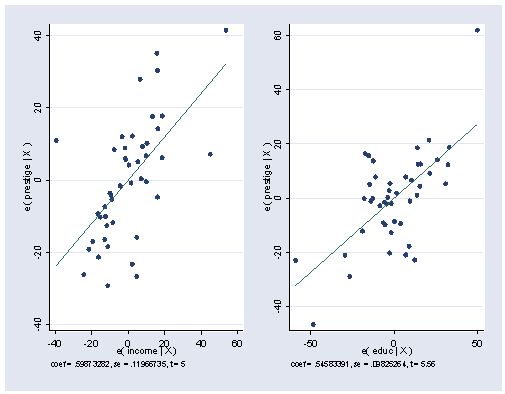
Page 283 bottom, and figure 11.5 page 284, partial regression plots.
use https://stats.idre.ucla.edu/stat/stata/examples/ara/duncan, clear
Fit regression at bottom of page 283.
regress prestige income educ
Source | SS df MS Number of obs = 45
---------+------------------------------ F( 2, 42) = 101.22
Model | 36180.9458 2 18090.4729 Prob > F = 0.0000
Residual | 7506.69865 42 178.73092 R-squared = 0.8282
---------+------------------------------ Adj R-squared = 0.8200
Total | 43687.6444 44 992.90101 Root MSE = 13.369
------------------------------------------------------------------------------
prestige | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
income | .5987328 .1196673 5.003 0.000 .3572343 .8402313
educ | .5458339 .0982526 5.555 0.000 .3475521 .7441158
_cons | -6.064663 4.271941 -1.420 0.163 -14.68579 2.556463
------------------------------------------------------------------------------
Figure 11.5 on page 284 can be obtained by using the avplots command.
avplots
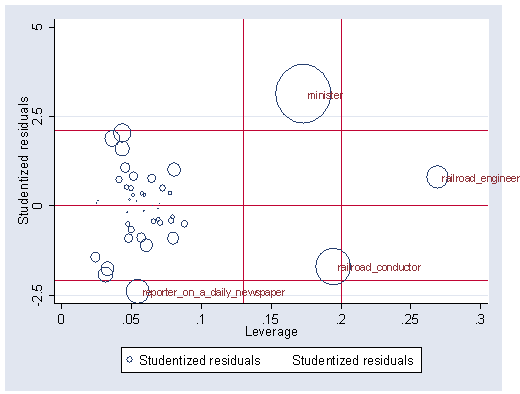
Middle of page 284 influence statistics, and figure 11.6 on page 285.
Make and show hat, residual, Cook’s D.
predict hat1, hat
predict res, rstud
predict d, cooksd
summarize hat1 res d, detail
Leverage
-------------------------------------------------------------
Percentiles Smallest
1% .0241298 .0241298
5% .0262859 .0246816
10% .0327049 .0262859 Obs 45
25% .0467892 .031326 Sum of Wgt. 45
50% .05732 Mean .0666667
Largest Std. Dev. .0438265
75% .0705812 .0878518
90% .082588 .1730582 Variance .0019208
95% .1730582 .1945416 Skewness 3.050461
99% .2690896 .2690896 Kurtosis 13.16723
Studentized residuals
-------------------------------------------------------------
Percentiles Smallest
1% -2.397022 -2.397022
5% -1.760491 -1.930919
10% -1.433249 -1.760491 Obs 45
25% -.4980818 -1.704032 Sum of Wgt. 45
50% .0505098 Mean .006828
Largest Std. Dev. 1.055861
75% .5083882 1.602429
90% 1.068858 1.887047 Variance 1.114843
95% 1.887047 2.043805 Skewness .296872
99% 3.134519 3.134519 Kurtosis 3.928454
Cook's D
-------------------------------------------------------------
Percentiles Smallest
1% 1.20e-08 1.20e-08
5% .0000537 .0000128
10% .0001334 .0000537 Obs 45
25% .0016885 .0000784 Sum of Wgt. 45
50% .0058424 Mean .0317011
Largest Std. Dev. .0898235
75% .0236292 .0809681
90% .0585235 .0989846 Variance .0080683
95% .0989846 .2236412 Skewness 5.064094
99% .5663797 .5663797 Kurtosis 29.68371
Figure 11.6on page 285. Scatterplot of rstud and hat weighted by cooksd. Observations with a hat value larger than 0.13 had their occupational title specified by the mlabel(occtitle) option.
graph twoway (scatter res hat1 [w=d],msymbol(Oh)) /// (scatter res hat1 if res <= -2.1 | hat1 >= .13, mlabel(occtitle) msymbol(i)), /// xlabel(0(.05).3) ylabel(-2.5(2.5)5) yline(-2.1 0 2.1) xline(.13 .20)