Table 2.1, Table 2.2, and Figure 2.1 on pages 17, 20, and 21. The lean1 scheme is used for the graphs on this page. To download this Stata scheme, use the search command. For these examples, we are entering a dataset.
input subject time censor 1 6 1 2 44 1 3 21 0 4 14 1 5 62 1 end
list, clean
subject time censor
1. 1 6 1
2. 2 44 1
3. 3 21 0
4. 4 14 1
5. 5 62 1
stset time, id(subject) failure(censor)
sts list
failure _d: censor
analysis time _t: time
id: subject
Beg. Net Survivor Std.
Time Total Fail Lost Function Error [95% Conf. Int.]
-------------------------------------------------------------------------------
6 5 1 0 0.8000 0.1789 0.2038 0.9692
14 4 1 0 0.6000 0.2191 0.1257 0.8818
21 3 0 1 0.6000 0.2191 0.1257 0.8818
44 2 1 0 0.3000 0.2387 0.0123 0.7192
62 1 1 0 0.0000 . . .
-------------------------------------------------------------------------------
sts graph, xlabel(0(12)60) ylabel(0(.2)1, nogrid angle(horizontal)) ///
xtitle(Survival Time) ytitle(Esitmated Survival Probabiltiy) ///
title(Figure 2.1)
failure _d: censor
analysis time _t: time
id: subject
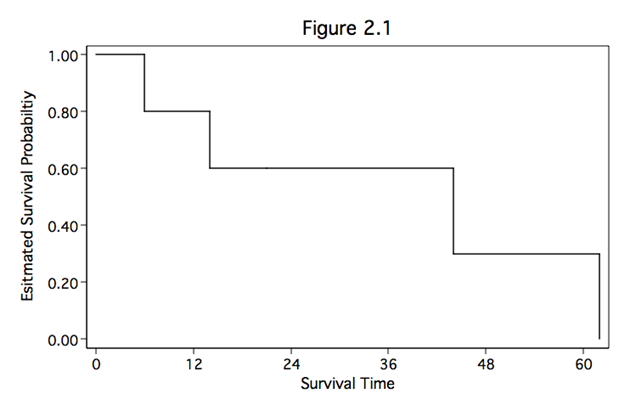
Figure 2.2 on page 22. This graph is generated using the whas100 dataset.
use https://stats.idre.ucla.edu/stat/examples/asa2/whas100, clear
gen fyear=foltime/365.25
stset fyear, id(id) failure(folstatus)
sts graph, xlabel(0(2)8) ylabel(0(.2)1, nogrid angle(horizontal)) ///
xtitle(Survival Time (Years)) ytitle(Estimated Survival Probability) ///
title(Figure 2.2)
failure _d: folstatus
analysis time _t: fyear
id: id
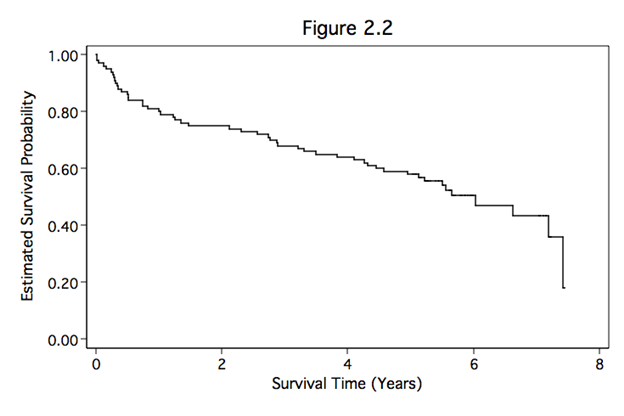
Table 2.3 on page 23 using the whas100 dataset.
stset foltime, fail(folstatus)
sts list, enter
failure _d: folstatus
analysis time _t: foltime
Beg. Survivor Std.
Time Total Fail Lost Enter Function Error [95% Conf. Int.]
-------------------------------------------------------------------------------
0 0 0 0 100 1.0000 . . .
6 100 2 0 0 0.9800 0.0140 0.9224 0.9950
14 98 1 0 0 0.9700 0.0171 0.9099 0.9902
44 97 1 0 0 0.9600 0.0196 0.8969 0.9848
62 96 1 0 0 0.9500 0.0218 0.8840 0.9789
89 95 1 0 0 0.9400 0.0237 0.8713 0.9726
...additional output omitted...
2641 3 0 1 0 0.3606 0.0857 0.1997 0.5241
2710 2 1 0 0 0.1803 0.1345 0.0179 0.4820
2719 1 0 1 0 0.1803 0.1345 0.0179 0.4820
-------------------------------------------------------------------------------
Table 2.4 on page 24 using the whas100 dataset.
stset fyear, id(id) failure(folstatus)
ltable fyear folstatus, saving(ltable1, replace)
Beg. Std.
Interval Total Deaths Lost Survival Error [95% Conf. Int.]
-------------------------------------------------------------------------------
0 1 100 20 0 0.8000 0.0400 0.7074 0.8660
1 2 80 5 0 0.7500 0.0433 0.6529 0.8236
2 3 75 7 0 0.6800 0.0466 0.5790 0.7617
3 4 68 4 0 0.6400 0.0480 0.5377 0.7254
4 5 64 6 0 0.5800 0.0494 0.4772 0.6696
5 6 58 5 39 0.5047 0.0532 0.3965 0.6032
6 7 14 2 0 0.4326 0.0656 0.3027 0.5556
7 8 12 2 10 0.3090 0.0875 0.1520 0.4808
-------------------------------------------------------------------------------
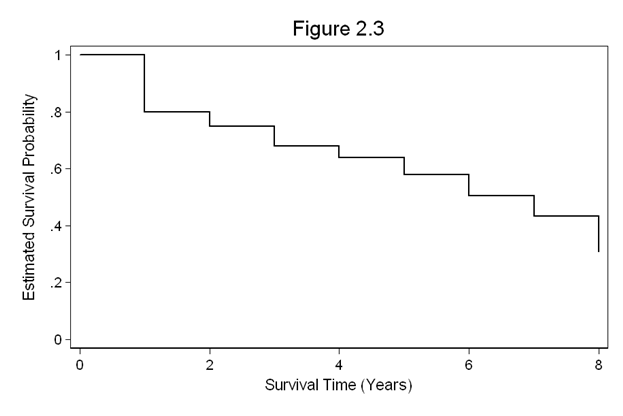
Figure 2.3 on page 25. This graph is produced using a dataset created in the previous example (ltable1).
use https://stats.idre.ucla.edu/stat/examples/asa2/ltable1, clear set obs 9 replace t1=0 in l replace survival=1 in l sort t1 twoway line survival t1, con(J) ylabel(0(.2)1) /// xlabel(0(2)8) xtitle(Survival Time (Years)) ytitle(Estimated Survival Probability) /// title(Figure 2.3)
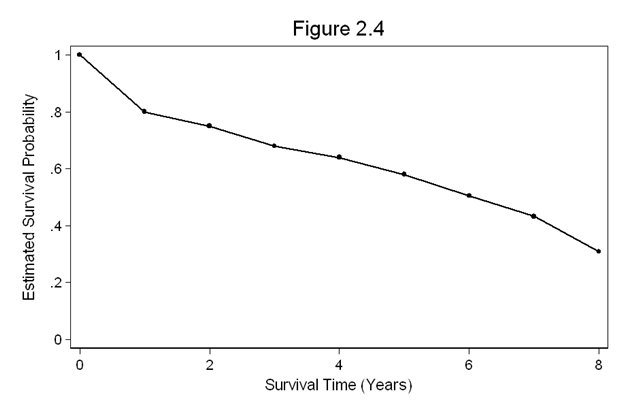
Figure 2.4 on page 26. This graph depicts the polygon representation of the life-table estimate from the dataset in the above example (ltable1).
twoway connect survival t1, msymbol(o) ylabel(0(.2)1) /// xlabel(0(2)8) xtitle(Survival Time (Years)) ytitle(Estimated Survival Probability) /// title(Figure 2.4)
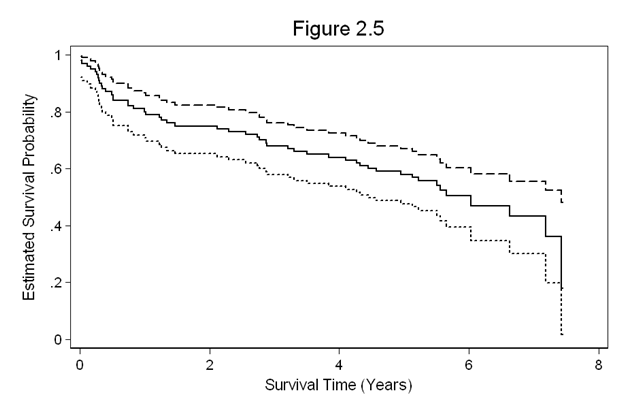
Figure 2.5 on page 31 using the whas100 dataset.
use https://stats.idre.ucla.edu/stat/examples/asa2/whas100, clear gen fyear = foltime/365.25 stset fyear, id(id) failure(folstatus) sts gen s=s se=se(s) ub=ub(s) lb=lb(s) sort fyear twoway (line s fyear, con(J))(line ub fyear, con(J))(line lb fyear, con(J)), /// legend(off) xtitle(Survival Time (Years)) ytitle(Estimated Survival Probability) /// title(Figure 2.5)
Figure 2.6 on page 32. For this figure, we continue to use the whas100 dataset from the example above.
* log-log transformation
gen ll_s = se/(s*ln(s))
gen ll_l = exp(- exp(ln(-ln(s)) - 1.96*ll_s))
gen ll_u = exp(- exp(ln(-ln(s)) + 1.96*ll_s))
* log transformation, formula 2.3
gen log_s = se/s
gen log_l = s*exp( - 1.96*log_s)
gen log_u = s*exp( 1.96*log_s)
* logit transformation. f'=1/(S(t)*(1-S(t))
gen logit_s = se/(s*(1-s))
gen logit_surv = ln(s/(1-s))
gen logit_l = exp(logit_surv - 1.96*logit_s)/(1+exp(logit_surv - 1.96*logit_s))
gen logit_u = exp(logit_surv + 1.96*logit_s)/(1+exp(logit_surv + 1.96*logit_s))
* arcsine transformation
gen arcs_s = se/sqrt(1-s^2)
gen arcs_surv = asin(s)
gen arcs_l = sin(arcs_surv - 1.96*arcs_s)
gen arcs_u = sin(arcs_surv + 1.96*arcs_s)
sort fyear
twoway (line s fyear, con(J)) ///
(line ll_u ll_l fyear, con(J J) lpattern(dash dash) lcolor(black black)) ///
(line log_u log_l fyear, con(J J) lpattern(dash_dot dash_dot) lcolor(black black)) ///
(line logit_u logit_l fyear, con(J J) lpattern(longdash longdash) lcolor(black black)) ///
(line arcs_u arcs_l fyear, con(J J) lpattern(shortdash shortdash) lcolor(black black)), ///
l2title(Estimated Survival Probability, size(medsmall)) ///
legend(off) ylabel(,nogrid angle(horizontal)) yscale(titlegap(3)) xscale(titlegap(3)) ///
xtitle(Survival Time (Years)) title(Figure 2.6)
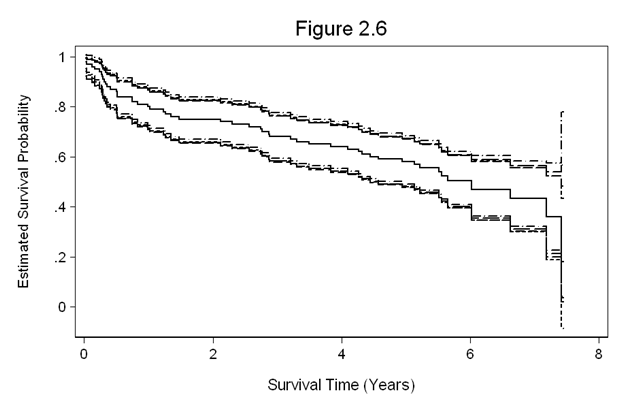
Figure 2.7 on page 34 using the whas100 dataset.
use https://stats.idre.ucla.edu/stat/examples/asa2/whas100, clear
gen fyear = foltime/365.25
stset fyear, failure(folstatus)
sts gen s=s se=se(s) ub=ub(s) lb=lb(s)
* compute the variance of the log of the Kaplan-Meier estimateor
gen sigma2 = se^2/s^2
* what is H_a_alpha in formula (29)?
* compute "a" first. Notice that the largest noncensored vlaue of time is 2710, or 7.42 years
* n = 100 cases
* notice the value for sigma2 when time = 7.42 is .557
* a = 100*557/(1+100*557)
* looking up the table from Appendix 3: we get H = 1.358
gen bl = ln(-ln(s)) - 1.358*(1+100*sigma2)/(sqrt(100)*ln(s))
gen bu = ln(-ln(s)) + 1.358*(1+100*sigma2)/(sqrt(100)*ln(s))
gen ebl = exp(-exp(bu))
gen ebu = exp(-exp(bl))
gen var2_6 = se^2/(s^2*(ln(s))^2)
gen cl =ln(-ln(s)) - 1.96*sqrt(var2_6)
gen cu =ln(-ln(s)) + 1.96*sqrt(var2_6)
gen l = exp(-exp(cu))
gen u = exp(-exp(cl))
sort fyear
twoway (line s fyear, c(J) clcolor(black)) ///
(line ebl ebu fyear, c(J J) clcolor(black black) clpattern("-..-" "-..-") ) ///
(line l u fyear, c(J J) clcolor(black black) clpattern("-" "-")) , ///
yscale(range(0(0.2)1)) l2title(Estimated Survival Probability, size(medsmall)) ///
legend( off) ylabel(,nogrid angle(horizontal)) yscale(titlegap(3)) xscale(titlegap(3)) ///
xtitle(Survival Time (Years)) title(Figure 2.7)
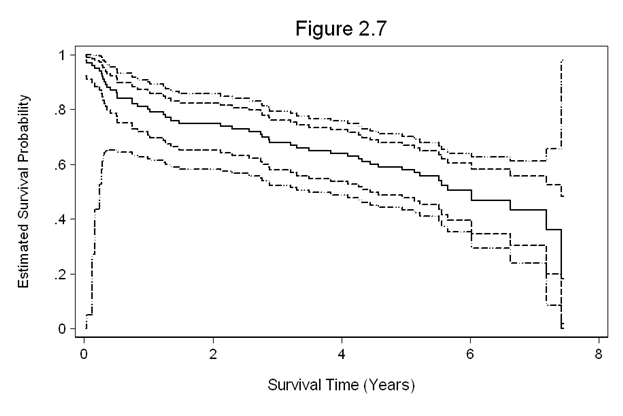
Figure 2.8 on page 35. For this example, we will enter a dataset.
clear
input subject time censor
1 6 1
2 44 1
3 21 0
4 14 1
5 62 1
end
stset time, id(subject) failure(censor)
sts graph, scheme(s2mono) xline(14 44, lpattern(dash)) ///
yline(.25 .5 .75, lpattern(dash)) ///
ylabel(0(.25)1, angle(0)) ///
xlabel(0(12)60) xtitle(Survival Time) ytitle(Estimated Survival Probability) ///
title(Figure 2.8)
failure _d: censor
analysis time _t: time
id: subject
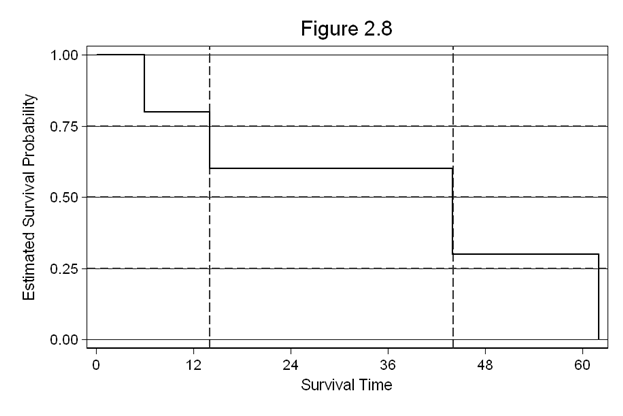
Table 2.5 on page 39. Note that Stata computes the confidence intervals differently from the book.
use https://stats.idre.ucla.edu/stat/examples/asa2/whas100, clear
generate fyear = foltime/365.25
stset fyear, id(id) failure(folstatus)
stsum
failure _d: folstatus
analysis time _t: fyear
id: id
| incidence no. of |------ Survival time -----|
| time at risk rate subjects 25% 50% 75%
---------+---------------------------------------------------------------------
total | 412.156056 .1237395 100 1.472964 6.02601 7.419576
stci
failure _d: folstatus
analysis time _t: fyear
id: id
| no. of
| subjects 50% Std. Err. [95% Conf. Interval]
-------------+-------------------------------------------------------------
total | 100 6.02601 .5603603 4.44627 7.41958
stci, p(25)
failure _d: folstatus
analysis time _t: fyear
id: id
| no. of
| subjects 25% Std. Err. [95% Conf. Interval]
-------------+-------------------------------------------------------------
total | 100 1.472964 .7682197 .750171 3.29911
stci, p(75)
failure _d: folstatus
analysis time _t: fyear
id: id
| no. of
| subjects 75% Std. Err. [95% Conf. Interval]
-------------+-------------------------------------------------------------
total | 100 7.419576 .1409315 7.18412 .
Table 2.6 on page 41. We are using the whas100 dataset from the example above.
sts gen s=s sell=se(lls) sort fyear generate z50 = abs(ln(-ln(s))-ln(-ln(.5)))/sell clist fyear s z50 if z50<1.96 & folstatus==1, noobs
fyear s z50 4.44627 .6 1.909514 4.569473 .59 1.726938 4.944559 .58 1.542441 5.130733 .56884615 1.331001 5.221081 .55674304 1.097873 5.508556 .54036825 .7719651 5.560575 .52348174 .4438371 5.653662 .50478596 .0889862 6.02601 .46872982 .5208178 6.628337 .43267368 1.042136 7.184121 .3605614 1.657685
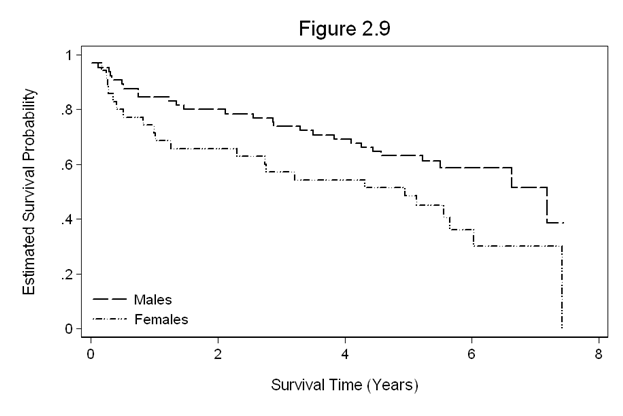
Figure 2.9 on page 46 using the whas100 dataset.
use https://stats.idre.ucla.edu/stat/examples/asa2/whas100.dta, clear gen fyear=foltime/365.25 stset fyear, fail(folstatus) sts gen Sm=s if gender==0 sts gen Sf=s if gender==1 label variable Sm "Estimated Survival Probability (Males)" label variable Sf "Estimated Survival Probability (Females)" sort fyear scatter Sm Sf fyear, ms( none none) c(J J ) yscale(range(0,1)) clpattern(_ ".-." ) /// legend(row(2) col(1) order(1 "Males" 2 "Females") ring(0) position(7)) /// ytitle(Estimated Survival Probability) ylabel(,nogrid angle(horizontal)) /// yscale(titlegap(3)) xtitle(Survival Time (Years)) xscale(titlegap(3)) /// title(Figure 2.9)
Tables 2.9 and 2.10 on page 50. For this example, we enter in the data found in Table 2.9.
clear input time d1 n1 d n 6 0 5 1 9 14 1 5 1 8 44 1 4 1 7 98 1 2 2 4 104 1 1 1 2 114 0 0 1 1 end gen e1 = n1*d/n gen v1 =n1*(n-n1)*d*(n-d)/(n^2*(n-1)) replace v1 = 0 if v1==. gen L = 1 gen W = n gen T = sqrt(n) gen P = (n+1-d)/(n+1) in 1 replace P =P[_n-1]*(n+1-d)/(n+1) in 2/l format e1 v1 L W T P %5.2f list, noobs clean
time d1 n1 d n e1 v1 L W T P
6 0 5 1 9 0.56 0.25 1.00 9.00 3.00 0.90
14 1 5 1 8 0.63 0.23 1.00 8.00 2.83 0.80
44 1 4 1 7 0.57 0.24 1.00 7.00 2.65 0.70
98 1 2 2 4 1.00 0.33 1.00 4.00 2.00 0.42
104 1 1 1 2 0.50 0.25 1.00 2.00 1.41 0.28
114 0 0 1 1 0.00 0.00 1.00 1.00 1.00 0.14
Table 2.11 on page 51 using the data above and the formula (2.21) on page 47 showing how the tests are calculated.
tempvar numerator denominator
gen `numerator' = .
gen `denominator' = .
foreach w of varlist L W T P {
quietly replace `numerator' = `w'*(d1 - e1)
quietly sum `numerator'
local t = (r(sum))^2
quietly replace `denominator' = `w'^2*v1
quietly sum `denominator'
local b = r(sum)
local Q = `t'/`b'
local pvalue =chi2tail(1, `Q')
noisily display "Using weight `w': Q: " %5.2f `Q' " p-value: " %5.2f `pvalue'
}
Using weight L: Q: 0.43 p-value: 0.51 Using weight W: Q: 0.07 p-value: 0.78 Using weight T: Q: 0.20 p-value: 0.66 Using weight P: Q: 0.11 p-value: 0.75
Table 2.12 on page 51 using the whas100 dataset.
use https://stats.idre.ucla.edu/stat/examples/asa2/whas100.dta,clear
gen fyear=foltime/365.25
stset fyear, fail(folstatus)
sts test gender, logrank
failure _d: folstatus
analysis time _t: fyear
Log-rank test for equality of survivor functions
| Events Events
gender | observed expected
-------+-------------------------
0 | 28 34.62
1 | 23 16.38
-------+-------------------------
Total | 51 51.00
chi2(1) = 3.97
Pr>chi2 = 0.0463
sts test gender, wilcoxon
failure _d: folstatus
analysis time _t: fyear
Wilcoxon (Breslow) test for equality of survivor functions
| Events Events Sum of
gender | observed expected ranks
-------+--------------------------------------
0 | 28 34.62 -459
1 | 23 16.38 459
-------+--------------------------------------
Total | 51 51.00 0
chi2(1) = 3.46
Pr>chi2 = 0.0628
sts test gender, tware
failure _d: folstatus
analysis time _t: fyear
Tarone-Ware test for equality of survivor functions
| Events Events Sum of
gender | observed expected ranks
-------+--------------------------------------
0 | 28 34.62 -53.311804
1 | 23 16.38 53.311804
-------+--------------------------------------
Total | 51 51.00 0
chi2(1) = 3.69
Pr>chi2 = 0.0549
sts test gender, peto
failure _d: folstatus
analysis time _t: fyear
Peto-Peto test for equality of survivor functions
| Events Events Sum of
gender | observed expected ranks
-------+--------------------------------------
0 | 28 34.62 -4.9007719
1 | 23 16.38 4.9007719
-------+--------------------------------------
Total | 51 51.00 0
chi2(1) = 3.85
Pr>chi2 = 0.0497
Table 2.13 on page 52 using the whas100 dataset.
recode age 32/59=1 60/69=2 70/79=3 80/92=4, gen(agecat)
(100 differences between age and agecat)
table agecat, cont(freq sum folstatus)
----------------------------------------
RECODE of |
age | Freq. sum(folsta~s)
----------+-----------------------------
1 | 25 8
2 | 23 7
3 | 22 14
4 | 30 22
----------------------------------------
stci, by(agecat) median /* confidence intervals differ from book */
failure _d: folstatus
analysis time _t: fyear
| no. of
agecat | subjects 50% Std. Err. [95% Conf. Interval]
-------------+-------------------------------------------------------------
1 | 25 . . 4.31759 .
2 | 23 7.184121 .0069868 7.18412 .
3 | 22 4.944559 .3229116 .750171 6.62834
4 | 30 2.302532 .9444395 .99384 5.65366
-------------+-------------------------------------------------------------
total | 100 6.02601 .5603603 4.44627 7.41958
Figure 2.10 on page 55 continuing with the whas100 dataset.
sts gen Sage1=s if age<60
sts gen Sage2=s if age>=60 & age<=69
sts gen Sage3=s if age>=70 & age<=79
sts gen Sage4=s if age>=80
preserve
set obs 101
replace fyear = 0 in 101
replace Sage1 = 1 in 101
replace Sage2 = 1 in 101
replace Sage3 = 1 in 101
replace Sage4 = 1 in 101
sort fyear
scatter Sage1 Sage2 Sage3 Sage4 fyear, ms(none none none none) c(J J J J) ylabel(0(0.2)1) ///
clpattern(_ ".-." "-..-" . " -.-") clcolor(black black black black) ///
legend(row(4) col(1) order(1 "Age < 60" 2 "60 <= Age < 69" 3 "70 <= Age < 79" 4 "Age >= 80") ///
ring(0) size(medsmall) pos(7) region(lc(white)) ) graphregion(color(white)) ///
ytitle(Estimated Survival Probability,) ylabel(,nogrid angle(horizontal)) ///
yscale(titlegap(3)) xtitle(Survival Time (Years)) xscale(titlegap(3)) title(Figure 2.10)
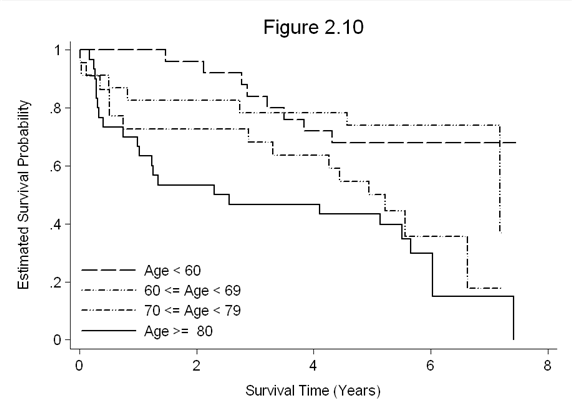
Table 2.15 on page 56 continuing with the whas100 dataset.
restore
sts test agecat, logrank
failure _d: folstatus
analysis time _t: fyear
Log-rank test for equality of survivor functions
| Events Events
agecat | observed expected
-------+-------------------------
1 | 8 15.52
2 | 7 12.92
3 | 14 10.23
4 | 22 12.34
-------+-------------------------
Total | 51 51.00
chi2(3) = 15.57
Pr>chi2 = 0.0014
sts test agecat, wilcoxon
failure _d: folstatus
analysis time _t: fyear
Wilcoxon (Breslow) test for equality of survivor functions
| Events Events Sum of
agecat | observed expected ranks
-------+--------------------------------------
1 | 8 15.52 -490
2 | 7 12.92 -385
3 | 14 10.23 201
4 | 22 12.34 674
-------+--------------------------------------
Total | 51 51.00 0
chi2(3) = 12.30
Pr>chi2 = 0.0064
sts test agecat, tware
failure _d: folstatus
analysis time _t: fyear
Tarone-Ware test for equality of survivor functions
| Events Events Sum of
agecat | observed expected ranks
-------+--------------------------------------
1 | 8 15.52 -56.455489
2 | 7 12.92 -47.843612
3 | 14 10.23 26.687211
4 | 22 12.34 77.611891
-------+--------------------------------------
Total | 51 51.00 0
chi2(3) = 13.52
Pr>chi2 = 0.0036
sts test agecat, peto
failure _d: folstatus
analysis time _t: fyear
Peto-Peto test for equality of survivor functions
| Events Events Sum of
agecat | observed expected ranks
-------+--------------------------------------
1 | 8 15.52 -5.6021925
2 | 7 12.92 -4.0442861
3 | 14 10.23 2.3329794
4 | 22 12.34 7.3134991
-------+--------------------------------------
Total | 51 51.00 0
chi2(3) = 14.54
Pr>chi2 = 0.0023
Table 2.16 on page 57 using the whas100 dataset and the coding scheme defined on page 54.
recode agecat 1=46 2=65 3=75 4 = 86
sts test agecat, logrank trend
failure _d: folstatus
analysis time _t: fyear
Log-rank test for equality of survivor functions
| Events Events
agecat | observed expected
-------+-------------------------
46 | 8 15.52
65 | 7 12.92
75 | 14 10.23
86 | 22 12.34
-------+-------------------------
Total | 51 51.00
chi2(3) = 15.57
Pr>chi2 = 0.0014
Test for trend of survivor functions
chi2(1) = 12.44
Pr>chi2 = 0.0004
sts test agecat, wilcoxon trend
failure _d: folstatus
analysis time _t: fyear
Wilcoxon (Breslow) test for equality of survivor functions
| Events Events Sum of
agecat | observed expected ranks
-------+--------------------------------------
46 | 8 15.52 -490
65 | 7 12.92 -385
75 | 14 10.23 201
86 | 22 12.34 674
-------+--------------------------------------
Total | 51 51.00 0
chi2(3) = 12.30
Pr>chi2 = 0.0064
Test for trend of survivor functions
chi2(1) = 9.99
Pr>chi2 = 0.0016
sts test agecat, tware trend
failure _d: folstatus
analysis time _t: fyear
Tarone-Ware test for equality of survivor functions
| Events Events Sum of
agecat | observed expected ranks
-------+--------------------------------------
46 | 8 15.52 -56.455489
65 | 7 12.92 -47.843612
75 | 14 10.23 26.687211
86 | 22 12.34 77.611891
-------+--------------------------------------
Total | 51 51.00 0
chi2(3) = 13.52
Pr>chi2 = 0.0036
Test for trend of survivor functions
chi2(1) = 10.70
Pr>chi2 = 0.0011
sts test agecat, peto trend
failure _d: folstatus
analysis time _t: fyear
Peto-Peto test for equality of survivor functions
| Events Events Sum of
agecat | observed expected ranks
-------+--------------------------------------
46 | 8 15.52 -5.6021925
65 | 7 12.92 -4.0442861
75 | 14 10.23 2.3329794
86 | 22 12.34 7.3134991
-------+--------------------------------------
Total | 51 51.00 0
chi2(3) = 14.54
Pr>chi2 = 0.0023
Test for trend of survivor functions
chi2(1) = 12.08
Pr>chi2 = 0.0005
Figure 2.11 on page 58 using the bpd dataset.
use https://stats.idre.ucla.edu/stat/examples/asa2/bpd, clear stset ondays, fail(censor) sts gen s0=s if surfact==0 sts gen s1=s if surfact==1 replace s0=1 if s0!=. & ondays==0 replace s1=1 if s1!=. & ondays==0 sts graph, by(surfact) ylabel(0(.2)1) legend( row(2) ring(0) position(1)) /// xtitle(Days on Oxygen) ytitle(Estimated Aurvival Probability) /// ylabel(, nogrid) title(Figure 2.11)
Table 2.17 on page 58 using the bpd dataset.
sts test suf, logrank
failure _d: censor
analysis time _t: days
Log-rank test for equality of survivor functions
| Events Events
suf | observed expected
------+-------------------------
0 | 40 48.95
1 | 33 24.05
------+-------------------------
Total | 73 73.00
chi2(1) = 5.62
Pr>chi2 = 0.0178
sts test suf, wilcoxon
failure _d: censor
analysis time _t: days
Wilcoxon (Breslow) test for equality of survivor functions
| Events Events Sum of
suf | observed expected ranks
------+--------------------------------------
0 | 40 48.95 -310
1 | 33 24.05 310
------+--------------------------------------
Total | 73 73.00 0
chi2(1) = 2.49
Pr>chi2 = 0.1146
sts test suf, tware
failure _d: censor
analysis time _t: days
Tarone-Ware test for equality of survivor functions
| Events Events Sum of
suf | observed expected ranks
------+--------------------------------------
0 | 40 48.95 -50.779103
1 | 33 24.05 50.779103
------+--------------------------------------
Total | 73 73.00 0
chi2(1) = 3.70
Pr>chi2 = 0.0545
sts test suf, peto
failure _d: censor
analysis time _t: days
Peto-Peto test for equality of survivor functions
| Events Events Sum of
suf | observed expected ranks
------+--------------------------------------
0 | 40 48.95 -3.9371075
1 | 33 24.05 3.9371075
------+--------------------------------------
Total | 73 73.00 0
chi2(1) = 2.53
Pr>chi2 = 0.1114
Figure 2.12 on page 61 using the whas100 dataset.
use https://stats.idre.ucla.edu/stat/examples/asa2/whas100.dta, clear gen fyear = foltime/365.25 stset fyear, fail(folstatus) sts gen skm=s sna=na snalb=lb(na) snaub=ub(na) skmlb=lb(s) skmub=ub(s) replace sna=exp(-sna) replace snaub=exp(-snaub) replace snalb=exp(-snalb) twoway line sna snalb skm skmlb snaub skmub fyear, sort c(J J J J J J) yscale(range(0,1)) /// clpattern(. ".-." - "..-.." ".-." "..-..") /// legend(row(2) col(2) /// order(1 "Nelson-Aalen" 2 "N-A Limits" 3 "Kaplan-Meier" 4 "K-M Limits") /// ring(0) size(medsmall) pos(7) region(lc(white)) ) graphregion(color(white)) /// ytitle(Estimated Survival Probability) ylabel(,nogrid angle(horizontal)) /// yscale(titlegap(3)) xscale(titlegap(3)) xtitle(Survival time (Years)) /// title(Figure 2.12)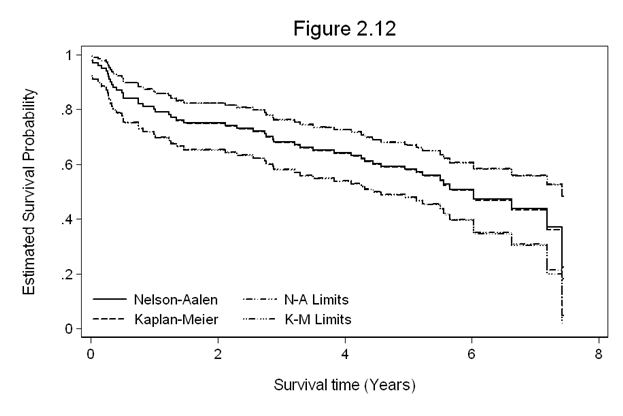
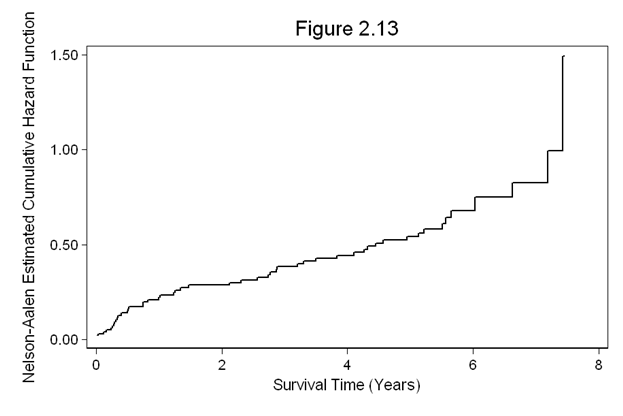
Figure 2.13 on page 62 using the whas100 dataset.sts graph, cumhaz ytitle(Nelson-Aalen Estimated Cumulative Hazard Function) /// xtitle(Survival Time (Years)) ylabel(,nogrid) title(Figure 2.13)
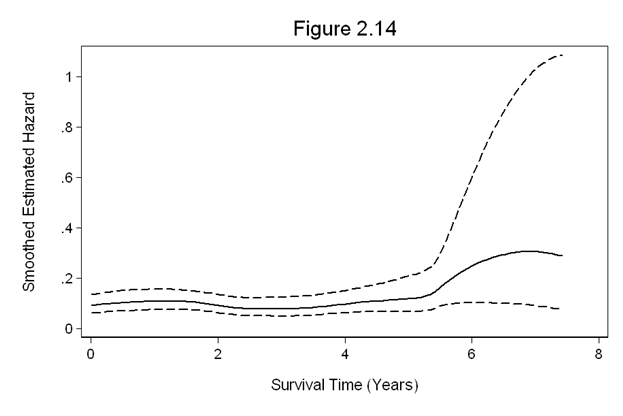
Figure 2.14 on page 64 using the whas100 dataset.
use https://stats.idre.ucla.edu/stat/examples/asa2/whas100.dta, clear gen fyear = foltime/365.25 stset fyear, fail(folstatus) sts graph, hazard cih title(Figure 2.14) xtitle(Survival Time (Years)) /// ytitle("Smoothed Estimated Hazard") ylabel(0(.2)1, nogrid angle(horizontal)) /// yscale(titlegap(3)) xscale(titlegap(3)) noboundary /// legend (off) ciopts(lpattern(dash) lcolor(black) fcolor(none))