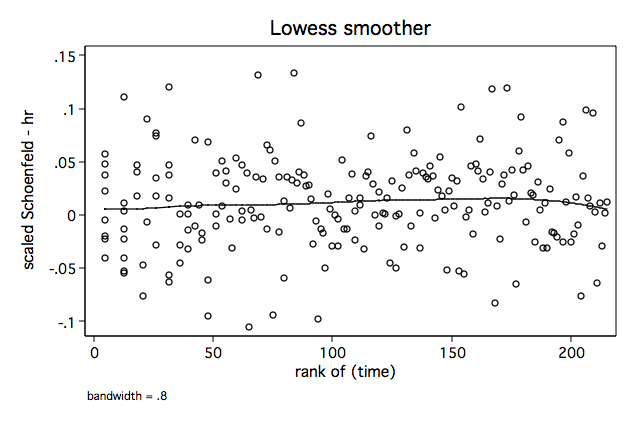
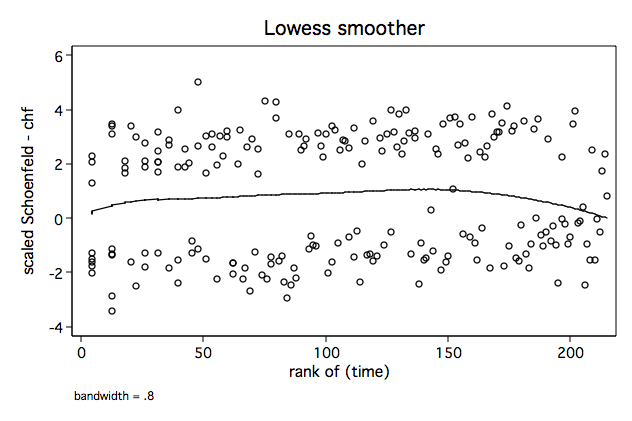
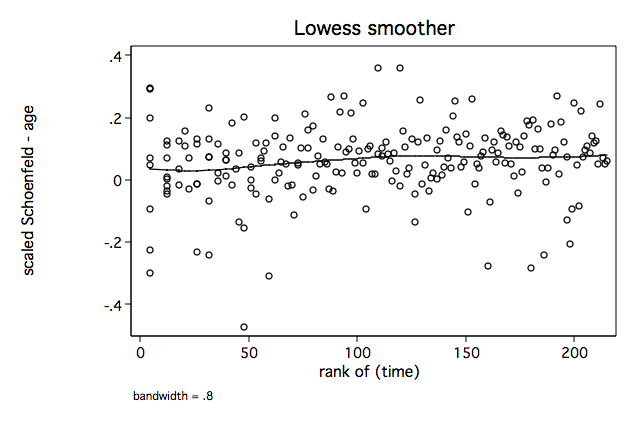
Table 6.1 on page 180 using the whas500 data. To generate the score tests and global tests in this table, we will first run a Cox regression with the indicated variables. Then we can indicate the various tests.
use https://stats.idre.ucla.edu/stat/examples/asa2/whas500, clear
generate time = lenfol/365.25
stset time, fail(fstat)
generate bmifp1=(bmi/10)^2
generate bmifp2=(bmi/10)^3
generate ga = gender*age
stcox bmifp1 bmifp2 age hr diasbp gender chf ga, ///
nolog nohr mgale(mgale) bases(S0) sch(sch*) sca(sca*) esr(scr*)
failure _d: fstat
analysis time _t: time
Cox regression -- Breslow method for ties
No. of subjects = 500 Number of obs = 500
No. of failures = 215
Time at risk = 1207.989046
LR chi2(8) = 222.60
Log likelihood = -1116.2793 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
_t | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
bmifp1 | -.6730201 .1735831 -3.88 0.000 -1.013237 -.3328035
bmifp2 | .1421257 .0394413 3.60 0.000 .0648222 .2194292
age | .0605347 .0083175 7.28 0.000 .0442327 .0768367
hr | .0116719 .0029427 3.97 0.000 .0059044 .0174394
diasbp | -.0107119 .0034741 -3.08 0.002 -.017521 -.0039027
gender | 1.855257 .9578425 1.94 0.053 -.0220801 3.732594
chf | .823524 .1465418 5.62 0.000 .5363074 1.110741
ga | -.0276658 .0120503 -2.30 0.022 -.051284 -.0040476
------------------------------------------------------------------------------
estat phtest, detail /* g(t) = t */
Test of proportional-hazards assumption
Time: Time
----------------------------------------------------------------
| rho chi2 df Prob>chi2
------------+---------------------------------------------------
bmifp1 | 0.08343 1.66 1 0.1979
bmifp2 | -0.07232 1.24 1 0.2652
age | 0.08347 1.41 1 0.2356
hr | 0.01913 0.08 1 0.7765
diasbp | 0.00023 0.00 1 0.9972
gender | 0.03404 0.23 1 0.6304
chf | -0.04372 0.44 1 0.5068
ga | -0.02981 0.18 1 0.6724
------------+---------------------------------------------------
global test | 3.65 8 0.8869
----------------------------------------------------------------
estat phtest, log detail /* g(t) = ln(t) */
Test of proportional-hazards assumption
Time: Log(t)
----------------------------------------------------------------
| rho chi2 df Prob>chi2
------------+---------------------------------------------------
bmifp1 | 0.00699 0.01 1 0.9141
bmifp2 | 0.00352 0.00 1 0.9567
age | 0.14584 4.29 1 0.0382
hr | 0.06847 1.03 1 0.3098
diasbp | 0.04669 0.53 1 0.4667
gender | 0.10119 2.05 1 0.1526
chf | 0.03799 0.33 1 0.5640
ga | -0.10549 2.24 1 0.1345
------------+---------------------------------------------------
global test | 7.47 8 0.4869
----------------------------------------------------------------
estat phtest, km detail /* g(t) = Skm(t) */
Test of proportional-hazards assumption
Time: Kaplan-Meier
----------------------------------------------------------------
| rho chi2 df Prob>chi2
------------+---------------------------------------------------
bmifp1 | 0.03835 0.35 1 0.5540
bmifp2 | -0.02760 0.18 1 0.6706
age | 0.12766 3.29 1 0.0697
hr | 0.05075 0.57 1 0.4516
diasbp | 0.03786 0.35 1 0.5550
gender | 0.08120 1.32 1 0.2511
chf | 0.01055 0.03 1 0.8727
ga | -0.08196 1.35 1 0.2449
------------+---------------------------------------------------
global test | 5.10 8 0.7466
----------------------------------------------------------------
estat phtest, rank detail /* g(t) = rank(t) */
Test of proportional-hazards assumption
Time: Rank(t)
----------------------------------------------------------------
| rho chi2 df Prob>chi2
------------+---------------------------------------------------
bmifp1 | 0.02681 0.17 1 0.6791
bmifp2 | -0.01530 0.06 1 0.8136
age | 0.13833 3.86 1 0.0493
hr | 0.06433 0.91 1 0.3399
diasbp | 0.04099 0.41 1 0.5228
gender | 0.09077 1.65 1 0.1995
chf | 0.01952 0.09 1 0.7669
ga | -0.09258 1.73 1 0.1890
------------+---------------------------------------------------
global test | 6.36 8 0.6072
----------------------------------------------------------------
Figure 6.1 on page 181 continuing to use the whas500 data.
sts gen skm = s generate ln_t=ln(time) /* Figure 6.1a */ lowess sca4 ln_t, name(fig6_1a, replace)/* Figure 6.1b */ lowess sca4 _t, name(fig6_1b, replace)
/* Figure 6.1c */ lowess sca4 skm, name(fig6_1c, replace)
/* Figure 6.1d */ egen rank_t=rank(time) if fstat==1 lowess sca4 rank_t, name(fig6_1d, replace)
Figure 6.2 on page 182 continuing to use the whas500 data.
/* Figure 6.2a */ lowess sca7 ln_t, name(fig6_2a, replace)/* Figure 6.2b */ lowess sca7 _t, name(fig6_2b, replace)
/* Figure 6.2c */ lowess sca7 skm, name(fig6_2c, replace)
/* Figure 6.2d */ lowess sca7 rank_t, name(fig6_2d, replace)
Figure 6.3 on page 183 continuing to use the whas500 data.
/* Figure 6.3a */ lowess sca3 ln_t, name(fig6_3a, replace)/* Figure 6.3b */ lowess sca3 _t, name(fig6_3b, replace)
/* Figure 6.3c */ lowess sca3 skm, name(fig6_3c, replace)
/* Figure 6.3d */ lowess sca3 rank_t, name(fig6_3d, replace)
Figure 6.4 on page 186 continuing to use the whas500 data.
/* Figure 6.4a */ twoway scatter scr1 bmi, name(fig6_4a, replace)/* Figure 6.4b */ twoway scatter scr2 bmi, name(fig6_4b, replace)
/* Figure 6.4c */ twoway scatter scr4 hr, name(fig6_4c, replace)
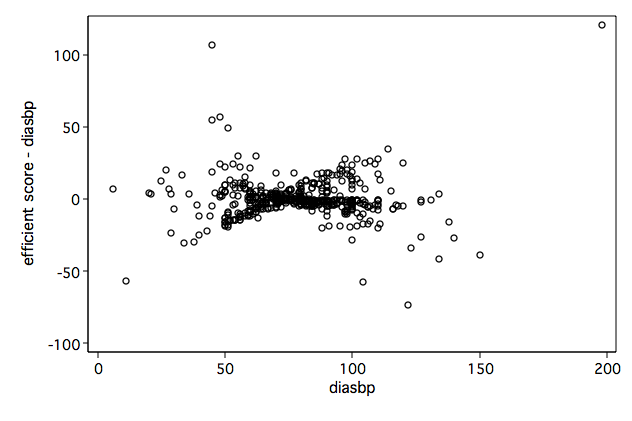
/* Figure 6.4d */ twoway scatter scr5 diasbp, name(fig6_4d, replace)
Figure 6.5 on page 186 continuing to use the whas500 data.
/* Figure 6.5a */ twoway scatter scr3 age, name(fig6_5a, replace)/* Figure 6.5b */ twoway scatter scr8 ga if ga~=0, name(fig6_5b, replace) /// ylabel(-200(100)200) xlabel(20(20)100)
/* Figure 6.5c */ graph box scr7, over(chf) name(fig6_5c, replace)
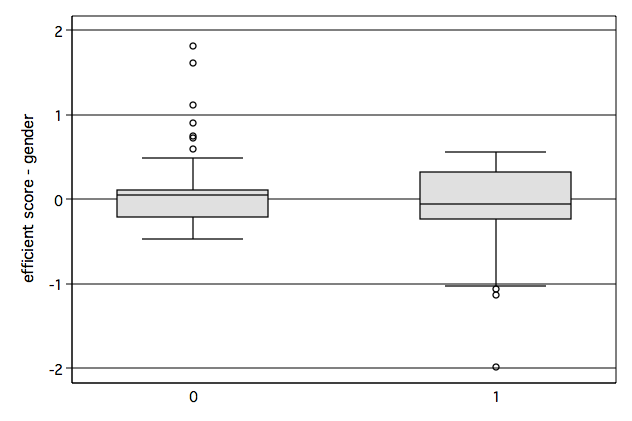
/* Figure 6.5d */ graph box scr6, over(gender) name(fig6_5d, replace)
Figure 6.6 on page 187 continuing to use the whas500 data. We will be using the variance-covariance matrix of the estimators from the Cox regression run above.
/* compute scaled score residuals */ set matsize 600 mat V = e(V) mkmat scr1 scr2 scr3 scr4 scr5 scr6 scr7 scr8, mat(L) matrix DB = L*V svmat DB, name(db) /* Figure 6.6a */ twoway scatter db1 bmi, name(fig6_6a, replace)/* Figure 6.6b */ twoway scatter db2 bmi, name(fig6_6b, replace)
/* Figure 6.6c */ twoway scatter db4 hr, name(fig6_6c, replace)
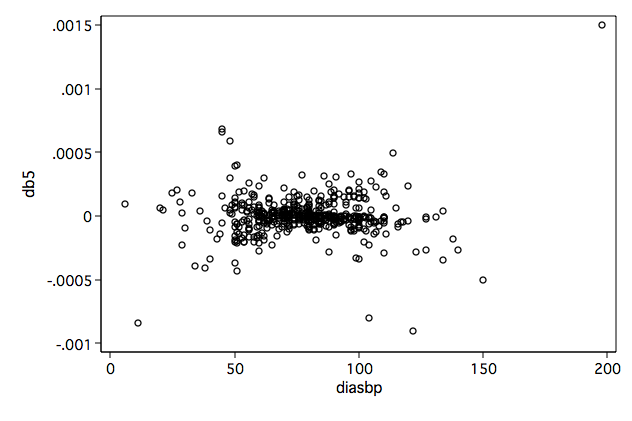
/* Figure 6.6d */ twoway scatter db5 diasbp, name(fig6_6d, replace)
Figure 6.7 on page 188 continuing to use the whas500 data.
/* Figure 6.7a */ twoway scatter db3 age, name(fig6_7a, replace)/* Figure 6.7b */ twoway scatter db8 ga if ga~=0, name(fig6_7b, replace) /// ylabel(-.004(.002).004) xlabel(20(20)100)
/* Figure 6.7c */ graph box db7, over(chf) name(fig6_7c, replace)
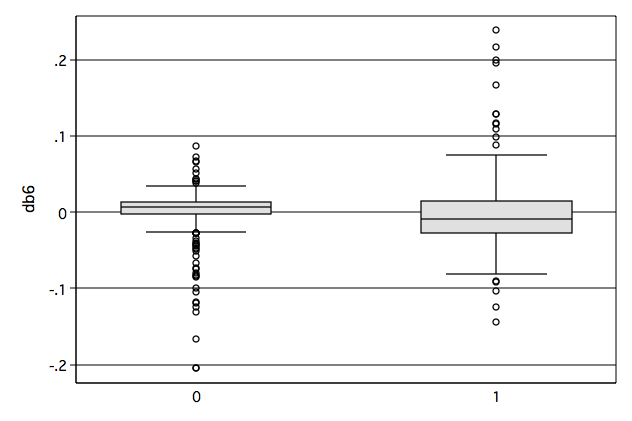
/* Figure 6.7d */ graph box db6, over(gender) name(fig6_7d, replace)
Figure 6.8 on page 190 continuing to use the whas500 data. We first calculate the likelihood displacement and then plot this against the Martingale residuals. We are presenting this example before Table 6.2 on page 189 because the points highlighted in this figure in the text are incorporated into the table.
/* compute likelihood displacement values */
forvalues i=1/8 {
generate ld`i' = scr`i'*db`i'
}
generate ld = ld1+ld2+ld3+ld4+ld5+ld6+ld7+ld8
twoway scatter ld mgale, xtitle(Martingale Residuals) ytitle(Likelihood Displacement)
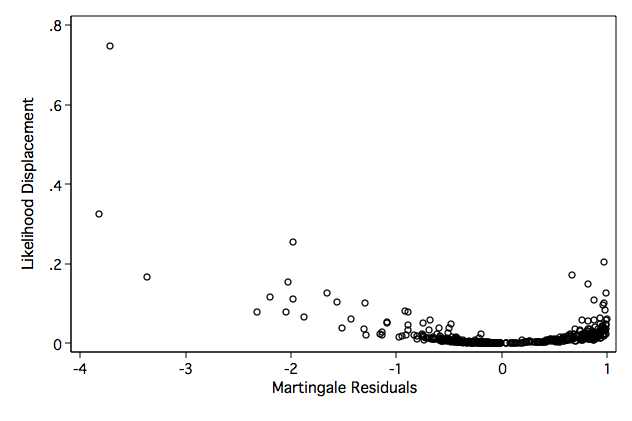
Table 6.2 on page 189 continuing to use the whas500 data. In the text, the authors highlighted points in Figures 6.4-6.8 that appeared to be points with high leverage, high influence, or large Cook’s distance. The points listed below correspond to these highlighted points.
list id bmi age hr diasbp gender chf ///
if inlist(id,51,89,112,115,153,194,251,256,416,472), ///
noobs sep(0)
+----------------------------------------------------+
| id bmi age hr diasbp gender chf |
|----------------------------------------------------|
| 51 22.44662 80 105 72 0 1 |
| 89 15.92695 95 62 45 0 0 |
| 112 14.84283 87 105 104 1 0 |
| 115 18.90242 81 118 70 1 1 |
| 153 39.93835 32 102 83 1 0 |
| 194 24.21079 43 47 90 0 1 |
| 251 22.27393 102 89 60 0 1 |
| 256 44.83886 53 96 99 1 0 |
| 416 28.55371 80 64 198 0 0 |
| 472 25.40431 72 186 84 0 0 |
+----------------------------------------------------+
This set of points was arrived at using the following code to identify the highlighted observations in the figures.
* Listing of subjects identified in Figure 6.4 list id bmi scr1 if bmi < 20& scr1>8 list id bmi scr2 if bmi < 20& scr2>20 list id hr scr4 if scr4>90 list id diasbp scr5 if scr5>100 * Listing of subjects identified in Figure 6.5 list id age scr3 if age>80& scr3<-50 list id age scr8 if age>80& scr8<-150 list id chf scr7 if chf==0 & scr7>1.5 list id chf scr7 if chf==1 & scr7<-1.5 list id gender scr6 if gender==0 & scr6>1.5 list id gender scr6 if gender==1 & scr6<-1.5 * Listing of subjects identified in Figure 6.6 list id bmi db1 if bmi < 20& db1 >0.05 list id bmi db2 if bmi<20 & db2<-0.01 list id bmi db2 if bmi >41 & db2>0.01 list id hr db4 if hr>170 list id diasbp db5 if diasbp>190 * Listing of subjects identified in Figure 6.7 list id age db3 if age>85& db3<-0.002 list id age db8 if age<40 & db8 <-0.002 list id age db8 if age>70 & db8 >0.002 list id chf db7 if chf==1 & db7<-0.03 list id gender db6 if gender==0 & db6<-.15 * Listing of subjects identified in Figure 6.8 list id mgale ld if mgale<-3 &ld>.2
Table 6.3 on age 191 continuing to use the whas500 data.
stcox bmifp1 bmifp2 age hr diasbp gender chf ga if id~=416, nohr nolog
failure _d: fstat
analysis time _t: time
Cox regression -- Breslow method for ties
No. of subjects = 499 Number of obs = 499
No. of failures = 214
Time at risk = 1207.671455
LR chi2(8) = 225.90
Log likelihood = -1108.4149 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
_t | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
bmifp1 | -.685039 .1740807 -3.94 0.000 -1.026231 -.343847
bmifp2 | .1447858 .039543 3.66 0.000 .0672829 .2222888
age | .0595811 .008329 7.15 0.000 .0432565 .0759057
hr | .0121705 .0029455 4.13 0.000 .0063975 .0179435
diasbp | -.0122364 .0035128 -3.48 0.000 -.0191215 -.0053514
gender | 1.838366 .9579476 1.92 0.055 -.0391769 3.715909
chf | .8302922 .1469312 5.65 0.000 .5423124 1.118272
ga | -.0274281 .0120524 -2.28 0.023 -.0510503 -.0038059
------------------------------------------------------------------------------
Table 6.4 on page 194 continuing to use the whas500 data. You can download stcoxgof by typing search stcoxgof and following the instructions. Slight differences in the division of the dataset into quintiles results in slight differences between the results below and the table in the text.
drop mgale
quietly stcox bmifp1 bmifp2 age hr diasbp gender chf ga if diasbp~=198, ///
nohr nolog mgale(mgale)
stcoxgof
Goodness-of-fit test for the inclusion of design variables based on 5 quantiles of risk
(Added variables version of the Groennesby and Borgan test)
Score test chi2(4) = 9.354
Prob > chi2 = 0.0528
Likelihood-ratio test LR chi2(4) = 9.786
Prob > chi2 = 0.0442
(Table collapsed on quantiles of linear predictor)
--------------------------------------------------------------------------------
Quantile |
of Risk | Observed Expected z p-Norm Observations
----------+---------------------------------------------------------------------
1 | 6 8.169 -.759 .448 100
2 | 15 22.471 -1.576 .115 100
3 | 40 37.213 .457 .648 99
4 | 66 53.599 1.694 .09 100
5 | 87 92.549 -.577 .564 100
|
Total | 214 214 499
--------------------------------------------------------------------------------
Table 6.5 on page 196 continuing to use the whas500 data.
drop if id==416
stcox bmifp1 bmifp2 age hr diasbp gender chf ga, nohr nolog
failure _d: fstat
analysis time _t: time
Cox regression -- Breslow method for ties
No. of subjects = 499 Number of obs = 499
No. of failures = 214
Time at risk = 1207.671455
LR chi2(8) = 225.90
Log likelihood = -1108.4149 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
_t | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
bmifp1 | -.685039 .1740807 -3.94 0.000 -1.026231 -.343847
bmifp2 | .1447858 .039543 3.66 0.000 .0672829 .2222888
age | .0595811 .008329 7.15 0.000 .0432565 .0759057
hr | .0121705 .0029455 4.13 0.000 .0063975 .0179435
diasbp | -.0122364 .0035128 -3.48 0.000 -.0191215 -.0053514
gender | 1.838366 .9579476 1.92 0.055 -.0391769 3.715909
chf | .8302922 .1469312 5.65 0.000 .5423124 1.118272
ga | -.0274281 .0120524 -2.28 0.023 -.0510503 -.0038059
------------------------------------------------------------------------------
Table 6.6 on page 197 continuing to use the whas500 data.
lincom _b[hr]*10, hr
( 1) 10 hr = 0
------------------------------------------------------------------------------
_t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | 1.129421 .0332666 4.13 0.000 1.066065 1.196541
------------------------------------------------------------------------------
lincom _b[diasbp]*10, hr
( 1) 10 diasbp = 0
------------------------------------------------------------------------------
_t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | .8848258 .0310824 -3.48 0.000 .8259553 .9478924
------------------------------------------------------------------------------
lincom _b[chf], hr
( 1) chf = 0
------------------------------------------------------------------------------
_t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | 2.293989 .3370585 5.65 0.000 1.719979 3.059563
------------------------------------------------------------------------------
Table 6.7 on page 198 continuing to use the whas500 data.
/* for coefficients */
display exp(1.838-0.027*40)
2.1340039
display exp(1.838-0.027*50)
1.6290548
display exp(1.838-0.027*60)
1.2435871
display exp(1.838-0.027*70)
.94932887
display exp(1.838-0.027*80)
.72469819
display exp(1.838-0.027*90)
.55321974
/* for confidence intervals */
lincom _b[gender]+_b[ga]*40, hr
( 1) gender + 40 ga = 0
------------------------------------------------------------------------------
_t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | 2.098539 1.0209 1.52 0.128 .8087675 5.445159
------------------------------------------------------------------------------
lincom _b[gender]+_b[ga]*50, hr
( 1) gender + 50 ga = 0
------------------------------------------------------------------------------
_t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | 1.595138 .5948045 1.25 0.210 .768064 3.312832
------------------------------------------------------------------------------
lincom _b[gender]+_b[ga]*60, hr
( 1) gender + 60 ga = 0
------------------------------------------------------------------------------
_t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | 1.212494 .3218842 0.73 0.468 .7206241 2.040095
------------------------------------------------------------------------------
lincom _b[gender]+_b[ga]*70, hr
( 1) gender + 70 ga = 0
------------------------------------------------------------------------------
_t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | .9216391 .1621659 -0.46 0.643 .6528129 1.301167
------------------------------------------------------------------------------
lincom _b[gender]+_b[ga]*80, hr
( 1) gender + 80 ga = 0
------------------------------------------------------------------------------
_t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | .7005548 .1002935 -2.49 0.013 .5291534 .9274761
------------------------------------------------------------------------------
lincom _b[gender]+_b[ga]*90, hr
( 1) gender + 90 ga = 0
------------------------------------------------------------------------------
_t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | .5325046 .1052738 -3.19 0.001 .361447 .7845166
------------------------------------------------------------------------------
Figure 6.9 on page 202 continuing to use the whas500 data.
drop S0
quietly stcox bmifp1 bmifp2 age hr diasbp gender chf ga if id ~= 416, ///
nolog nohr bases(S0)
matrix v=e(V)
generate a = bmifp1-9.9225
generate b=bmifp2-31.25588
generate ln_HR=_b[bmifp1]*a+_b[bmifp2]*b
generate HR=exp(ln_HR)
generate SE_ln_HR=sqrt(a^2*v[1,1]+b^2*v[2,2]+2*a*b*v[2,1])
generate ln_HR_l = ln_HR-1.96*SE_ln_HR
generate ln_HR_u= ln_HR+1.96*SE_ln_HR
generate HR_l=exp(ln_HR_l)
generate HR_u=exp(ln_HR_u)
generate one=1
line HR HR_l HR_u one bmi if HR_u<=10, sort clpattern(solid shortdash shortdash ".") ///
legend(row(2) col(1) pos(12) ///
order(1 "Estimated Hazard Ratio" 2 "Confidence limits") ///
ring(0) size(small) region(lc(white))) ylabel(0 1 2 4 6 8, nogrid) ///
ytitle("Estimated Hazard Ratio") yscale(titlegap(3)) ///
xscale(titlegap(3) ) lc(black) graphregion(fcolor(white))
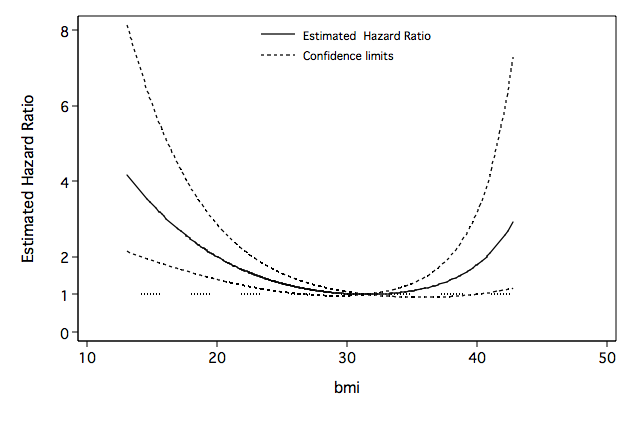
Table 6.8 on page 203 continuing to use the whas500 data.
display (15/10)^2-9.9225
-7.6725
display (15/10)^3-31.25588
-27.88088
lincom _b[bmifp1]*(-7.6725)+_b[bmifp2]*(-27.88088), hr
( 1) - 7.6725 bmifp1 - 27.88088 bmifp2 = 0
------------------------------------------------------------------------------
_t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | 3.384496 .997724 4.14 0.000 1.89918 6.031451
------------------------------------------------------------------------------
display (20/10)^2-9.9225
-5.9225
display (20/10)^3-31.25588
-23.25588
lincom _b[bmifp1]*(-5.9225)+_b[bmifp2]*(-23.25588), hr
( 1) - 5.9225 bmifp1 - 23.25588 bmifp2 = 0
------------------------------------------------------------------------------
_t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | 1.993758 .364173 3.78 0.000 1.393782 2.852003
------------------------------------------------------------------------------
display (25/10)^2-9.9225
-3.6725
display (25/10)^3-31.25588
-15.63088
lincom _b[bmifp1]*(-3.6725)+_b[bmifp2]*(-15.63088), hr
( 1) - 3.6725 bmifp1 - 15.63088 bmifp2 = 0
------------------------------------------------------------------------------
_t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | 1.287465 .1233862 2.64 0.008 1.066988 1.553502
------------------------------------------------------------------------------
display (30/10)^2-9.9225
-.9225
display (30/10)^3-31.25588
-4.25588
lincom _b[bmifp1]*(-0.9255)+_b[bmifp2]*(-4.25588), hr
( 1) - .9255 bmifp1 - 4.25588 bmifp2 = 0
------------------------------------------------------------------------------
_t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | 1.017972 .0259702 0.70 0.485 .968323 1.070167
------------------------------------------------------------------------------
display (35/10)^2-9.9225
2.3275
display (35/10)^3-31.25588
11.61912
lincom _b[bmifp1]*(2.3275)+_b[bmifp2]*(11.61912), hr
( 1) 2.3275 bmifp1 + 11.61912 bmifp2 = 0
------------------------------------------------------------------------------
_t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | 1.091831 .0917488 1.05 0.296 .9260343 1.287311
------------------------------------------------------------------------------
display (40/10)^2-9.9225
6.0775
display (40/10)^3-31.25588
32.74412
lincom _b[bmifp1]*(6.0775)+_b[bmifp2]*(32.74412), hr
( 1) 6.0775 bmifp1 + 32.74412 bmifp2 = 0
------------------------------------------------------------------------------
_t | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
(1) | 1.781687 .5236036 1.97 0.049 1.001566 3.169445
------------------------------------------------------------------------------
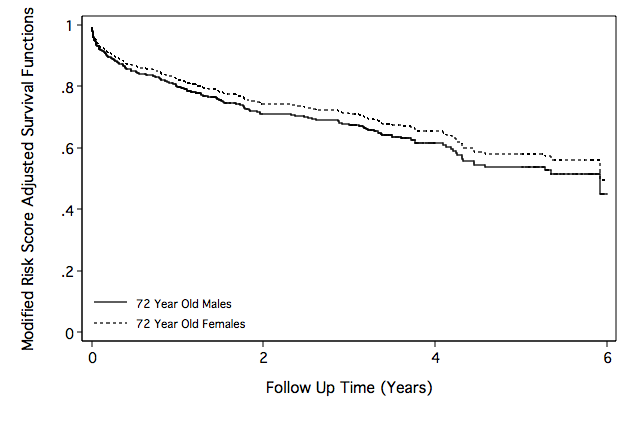
Figure 6.10 on page 204 continuing to use the whas500 data.
drop S0
quietly stcox bmifp1 bmifp2 age hr diasbp gender chf ga if id ~= 416, ///
nolog nohr bases(S0)
predict r,xb
generate rm=r-_b[age]*age-_b[gender]*gender-_b[ga]*age*gender
quietly summarize rm, detail
display r(p50)
-1.7518661
generate S_m72=S0^(exp(r(p50)+_b[age]*72))
generate S_f72=S0^(exp(r(p50)+_b[age]*72+_b[gender]+_b[ga]*72))
line S_m72 S_f72 time if id~=416 & time < 6, c(J J) sort ///
clpattern(solid shortdash) ///
legend(row(2) col(1) pos(7) ///
order(1 "72 Year Old Males" 2 "72 Year Old Females") ///
ring(0) size(small) region(lc(white))) ylabel(0(0.2)1, nogrid) ///
ytitle("Modified Risk Score Adjusted Survival Functions") ///
yscale(titlegap(3)) xscale(titlegap(3) ) ///
lc(black) graphregion(fcolor(white)) xtitle("Follow Up Time (Years)")