All of the examples in this chapter use the whas100 data.
use https://stats.idre.ucla.edu/stat/examples/asa2/whas100, clear
Table 8.1 on page 250.
generate time=foltime/365.25
stset time, fail(folstatus)
streg gender, dist(exp) nolog nohr time
failure _d: folstatus
analysis time _t: time
Exponential regression -- accelerated failure-time form
No. of subjects = 100 Number of obs = 100
No. of failures = 51
Time at risk = 412.156056
LR chi2(1) = 4.42
Log likelihood = -145.12583 Prob > chi2 = 0.0356
------------------------------------------------------------------------------
_t | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gender | -.6016208 .2814117 -2.14 0.033 -1.153178 -.050064
_cons | 2.317579 .1889822 12.26 0.000 1.947181 2.687978
------------------------------------------------------------------------------
Table 8.2 on page 252.
generate ga = gender*age
streg gender age ga bmi, dist(exp) nolog nohr time
failure _d: folstatus
analysis time _t: time
Exponential regression -- accelerated failure-time form
No. of subjects = 100 Number of obs = 100
No. of failures = 51
Time at risk = 412.156056
LR chi2(4) = 28.25
Log likelihood = -133.20784 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
_t | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gender | -3.932349 1.809825 -2.17 0.030 -7.479541 -.3851573
age | -.0531945 .0157007 -3.39 0.001 -.0839674 -.0224216
ga | .0497528 .0241489 2.06 0.039 .0024218 .0970838
bmi | .0934975 .0375579 2.49 0.013 .0198854 .1671095
_cons | 3.389083 1.619997 2.09 0.036 .2139474 6.56422
------------------------------------------------------------------------------
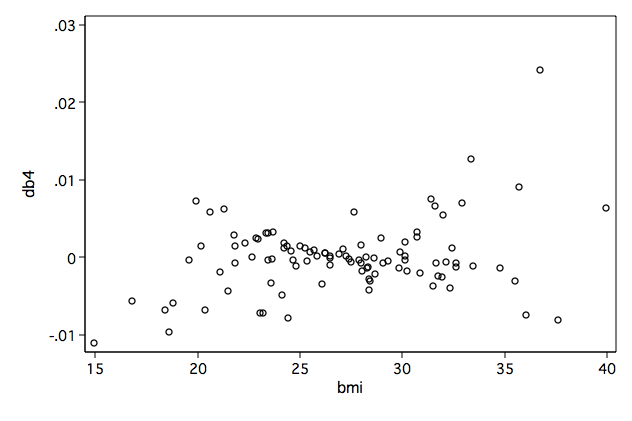
Figure 8.1a-d on page 255 using the variance-covariance matrix generated by the model above.
/* compute scaled score residuals */ mat V = e(V) predict mgale, mgale generate l1 = -gender*mgale generate l2 = -age*mgale generate l3 = -ga*mgale generate l4 = -bmi*mgale generate l5 = -1*mgale mkmat l1 l2 l3 l4 l5, mat(L) matrix DB = L*V svmat DB, name(db) /* 8.1a */ graph box db1, over(gender) name(fig8_1a, replace)/* 8.1b */ graph twoway scatter db2 age, name(fig8_1b, replace)
/* 8.1c */ graph twoway scatter db3 age if gender, name(fig8_1c, replace)
/* 8.1d */ graph twoway scatter db4 bmi, name(fig8_1d, replace)
Figure 8.2 on page 256 using the model from an above example.
/* compute likelihood displacement values */
forvalues i=1/5 {
generate ld`i' = l`i'*db`i'
}
generate ld = ld1+ld2+ld3+ld4+ld5twoway (scatter ld mgale if ~folstatus)(scatter ld mgale if folstatus), ///
legend(order(1 "Non-censored" 2 "Censored") pos(11) ring(0) ) ///
name(fig8_2, replace)
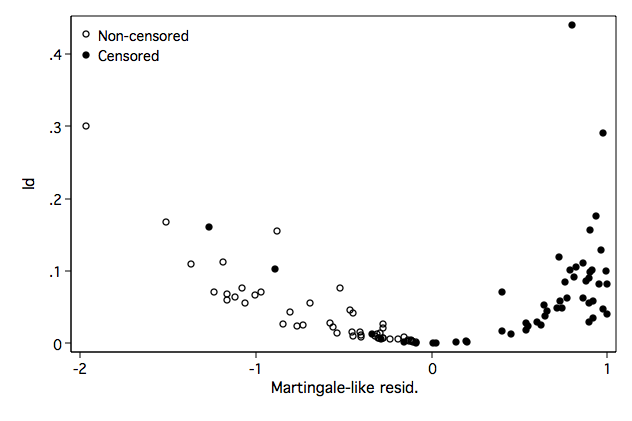
Table 8.3 on page 256. We first identify the observations that appear highlighted in Figures 8.1 and 8.2 and then generate the table.
list id if ((gender== 1 & db1 <-.5) | /// (age > 80 & db2 < -.003) | /// (age > 80 & db2 > .004) | /// (age < 60 & db3 > .004) | /// (bmi > 35 & db4 < -.010) | /// (ld > .25)), noobs sep(0) +----+ | id | |----| | 30 | | 52 | | 58 | | 61 | | 93 | | 97 | +----+ list id gender age bmi if inlist(id, 30, 52, 58, 61, 93, 97), noobs sep(0) +------------------------------+ | id gender age bmi | |------------------------------| | 30 1 85 36.71647 | | 52 1 43 25.33148 | | 58 0 92 24.3664 | | 61 0 90 24.78423 | | 93 1 80 20.59809 | | 97 1 32 39.93835 | +------------------------------+
Figure 8.3 on page 258 using predicted values from the model from an above example.
predict hex, cs
stset hex, fail(folstatus)
sts gen skm=s
generate hkm=-ln(skm)
line hex hkm hex ,sort clpattern(solid shortdash) legend(off) ylabel(, nogrid) ///
ytitle("Kaplan-Meier Estimated Cumulative Hazard") yscale(titlegap(3)) xscale(titlegap(3) ) ///
lc(black) graphregion(fcolor(white)) name(fig8_3, replace) ///
xtitle("Exponential Regression Model Cumulative Hazard")
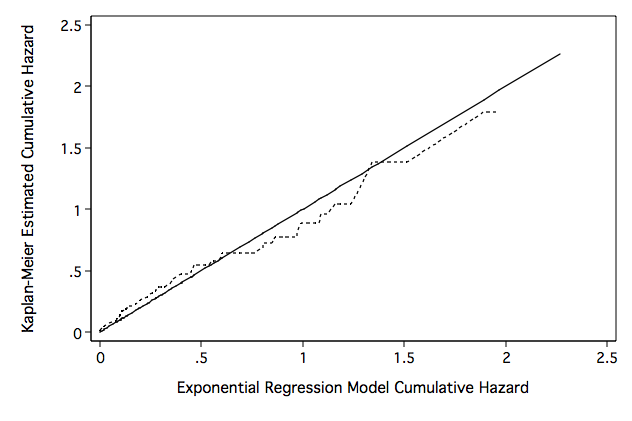
Table 8.4 on page 259 using the predicted values from the model above. The results shown here differ from those given in the book.
predict xb, xb
predict cs, cs
sort xb
global nd2 = _N/2
global nd21 = $nd2 + 1
generate grp=1 in 1/$nd2
replace grp=2 in $nd21/l
table grp, cont(sum folstatus sum cs)
----------------------------------------
grp | sum(folsta~s) sum(cs)
----------+-----------------------------
1 | 33 9.157227
2 | 18 .9968994
----------------------------------------
/* z-scores for Table 8.4 */
display (33-37.27436)/sqrt(37.27436)
-.70010955
display (18-13.72565)/sqrt(13.72565)
1.1537285
drop mgale-grp
Table 8.5 on page 264.
quietly stset time, fail(folstatus)
streg gender age ga bmi, dist(weib) nolog nohr time
failure _d: folstatus
analysis time _t: time
Weibull regression -- accelerated failure-time form
No. of subjects = 100 Number of obs = 100
No. of failures = 51
Time at risk = 412.156056
LR chi2(4) = 25.36
Log likelihood = -131.4099 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
_t | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gender | -4.68945 2.284832 -2.05 0.040 -9.167638 -.2112628
age | -.0639403 .0206278 -3.10 0.002 -.1043699 -.0235106
ga | .0591542 .0304218 1.94 0.052 -.0004713 .1187798
bmi | .1055103 .0464755 2.27 0.023 .0144199 .1966007
_cons | 3.9721 2.047007 1.94 0.052 -.0399612 7.984161
-------------+----------------------------------------------------------------
/ln_p | -.22544 .1242178 -1.81 0.070 -.4689025 .0180225
-------------+----------------------------------------------------------------
p | .7981649 .0991463 .6256886 1.018186
1/p | 1.252874 .1556293 .982139 1.598239
------------------------------------------------------------------------------
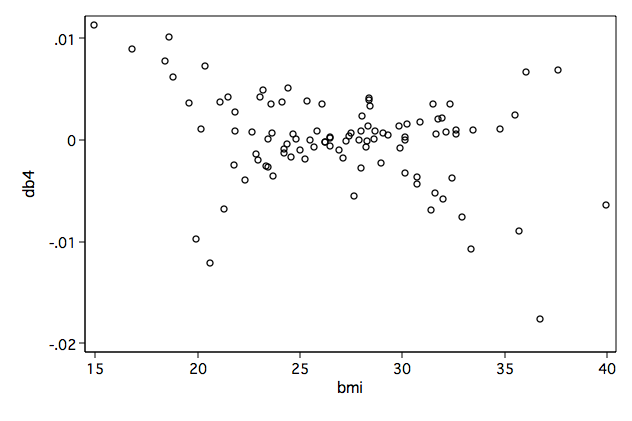
Figure 8.4a-d on page 266.
/* compute scaled score residulas */ mat V = e(V) predict double mgale, mgale predict xb, xb generate l1 = -gender/1.252874*mgale generate l2 = -age/1.252874*mgale generate l3 = -ga/1.252874*mgale generate l4 = -bmi/1.252874*mgale generate l5 = -mgale/1.252874 generate zhat = 1/1.252874*(ln(_t)-xb) generate l6 = folstatus+zhat*(folstatus-exp(zhat)) mkmat l1 l2 l3 l4 l5 l6, mat(L) matrix DB = L*V svmat DB, name(db) /* 8.4a */ graph box db1, over(gender) name(fig8_4a, replace)/* 8.4b */ graph twoway scatter db2 age, ylabel(-.004(.002).006) name(fig8_4b, replace)
/* 8.4c */ graph twoway scatter db3 age if gender, name(fig8_4c, replace)
/* 8.4d */ graph twoway scatter db4 bmi, name(fig8_4d, replace)
Figure 8.5 on page 267.
graph box db6, name(fig8_5, replace)
Table 8.6 on page 267. We first identify the observations that appear highlighted in Figures 8.4, 8.5 and 8.6 and then generate the table.
/* compute likelihood displacement values */
forvalues i=1/6 {
generate ld`i' = l`i'*db`i'
}
generate ld = ld1+ld2+ld3+ld4+ld5+ld6
list id if ((db6 < -.05) | ///
(db1 < -0.6) | ///
(db2 < -.004 & age > 80) | ///
(db2 > .005 & age > 80) | ///
(db3 > .004 & age < 50) | ///
(db4 < -0.015 & bmi > 35)| ///
(db6 < -.05)| ///
(mgale < -1 & ld > .2)| ///
(mgale > .5 & ld > .3)), noobs sep(0)
+----+
| id |
|----|
| 58 |
| 61 |
| 93 |
| 52 |
| 31 |
| 30 |
| 1 |
| 97 |
+----+
sort id
list id gender age bmi if inlist(id, 1, 30, 31, 52, 58, 61, 93, 97), noobs sep(0)
+------------------------------+
| id gender age bmi |
|------------------------------|
| 1 0 65 31.38134 |
| 30 1 85 36.71647 |
| 31 0 72 27.97907 |
| 52 1 43 25.33148 |
| 58 0 92 24.3664 |
| 61 0 90 24.78423 |
| 93 1 80 20.59809 |
| 97 1 32 39.93835 |
+------------------------------+
Figure 8.6 on page 268.
twoway (scatter ld mgale if ~folstatus)(scatter ld mgale if folstatus), ///
legend(order(1 "Censored" 2 "Non-censored") pos(11) ring(0) ) ///
name(fig8_6, replace)
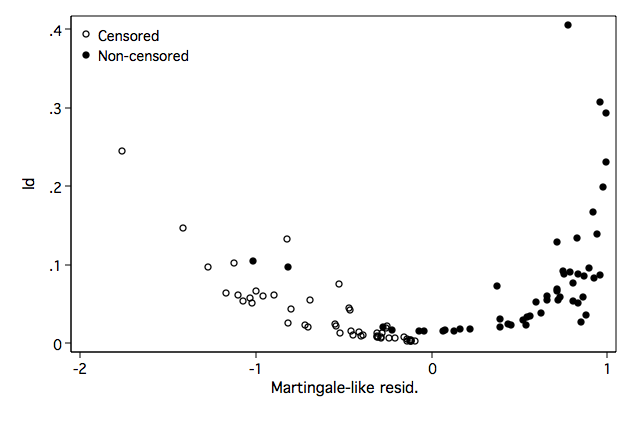
Figure 8.7 on page 269.
quietly stset time, fail(folstatus)
quietly streg gender age ga bmi, dist(weib) nohr time nolog
predict hwb,cs
stset hwb, fail(folstatus)
sts gen skm=S
generate hkm=-ln(skm)
line hwb hkm hwb, sort clpattern(solid shortdash) legend(off) ///
ytitle("Kaplan-Meier Estimated Cumulative Hazard") ///
xtitle("Weibull Regression Model Cumulative Hazard") name(fig8_7, replace)
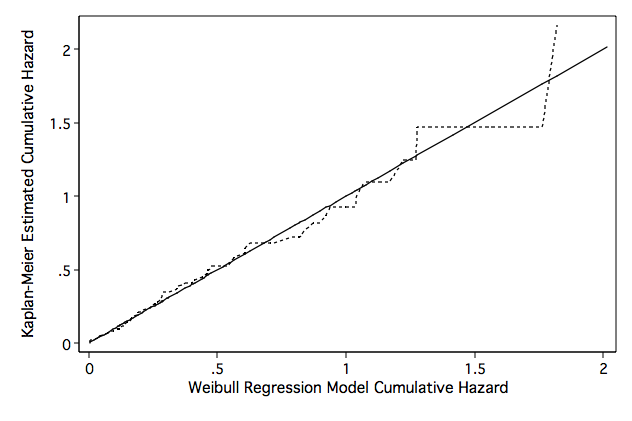
Table 8.7 on page 270.
drop xb
predict xb, xb
predict cs, cs
sort xb
global nd2 = _N/2
global nd21 = $nd2 + 1
generate grp=1 in 1/$nd2
replace grp=2 in $nd21/l
table grp, cont(sum folstatus sum cs)
----------------------------------------
grp | sum(folsta~s) sum(cs)
----------+-----------------------------
1 | 33 12.29835
2 | 18 1.739923
----------------------------------------
/* z-scores for Table 8.7 */
display (33-36.96986)/sqrt(36.96986)
-.65290695
display (18-14.03015)/sqrt(14.03015)
1.0598464
Figure 8.8 on page 271.
generate age_c=age-70
generate bmi_c=bmi-27
generate ga_c=gender*age_c
quietly stset time, fail(folstatus)
quietly streg gender age_c ga_c bmi_c , d(exp) nohr time nolog
generate he_t=exp(-_b[_cons])
quietly streg gender age_c ga_c bmi_c , d(weib) nohr time nolog
scalar sigma=exp(-[ln_p]_b[_cons])
generate hw_t=(1/sigma)*(exp(-[_t]_b[_cons]/sigma))*(time^((1/sigma)-1))
line he_t hw_t time, sort c(l l) clpattern(solid shortdash) ylabel(, nogrid angle(horizontal)) ///
ytitle(" Estimated Hazard Function") yscale(titlegap(3)) xscale(titlegap(3) ) ///
lc(black black) graphregion(fcolor(white)) xtitle("Follow Up Time (Years)") ///
legend( order(1 "Exponential Hazard" 2 "Weibull Hazard") pos(12) row(2) col(1) ring(0) ///
region(lc(white))) name(fig8_8, replace)
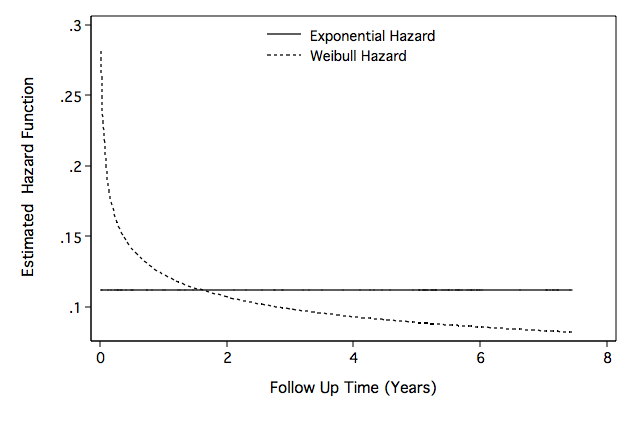
Figure 8.9 on page 272.
quietly streg gender age ga bmi , d(weib) nohr time nolog
generate rm70=3.972-4.689*0-0.064*70+0.059*0*70+0.106*27
generate Sm70=exp((-time^(1/1.253))*exp(-rm/1.253))
generate rf70=3.972-4.689*1-0.064*70+0.059*1*70+0.106*27
generate Sf70=exp((-time^(1/1.253))*exp(-rf/1.253))
line Sm70 Sf70 time, sort c(J J) clpattern(solid shortdash) ///
ylabel(, nogrid angle(horizontal)) ytitle(" Estimated Survival Function") ///
yscale(titlegap(3)) xscale(titlegap(3) ) lc(black black) ///
graphregion(fcolor(white)) xtitle("Follow Up Time (Years)") ///
legend( order(1 "Males" 2 "Females") pos(7) row(2) col(1) ring(0) ///
region(lc(white))) ylabel(0(.2)1) name(fig8_9, replace)
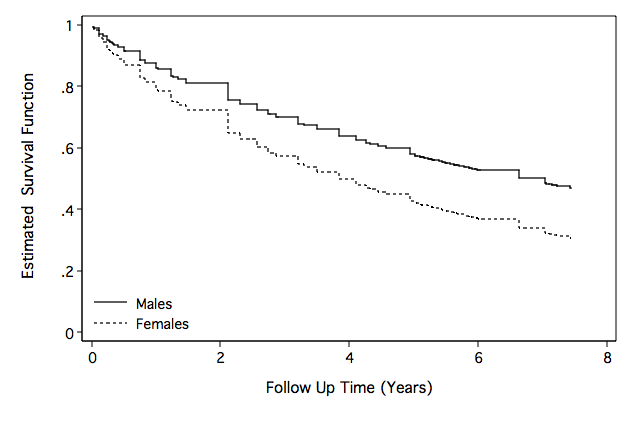drop mgale-Sf70
Table 8.8 on page 277.
quietly stset time, fail(folstatus)
streg gender age ga bmi, dist(logl) time nolog
failure _d: folstatus
analysis time _t: time
Loglogistic regression -- accelerated failure-time form
No. of subjects = 100 Number of obs = 100
No. of failures = 51
Time at risk = 412.156056
LR chi2(4) = 24.65
Log likelihood = -132.88256 Prob > chi2 = 0.0001
------------------------------------------------------------------------------
_t | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
gender | -4.694876 2.29155 -2.05 0.040 -9.186232 -.2035205
age | -.0650646 .0210013 -3.10 0.002 -.1062264 -.0239027
ga | .0586938 .0312761 1.88 0.061 -.0026061 .1199938
bmi | .110001 .0457745 2.40 0.016 .0202846 .1997175
_cons | 3.467881 2.026041 1.71 0.087 -.5030863 7.438849
-------------+----------------------------------------------------------------
/ln_gam | .0411854 .1210114 0.34 0.734 -.1959925 .2783634
-------------+----------------------------------------------------------------
gamma | 1.042045 .1260993 .8220184 1.320966
------------------------------------------------------------------------------
Figure 8.10 on page 278.
predict mgale, mgale
generate age_c=age-70
generate bmi_c=bmi-27
generate gac=gender*age_c
quietly streg gender age_c gac bmi_c, d(logl) time
generate t_model=(1/1.042045)*exp(-1.883391/1.042045)*(_t^((1/1.042045)-1))/ ///
(1+exp(-1.883391/1.042045)*(_t^(1/1.042045)))
generate t_125=(1/1.25)*exp(-1.883391/1.25)*(_t^((1/1.25)-1))/ ///
(1+exp(-1.883391/1.25)*(_t^(1/1.25)))
generate t_5=(1/0.5)*exp(-1.883391/0.5)*(_t^((1/0.5)-1))/ ///
(1+exp(-1.883391/0.5)*(_t^(1/0.5)))
generate t_25=(1/0.25)*exp(-1.883391/0.25)*(_t^((1/0.25)-1))/ ///
(1+exp(-1.883391/0.25)*(_t^(1/0.25)))
line t_model t_125 t_5 t_25 t_model time, ///
sort clpattern(solid longdash "-##" "..#-#" ) ///
lc(black black black black black) lw(thin thin thin thin) ///
ytitle("Log Logistic Hazard") legend( row(4) col(1) pos(12) ///
order( 1 "Fitted Model" 2 "Sigma = 1.25" 3 "Sigma = 0.5" 4 "Sigma = 0.25") ///
region(lc(white)) size(small) ring(0)) xtitle("Survival Time (Years)") ///
ylabel(,nogrid angle(horizontal)) yscale(titlegap(3)) ///
graphregion(fcolor(white)) xscale(titlegap(3)) name(fig8_10, replace)
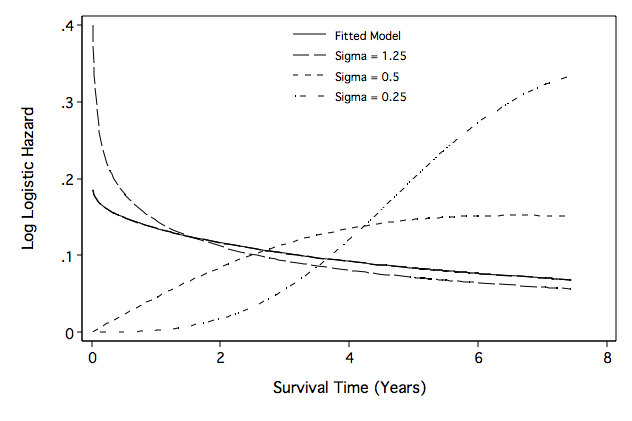drop mgale
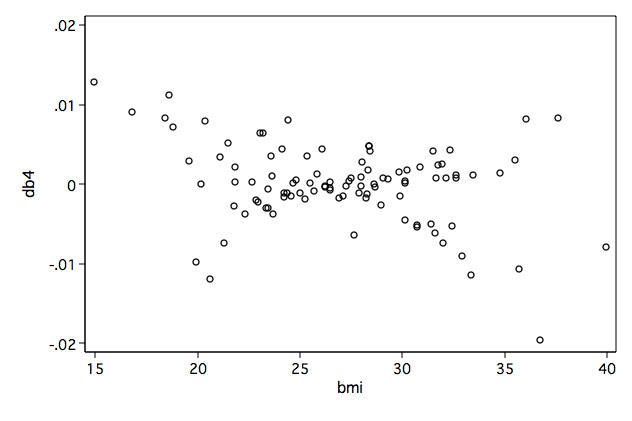
Figure 8.11a-d on page 279.
/* compute scaled score residulas */ mat V = e(V) predict double mgale, mgale predict xb, xb global gamma = exp(_b[ln_gam:_cons]) generate zhat = (ln(_t)-xb)/($gamma) generate cpart = folstatus-(1+folstatus)*(exp(zhat)/(1+exp(zhat))) generate l1 = gender/$gamma*cpart generate l2 = age/$gamma*cpart generate l3 = ga/$gamma*cpart generate l4 = bmi/$gamma*cpart generate l5 = 1/$gamma*cpart generate l6 = folstatus+zhat*cpart mkmat l1 l2 l3 l4 l5 l6, mat(L) matrix DB = L*V svmat DB, name(db) /* 8.11a */ graph box db1, over(gender) name(fig8_11a, replace)/* 8.11b */ graph twoway scatter db2 age, name(fig8_11b, replace)
/* 8.11c */ graph twoway scatter db3 age if gender, name(fig8_11c, replace)
/* 8.11d */ graph twoway scatter db4 bmi, name(fig8_11d, replace)
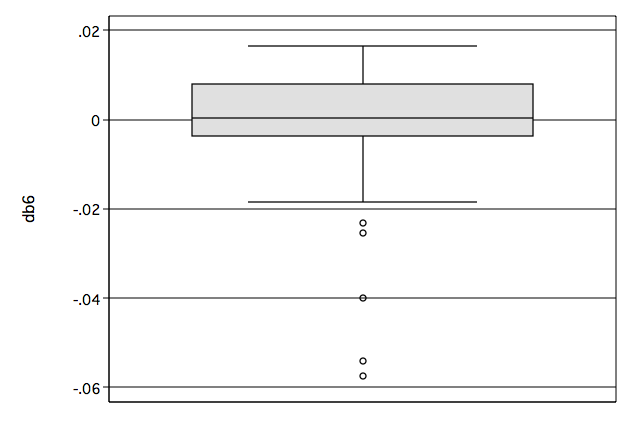
Figure 8.12 on page 280.
graph box db6, name(fig8_12, replace)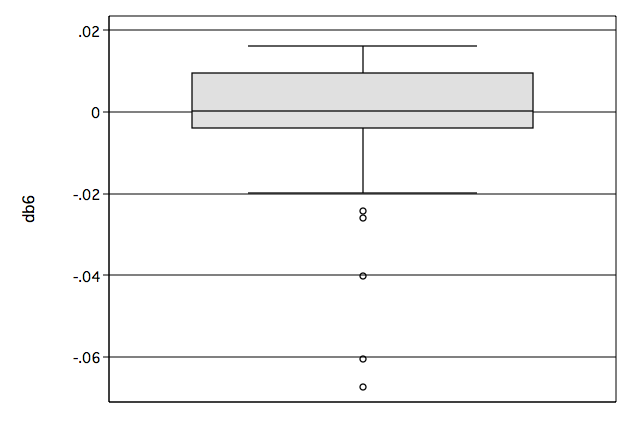
Table 8.9 on page 281.We first identify the observations that appear highlighted in Figures 8.11, 8.12 and 8.13 and then generate the table.
forvalues i=1/5 {
generate ld`i' = l`i'*db`i'
}
generate ld = ld1+ld2+ld3+ld4+ld5
list id if ((gender == 0 & db1 < -.5) | ///
(gender == 1 & db1 > .5) | ///
(db2 < -.006) | ///
(db3 < -.01) | ///
(db4 > .02)| ///
(db6 < -.06)| ///
(mgale < .8 & ld > .3)| ///
(mgale > .9 & ld > .45)), noobs sep(0)
+----+
| id |
|----|
| 56 |
| 31 |
| 30 |
| 1 |
| 97 |
| 67 |
+----+
sort id
list id gender age bmi if inlist(id, 1, 30, 31, 56, 67, 97), noobs sep(0)
+------------------------------+
| id gender age bmi |
|------------------------------|
| 1 0 65 31.38134 |
| 30 1 85 36.71647 |
| 31 0 72 27.97907 |
| 56 1 64 24.41255 |
| 67 0 48 31.58373 |
| 97 1 32 39.93835 |
+------------------------------+
Figure 8.13 on page 281.
twoway (scatter ld mgale if ~folstatus)(scatter ld mgale if folstatus), ///
legend(order(1 "Non-censored" 2 "Censored") pos(11) ring(0) ) ///
name(fig8_13, replace)
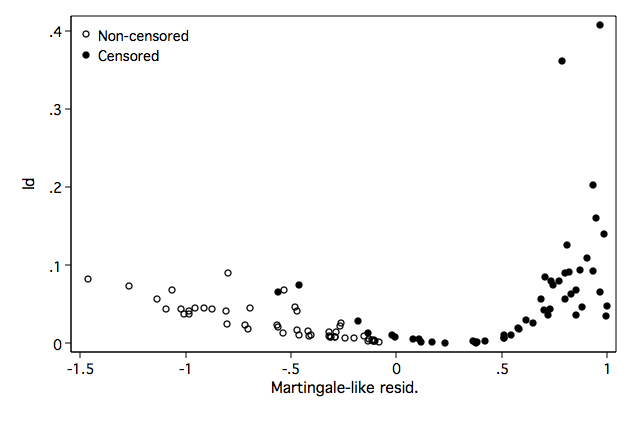
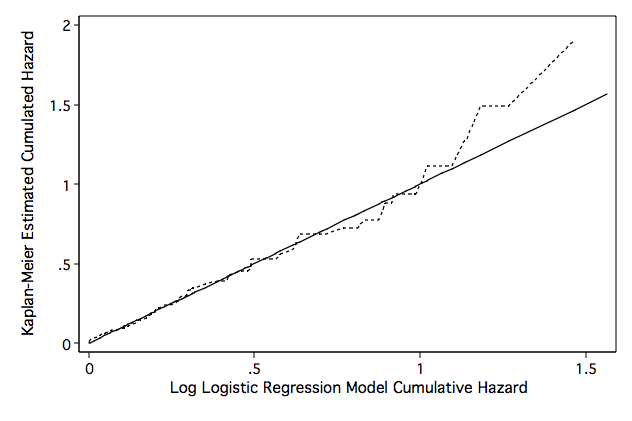
Figure 8.14 on page 282
quietly stset time, fail(folstatus)
quietly streg gender age ga bmi, dist(logl) time nolog
predict hwb,cs
stset hwb, fail(folstatus)
sts gen skm=S
generate hkm=-ln(skm)
line hwb hkm hwb, sort clpattern(solid shortdash) legend(off) ///
ytitle("Kaplan-Meier Estimated Cumulated Hazard") ///
xtitle("Log Logistic Regression Model Cumulative Hazard") name(fig8_14, replace)
