Part of table 12.1, page 323. The variable index corresponds to the row value in table 12.1.
use https://stats.idre.ucla.edu/stat/stata/examples/chp/p323, clear
generate index = _n
list in f/5
y x1 x2 x3 index
1. 0 -62.8 -89.5 1.7 1
2. 0 3.3 -3.5 1.1 2
3. 0 -120.8 -103.2 2.5 3
4. 0 -18.1 -28.8 1.1 4
5. 0 -3.8 -50.6 .9 5
list in -5/l
y x1 x2 x3 index
62. 1 53.1 7.1 1.9 62
63. 1 39.8 13.8 1.2 63
64. 1 59.5 7 2 64
65. 1 16.3 20.4 1 65
66. 1 21.7 -7.8 1.6 66
Page 324, table 12.2.
Note: The first logit command displays the results as coefficients while the second logit command with the or option displays the results as odds ratios.
logit y x1 x2 x3
Logit estimates Number of obs = 66
LR chi2(3) = 85.68
Prob > chi2 = 0.0000
Log likelihood = -2.9064524 Pseudo R2 = 0.9365
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
x1 | .3312468 .3007071 1.102 0.271 -.2581284 .9206219
x2 | .1808756 .1069197 1.692 0.091 -.0286831 .3904344
x3 | 5.087464 5.081626 1.001 0.317 -4.87234 15.04727
_cons | -10.15345 10.8389 -0.937 0.349 -31.3973 11.0904
------------------------------------------------------------------------------
Note: 17 failures and 10 successes completely determined.
logit, or
Logit estimates Number of obs = 66
LR chi2(3) = 85.68
Prob > chi2 = 0.0000
Log likelihood = -2.9064524 Pseudo R2 = 0.9365
------------------------------------------------------------------------------
y | Odds Ratio Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
x1 | 1.392703 .4187958 1.102 0.271 .7724961 2.510851
x2 | 1.198266 .1281183 1.692 0.091 .9717243 1.477623
x3 | 161.9786 823.1147 1.001 0.317 .0076554 3427251
------------------------------------------------------------------------------
Note: 17 failures and 10 successes completely determined.
Logistic regression diagnostics, page 325.
predict p /* predicted probabilities */ predict pr, rstandard /* standardized Personian residuals */ (10 missing values generated) predict dr, deviance /* deviance residuals */ predict pstar, hat /* leverage */ predict dbeta, dbeta /* DBETA */ (10 missing values generated) predict dg, dx2 /* change in chi-square when observation deleted */ (10 missing values generated)
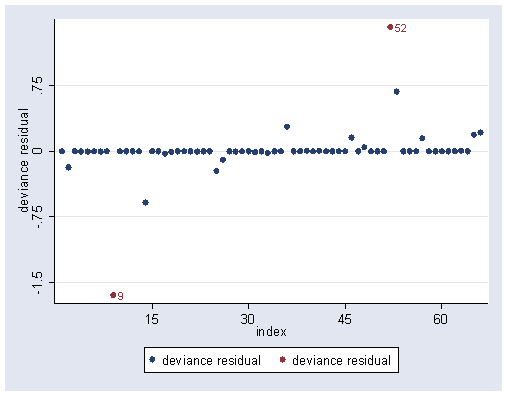
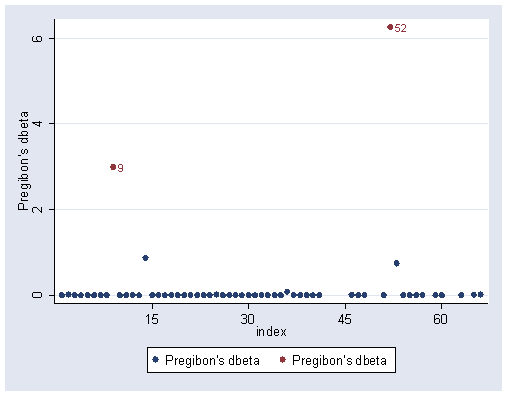
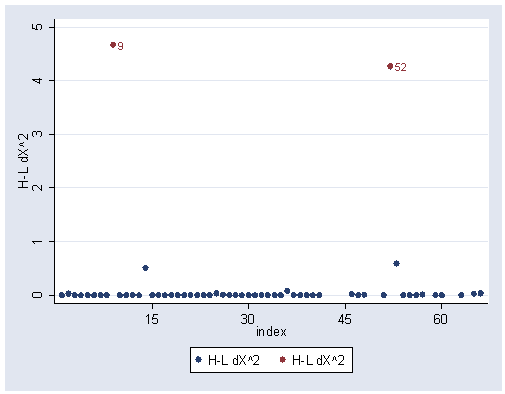
Figures 12.2, 12.3 and 12.4, pages 326 and 327.
Note: Observations 9 and 52 appear to be problematic; however, observation 36 does not appear problematic, differing from the figures in the book.
sort index graph twoway (scatter dr index) (scatter dr index if abs(dr) >= 1, mlabel(index)), /// ylabel(-1.5(.75).75) xlabel(15(15)60)
graph twoway (scatter dbeta index) (scatter dbeta index if abs(dbeta) >= 2, mlabel(index)), /// xlabel(15(15)60)
graph twoway (scatter dg index) (scatter dg index if abs(dg) >= 2, mlabel(index)), /// xlabel(15(15)60)
Likelihood ratio test, page 327 and table 12.3, page 328.
lrtest, saving (0)
logit y x1 x2
Logit estimates Number of obs = 66
LR chi2(2) = 82.02
Prob > chi2 = 0.0000
Log likelihood = -4.7359473 Pseudo R2 = 0.8965
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
x1 | .1573639 .0749183 2.100 0.036 .0105267 .3042011
x2 | .1947428 .1224281 1.591 0.112 -.0452119 .4346974
_cons | -.5503398 .9509818 -0.579 0.563 -2.41423 1.31355
------------------------------------------------------------------------------
Note: 11 failures and 0 successes completely determined.
lrtest
Logit: likelihood-ratio test chi2(1) = 3.66
Prob > chi2 = 0.0558
Likelihood ratio test, page 328 and table 12.4, page 328.
lrtest, saving(1)
logit y x1
Logit estimates Number of obs = 66
LR chi2(1) = 75.69
Prob > chi2 = 0.0000
Log likelihood = -7.9015445 Pseudo R2 = 0.8273
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
x1 | .1767191 .0571025 3.095 0.002 .0648004 .2886379
_cons | -1.166587 .8163989 -1.429 0.153 -2.7667 .4335252
------------------------------------------------------------------------------
Note: 9 failures and 0 successes completely determined.
lrtest, using(1)
Logit: likelihood-ratio test chi2(1) = 6.33
Prob > chi2 = 0.0119
Table 12.5, page 331.
regress y x1 x2 x3
Source | SS df MS Number of obs = 66
---------+------------------------------ F( 3, 62) = 27.38
Model | 9.40333712 3 3.13444571 Prob > F = 0.0000
Residual | 7.09666288 62 .114462305 R-squared = 0.5699
---------+------------------------------ Adj R-squared = 0.5491
Total | 16.50 65 .253846154 Root MSE = .33832
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
x1 | .0031216 .0008294 3.764 0.000 .0014637 .0047795
x2 | .0042457 .0014367 2.955 0.004 .0013737 .0071177
x3 | .1485037 .0453154 3.277 0.002 .0579195 .2390878
_cons | .3218658 .0874576 3.680 0.000 .1470407 .496691
------------------------------------------------------------------------------
Table 12.6, page 332.
Note: the command generate a = p >= .5 creates a new variable a which has the value 1 if p is greater or equal to .5 and 0 otherwise.
predict p
generate a = p >= .5
list y p a
y p a
1. 0 -.0017021 0
2. 0 .4806612 0
3. 0 -.122117 0
4. 0 .3064435 0
5. 0 .2288255 0
6. 0 .1446737 0
7. 0 .3331264 0
8. 0 -.320569 0
9. 0 .517042 1
10. 0 .1161951 0
11. 0 .2255089 0
12. 0 -.0724799 0
13. 0 -.8029544 0
14. 0 .545396 1
15. 0 .0301355 0
16. 0 -.4522537 0
17. 0 .6364052 1
18. 0 .4545762 0
19. 0 .437882 0
20. 0 .1398092 0
21. 0 .2249177 0
22. 0 .3714215 0
23. 0 .1800966 0
24. 0 .0519476 0
25. 0 .5541553 1
26. 0 .5563999 1
27. 0 .394581 0
28. 0 .3399023 0
29. 0 .3882431 0
30. 0 .262901 0
31. 0 .3894134 0
32. 0 .117767 0
33. 0 .4403123 0
34. 1 .7187779 1
35. 1 .8186681 1
36. 1 .7295072 1
37. 1 .8015884 1
38. 1 .6547927 1
39. 1 .7962746 1
40. 1 .7478317 1
41. 1 .7593519 1
42. 1 .8322027 1
43. 1 1.099869 1
44. 1 1.420885 1
45. 1 .8599006 1
46. 1 .657912 1
47. 1 .8058342 1
48. 1 .5835429 1
49. 1 .9690604 1
50. 1 1.029698 1
51. 1 .7686977 1
52. 1 .4763457 0
53. 1 .5957797 1
54. 1 .7405336 1
55. 1 .8092653 1
56. 1 .8389035 1
57. 1 .6227317 1
58. 1 .8070596 1
59. 1 .7396857 1
60. 1 .843024 1
61. 1 .8565065 1
62. 1 .7999232 1
63. 1 .6828997 1
64. 1 .8343272 1
65. 1 .6078632 1
66. 1 .5940937 1