Note: The generate command is used to add an id number to the observations.
use https://stats.idre.ucla.edu/stat/stata/examples/chp/p124 generate id = _n
Table 5.1, page 124.
list
s x e m
1. 13876 1 1 1
2. 11608 1 3 0
3. 18701 1 3 1
4. 11283 1 2 0
5. 11767 1 3 0
6. 20872 2 2 1
7. 11772 2 2 0
8. 10535 2 1 0
9. 12195 2 3 0
10. 12313 3 2 0
..
[remainder of output omitted]
Create dummy coding for variable e.
Note 1: tabulate with the generate option creates dummy coded variables.
Note 2: The tab1 command produces one-way frequency tables for a series of variables.
tabulate e, generate(e)
E | Freq. Percent Cum.
------------+-----------------------------------
1 | 14 30.43 30.43
2 | 19 41.30 71.74
3 | 13 28.26 100.00
------------+-----------------------------------
Total | 46 100.00
tab1 e1 e2 e3
-> tabulation of e1
e== |
1.0000 | Freq. Percent Cum.
------------+-----------------------------------
0 | 32 69.57 69.57
1 | 14 30.43 100.00
------------+-----------------------------------
Total | 46 100.00
-> tabulation of e2
e== |
2.0000 | Freq. Percent Cum.
------------+-----------------------------------
0 | 27 58.70 58.70
1 | 19 41.30 100.00
------------+-----------------------------------
Total | 46 100.00
-> tabulation of e3
e== |
3.0000 | Freq. Percent Cum.
------------+-----------------------------------
0 | 33 71.74 71.74
1 | 13 28.26 100.00
------------+-----------------------------------
Total | 46 100.00
Table 5.3, page 126.
regress s x e1 e2 m
Source | SS df MS Number of obs = 46
---------+------------------------------ F( 4, 41) = 226.84
Model | 957816858 4 239454214 Prob > F = 0.0000
Residual | 43280719.5 41 1055627.30 R-squared = 0.9568
---------+------------------------------ Adj R-squared = 0.9525
Total | 1.0011e+09 45 22246612.8 Root MSE = 1027.4
------------------------------------------------------------------------------
s | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
x | 546.184 30.51919 17.896 0.000 484.5493 607.8188
e1 | -2996.21 411.7527 -7.277 0.000 -3827.762 -2164.659
e2 | 147.8249 387.6593 0.381 0.705 -635.0689 930.7188
m | 6883.531 313.919 21.928 0.000 6249.559 7517.503
_cons | 11031.81 383.2171 28.787 0.000 10257.89 11805.73
------------------------------------------------------------------------------
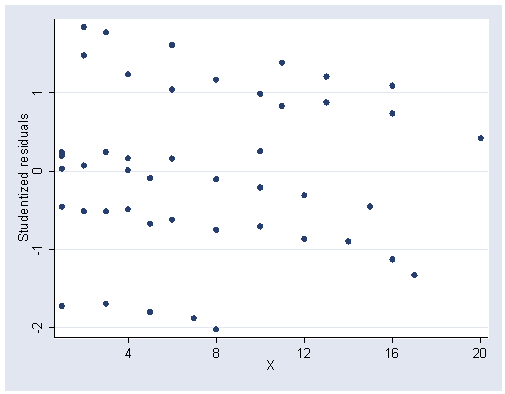
Figure 5.1, page 127. The rvpplot2 can be downloaded within Stata by typing search rvpplot2 (see How can I use the search command to search for programs and get additional help? for more information about using search).
rvpplot2 x, rstudent xlabel(4(4)20) ylabel(-2(1)1)
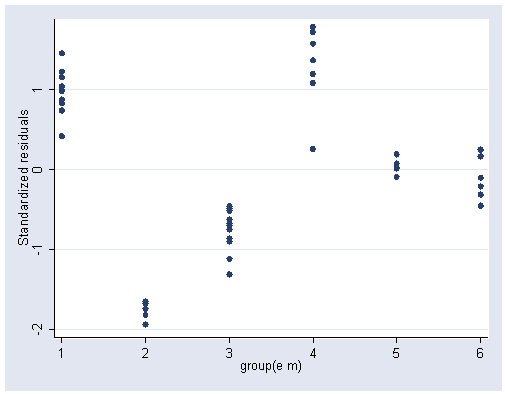
Figure 5.2, page 128.
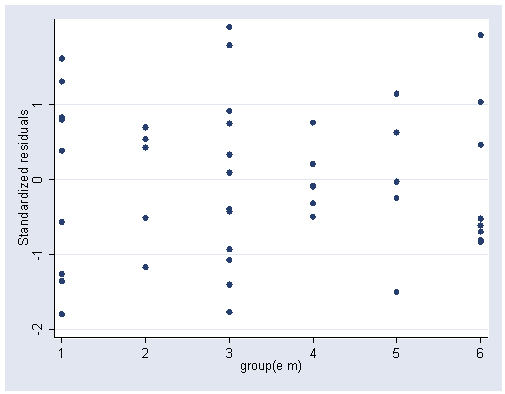
Note 1: The egen command was used with the group function to produce the six categories of education and management.
Note 2: The xlabel(1(1)6) option produces labels on the x-axis from 1 to 6 by ones.
egen c = group(e m) predict sr, rstandard graph twoway scatter sr c, ylabel(-2(1)1) xlabel(1(1)6)
Table 5.4, page 129.
generate e1m = e1*m
generate e2m = e2*m
regress s x e1 e2 m e1m e2m
Source | SS df MS Number of obs = 46
---------+------------------------------ F( 6, 39) = 5516.60
Model | 999919409 6 166653235 Prob > F = 0.0000
Residual | 1178167.86 39 30209.4324 R-squared = 0.9988
---------+------------------------------ Adj R-squared = 0.9986
Total | 1.0011e+09 45 22246612.8 Root MSE = 173.81
------------------------------------------------------------------------------
s | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
x | 496.987 5.566415 89.283 0.000 485.7279 508.2461
e1 | -1730.748 105.3339 -16.431 0.000 -1943.806 -1517.69
e2 | -349.0777 97.5679 -3.578 0.001 -546.4274 -151.728
m | 7047.412 102.5892 68.695 0.000 6839.906 7254.918
e1m | -3066.035 149.3304 -20.532 0.000 -3368.084 -2763.986
e2m | 1836.488 131.1674 14.001 0.000 1571.177 2101.799
_cons | 11203.43 79.06545 141.698 0.000 11043.51 11363.36
------------------------------------------------------------------------------
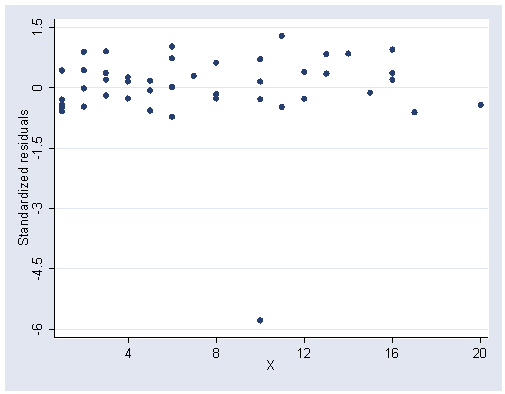
Figure 5.3, page 129.
rvpplot2 x, rstandard xlabel(4(4)20) ylabel(-6(1.5)1.5)
Table 5.5, page 129.
drop if id==33
(1 observation deleted)
regress s x e1 e2 m e1m e2m
Source | SS df MS Number of obs = 45
---------+------------------------------ F( 6, 38) =35427.96
Model | 957607113 6 159601186 Prob > F = 0.0000
Residual | 171188.12 38 4504.95052 R-squared = 0.9998
---------+------------------------------ Adj R-squared = 0.9998
Total | 957778301 44 21767688.7 Root MSE = 67.119
------------------------------------------------------------------------------
s | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
x | 498.4178 2.151688 231.640 0.000 494.0619 502.7736
e1 | -1741.336 40.6825 -42.803 0.000 -1823.693 -1658.979
e2 | -357.0423 37.68114 -9.475 0.000 -433.3237 -280.7608
m | 7040.58 39.61907 177.707 0.000 6960.376 7120.785
e1m | -3051.763 57.6742 -52.914 0.000 -3168.519 -2935.008
e2m | 1997.531 51.78498 38.574 0.000 1892.697 2102.364
_cons | 11199.71 30.53338 366.802 0.000 11137.9 11261.53
------------------------------------------------------------------------------
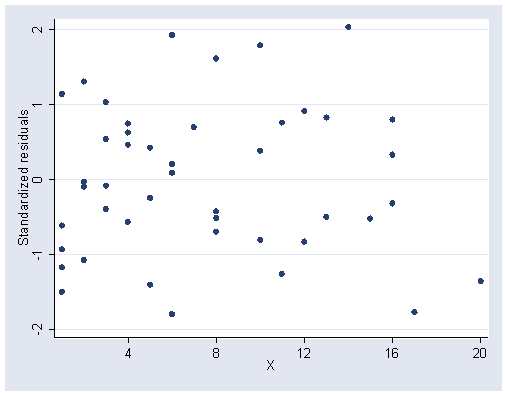
Figure 5.4, page 130.
rvpplot2 x, rstandard xlabel(4(4)20) ylabel(-2(1)2)
Figure 5.5, page 130.
drop sr predict sr, rstandard graph twoway scatter sr c, ylabel(-2(1)1) xlabel(1(1)6)
Table 5.6, page 131.
Note: There are small differences between table 5.6 in the book and the one generated by Stata due to rounding.
adjust x=0, by(m e) se ci format(%5.0f)
-------------------------------------------------------------------------------
Dependent variable: s Command: regress
Variables left as is: e1, e2, e1m, e2m
Covariate set to value: x = 0
-------------------------------------------------------------------------------
----------+--------------------------------------------
| E
M | 1 2 3
----------+--------------------------------------------
0 | 9458 10843 11200
| (31) (26) (31)
| [9396,9521] [10790,10896] [11138,11262]
|
1 | 13447 19881 18240
| (32) (33) (29)
| [13383,13511] [19814,19947] [18183,18298]
----------+--------------------------------------------
Use the data file p134 and create interaction variable.
use https://stats.idre.ucla.edu/stat/stata/examples/chp/p134, clear generate rbyt = race*test
Table 5.8, page 135.
regress jperf test
Source | SS df MS Number of obs = 20
---------+------------------------------ F( 1, 18) = 19.25
Model | 48.7229625 1 48.7229625 Prob > F = 0.0004
Residual | 45.5682959 18 2.531572 R-squared = 0.5167
---------+------------------------------ Adj R-squared = 0.4899
Total | 94.2912585 19 4.96269781 Root MSE = 1.5911
------------------------------------------------------------------------------
jperf | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
test | 2.360535 .5380699 4.387 0.000 1.230092 3.490978
_cons | 1.034973 .8680312 1.192 0.249 -.7886928 2.858639
------------------------------------------------------------------------------
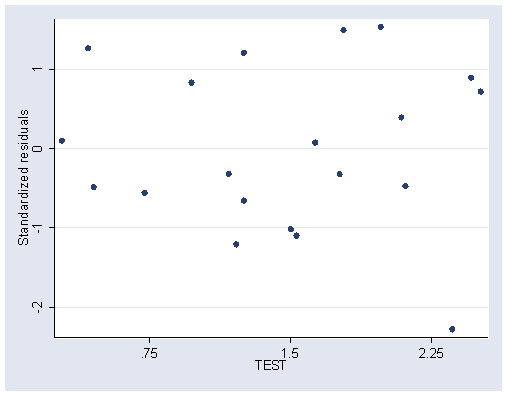
Figure 5.7, page 135.
rvpplot2 test, rstandard ylabel(-2(1)1) xlabel(.75 1.5 2.25)
Figure 5.9, page 137.
predict sr, rstandard graph twoway scatter sr race, ylabel(-2(1)1) xlabel(0 1)
Table 5.9, page 135.
regress jperf test race rbyt
Source | SS df MS Number of obs = 20
---------+------------------------------ F( 3, 16) = 10.55
Model | 62.6357847 3 20.8785949 Prob > F = 0.0005
Residual | 31.6554738 16 1.97846711 R-squared = 0.6643
---------+------------------------------ Adj R-squared = 0.6013
Total | 94.2912585 19 4.96269781 Root MSE = 1.4066
------------------------------------------------------------------------------
jperf | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
test | 1.313402 .6703711 1.959 0.068 -.1077208 2.734525
race | -1.913167 1.540325 -1.242 0.232 -5.178509 1.352176
rbyt | 1.997546 .954443 2.093 0.053 -.0257831 4.020875
_cons | 2.010282 1.050112 1.914 0.074 -.2158562 4.236421
------------------------------------------------------------------------------
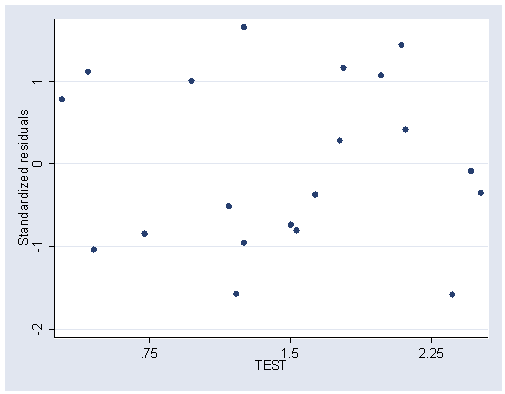
Figure 5.8, page 135.
rvpplot2 test, rstandard ylabel(-2(1)1) xlabel(.75 1.5 2.25)
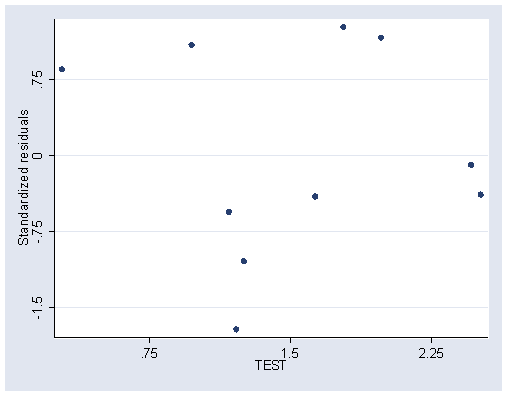
Part of Table 5.10, page 136.
regress jperf test if race==1
Source | SS df MS Number of obs = 10
---------+------------------------------ F( 1, 8) = 28.14
Model | 46.9895716 1 46.9895716 Prob > F = 0.0007
Residual | 13.3568411 8 1.66960513 R-squared = 0.7787
---------+------------------------------ Adj R-squared = 0.7510
Total | 60.3464126 9 6.70515696 Root MSE = 1.2921
------------------------------------------------------------------------------
jperf | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
test | 3.310948 .6241062 5.305 0.001 1.871757 4.75014
_cons | .0971152 1.035193 0.094 0.928 -2.290043 2.484274
------------------------------------------------------------------------------
------------------------------------------------------------------------------
Figure 5.10, page 137.
rvpplot2 test, rstandard ylabel(-1.5(.75).75) xlabel(.75 1.5 2.25)
Remainder of Table 5.10, page 136.
regress jperf test if race==0
Source | SS df MS Number of obs = 10
---------+------------------------------ F( 1, 8) = 3.32
Model | 7.5944073 1 7.5944073 Prob > F = 0.1059
Residual | 18.2986327 8 2.28732909 R-squared = 0.2933
---------+------------------------------ Adj R-squared = 0.2050
Total | 25.89304 9 2.87700445 Root MSE = 1.5124
------------------------------------------------------------------------------
jperf | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
test | 1.313402 .7208006 1.822 0.106 -.3487669 2.975572
_cons | 2.010282 1.129108 1.780 0.113 -.5934463 4.614011
------------------------------------------------------------------------------
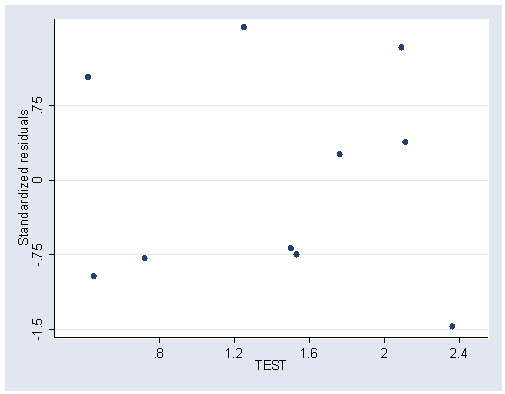
Figure 5.11, page 137.
rvpplot2 test, rstandard ylabel(-1.5(.75).75) xlabel(.8(.4)2.4)