use https://stats.idre.ucla.edu/stat/stata/examples/chp/p157, clear
Table 6.2, page 157.
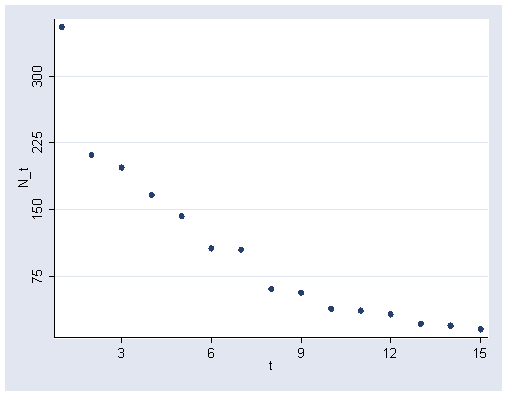
list
t n_t
1. 1 355
2. 2 211
3. 3 197
4. 4 166
5. 5 142
6. 6 106
7. 7 104
8. 8 60
9. 9 56
10. 10 38
11. 11 36
12. 12 32
13. 13 21
14. 14 19
15. 15 15
Figure 6.5, page 159.
graph twoway scatter n_t t, ylabel(75(75)300) xlabel(3(3)15)
Table 6.3, page 159.
regress n_t t
Source | SS df MS Number of obs = 15
---------+------------------------------ F( 1, 13) = 60.62
Model | 106080.357 1 106080.357 Prob > F = 0.0000
Residual | 22749.3762 13 1749.95201 R-squared = 0.8234
---------+------------------------------ Adj R-squared = 0.8098
Total | 128829.733 14 9202.12381 Root MSE = 41.832
------------------------------------------------------------------------------
n_t | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
t | -19.46429 2.499966 -7.786 0.000 -24.86513 -14.06344
_cons | 259.581 22.72999 11.420 0.000 210.4758 308.6861
------------------------------------------------------------------------------
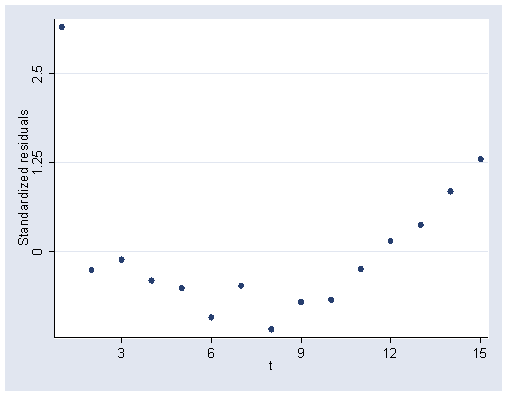
Figure 6.6, page 159. The rvpplot2 command can be downloaded within Stata by typing search rvpplot2 (see How can I use the search command to search for programs and get additional help? for more information about using search).
rvpplot2 t, rstandard ylabel(0 1.25 2.5) xlabel(3(3)15)
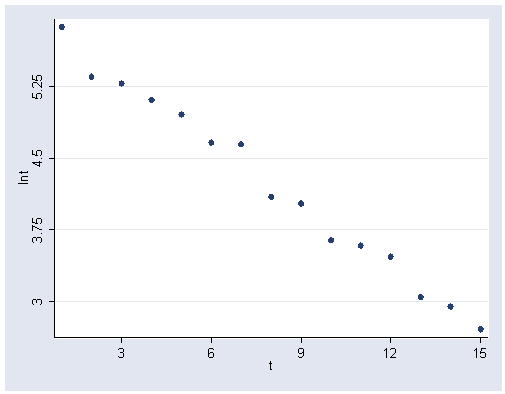
Figure 6.7, page 160.
generate lnt = log(n_t) graph twoway scatter lnt t, ylabel(3(.75)5.25) xlabel(3(3)15)
Table 6.4, page 160.
regress lnt t
Source | SS df MS Number of obs = 15
---------+------------------------------ F( 1, 13) = 1103.70
Model | 13.3586861 1 13.3586861 Prob > F = 0.0000
Residual | .157345913 13 .012103532 R-squared = 0.9884
---------+------------------------------ Adj R-squared = 0.9875
Total | 13.516032 14 .965430858 Root MSE = .11002
------------------------------------------------------------------------------
lnt | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
t | -.2184253 .0065747 -33.222 0.000 -.2326291 -.2042214
_cons | 5.97316 .0597781 99.922 0.000 5.844018 6.102303
------------------------------------------------------------------------------
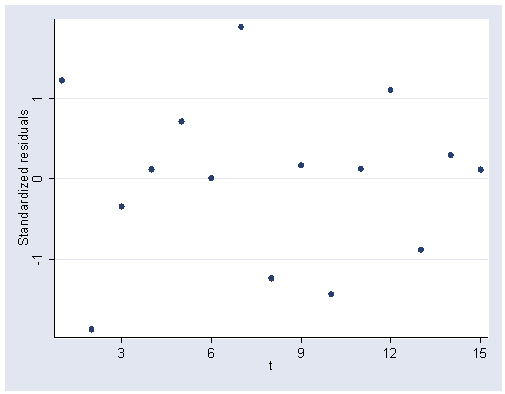
Figure 6.8, page 161.
rvpplot2 t, rstandard ylabel(-1 0 1) xlabel(3(3)15)
Input Airline Injury Data, table 6.6, page 164
Note: The input command can be used to quickly enter small datasets.
clear input y n 11 .095 7 .192 7 .075 19 .2078 9 .1382 4 .054 3 .1292 1 .0503 3 .0629 end save airline
NOTE: Using the save command without a path specification saves the data file in the default Stata directory, which can be seen in the lower left corner of the Stata window.
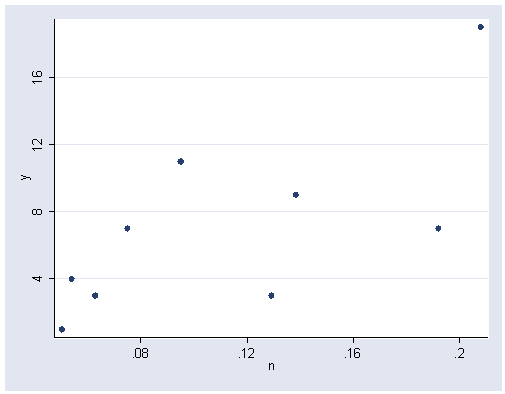
Figure 6.10, page 164
graph twoway scatter y n, ylabel(4(4)16) xlabel(.08(.04).2)
Table 6.7, page 165.
regress y n
Source | SS df MS Number of obs = 9
---------+------------------------------ F( 1, 7) = 6.65
Model | 117.358709 1 117.358709 Prob > F = 0.0365
Residual | 123.53018 7 17.6471686 R-squared = 0.4872
---------+------------------------------ Adj R-squared = 0.4139
Total | 240.888889 8 30.1111111 Root MSE = 4.2009
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
n | 64.97548 25.19587 2.579 0.037 5.396715 124.5542
_cons | -.1401521 3.141233 -0.045 0.966 -7.567989 7.287684
------------------------------------------------------------------------------
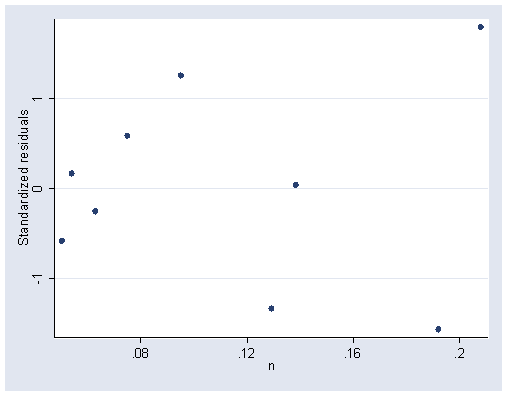
Figure 6.11, page 165.
rvpplot2 n, rstandard ylabel(-1 0 1) xlabel(.08(.04).2)
Table 6.8, page 165.
generate sqrty = sqrt(y)
(6 missing values generated)
regress sqrty n
Source | SS df MS Number of obs = 9
---------+------------------------------ F( 1, 7) = 6.53
Model | 3.90772909 1 3.90772909 Prob > F = 0.0378
Residual | 4.18610486 7 .59801498 R-squared = 0.4828
---------+------------------------------ Adj R-squared = 0.4089
Total | 8.09383395 8 1.01172924 Root MSE = .77331
------------------------------------------------------------------------------
sqrty | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
n | 11.85643 4.638183 2.556 0.038 .8888735 22.82399
_cons | 1.16917 .5782541 2.022 0.083 -.198184 2.536523
------------------------------------------------------------------------------
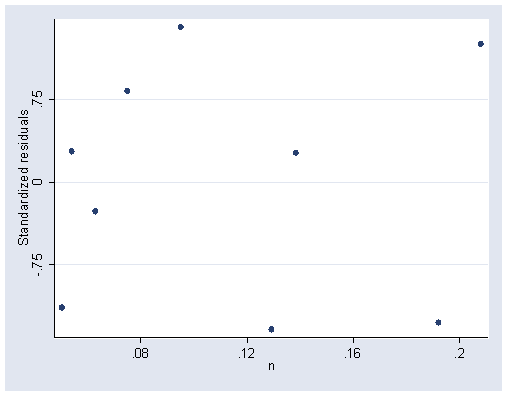
Figure 6.12, page 166.
rvpplot2 n, rstandard ylabel(-.75 0 .75) xlabel(.08(.04).2)
Table 6.9, page 167.
use https://stats.idre.ucla.edu/stat/stata/examples/chp/p167, clear
list
list
x y
1. 294 30
2. 247 32
3. 267 37
4. 358 44
5. 423 47
..
[remainder of output omitted]
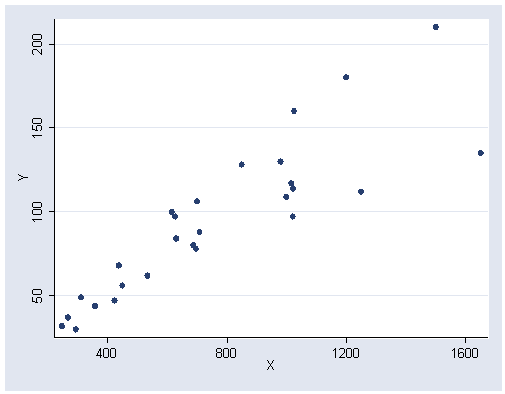
Figure 6.13, page 167.
graph twoway scatter y x, ylabel(50(50)200) xlabel(400(400)1600)
Table 6.10, page 167.
regress y x
Source | SS df MS Number of obs = 27
---------+------------------------------ F( 1, 25) = 86.54
Model | 40862.6027 1 40862.6027 Prob > F = 0.0000
Residual | 11804.064 25 472.16256 R-squared = 0.7759
---------+------------------------------ Adj R-squared = 0.7669
Total | 52666.6667 26 2025.64103 Root MSE = 21.729
------------------------------------------------------------------------------
y | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
x | .1053611 .0113256 9.303 0.000 .0820355 .1286867
_cons | 14.44806 9.562012 1.511 0.143 -5.245273 34.14139
------------------------------------------------------------------------------
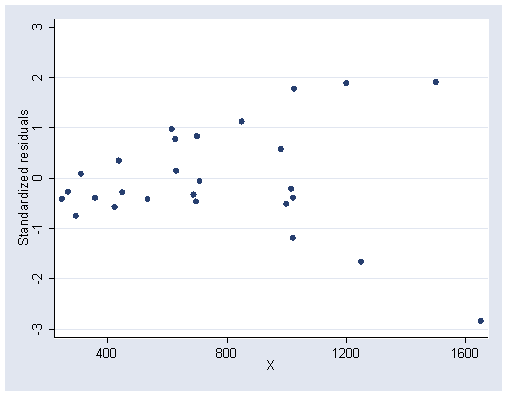
Figure 6.14, page 168.
rvpplot2 x, rstandard ylabel(-3(1)3) xlabel(400(400)1600)
Transformations of y and x, page 168.
generate ty = y/x generate tx = 1/x
Regression used to obtain coefficients of Table 6.11, page 169.
regress ty tx
Source | SS df MS Number of obs = 27
---------+------------------------------ F( 1, 25) = 0.69
Model | .000355828 1 .000355828 Prob > F = 0.4131
Residual | .012842316 25 .000513693 R-squared = 0.0270
---------+------------------------------ Adj R-squared = -0.0120
Total | .013198144 26 .000507621 Root MSE = .02266
------------------------------------------------------------------------------
ty | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
tx | 3.803296 4.569745 0.832 0.413 -5.60827 13.21486
_cons | .1209903 .0089986 13.445 0.000 .1024573 .1395233
------------------------------------------------------------------------------
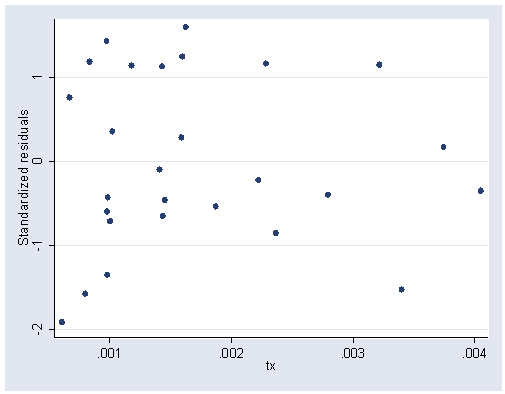
Figure 6.15, page 169. The rvfpplot2 command can be downloaded within Stata by typing search rvfplot2 (see How can I use the search command to search for programs and get additional help? for more information about using search).
rvpplot2 tx, rstandard ylabel(-2(1)1) xlabel(.001(.001).004)
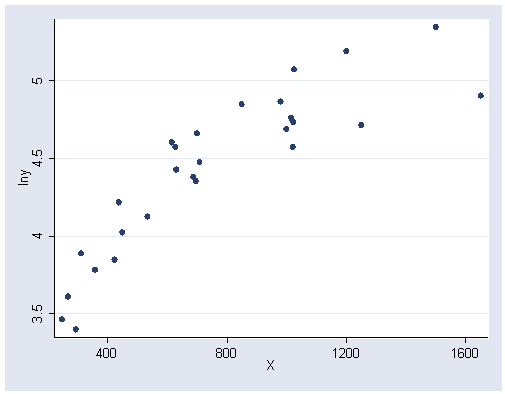
Figure 6.16, page 171.
generate lny = log(y) graph twoway scatter lny x, ylabel(3.5(.5)5) xlabel(400(400)1600)
Table 6.12, page 171
regress lny x
Source | SS df MS Number of obs = 27
---------+------------------------------ F( 1, 25) = 83.77
Model | 5.33672231 1 5.33672231 Prob > F = 0.0000
Residual | 1.59258745 25 .063703498 R-squared = 0.7702
---------+------------------------------ Adj R-squared = 0.7610
Total | 6.92930976 26 .266511914 Root MSE = .2524
------------------------------------------------------------------------------
lny | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
x | .0012041 .0001316 9.153 0.000 .0009331 .001475
_cons | 3.515023 .111067 31.648 0.000 3.286276 3.74377
------------------------------------------------------------------------------
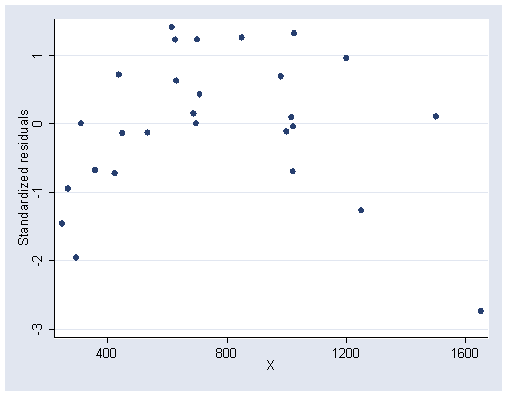
Figure 6.17, page 171.
rvpplot2 x, rstandard ylabel(-3(1)1) xlabel(400(400)1600)
Table 6.13, page 172.
generate x2 = x^2
regress lny x x2
Source | SS df MS Number of obs = 27
---------+------------------------------ F( 2, 24) = 92.98
Model | 6.137239 2 3.0686195 Prob > F = 0.0000
Residual | .792070761 24 .033002948 R-squared = 0.8857
---------+------------------------------ Adj R-squared = 0.8762
Total | 6.92930976 26 .266511914 Root MSE = .18167
------------------------------------------------------------------------------
lny | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
x | .0031127 .0003989 7.803 0.000 .0022893 .003936
x2 | -1.10e-06 2.24e-07 -4.925 0.000 -1.56e-06 -6.40e-07
_cons | 2.8516 .1566401 18.205 0.000 2.528311 3.17489
------------------------------------------------------------------------------
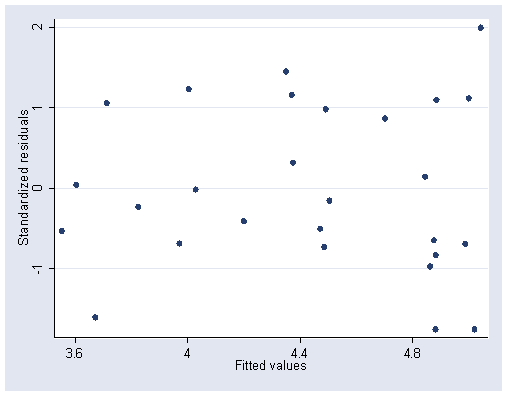
Figure 6.18, page 172.
rvfplot2, rstandard ylabel(-1(1)2) xlabel(3.6(.4)4.8)
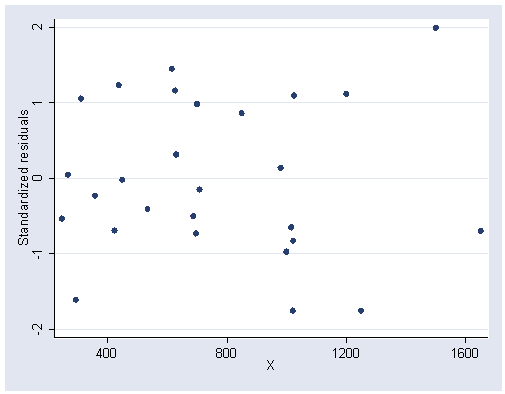
Figure 6.19, page 173.
rvpplot2 x, rstandard ylabel(-2(1)2) xlabel(400(400)1600)
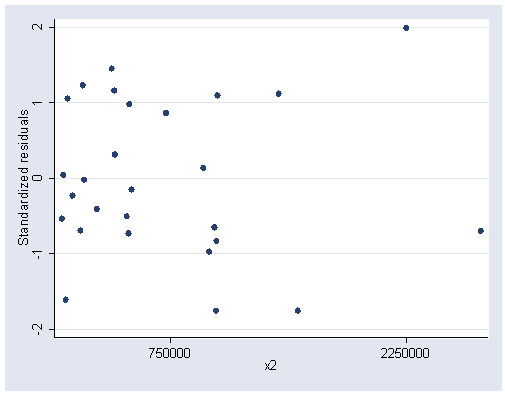
Figure 6.20, page 173.
rvpplot2 x2, rstandard ylabel(-2(1)2) xlabel(750000 2250000)
Table 6.14, page 166.
use https://stats.idre.ucla.edu/stat/stata/examples/chp/p176, clear
list
name brainwei bodyweig
1. Mountain beaver 8.1 1.35
2. Cow 423 465
3. Graywolf 119.5 36.33
4. Goat 115 27.66
5. Guineapig 5.5 1.04
6. Diplodocus 50 11700
..
[remainder of output omitted]
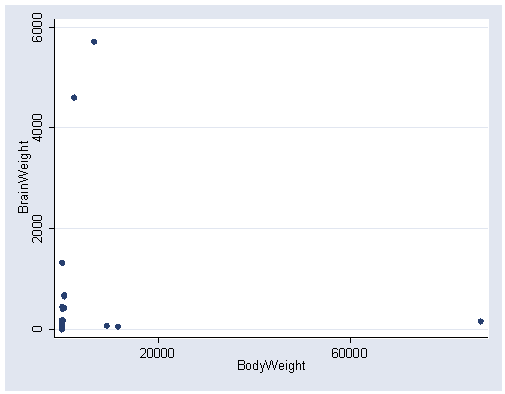
Figure 6.21, page 175.
graph twoway scatter brainwei bodyweig, xlabel(20000 60000)
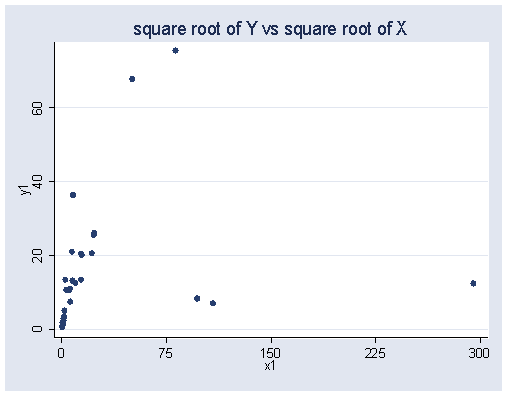
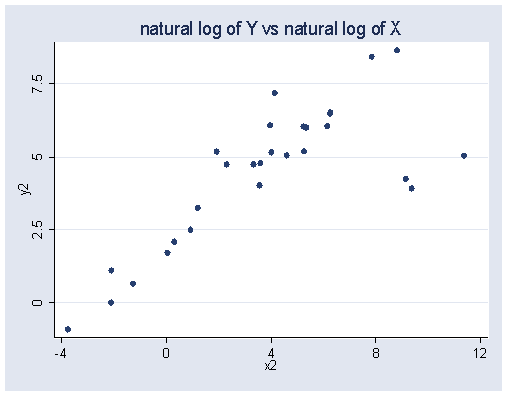
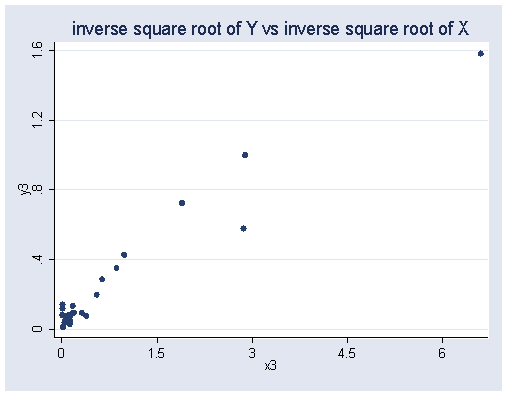
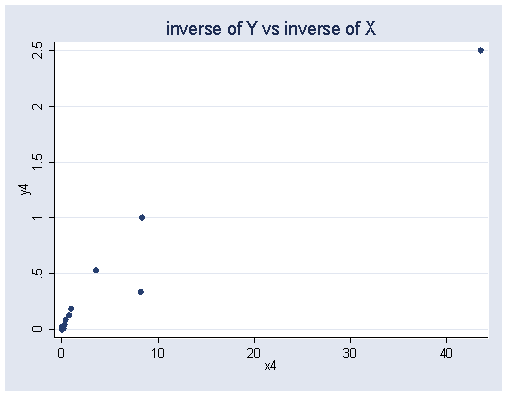
Power transformations, page 175.
generate y1 = brainwei^.5 generate x1 = bodyweig^.5 generate y2 = log(brainwei) generate x2 = log(bodyweig) generate y3 = brainwei^-.5 generate x3 = bodyweig^-.5 generate y4 = brainwei^-1 generate x4 = bodyweig^-1
Figure 6.22, page 175.
graph twoway scatter y1 x1, ylabel(0(20)60) xlabel(0(75)300) ///
title("square root of Y vs square root of X")
graph twoway scatter y2 x2, ylabel(0(2.5)7.5) xlabel(-4(4)12) ///
title("natural log of Y vs natural log of X")
graph twoway scatter y3 x3, ylabel(0(.4)1.6) xlabel(0(1.5)6) ///
title("inverse square root of Y vs inverse square root of X")
graph twoway scatter y4 x4, ylabel(0(.5)2.5) xlabel(0(10)40) ///
title("inverse of Y vs inverse of X")