Note: Variables in book are labeled incorrectly. The first variable is achv followed by fam, peer and school.
Tables 9.1 and 9.2, pages 228 and 229.
use https://stats.idre.ucla.edu/stat/stata/examples/chp/p228, clear
list
achv fam peer school
1. -.43148 .60814 .03509 .16607
2. .79969 .79369 .47924 .53356
3. -.92467 -.8263 -.61951 -.78635
4. -2.19081 -1.2531 -1.21675 -1.04076
5. -2.84818 .17399 -.18517 .14229
6. -.66233 .20246 .12764 .27311
7. 2.63674 .24184 -.09022 .04967
8. 2.35847 .59421 .2175 .51876
9. -.91305 -.61561 -.48971 -.63219
10. .59445 .99391 .62228 .93368
..
[remainder of output omitted]
Table 9.3, page 229.
regress achv fam peer school
Source | SS df MS Number of obs = 70
-------------+------------------------------ F( 3, 66) = 5.72
Model | 73.5062325 3 24.5020775 Prob > F = 0.0015
Residual | 282.873224 66 4.28595794 R-squared = 0.2063
-------------+------------------------------ Adj R-squared = 0.1702
Total | 356.379456 69 5.16491966 Root MSE = 2.0703
------------------------------------------------------------------------------
achv | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
fam | 1.10126 1.410562 0.78 0.438 -1.715017 3.917537
peer | 2.322057 1.481287 1.57 0.122 -.6354284 5.279542
school | -2.280996 2.220448 -1.03 0.308 -6.714263 2.152272
_cons | -.0699591 .2506421 -0.28 0.781 -.5703821 .4304639
------------------------------------------------------------------------------
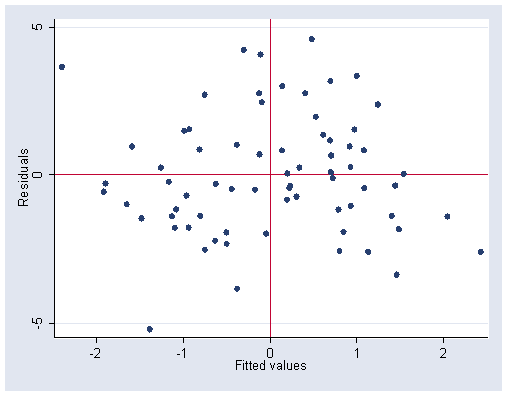
Figure 9.1, page 229.
Note: The rvfplot command uses the raw residuals and not standardized residuals.
rvfplot, yline(0) xline(0)
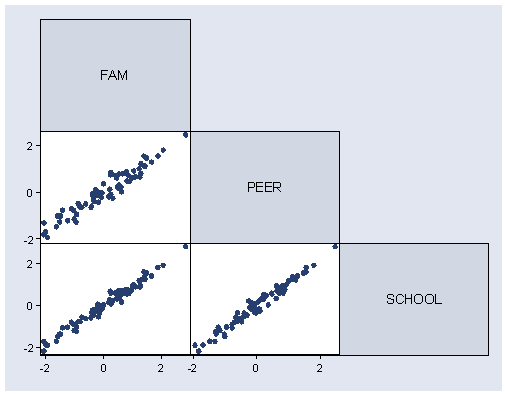
Figure 9,2, page 231.
corr fam peer school
(obs=70)
| fam peer school
---------+---------------------------
fam | 1.0000
peer | 0.9601 1.0000
school | 0.9857 0.9822 1.0000
graph matrix fam peer school, half
Table 9.12, part 1, page 242.
Note: The collin command can be downloaded from UCLA ATS from within Stata (see How can I use the search command to search for programs and get additional help? for more information about using search).
collin fam peer school
Collinearity Diagnostics
SQRT Cond
Variable VIF VIF Tolerance Eigenval Index
-------------------------------------------------------------
fam 37.58 6.13 0.0266 2.9520 1.0000
peer 30.21 5.50 0.0331 0.0400 8.5856
school 83.16 9.12 0.0120 0.0080 19.2584
-------------------------------------------------------------
Mean VIF 50.32 Condition Number 19.2584
Table 9.5, page 233.
use https://stats.idre.ucla.edu/stat/stata/examples/chp/p233, clear
generate index = _n
list
year import doprod stock consum index
1. 49 15.9 149.3 4.2 108.1 1
2. 50 16.4 161.2 4.1 114.8 2
3. 51 19 171.5 3.1 123.2 3
4. 52 19.1 175.5 3.1 126.9 4
5. 53 18.8 180.8 1.1 132.1 5
6. 54 20.4 190.7 2.2 137.7 6
7. 55 22.7 202.1 2.1 146 7
8. 56 26.5 212.4 5.6 154.1 8
9. 57 28.1 226.1 5 162.3 9
10. 58 27.6 231.9 5.1 164.3 10
11. 59 26.3 239 .7 167.6 11
12. 60 31.1 258 5.6 176.8 12
13. 61 33.3 269.8 3.9 186.6 13
14. 62 37 288.4 3.1 199.7 14
15. 63 43.3 304.5 4.6 213.9 15
16. 64 49 323.4 7 223.8 16
17. 65 50.3 336.8 1.2 232 17
18. 66 56.6 353.9 4.5 242.9 18
Table 9.6, page 234.
regress import doprod stock consum Source | SS df MS Number of obs = 18 ---------+------------------------------ F( 3, 14) = 168.45 Model | 2576.92062 3 858.97354 Prob > F = 0.0000 Residual | 71.3903825 14 5.09931304 R-squared = 0.9730 ---------+------------------------------ Adj R-squared = 0.9673 Total | 2648.311 17 155.783 Root MSE = 2.2582 ------------------------------------------------------------------------------ import | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- doprod | .0322051 .1868844 0.172 0.866 -.3686221 .4330324 stock | .4141991 .3222598 1.285 0.220 -.2769794 1.105378 consum | .242746 .2853608 0.851 0.409 -.3692921 .8547841 _cons | -19.7251 4.125254 -4.782 0.000 -28.57289 -10.87731 ------------------------------------------------------------------------------
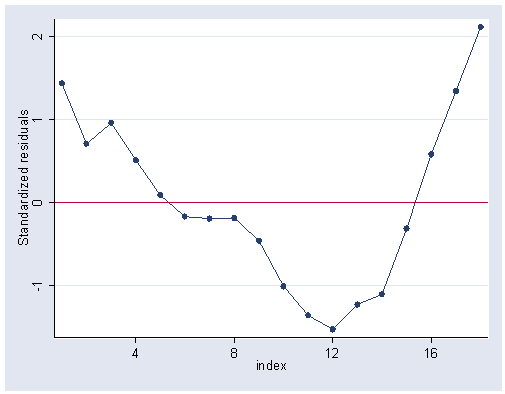
Figure 9.3, page 234.
predict r, rstandard graph twoway scatter r index, connect(l) yline(0) ylabel(-1(1)2) xlabel(4(4)16)
Table 9.7, page 235.
drop if year>=60 regress import doprod stock consum Source | SS df MS Number of obs = 11 ---------+------------------------------ F( 3, 7) = 285.61 Model | 204.776154 3 68.2587179 Prob > F = 0.0000 Residual | 1.67295319 7 .238993312 R-squared = 0.9919 ---------+------------------------------ Adj R-squared = 0.9884 Total | 206.449107 10 20.6449107 Root MSE = .48887 ------------------------------------------------------------------------------ import | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- doprod | -.0513959 .0702801 -0.731 0.488 -.217582 .1147901 stock | .5869492 .0946185 6.203 0.000 .3632119 .8106865 consum | .2868483 .1022083 2.807 0.026 .0451642 .5285325 _cons | -10.12798 1.212161 -8.355 0.000 -12.99429 -7.26168 ------------------------------------------------------------------------------
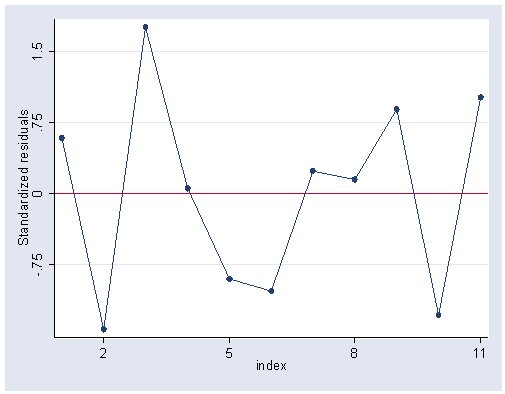
Figure 9.4, page 234.
predict r1, rstandard graph twoway scatter r1 index, connect(l) yline(0) ylabel(-.75(.75)1.5) xlabel(2(3)11)
Table 9.8, page 237.
Note: Output has been edited to include just the constant and the coefficients.
regress import doprod doprod | .1461991 _cons | -6.558102 regress import stock stock | .690809 _cons | 19.61124 regress import consum consum | .2140041 _cons | -8.013247 regress import doprod stock doprod | .1453144 stock | .6224793 _cons | -8.440141 regress import doprod consum doprod | -.1087521 consum | .3716812 _cons | -8.884304 regress import stock consum stock | .5960524 consum | .2123046 _cons | -9.742739 regress import doprod stock consum doprod | -.0513959 stock | .5869492 consum | .2868483 _cons | -10.12798
Table 9.12, part 2, page 242.
Note: These results are for the entire sample from 1949-1966.
collin doprod stock consum
Collinearity Diagnostics
SQRT Cond
Variable VIF VIF Tolerance Eigenval Index
-------------------------------------------------------------
doprod 469.74 21.67 0.0021 2.0839 1.0000
stock 1.05 1.02 0.9525 0.9150 1.5091
consum 469.37 21.66 0.0021 0.0011 44.2258
-------------------------------------------------------------
Mean VIF 313.39 Condition Number 44.2258
use https://stats.idre.ucla.edu/stat/stata/examples/chp/p238
Table 9.9, page 238.
generate index = _n
list index s_t a_t p_t e_t
index s_t a_t p_t e_t
1. 1 20.11371 1.98786 1 .3
2. 2 15.10439 1.94418 0 .3
3. 3 18.68375 2.19954 .8 .35
4. 4 16.05173 2.00107 0 .35
5. 5 21.30101 1.69292 1.3 .3
6. 6 17.85004 1.74334 .3 .32
7. 7 18.87558 2.06907 1 .31
8. 8 21.26599 1.01709 1 .41
9. 9 20.48473 2.01906 .9 .45
10. 10 20.54032 1.06139 1 .45
..
[remainder of output omitted]
list index a_t1 p_t1
index a_t1 p_t1
1. 1 2.01722 0
2. 2 1.98786 1
3. 3 1.94418 0
4. 4 2.19954 .8
5. 5 2.00107 0
6. 6 1.69292 1.3
7. 7 1.74334 .3
8. 8 2.06907 1
9. 9 1.01709 1
10. 10 2.01906 .9
..
[remainder of output omitted]
Table 9.11, page 239.
corr a_t p_t e_t a_t1
(obs=22)
| a_t p_t e_t a_t1 p_t1
---------+---------------------------------------------
a_t | 1.0000
p_t | -0.3570 1.0000
e_t | -0.1285 0.0626 1.0000
a_t1 | -0.1397 -0.3165 -0.1664 1.0000
p_t1 | -0.4960 -0.2964 0.2081 -0.3578 1.0000
Table 9.10, page 239.
regress s_t a_t p_t e_t a_t1 p_t1
Source | SS df MS Number of obs = 22
---------+------------------------------ F( 5, 16) = 35.30
Model | 307.571804 5 61.5143607 Prob > F = 0.0000
Residual | 27.8786967 16 1.74241854 R-squared = 0.9169
---------+------------------------------ Adj R-squared = 0.8909
Total | 335.4505 21 15.9738333 Root MSE = 1.32
------------------------------------------------------------------------------
s_t | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
a_t | 5.360753 4.027685 1.331 0.202 -3.177559 13.89906
p_t | 8.372322 3.586411 2.334 0.033 .7694711 15.97517
e_t | 22.52103 2.142351 10.512 0.000 17.97945 27.06261
a_t1 | 3.85457 3.577717 1.077 0.297 -3.729852 11.43899
p_t1 | 4.124796 3.895108 1.059 0.305 -4.132463 12.38206
_cons | -14.19368 18.7151 -0.758 0.459 -53.86792 25.48057
------------------------------------------------------------------------------
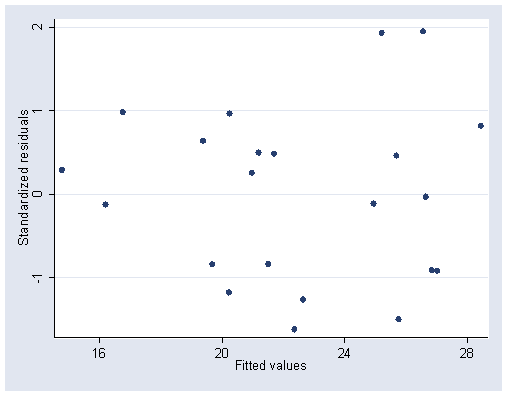
Figure 9.5, page 239.
predict p predict r, rstandard graph twoway scatter r p, ylabel(-1(1)2) xlabel(16(4)28)
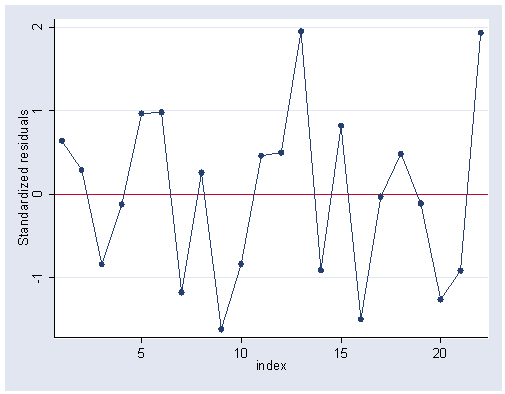
Figure 9.6, page 240.
graph r index, c(l) yline(0) ylabel xlabel
Table 9.12, part 3, page 242.
collin a_t p_t e_t a_t1 p_t1
Collinearity Diagnostics
SQRT Cond
Variable VIF VIF Tolerance Eigenval Index
-------------------------------------------------------------
a_t 36.94 6.08 0.0271 1.7010 1.0000
p_t 33.47 5.79 0.0299 1.2882 1.1491
e_t 1.08 1.04 0.9294 1.1447 1.2190
a_t1 25.92 5.09 0.0386 0.8589 1.4072
p_t1 43.52 6.60 0.0230 0.0073 15.2946
-------------------------------------------------------------
Mean VIF 28.19 Condition Number 15.2946
Table 9.13, page 247.
use https://stats.idre.ucla.edu/stat/stata/examples/chp/p233, clear
drop if year >= 60
generate index = _n
factor doprod stock consum, pc factors(3)
score c1 c2 c3
list c1 c2 c3
c1 c2 c3
1. -2.125887 .638658 .0207224
2. -1.618927 .5555392 .071113
3. -1.115168 -.0729797 .0217302
4. -.8942966 -.08237 -.0108132
5. -.6442078 -1.306685 -.0725826
6. -.1903517 -.6591474 -.0265525
7. .359622 -.7436745 -.042781
8. .9718018 1.354059 -.0628627
9. 1.559316 .9640456 -.0235742
10. 1.766995 1.015217 .0449881
11. 1.931103 -1.662662 .0806126
Formula middle page 250.
Note: Constrained regression is similar to table 9.14, page 250.
constraint define 1 doprod = consum
cnsreg import doprod stock consum, c(1)
Constrained linear regression Number of obs = 11
F( 2, 8) = 314.45
Prob > F = 0.0000
Root MSE = .56934
( 1) doprod - consum = 0.0
------------------------------------------------------------------------------
import | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
doprod | .0863804 .0035597 24.266 0.000 .0781717 .094589
stock | .6116376 .1092145 5.600 0.001 .3597885 .8634867
consum | .0863804 .0035597 24.266 0.000 .0781717 .094589
_cons | -9.006805 1.245017 -7.234 0.000 -11.87782 -6.135791
------------------------------------------------------------------------------
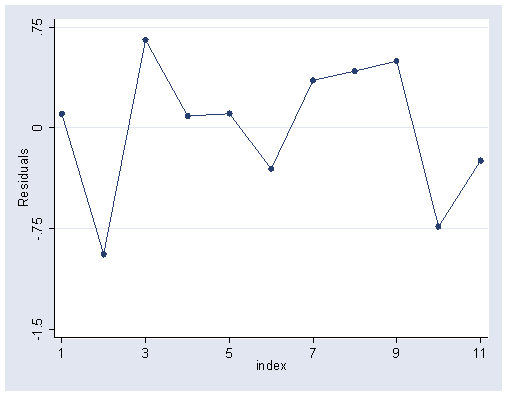
Figure 9.7, page 251.
Note: These residuals are raw residuals not standardized.
predict r, residual graph twoway scatter r index, c(l) ylabel(-1.5(.75).75) xlabel(1(2)11)
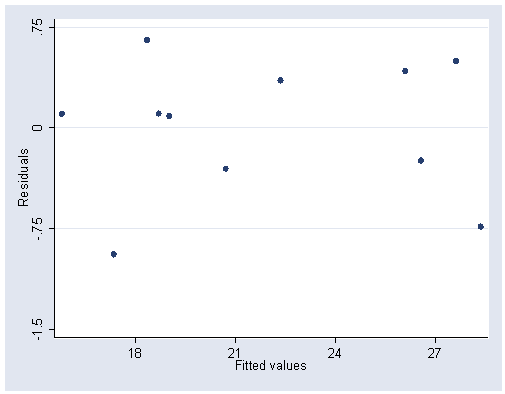
Figure 9.8, page 251.
predict p graph twoway scatter r p, ylabel(-1.5(.75).75) xlabel(18(3)27)
Table 9.15, page 253.
gen new = 2/3*doprod
regress import doprod stock new
Source | SS df MS Number of obs = 11
---------+------------------------------ F( 2, 8) = 228.27
Model | 202.893726 2 101.446863 Prob > F = 0.0000
Residual | 3.55538138 8 .444422672 R-squared = 0.9828
---------+------------------------------ Adj R-squared = 0.9785
Total | 206.449107 10 20.6449107 Root MSE = .66665
------------------------------------------------------------------------------
import | Coef. Std. Err. t P>|t| [95% Conf. Interval]
---------+--------------------------------------------------------------------
doprod | .1453144 .0070296 20.672 0.000 .1291042 .1615247
stock | .6224793 .1278671 4.868 0.001 .3276172 .9173413
new | (dropped)
_cons | -8.440141 1.435179 -5.881 0.000 -11.74967 -5.130612
------------------------------------------------------------------------------
Equations 9.27 and 9.32, pages 253 and 254.
use https://stats.idre.ucla.edu/stat/stata/examples/chp/p238, clear
factor a_t p_t e_t a_t1 p_t1, pc factors(5) /* Stata 8 */
pca a_t p_t e_t a_t1 p_t1 /* Stata 9 */
(obs=22)
(principal components; 5 components retained)
Component Eigenvalue Difference Proportion Cumulative
------------------------------------------------------------------
1 1.70095 0.41275 0.3402 0.3402
2 1.28821 0.14356 0.2576 0.5978
3 1.14465 0.28574 0.2289 0.8268
4 0.85892 0.85164 0.1718 0.9985
5 0.00727 . 0.0015 1.0000
Eigenvectors
Variable | 1 2 3 4 5
----------+------------------------------------------------------
a_t | -0.53245 -0.02379 0.66774 0.07442 0.51432
p_t | 0.23245 0.82494 -0.15779 -0.03711 0.48904
e_t | 0.38909 -0.02208 0.21721 0.89490 -0.00971
a_t1 | -0.39523 -0.25964 -0.69191 0.33802 0.42824
p_t1 | 0.59571 -0.50100 0.05747 -0.27925 0.55932
score c1 c2 c3 c4 c5 /* Stata 8 */
predict c1 c2 c3 c4 c5, score /* Stata 9 */
(based on unrotated principal components)
Scoring Coefficients
Variable | 1 2 3 4 5
----------+------------------------------------------------------
a_t | -0.53245 -0.02379 0.66774 0.07442 0.51432
p_t | 0.23245 0.82494 -0.15779 -0.03711 0.48904
e_t | 0.38909 -0.02208 0.21721 0.89490 -0.00971
a_t1 | -0.39523 -0.25964 -0.69191 0.33802 0.42824
p_t1 | 0.59571 -0.50100 0.05747 -0.27925 0.55932
Table 9.16, pages 256.
regress s_t a_t p_t e_t a_t1 p_t1, beta
Source | SS df MS Number of obs = 22
---------+------------------------------ F( 5, 16) = 35.30
Model | 307.571804 5 61.5143607 Prob > F = 0.0000
Residual | 27.8786967 16 1.74241854 R-squared = 0.9169
---------+------------------------------ Adj R-squared = 0.8909
Total | 335.4505 21 15.9738333 Root MSE = 1.32
------------------------------------------------------------------------------
s_t | Coef. Std. Err. t P>|t| Beta
---------+--------------------------------------------------------------------
a_t | 5.360753 4.027685 1.331 0.202 .5830283
p_t | 8.372322 3.586411 2.334 0.033 .9734163
e_t | 22.52103 2.142351 10.512 0.000 .7858832
a_t1 | 3.85457 3.577717 1.077 0.297 .3952874
p_t1 | 4.124796 3.895108 1.059 0.305 .503494
_cons | -14.19368 18.7151 -0.758 0.459 .
------------------------------------------------------------------------------
Table 9.17, pages 257.
Note 1: The egen command was used to obtain the standard score for s_t.
Note 2: These results are slightly different from those in the book, although the r-squared, adjusted r-squared and standard error of estimate are identical to three decimal places.
egen zs_t = std(s_t) regress zs_t c1 c2 c3 c4 c5, hascons (note: hascons false)
Source | SS df MS Number of obs = 22
-------------+------------------------------ F( 5, 16) = 35.30
Model | 19.2547272 5 3.85094544 Prob > F = 0.0000
Residual | 1.74527279 16 .109079549 R-squared = 0.9169
-------------+------------------------------ Adj R-squared = 0.8909
Total | 21 21 1 Root MSE = .33027
------------------------------------------------------------------------------
zs_t | Coef. Std. Err. t P>|t| [95% Conf. Interval]
-------------+----------------------------------------------------------------
c1 | .3653279 .0552606 6.61 0.000 .2481806 .4824751
c2 | .4169108 .0634993 6.57 0.000 .2822982 .5515234
c3 | .1618494 .0673636 2.40 0.029 .0190449 .3046538
c4 | .7035709 .0777655 9.05 0.000 .5387155 .8684264
c5 | 1.219158 .8451888 1.44 0.168 -.5725626 3.010878
_cons | 1.99e-09 .0704142 0.00 1.000 -.1492715 .1492715
------------------------------------------------------------------------------