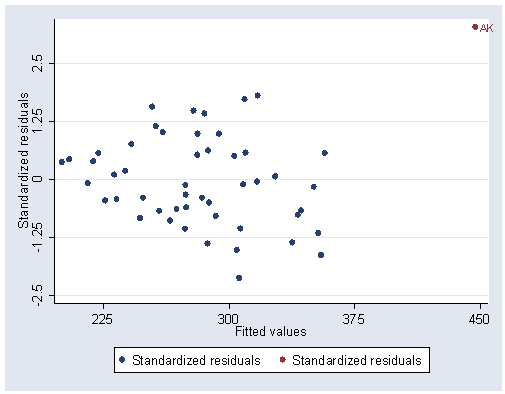
/* Table 7.3, page 189. */use https://stats.idre.ucla.edu/stat/stata/examples/chp/p189, clear liststate y x1 x2 x3 region 1. ME 235 3944 325 508 1 2. NH 231 4578 323 564 1 3. VT 270 4011 328 322 1 4. MA 261 5233 305 846 1 5. RI 300 4780 303 871 1 6. CT 317 5889 307 774 1 7. NY 387 5663 301 856 1 8. NJ 285 5759 310 889 1 9. PA 300 4894 300 715 1 10. OH 221 5012 324 753 2 .. [remainder of output deleted] /* Table 7.4, page 191 */regress y x1 x2 x3Source | SS df MS Number of obs = 50 ---------+------------------------------ F( 3, 46) = 22.19 Model | 109020.418 3 36340.1394 Prob > F = 0.0000 Residual | 75347.5819 46 1637.99091 R-squared = 0.5913 ---------+------------------------------ Adj R-squared = 0.5647 Total | 184368.00 49 3762.61224 Root MSE = 40.472 ------------------------------------------------------------------------------ y | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- x1 | .0723853 .0116024 6.239 0.000 .0490308 .0957398 x2 | 1.552054 .3146716 4.932 0.000 .9186534 2.185456 x3 | -.004269 .0513929 -0.083 0.934 -.1077175 .0991794 _cons | -556.568 123.1953 -4.518 0.000 -804.5472 -308.5889 ------------------------------------------------------------------------------/* Figure 7.3, page 191. */ /* In the book the outlying data point is AL, in our data set that point corresponds to AK. */ predict p predict r, rstandard graph twoway (scatter r p) (scatter r p if state == "AK", mlabel(state)), /// ylabel(-2.5(1.25)2.5) xlabel(225(75)450)
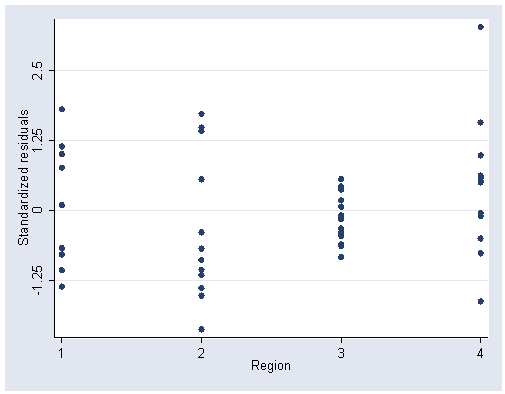
/* Figure 7.4, page 191 */
graph twoway scatter r region, ylabel(-1.25(1.25)2.5) xlabel(1(1)4)
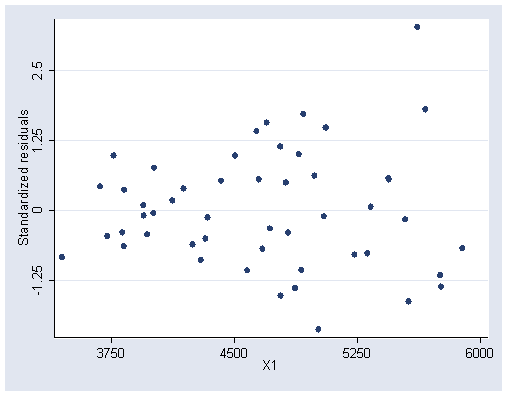
/* Figure 7.5, page 192 */
graph twoway scatter r x1, ylabel(-1.25(1.25)2.5)
xlabel(3750(750)6000)
/* Figure 7.6, page 192 */
graph twoway scatter r x2, ylabel(-1.25(1.25)2.5) xlabel(300(25)375)
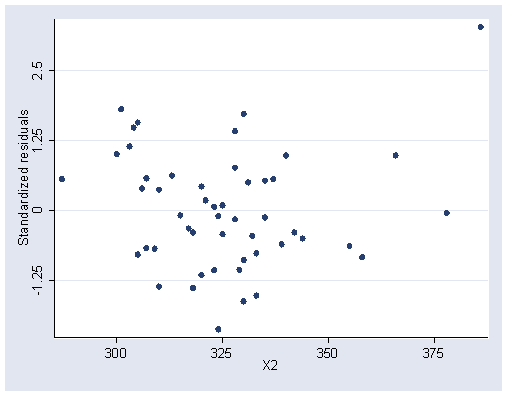
/* Figure 7.7, page 192 */
graph twoway scatter r x3, ylabel(-1.25(1.25)2.5) xlabel(450(150)900)
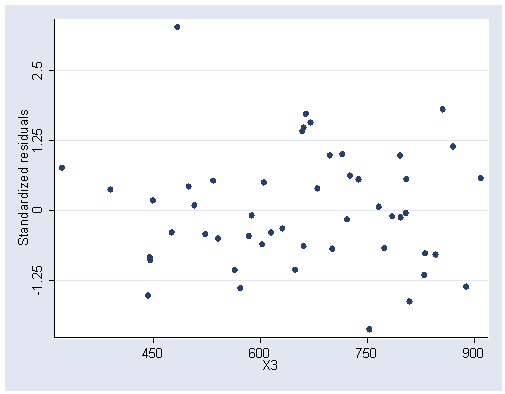
/* Table 7.5, page 193 */ drop if state=="AK" regress y x1 x2 x3Source | SS df MS Number of obs = 49 ---------+------------------------------ F( 3, 45) = 14.80 Model | 56943.7919 3 18981.264 Prob > F = 0.0000 Residual | 57699.7591 45 1282.21687 R-squared = 0.4967 ---------+------------------------------ Adj R-squared = 0.4631 Total | 114643.551 48 2388.40731 Root MSE = 35.808 ------------------------------------------------------------------------------ y | Coef. Std. Err. t P>|t| [95% Conf. Interval] ---------+-------------------------------------------------------------------- x1 | .0482933 .012147 3.976 0.000 .0238281 .0727586 x2 | .8869283 .33114 2.678 0.010 .219978 1.553879 x3 | .0667917 .04934 1.354 0.183 -.0325841 .1661675 _cons | -277.5773 132.4229 -2.096 0.042 -544.2906 -10.86399 ------------------------------------------------------------------------------/* Figure 7.8, page 194 */ predict p2 predict r2, rstandard graph twoway scatter r2 p2, ylabel(-1.25 0 1.25) xlabel(240 280 320)
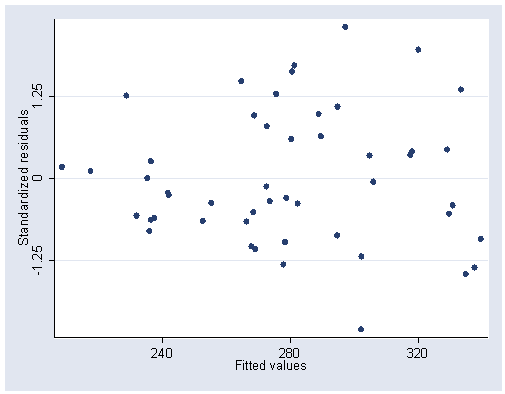
/* Figure 7.9, page 194 */
graph twoway scatter r2 region, ylabel(-2.5(1.25)2.5) xlabel(1(1)4)
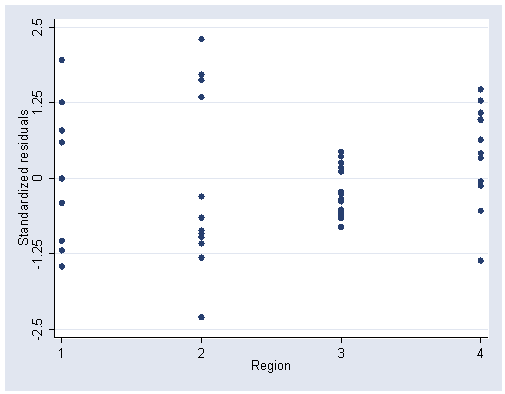
/* Part of Table 7.6, page 195 */ /* Computing the weights from the data */ regress y x1 x2 x3 predict e, resid generate e2 = e^2 bysort region: gen count = _N gen e2_adj = e2/(count-1) egen s2 = sum(e2_adj), by(region) summarize e2Variable | Obs Mean Std. Dev. Min Max -------------+-------------------------------------------------------- e2 | 49 1177.546 1529.095 .0054078 6581.732generate c = sqrt(s2/r(mean)) table region, contents(freq mean c)---------------------------------- Region | Freq. mean(c) ----------+----------------------- 1 | 9 1.177438 2 | 12 1.502558 3 | 16 .475338 4 | 12 .9383478 ----------------------------------/* Part of Table 7.7, page 195 */ regress y x1 x2 x3 [aw=1/c^2](sum of wgt is 9.6249e+01) Source | SS df MS Number of obs = 49 -------------+------------------------------ F( 3, 45) = 47.62 Model | 76012.6369 3 25337.5456 Prob > F = 0.0000 Residual | 23943.4288 45 532.076197 R-squared = 0.7605 -------------+------------------------------ Adj R-squared = 0.7445 Total | 99956.0657 48 2082.41804 Root MSE = 23.067 ------------------------------------------------------------------------------ y | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- x1 | .0624611 .0078028 8.00 0.000 .0467455 .0781767 x2 | .8739911 .1983961 4.41 0.000 .4744008 1.273581 x3 | .0289241 .0339939 0.85 0.399 -.0395432 .0973914 _cons | -316.0237 77.41892 -4.08 0.000 -471.9535 -160.094 ------------------------------------------------------------------------------/* Figure 7.10, page 196 */ /* Note 1: Predicted values and residuals need to be adjusted for by the weights used in the wls.*/ /* Note 2: For this figure and the next, Stata does not compute standardized residuals for weighted data, therefore we are going to use the unstandardized residuals.*/ predict p3 predict r3, residual generate wp = p3*1/c generate wr = r3*1/c graph twoway scatter wr wp, xlabel(250(125)750)
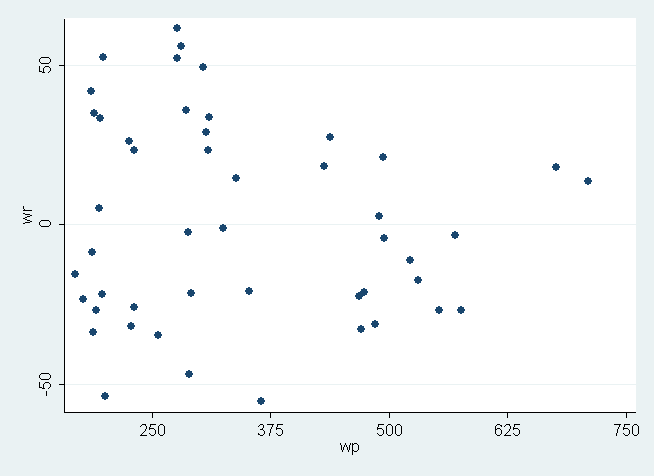
/* Figure 7.11, page 196 */
graph twoway scatter wr region, xlabel(1(1)4)